Fractional-order excitable neural system with bidirectional coupling

Abstract

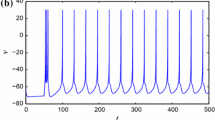
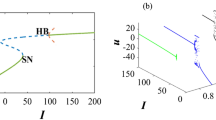
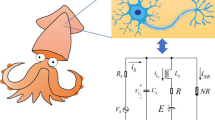
Fractional-order dynamics is applicable to biological excitable systems with strong interactions or systems with long-term memory effect. The activity of neural membrane voltage depends on the long-range correlations of ionic conductances. Such a behavior of the membrane voltage with long-range correlation can be better described with a fractional-order dynamics. A fractional-order coupled modified three-dimensional (3D) Morris–Lecar (M–L) neural system has been presented to show the variations in the firing patterns from resting state $\rightarrow$ oscillatory pattern $\rightarrow$ bursting and the synchronous behavior by designing a bidirectional coupling mechanism. The fractional exponents are lying between 0 and 1. The predominant controller of the changes of firing behavior is the fractional exponent. The stability of synchronization and nature of the fractional system dynamics have been analyzed. To make the investigations more convincing and biologically plausible, we consider a network of M–L oscillators with bidirectional synaptic coupling functions using global type connections and present the effectiveness of the coupling scheme.

Appendix

The numerical computations of nonlinear fractional order systems have various approximation techniques. We use the Caputo fractional derivative and consider the predictor–corrector algorithm technique to solve the fractional order system as well as the coupled system to show the synchronization effect. The scheme is based on the Adams–Bashforth–Moulton method [17, 29, 43]. This is a time domain approximation scheme. We analyze the method as follows. Consider the fractional order system as

$$\begin{aligned} {D^\gamma }x(t) = G(t,\,\,x(t)),\,\,0< \gamma \le 1,\,\,0 < t \le T, \end{aligned}$$

where ${x^{(m)}}(0) = x_0^{(m)},\,\,m = 1,\,\,2,\ldots ,\,\,k - 1.$ The above fractional order system is equivalent to Volterra integral equation

$$\begin{aligned} x(t)= & {} \sum \limits _{m = 0}^{\left\lceil \gamma \right\rceil - 1} {x_0^{(m)}({{{t^m}} \big / m}!} ) + ({1 \big / {\varGamma (\gamma )}})\\&\int \limits _0^t {{{(t - {t_1})}^{\gamma - 1}}G({t_1},x({t_1}))\hbox {d}{t_1}} , \end{aligned}$$

consider $h = T/N,\,\,{t_n} = nh\,\,(n = 0,\,\,1,\,\,2,\ldots ,\,\,N).$ The above integral equation can be solved in the following way

$$\begin{aligned}&{x_h}({t_{n + 1}}) = \sum \limits _{m = 0}^{\left\lceil \gamma \right\rceil - 1} {x_0^{(m)}({t^m}/m!)} + ({{{h^\gamma }} \big / {\varGamma (\gamma + 2)}})\\&G({t_{n + 1}},x_h^r({t_{n + 1}})) + ({{{h^\gamma }} \big / {\varGamma (\gamma + 2)}})\sum \limits _{i = 0}^n {\alpha _{i,n + 1}}\\&\quad G({t_i},{x_h}({t_i})), \end{aligned}$$

where

$$\begin{aligned} {\alpha _{i,n + 1}} = \left\{ {\begin{array}{ll} {{n^{\gamma + 1}} - (n - \gamma ){{(n + 1)}^\gamma },\quad i = 0,}\\ \begin{array}{l} {(n - i + 2)^{\gamma + 1}} + {(n - i)^{\gamma + 1}} \\ - 2{(n - i + 1)^{\gamma + 1}},\quad 1 \le \hbox {i} \le n, \end{array}\\ 1,\quad i = n + 1, \end{array}} \right. \end{aligned}$$

and ${\beta _{i,n + 1}} = ({{{h^\gamma }} / \gamma })({(n + 1 - i)^\gamma } - {(n - i)^\gamma }),$ then the discretized function becomes $x_h^\gamma ({t_{n + 1}}) = \sum \nolimits _{m = 0}^{\left\lceil \gamma \right\rceil - 1} {x_0^{(m)}({{{t^m}} / {m!}})} + ({1 / {\varGamma (\gamma )}})\sum \nolimits _{i = 0}^n {\beta _{i,n + 1}}G({t_i},{x_h}({t_i})).$ The error dynamics function of the above approximation is expressed as follows: $\max \nolimits _{i = 1,\,\,2,\ldots ,\,\,N} \left| {x({t_i}) - {x_h}({t_i})} \right| = O({h^r}),$ where $r = \min (2,\,\,1 + \gamma ).$ Using the above mentioned procedure, the nonlinear system of initial value fractional order system can be discretized and solved numerically.