Dynamics of a middle ear with fractional type of dissipation

Abstract

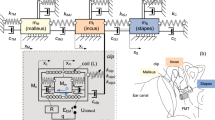
In this paper, a model of spatial motion of the ossicular chain described as a system of two rigid bodies connected to the temporal bone through the system of particularly chosen massless viscoelastic rods was proposed. Several assumptions regarding the relative motion between incus and malleus, external loading force, distributed pressure of the perilymph on the stapes baseplate behind the oval window, and supporting ligaments were made. In order to avoid merging with fractional partial differential equations, the dissipation of energy due to the deformation of the eardrum is taken into account through deformation of its radial fibers while simple shear deformation pattern of the stapedial annular ligament was replaced by uniaxial deformation of viscoelastic rods. By use of the Gibbs–Appel approach and the complementary constitutive axioms corresponding to the fractional Kelvin–Zener model of viscoelastic body, the equations of motion were derived. The Cauchy problem given in terms of coupled fractional differential equations was transformed in the equivalent integer order form and solved numerically by standard numerical procedures. These results, obtained by means of the Atanackovic–Stankovic expansion formula, were compared with the ones received by use of Laplace’s transform and its numerical inversion. As a principal novelty, this model uses both fractional calculus and recently reported results on mechanical tests performed on human middle ear tissues. Thus, it can be used for either predicting of the middle ear behavior in normal and pathological conditions or simulations preceding implants design within restoration of the hearing function.

Appendix

In order to illustrate how the proposed model works practically, the references describing ossicular chain and the tissues included in its suspension system were examined, and the values of inertial, rheological, and geometrical parameters were selected as follows.

The inertial properties of stapes and IMB listed in Table 1 were taken from [52]. The positions of characteristic points of the stapes and IMB, determined on the basis of their orthogonal projections given in Figs. 4 and 5 of reference [52], are shown in Tables 2 and 3, respectively.

Table 1 Inertial properties of the rigid bodies, taken from [52]

Table 2 Positions of the stapes characteristic points determined from [52]

Table 3 Positions of IMB characteristic points determined from [52]

From the same paper, one can obtain the orthogonal matrices describing the orientations of the coordinate systems $C_{1}x_{1}y_{1}z_{1}$ and $C_{2}x_{2}y_{2}z_{2},$ with respect to the inertial one, in our notation

$$\begin{aligned}&\mathbf {K}_{1}= \begin{pmatrix} 0.9920 &{} -0.1257 &{} -0.0113 \\ 0.1258 &{} 0.9920 &{} 0.0113 \\ 0.0098 &{} -0.0127 &{} 0.9998 \end{pmatrix},\\&\mathbf {K}_{2}= \begin{pmatrix} 0.9033 &{} -0.2410 &{} -0.3549 \\ 0.2129 &{} 0.9700 &{} -0.1170 \\ 0.3725 &{} 0.0301 &{} 0.9275 \end{pmatrix}. \end{aligned}$$

Positions on IMB to which the viscoelastic rods are connected was taken from [43]. The radius vectors of these points are listed in Table 4.

Table 4 Positions of the characteristic points on IMB to which the viscoelastic rods are connected, taken from [43]

The unit vectors describing the directions of the forces acting on stapes, $\varvec{\kappa }_{1k}= \begin{bmatrix} 1&0&0 \end{bmatrix} ^\mathrm{{T}},$ $k=1\div 4,$ and $\varvec{\kappa }_{15}= \begin{bmatrix} 0&1&0 \end{bmatrix} ^\mathrm{{T}},$ were obtained from the anatomy of the middle ear, see [6]. The ones describing the directions of the ligaments connected to IMB are determined from [43] and shown in Table 5.

Table 5 Unit vectors of IMB ligaments determined from [43]

The unit vectors corresponding to the eardrum radial fibers used and the direction of loading force are determined using Fig. 5 of [14] and are listed in Table 6.

Table 6 Unit vectors of the forces related to two functions of the eardrum, determined from [14]

Assuming the constant thickness of the stapedial annular ligament, the initial length and cross-sectional area of the rods used instead were taken from [19], and are $l_{1k}=0.07$ mm and $A_{1k}=0.4378$ mm$^{2},$ $k=1\div 4.$, respectively. The initial length and cross-sectional area of the rod used instead of the tendon of stapedial muscle were taken from [10] and read $l_{1k}=0.99$ mm and $A_{1k}=0.156$ mm$^{2},$ respectively.

The initial lengths and cross-sectional areas of the rods substituting for the ligaments of IMB were taken from [43] and are listed in Table 7.

Table 7 Initial lengths and cross-sectional areas of the rods substituting for the ligaments of IMB, taken from [43]

The initial lengths of the viscoelastic rods that will take the eardrum energy dissipation were $l_{26}=3.668$ mm, $l_{27}=3.2$ mm and $l_{28}=4.452$ mm, while the area of their cross sections is assumed to be the same $A_{2i}=1$ mm$^{2}$, $i=6\div 8.$

The biorheological parameters of the fractional Kelvin–Zener model describing soft tissues of the middle ear are taken from [13] and shown in Tables 8 and 9. Following the same procedure as described therein, the rheological parameters of the annular ligament of the stapes were determined on the basis of experimental results presented in [19]. These parameters are also shown in Table 8 and denoted by $^{*}$.

Table 8 Stapes rheological parameters of the fractional Kelvin–Zener model, taken from [13]

Table 9 IMB rheological parameters of the fractional Kelvin–Zener model, taken from [13]

The parameters of the total force and the total moment used to estimate the distributed pressure of perilymph on the stapes baseplate are, respectively, $k_{1}=0.2$ Ns/m and $k_{2}=1\mathbf \,{\times }\,10^{-6}$ Nms. The value of $k_{1}$ was taken from [18]. The value of $k_{2}$ is taken to be very small due to the dimensions of the stapes baseplate and because the rotation of stapes baseplate causes very small changes in net volume of perilymph in the inner ear.

Finally, matrices $\mathbf {M}_{1},~\mathbf {M}_{2},~\mathbf {M}_{3}$, and vector $\mathbf {V}_{1}$ in system of Eq. (12) are as follows.

The elements of symmetric matrix $\mathbf {M}_{1}=\left[ m_{ij}^{1}\right] _{6\times 6},$ read

$$\begin{aligned} m_{11}^{1}= & {} \left( B_{1}+B_{2}\right) , \\ m_{12}^{1}= & {} m_{21}^{1}=\left( B_{1}\nu _{C_{1}}^{O_{1}}+B_{2}\nu _{Z}^{O_{1}}\right) , \\ m_{13}^{1}= & {} m_{31}^{1}=-\left( B_{1}\mu _{C_{1}}^{O_{1}}+B_{2}\mu _{Z}^{O_{1}}\right) , \\ \end{aligned}$$

$$\begin{aligned} m_{14}^{1}= & {} m_{41}^{1}=B_{2}\left( k_{13}^{2}\eta _{C_{2}}^{Z}-k_{12}^{2}\zeta _{C_{2}}^{Z}\right) , \\ m_{15}^{1}= & {} m_{51}^{1}=B_{2}\left( k_{11}^{2}\zeta _{C_{2}}^{Z}-k_{13}^{2}\xi _{C_{2}}^{Z}\right) , \\ m_{16}^{1}= & {} m_{61}^{1}=B_{2}\left( k_{12}^{2}\xi _{C_{2}}^{Z}-k_{11}^{2}\eta _{C_{2}}^{Z}\right) , \end{aligned}$$

$$\begin{aligned} m_{22}^{1}= & {} B_{1}\left( \left( \nu _{C_{1}}^{O_{1}}\right) ^{2}+\left( \lambda _{C_{1}}^{O_{1}}\right) ^{2}\right) \\&+\,\left( k_{21}^{1}\right) ^{2}J_{x_{1}}+\left( k_{22}^{1}\right) ^{2}J_{y_{1}}+\left( k_{23}^{1}\right) ^{2}J_{z_{1}} \\&+\,B_{2}\left( \left( \nu _{Z}^{O_{1}}\right) ^{2}+\left( \lambda _{Z}^{O_{1}}\right) ^{2}\right) , \\ m_{23}^{1}= & {} m_{32}^{1}=k_{21}^{1}k_{31}^{1}J_{x_{1}}+k_{22}^{1}k_{32}^{1}J_{y_{1}}+k_{23}^{1}k_{33}^{1}J_{z_{1}}\\&-B_{1}\mu _{C_{1}}^{O_{1}}\nu _{C_{1}}^{O_{1}} -\,B_{2}\mu _{Z}^{O_{1}}\nu _{Z}^{O_{1}}, \\ m_{24}^{1}= & {} m_{42}^{1}=B_{2}\left( \left( k_{13}^{2}\eta _{C_{2}}^{Z}-k_{12}^{2}\zeta _{C_{2}}^{Z}\right) \nu _{Z}^{O_{1}}\right. \\&\left. +\left( k_{32}^{2}\zeta _{C_{2}}^{Z}-k_{33}^{2}\eta _{C_{2}}^{Z}\right) \lambda _{Z}^{O_{1}}\right) , \\ m_{25}^{1}= & {} m_{52}^{1}=B_{2}\left( \left( k_{11}^{2}\zeta _{C_{2}}^{Z}-k_{13}^{2}\xi _{C_{2}}^{Z}\right) \nu _{Z}^{O_{1}}\right. \\&\left. +\left( k_{33}^{2}\xi _{C_{2}}^{Z}-k_{31}^{2}\zeta _{C_{2}}^{Z}\right) \lambda _{Z}^{O_{1}}\right) , \\ \end{aligned}$$

$$\begin{aligned} m_{26}^{1}= & {} m_{62}^{1}=B_{2}\left( \left( k_{12}^{2}\xi _{C_{2}}^{Z}-k_{11}^{2}\eta _{C_{2}}^{Z}\right) \nu _{Z}^{O_{1}}\right. \\&\left. +\left( k_{31}^{2}\eta _{C_{2}}^{Z}-k_{32}^{2}\xi _{C_{2}}^{Z}\right) \lambda _{Z}^{O_{1}}\right) , \\ m_{33}^{1}= & {} B_{1}\left( \left( \mu _{C_{1}}^{O_{1}}\right) ^{2}+\left( \lambda _{C_{1}}^{O_{1}}\right) ^{2}\right) +\left( k_{31}^{1}\right) ^{2}J_{x_{1}}\\&+\left( k_{32}^{1}\right) ^{2}J_{y_{1}}+\left( k_{33}^{1}\right) ^{2}J_{z_{1}} \\&+\,B_{2}\left( \left( \mu _{Z}^{O_{1}}\right) ^{2}+\left( \lambda _{Z}^{O_{1}}\right) ^{2}\right) , \\ m_{34}^{1}= & {} m_{43}^{1}=B_{2}\left( \left( k_{12}^{2}\zeta _{C_{2}}^{Z}-k_{13}^{2}\eta _{C_{2}}^{Z}\right) \mu _{Z}^{O_{1}}\right. \\&\left. +\left( k_{23}^{2}\eta _{C_{2}}^{Z}-k_{22}^{2}\zeta _{C_{2}}^{Z}\right) \lambda _{Z}^{O_{1}}\right) , \\ m_{35}^{1}= & {} m_{53}^{1}=B_{2}\left( \left( k_{13}^{2}\xi _{C_{2}}^{Z}-k_{11}^{2}\zeta _{C_{2}}^{Z}\right) \mu _{Z}^{O_{1}}\right. \\&\left. +\left( k_{21}^{2}\zeta _{C_{2}}^{Z}-k_{23}^{2}\xi _{C_{2}}^{Z}\right) \lambda _{Z}^{O_{1}}\right) , \\ m_{36}^{1}= & {} m_{63}^{1}=B_{2}\left( \left( k_{11}^{2}\eta _{C_{2}}^{Z}-k_{12}^{2}\xi _{C_{2}}^{Z}\right) \mu _{Z}^{O_{1}}\right. \\&\left. +\left( k_{22}^{2}\xi _{C_{2}}^{Z}-k_{21}^{2}\eta _{C_{2}}^{Z}\right) \lambda _{Z}^{O_{1}}\right) , \end{aligned}$$

$$\begin{aligned} m_{44}^{1}&=B_{2}\left( \left( k_{13}^{2}\eta _{C_{2}}^{Z}-k_{12}^{2}\zeta _{C_{2}}^{Z}\right) ^{2}+\left( k_{23}^{2}\eta _{C_{2}}^{Z}-k_{22}^{2}\zeta _{C_{2}}^{Z}\right) ^{2}\right. \\&\quad \ +\left. \left( k_{33}^{2}\eta _{C_{2}}^{Z}-k_{32}^{2}\zeta _{C_{2}}^{Z}\right) ^{2}\right) + J_{x_{2}}, \\ m_{45}^{1}&=m_{54}^{1}=B_{2}\left( k_{13}^{2}\eta _{C_{2}}^{Z}-k_{12}^{2}\zeta _{C_{2}}^{Z}\right) \left( k_{11}^{2}\zeta _{C_{2}}^{Z}-k_{13}^{2}\xi _{C_{2}}^{Z}\right) \\&\quad \ +B_{2}\left( k_{33}^{2}\eta _{C_{2}}^{Z}-k_{32}^{2}\zeta _{C_{2}}^{Z}\right) \left( k_{31}^{2}\zeta _{C_{2}}^{Z}-k_{33}^{2}\xi _{C_{2}}^{Z}\right) \\&\quad \ +B_{2}\left( k_{23}^{2}\eta _{C_{2}}^{Z}-k_{22}^{2}\zeta _{C_{2}}^{Z}\right) \left( k_{21}^{2}\zeta _{C_{2}}^{Z}-k_{23}^{2}\xi _{C_{2}}^{Z}\right) , \\ m_{46}^{1}&=m_{64}^{1}=B_{2}\left( k_{13}^{2}\eta _{C_{2}}^{Z}-k_{12}^{2}\zeta _{C_{2}}^{Z}\right) \left( k_{12}^{2}\xi _{C_{2}}^{Z}-k_{11}^{2}\eta _{C_{2}}^{Z}\right) \\&\quad \ +B_{2}\left( k_{33}^{2}\eta _{C_{2}}^{Z}-k_{32}^{2}\zeta _{C_{2}}^{Z}\right) \left( k_{32}^{2}\xi _{C_{2}}^{Z}-k_{31}^{2}\eta _{C_{2}}^{Z}\right) \\&\quad \ +B_{2}\left( k_{23}^{2}\eta _{C_{2}}^{Z}-k_{22}^{2}\zeta _{C_{2}}^{Z}\right) \left( k_{22}^{2}\xi _{C_{2}}^{Z}-k_{21}^{2}\eta _{C_{2}}^{Z}\right) , \\ m_{55}^{1}&=B_{2}\left( \left( k_{11}^{2}\zeta _{C_{2}}^{Z}-k_{13}^{2}\xi _{C_{2}}^{Z}\right) ^{2}+\left( k_{21}^{2}\zeta _{C_{2}}^{Z}-k_{23}^{2}\xi _{C_{2}}^{Z}\right) ^{2}\right. \\&\quad \ +\left. \left( k_{31}^{2}\zeta _{C_{2}}^{Z}-k_{33}^{2}\xi _{C_{2}}^{Z}\right) ^{2}\right) + J_{y_{2}}, \\ m_{56}^{1}&=B_{2}\left( k_{11}^{2}\zeta _{C_{2}}^{Z}-k_{13}^{2}\xi _{C_{2}}^{Z}\right) \left( k_{12}^{2}\xi _{C_{2}}^{Z}-k_{11}^{2}\eta _{C_{2}}^{Z}\right) \\&\quad \ +B_{2}\left( k_{31}^{2}\zeta _{C_{2}}^{Z}-k_{33}^{2}\xi _{C_{2}}^{Z}\right) \left( k_{32}^{2}\xi _{C_{2}}^{Z}-k_{31}^{2}\eta _{C_{2}}^{Z}\right) \\&\quad \ +B_{2}\left( k_{21}^{2}\zeta _{C_{2}}^{Z}-k_{23}^{2}\xi _{C_{2}}^{Z}\right) \left( k_{22}^{2}\xi _{C_{2}}^{Z}-k_{21}^{2}\eta _{C_{2}}^{Z}\right) , \\ m_{66}^{1}&=B_{2}\left( \left( k_{12}^{2}\xi _{C_{2}}^{Z}-k_{11}^{2}\eta _{C_{2}}^{Z}\right) ^{2}+\left( k_{22}^{2}\xi _{C_{2}}^{Z}-k_{21}^{2}\eta _{C_{2}}^{Z}\right) ^{2}\right. \\&\quad \ +\left. \left( k_{32}^{2}\xi _{C_{2}}^{Z}-k_{31}^{2}\eta _{C_{2}}^{Z}\right) ^{2}\right) + J_{z_{2}}. \end{aligned}$$

The elements of $\mathbf {M}_{2}=\left[ m_{i,j}^{2}\right] _{6\times 13}$ are

$$\begin{aligned}&\displaystyle m_{1,j}^{2}=\kappa _{1jx},~m_{1,i+5}^{2}=\kappa _{2ix},~ \\&\displaystyle m_{2,j}^{2}=\kappa _{1jx}\nu _{1j}^{O_{1}}-\kappa _{1jz}\lambda _{1j}^{O_{1}},\\&m_{2,i+5}^{2}=\kappa _{2ix}\nu _{Z}^{O_{1}}-\kappa _{2iz}\lambda _{Z}^{O_{1}}, \\&\displaystyle m_{3,j}^{2}=\kappa _{1jy}\lambda _{1j}^{O_{1}}-\kappa _{1jx}\mu _{1j}^{O_{1}},~m_{3,i+5}^{2}=\kappa _{2iy}\lambda _{Z}^{O_{1}}-\kappa _{2ix}\mu _{Z}^{O_{1}}, \\&\displaystyle m_{4,j}^{2}=0,\quad m_{5,j}^{2}=0,\quad m_{6,j}^{2}=0, \\ \end{aligned}$$

$$\begin{aligned} \displaystyle m_{4,i+5}^{2}= & {} \kappa _{2ix}\left( k_{13}^{2}\eta _{2i}^{Z}-k_{12}^{2}\zeta _{2i}^{Z}\right) +\kappa _{2iy}\left( k_{23}^{2}\eta _{2i}^{Z}-k_{22}^{2}\zeta _{2i}^{Z}\right) \\&\displaystyle +\,\kappa _{2iz}\left( k_{33}^{2}\eta _{2i}^{Z}-k_{32}^{2}\zeta _{2i}^{Z}\right) , \\ \displaystyle m_{5,i+5}^{2}= & {} \kappa _{2ix}\left( k_{11}^{2}\zeta _{2i}^{Z}-k_{13}^{2}\xi _{2i}^{Z}\right) +\kappa _{2iy}\left( k_{21}^{2}\zeta _{2i}^{Z}-k_{23}^{2}\xi _{2i}^{Z}\right) \\&\displaystyle +\,\kappa _{2iz}\left( k_{31}^{2}\zeta _{2i}^{Z}-k_{33}^{2}\xi _{2i}^{Z}\right) , \\ \displaystyle m_{6,i+5}^{2}= & {} \kappa _{2ix}\left( k_{12}^{2}\xi _{2i}^{Z}-k_{11}^{2}\eta _{2i}^{Z}\right) +\kappa _{2iy}\left( k_{22}^{2}\xi _{2i}^{Z}-k_{21}^{2}\eta _{2i}^{Z}\right) \\&\displaystyle +\,\kappa _{2iz}\left( k_{32}^{2}\xi _{2i}^{Z}-k_{31}^{2}\eta _{2i}^{Z}\right) , \end{aligned}$$

where $j=1\div 5$ and $i=1\div 8$, while nontrivial elements of $\mathbf {M}_{3}=\left[ m_{ij}^{3}\right] _{6\times 6}$ are $m_{11}^{3}=-k_{1},$ $m_{22}^{3}=m_{33}^{3}=-k_{2}.$

Vector $\mathbf {V}_{1}$ reads

$$\begin{aligned} \mathbf {V}_{1}= \left[ \begin{array}{l} \kappa _{29x} \\ \kappa _{29x}\nu _{Z}^{O_{1}}-\kappa _{29z}\lambda _{Z}^{O_{1}} \\ \kappa _{29y}\lambda _{Z}^{O_{1}}-\kappa _{29x}\mu _{Z}^{O_{1}} \\ \kappa _{29x}\left( k_{13}^{2}\eta _{29}^{Z}-k_{12}^{2}\zeta _{29}^{Z}\right) +\kappa _{29y}\left( k_{23}^{2}\eta _{29}^{Z}-k_{22}^{2}\zeta _{2i9}^{Z}\right) \\ \quad +\,\kappa _{29z}\left( k_{33}^{2}\eta _{29}^{Z}-k_{32}^{2}\zeta _{29}^{Z}\right) \\ \kappa _{29x}\left( k_{11}^{2}\zeta _{29}^{Z}-k_{13}^{2}\xi _{29}^{Z}\right) +\kappa _{29y}\left( k_{21}^{2}\zeta _{29}^{Z}-k_{23}^{2}\xi _{29}^{Z}\right) \\ \quad +\,\kappa _{29z}\left( k_{31}^{2}\zeta _{29}^{Z}-k_{33}^{2}\xi _{29}^{Z}\right) \\ \kappa _{29x}\left( k_{12}^{2}\xi _{29}^{Z}-k_{11}^{2}\eta _{29}^{Z}\right) +\kappa _{29y}\left( k_{22}^{2}\xi _{29}^{Z}-k_{21}^{2}\eta _{29}^{Z}\right) \\ \quad +\,\kappa _{29z}\left( k_{32}^{2}\xi _{29}^{Z}-k_{31}^{2}\eta _{29}^{Z}\right) \end{array}\right] . \end{aligned}$$