Abstract
In this paper, bifurcation analysis of a high-speed twin-propeller twin-rudder ship maneuvering mathematical model has been carried out. Surge, sway, yaw, and roll are the degrees of freedom considered in the model. Coupling of roll with sway and yaw motion during zigzag and turning maneuvers is shown. Hopf, fold, and period-doubling-type bifurcations are identified by allowing one-parameter numerical continuation of equilibrium. The vertical center of gravity is considered as the bifurcation parameter. Physical behavior of roll motion and capsize during the bifurcations are discussed. The bifurcation analysis is carried out using MATCONT. MATCONT is an MATLAB-based program that computes curves of equilibrium and its bifurcation points for any dynamical system. Influence of the wind on roll angle during turning maneuver is shown.













Similar content being viewed by others
Abbreviations
- \(a_\mathrm{H} \) :
-
Ratio of additional lateral force induced on ship hull by rudder action to the rudder force
- \({C}'_\mathrm{Rr} \) :
-
Rudder flow-straightening coefficients for yaw rate
- \({C}'_{\mathrm{R}\delta } \) :
-
Rudder flow-straightening coefficients for rudder angle
- \(C_\mathrm{RQa},\) \(C_\mathrm{RQb}\) :
-
Rudder torque coefficients
- \(C_\mathrm{T}\) :
-
Coefficient of total resistance
- \(D_\mathrm{P}\) :
-
Propeller diameter
- Fn :
-
Froude number
- \(f_\alpha \) :
-
Rudder normal force coefficient
- \(F_{x\mathrm{R}} , F_{y\mathrm{R}} \) :
-
Surge and sway forces acting on rudders, in rudder-fixed coordinate system
- \(I_x \) :
-
Moment of inertia of the ship about x-axis
- \(I_z \) :
-
Moment of inertia of the ship about z-axis
- \(I_\mathrm{P} \) :
-
Moment of inertia of the propeller and shaft
- \(J_\mathrm{P} \) :
-
Propeller advance ratio
- \(J_z \) :
-
Added mass moment of inertia of ship with respect to z-axis.
- \(J_x \) :
-
Added mass moment of inertia of ship with respect to x-axis.
- \(K_\mathrm{H} \) :
-
Bare hull hydrodynamic moment in x direction at midship
- \(K_{\dot{v}} , K_{\dot{r}},\) \(N_{\dot{v}} \) and \(N_{\dot{r}} \) :
-
are the added mass moment of inertia
- \(K_\mathrm{R} \) :
-
Hydrodynamic moment acting about x-axis on ship due to twin rudders
- \(K_\mathrm{P} \) :
-
Hydrodynamic moment acting about x-axis on ship due to twin propellers
- \(K_\mathrm{W} \) :
-
Hydrodynamic moment due to wind acting on ship about x-axis
- K :
-
Rudder form factor
- \(K_\mathrm{T} \) :
-
Thrust coefficient
- \(K_\mathrm{Q} \) :
-
Torque coefficient
- L :
-
Ship length
- \(l_1 \) :
-
First Lyapunov coefficient
- m :
-
Mass of the ship
- \(N_\mathrm{H} \) :
-
Bare hull hydrodynamic moment in z direction at midship
- \(N_\mathrm{R} \) :
-
Hydrodynamic moment due to twin rudders acting on ship about z direction
- \(N_\mathrm{P} \) :
-
Hydrodynamic moment due to twin propellers acting on ship about z direction
- \(N_\mathrm{W} \) :
-
Hydrodynamic moment due to wind acting on ship about z direction
- \(n_\mathrm{P} \) :
-
Propeller revolutions
- p :
-
Roll rate of ship about x-axis
- \(Q_\mathrm{E} \) :
-
Engine torque
- \(Q_\mathrm{P} \) :
-
Propeller torque
- \(Q_\mathrm{R} \) :
-
Rudder torque
- r :
-
Yaw rate of ship about z-axis
- \(R_\mathrm{n} \) :
-
Reynolds number
- T :
-
Ship draft
- \(T_\phi \) :
-
Natural period of roll
- \(t_\mathrm{P} \) :
-
Thrust deduction factor
- \(t_\mathrm{R} ,\) and \(x_H \) :
-
are the rudder–hull interaction coefficients
- u :
-
Surge velocity of ship in x direction
- \(u_\mathrm{A} \) :
-
Absolute surge velocity of ship in x direction in wind
- \(U_\mathrm{W} \) :
-
Absolute wind velocity
- v :
-
Sway velocity of ship in y direction
- \(v_\mathrm{A} \) :
-
Absolute sway velocity of ship in y direction in wind
- \(v_\mathrm{R} \) :
-
Sway inflow velocity twin rudders
- \(w_\mathrm{P} \) :
-
Propeller wake fraction
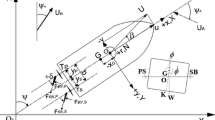
- \((x_\mathrm{G} ,y_\mathrm{G} ,z_\mathrm{G} )\) :
-
Position of center of gravity of ship from the origin O
- \(X_*\) :
-
Resistance of ship in longitudinal direction
- \(X_{\dot{u}}, Y_{\dot{v}},\) \(Y_{\dot{r}}, Y_{\dot{p}} \) :
-
Added mass
- \(X_\mathrm{H} \) :
-
Bare hull hydrodynamic force in x direction at midship
- \(x_\mathrm{lpR} \) :
-
Distance between leading edge to rudder center of pressure
- \(x_\mathrm{lsR} \) :
-
Distance between leading edge to rudder stock
- \(x_\mathrm{spR} \) :
-
Distance between rudder stock to center of pressure
- \(X_\mathrm{P} \) :
-
Hydrodynamic force due to twin propellers acting on ship in x direction
- \(X_\mathrm{R} \) :
-
Hydrodynamic force due to twin rudders acting on ship in x direction
- \(X_\mathrm{W} \) :
-
Hydrodynamic force due to wind acting on ship in x direction
- \(Y_\mathrm{H} \) :
-
Bare hull hydrodynamic force in y direction at midship
- \(Y_\mathrm{R} \) :
-
Hydrodynamic force due to twin rudders acting on ship in y direction
- \(Y_\mathrm{W} \) :
-
Hydrodynamic force due to wind acting on ship in y direction
- \(Y_\mathrm{P} \) :
-
Hydrodynamic force due to twin propellers acting on ship in y direction
- \(y_\mathrm{P} \) :
-
Offset distance of rudder stock from the ship center line
- \(z_\mathrm{H} \) :
-
Vertical distance between the acting point of sway hydrodynamic force on hull and the origin of the body-fixed frame
- \(z_\mathrm{R} \) :
-
Vertical distance between the acting point of lift force on rudder \(Y_R \) and the origin of the body-fixed frame
- \(\alpha _\mathrm{R} \) :
-
Effective rudder inflow angle
- \(\beta \) :
-
Ship drift angle
- \(\beta _\mathrm{P} \) :
-
Geometrical drift angle induced at the propeller position due to ship motions
- \(\beta _\mathrm{R} \) :
-
Geometrical drift angle induced at the rudder position due to ship motions
- \(\gamma _\mathrm{R} \) :
-
Rudder flow-straightening coefficients for drift angle
- \(\delta \) :
-
Rudder angle
- \(\delta _0 \) :
-
Neutral rudder angle for straight motion
- \(\rho \) :
-
Water density
- \(\psi \) :
-
Heading angle of ship
- \(\psi _\mathrm{W} \) :
-
Heading angle of wind
- \(\psi _\mathrm{R} \) :
-
Relative heading angle between wind and ship
- \(\psi _\mathrm{A} \) :
-
Absolute heading angle of ship in wind
- \(\phi \) :
-
Roll angle of ship.
The superscript \((')\) represents the non-dimensional value.
The subscript {S} and {P} denote starboard and port side, respectively.
The time derivative of a variable is denoted by a dot above the variable, e.g., \(\dot{\phi }\) is the time derivative of \(\phi \).
References
Hirano, M., Takashina, J.: A calculation of ship turning motion taking coupling effect due to heel into consideration. Trans. West-Japan Soc. Nav. Archit. 59, 71–81 (1980)
Eda, H.: Maneuvering performance of high-speed ships with effect of roll motion. Ocean Eng. 7(3), 379–397 (1980)
Son, K.H., Nomoto, K.: On the coupled motion of steering and rolling of a high-speed container ship. Nav. Archit. Ocean Eng. 20, 73–83 (1982)
Spyrou, K.: Yaw stability of ships in steady wind. Ship. Technol. Res. 42, 21–30 (1995)
Oh, I.G., Nayfeh, A.: Nonlinearly interacting responses of the two rotational modes of motion—roll and pitch motions. In: 21st Symposium on Naval Hydrodynamics, Trondheim, Norway, June 24–28 (1996)
Falzarano, J., Steindl, A., Troesch, A., Troger, H.: Rolling motion of ships treated as bifurcation problem. In: Bifurcation and Chaos: Analysis, Algorithms, Applications, pp. 117–121. Birkhäuser, Basel (1991)
Francescutto, A., Contento, G.: Bifurcations in ship rolling: experimental results and parameter identification technique. Ocean Eng. 26(11), 1095–1123 (1999)
Umeda, N., Hashimoto, H., Minegaki, S., Matsuda, A.: An investigation of different methods for the prevention of parametric rolling. J. Mar. Sci. Technol. 13(1), 16–23 (2008)
Virgin, L.N.: The nonlinear rolling response of a vessel including chaotic motions leading to capsize in regular seas. Appl. Ocean Res. 9(2), 89–95 (1987)
El-Nagar, A., El-Bassiouny, A.: Harmonic, subharmonic, superharmonic, simultaneous sub/super harmonic and combination resonances of self-excited two coupled second order system to multi-frequency excitations. J. Acta Mech. 8, 61–71 (1993)
Nayfeh, A.H., Balachandran, B.: Applied Non-Linear Mechanics. Wiley/Interscience, New York (1994)
Dhooge, A., Govaerts, W., Kuznetsov, Yu A.: MATCONT: a MATLAB package for numerical bifurcation analysis of ODEs. ACM Trans. Math. Softw. 29(2), 141–164 (2003)
Dhooge, A., et al.: New features of the software MatCont for bifurcation analysis of dynamical systems. Math. Comput. Model. Dyn. Syst. 14(2), 147–175 (2008)
International Maritime Organization: Explanatory notes to the standards for ship manoeuvrability, MSC/ Circ. 1053 (2002)
American Bureau of Shipping: Guide for the assessment of parametric roll resonance in the design on container carriers (2008)
Det Norske Veritas: Rules for high speed, light craft and naval surface craft, Part 1, Chapter 2, Section 2 (1999)
Khanfir, S., Hasegawa, K., Nagarajan, V., Shouji, K., Lee, S.K.: Manoeuvring characteristics of twin-rudder systems: rudder–hull interaction effect on the manoeuvrability of twin-rudder ships. J. Mar. Sci. Technol. 16(4), 472–490 (2011)
Dash, A.K., Nagarajan, V.: A stochastic response surface approach for uncertainty propagation in ship maneuvering. Int. Shipbuild. Progr. 61(3), 29–161 (2014). doi:10.3233/ISP140110
Fujiwara, T., Ueno, M., Nimura, T.: Estimation of wind forces and moments acting on ships. JASNAOE 183, 77–90 (1998)
Nagarajan, V., Kang, D.H., Hasegawa, K., Nabeshima, K.: Comparison of the mariner Schilling rudder and the mariner rudder for VLCCs in strong winds. J. Mar. Sci. Technol. 13(1), 24–39 (2008)
Hallmann, R., Toxopeus, S.L.: Validation and Extension of the Rotating Arm Functionality in the Seakeeping and Manoeuvring Basin. MARIN., Report No. 21569-1-DT/SMB (2007)
Simonsen, C.D.: PMM model test with DDG51 including uncertainty analysis. Project No. ONRII187.01, FORCE Technology, Denmark (2004)
Simman (2008). http://www.simman2008.dk/
Maxsurf software. http://www.bentley.com/en-US/Products/Maxsurf/
Wilson, R.V., Carrica, P.M., Stern, F.: Unsteady RANS method for ship motions with application to roll for a surface combatant. Comput. Fluids 35, 501–526 (2006)
Kuznetsov, I.A.: Elements of Applied Bifurcation Theory, vol. 112. Springer, Berlin (1998)
Larger, L., Goedgebuer, J.P., Erneux, T.: Subcritical Hopf bifurcation in dynamical systems described by a scalar nonlinear delay differential equation. Phys. Rev. E 69(3), 036210 (2004)
National Transportation Safety Board, USA: Aircraft Accident Report, NTSB/AAR-04/04, Page 21 (2001)
Dash, A.K., Nagarajan, V., Sha, O.P.: Uncertainty assessment for ship maneuvering mathematical model. Int. Shipbuild. Progr. (2015). doi:10.3233/ISP-150117
Carrica, P.M., Ismail, F., Hyman, M., Bhushan, S., Stern, F.: Turn and zigzag maneuvers of a surface combatant using a URANS approach with dynamic overset grids. J. Mar. Sci. Technol. 18(2), 166–181 (2013)
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Ship maneuvering mathematical model for TPTR system.
1.1 Hull forces and moments
All hull forces and moments are expressed at midship of hull. The mathematical expression for \(X_H\) is given in Eq. 3, where \(X_*\) represents the resistance of the ship.
The mathematical expression for \(Y_H\) is given in Eq. 4.
The mathematical expression for \(N_H\) is given in Eq. 5.
The mathematical expression for \(K_H\) is given in Eq. 6, where \(K_{\dot{\phi }} \)is the roll damping coefficient, \(mg\overline{GZ}\) is the roll restoring moment, \(z_H\) is the z coordinate of the point (from O) where the lateral hydrodynamic force \(Y_H \) acts and \(Y_H (v,r)\) is the hydrodynamic lateral force acting on the hull and function of v and r(the first six terms in Eq. 4).
1.2 Twin-propeller forces and torque
The mathematical expressions for \(\hbox {X}_P , \hbox {N}_P\) and \(\hbox {Q}_P \) are given in Eq. 7.
The propeller open-water characteristics \(K_T \) and \(K_Q\) are often estimated by propeller open-water test. The thrust deduction \(1-t_P\) and effective wake \(1-w_P \) coefficients are used to express the hull–propeller interactions. These coefficients are influenced by v and r motion parameters of ship.
1.3 Twin-rudder forces and moment
The rudder forces \(X_R ,Y_R ,N_R \) and \(K_R\) may be written as Eq. 9
The coefficients \(a_H\) and \(x_H\) are used to express the hydrodynamic force induced on the hull due to rudder deflection. The normal force acting on the rudder \(F_{RY}\), drag force developed due to rudder \(F_{RX} \) and torque developed due to rudder normal force \(Q_R\) can be expressed as shown in Eq. 10.
The effective inflow velocity \(U_R\) and angle \(\alpha _R\) to the rudder are expressed as shown in Eq. 11.
The longitudinal component of rudder effective flow \(u_R \) can be expressed as Eq. 12. It is greatly influenced by the propeller slipstream. Effective flow at rudder location increases due to the presence of propeller disk ahead of it.
The lateral component of effective flow velocity to rudder \(v_R\) can be expressed as Eq. 13. The value of \(v_R\) is smaller than \(u_R\).
During the maneuvering motion, the windward (outward) side rudder blocks the flow to the leeward (inward) side rudder. Therefore, both rudders get different flow patterns. Thus, the rudder normal forces of both rudders are different in magnitude. This type of asymmetry is also seen in the propeller wake and thrust deduction factor. Validation of the twin-propeller wake and twin-rudder normal force model is shown in [29]. The rudder sway flow model is made discontinuous at \(\delta = 20^{\circ }\) for leeward rudder. Because after \(\delta = 20^{\circ }\), magnitude of the rudder normal force does not follow the conventional pattern.
1.4 Forces and moments due to wind
The wind forces and moment acting on the vessel are estimated as shown in Eq. 15 [19].
To convert the effective wind angle from our coordinate system to Fujiwara’s coordinate system, we use Eq. 16.
Validation of \(20^{\circ }\) zigzag simulation in full scale with free run model test from Carrica et al. [30]
Validation of \(35^{\circ }\) port turning simulation in full scale with free run model test from Carrica et al. [30]
The values of \(C_X ,C_Y ,C_N \) and \(C_K \) are given in Fig. 14. The simulation results of \(20^{\circ }\) zigzag and \(35^{\circ }\) turning maneuvers at \(Fn= 0.413\), GM = 1.966 m are shown in Figs. 15 and 16. The simulation results match well with Carrica et al. [30].
Rights and permissions
About this article
Cite this article
Dash, A.K., Nagarajan, V. & Sha, O.P. Bifurcation analysis of a high-speed twin-propeller twin-rudder ship maneuvering model in roll-coupling motion. Nonlinear Dyn 83, 2035–2053 (2016). https://doi.org/10.1007/s11071-015-2463-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-015-2463-9