Stochastic stability of quasi-partially integrable and non-resonant Hamiltonian systems under parametric excitations of combined Gaussian and Poisson white noises

Abstract

The asymptotic Lyapunov stability with probability one of multi-degree-of freedom quasi-partially integrable and non-resonant Hamiltonian systems subject to parametric excitations of combined Gaussian and Poisson white noises is studied. First, the averaged stochastic differential equations for quasi partially integrable and non-resonant Hamiltonian systems subject to parametric excitations of combined Gaussian and Poisson white noises are derived by means of the stochastic averaging method and the stochastic jump-diffusion chain rule. Then, the expression of the largest Lyapunov exponent of the averaged system is obtained by using a procedure similar to that due to Khasminskii and the properties of stochastic integro-differential equations. Finally, the stochastic stability of the original quasi-partially integrable and non-resonant Hamiltonian systems is determined approximately by using the largest Lyapunov exponent. An example is worked out in detail to illustrate the application of the proposed method. The good agreement between the analytical results and those from digital simulation show that the proposed method is effective.

Appendices

Appendix 1

The SDEs for system (33)are:

$$\begin{aligned}&{\text {d}}{Q_1} = \frac{{\partial H}}{{\partial {P_1}}}{\text {d}}t ,\nonumber \\&{\text {d}}{P_1} = \Big ( - \frac{{\partial H}}{{\partial {Q_1}}} - {\beta _{11}}{P_1} - {\beta _{12}}{P_2} - {\beta _{13}}{P_3} \Big ){\text {d}}t \nonumber \\&\quad + {f_{11}}{P_1}{\text {d}}{B_1}(t) + {f_{12}}{P_2}{\text {d}}{B_2}(t) + {f_{13}}{P_3}{\text {d}}{B_3}(t) \nonumber \\&\quad + {g_{11}}{P_1}{\text {d}}{C_1}(t) + {g_{12}}{P_2}{\text {d}}{C_2}(t)\nonumber \\&\quad + {g_{13}}{P_3}{\text {d}}{C_3}(t) + \frac{1}{2}g_{11}^2{P_1}{[{\text {d}}{C_1}(t)]^2} \nonumber \\&\quad + \frac{1}{2}{g_{12}}{g_{22}}{P_2}{[{\text {d}}{C_2}(t)]^2} + \frac{1}{2}{g_{13}}{g_{33}}{P_3}{[{\text {d}}{C_3}(t)]^2} \nonumber \\&\quad +\ \frac{1}{6}g_{11}^3{P_1}{[{\text {d}}{C_1}(t)]^3} + \frac{1}{6}{g_{12}}g_{22}^2{P_2}{[{\text {d}}{C_2}(t)]^3} \nonumber \\&\quad + \frac{1}{6}{g_{13}}g_{33}^2{P_3}{[{\text {d}}{C_3}(t)]^3} + \frac{1}{{24}}g_{11}^4{P_1}{[{\text {d}}{C_1}(t)]^4} \nonumber \\&\quad + \frac{1}{{24}}{g_{12}}g_{22}^3{P_2}{[{\text {d}}{C_2}(t)]^4} \!+\! \frac{1}{{24}}{g_{13}}g_{33}^3{P_3}{[{\text {d}}{C_3}(t)]^4} \!+\! \cdots ,\nonumber \\&{\text {d}}{Q_2} = \frac{{\partial H}}{{\partial {P_2}}}{\text {d}}t, \nonumber \\&{\text {d}}{P_2} =\Big ( - \frac{{\partial H}}{{\partial {Q_2}}} - {\beta _{21}}{P_1} - {\beta _{22}}{P_2} - {\beta _{23}}{P_3}\Big ){\text {d}}t \nonumber \\&\quad + {f_{21}}{P_1}{\text {d}}{B_1}(t) + {f_{22}}{P_2}{\text {d}}{B_2}(t) + {f_{23}}{P_3}{\text {d}}{B_3}(t) \nonumber \\&\quad + {g_{21}}{P_1}{\text {d}}{C_1}(t) + {g_{22}}{P_2}{\text {d}}{C_2}(t) + {g_{23}}{P_3}{\text {d}}{C_3}(t)\nonumber \\&\quad + \frac{1}{2}{g_{21}}{g_{11}}{P_1}{[{\text {d}}{C_1}(t)]^2}+ \frac{1}{2}g_{22}^2{P_2}{[{\text {d}}{C_2}(t)]^2}\nonumber \\&\quad + \frac{1}{2}{g_{23}}{g_{33}}{P_3}{[{\text {d}}{C_3}(t)]^2} \nonumber \\&\quad + \frac{1}{6}{g_{21}}g_{11}^2{P_1}{[{\text {d}}{C_1}(t)]^3} + \frac{1}{6}g_{22}^3{P_2}{[{\text {d}}{C_2}(t)]^3} \nonumber \\&\quad + \frac{1}{6}{g_{23}}g_{33}^2{P_3}{[{\text {d}}{C_3}(t)]^3} + \frac{1}{{24}}{g_{21}}g_{11}^3{P_1}{[{\text {d}}{C_1}(t)]^4} \nonumber \\&\quad + \frac{1}{{24}}g_{22}^4{P_2}{[{\text {d}}{C_2}(t)]^4} + \frac{1}{{24}}{g_{23}}g_{33}^3{P_3}{[{\text {d}}{C_3}(t)]^4} + \cdots , \nonumber \\&{\text {d}}{Q_3} = \frac{{\partial H}}{{\partial {P_3}}}{\text {d}}t,\nonumber \\&{\text {d}}{P_3} = \Big ( - \frac{{\partial H}}{{\partial {Q_3}}} - {\beta _{31}}{P_1} - {\beta _{32}}{P_2} - {\beta _{33}}{P_3}\Big ){\text {d}}t \nonumber \\&\quad + {f_{31}}{P_1}{\text {d}}{B_1}(t) + {f_{32}}{P_2}{\text {d}}{B_2}(t) + {f_{33}}{P_3}{\text {d}}{B_3}(t) \nonumber \\&\quad + {g_{31}}{P_1}{\text {d}}{C_1}(t) + {g_{32}}{P_2}{\text {d}}{C_2}(t) \nonumber \\&\quad + {g_{33}}{P_3}{\text {d}}{C_3}(t) + \frac{1}{2}{g_{31}}{g_{11}}{P_1}{[{\text {d}}{C_1}(t)]^2} \nonumber \\&\quad + \frac{1}{2}{g_{32}}{g_{22}}{P_2}{[{\text {d}}{C_2}(t)]^2} + \frac{1}{2}g_{33}^2{P_3}{[{\text {d}}{C_3}(t)]^2} \nonumber \\&\quad + \frac{1}{6}{g_{31}}g_{11}^2{P_1}{[{\text {d}}{C_1}(t)]^3} + \frac{1}{6}{g_{32}}g_{22}^2{P_2}{[{\text {d}}{C_2}(t)]^3} \nonumber \\&\quad + \frac{1}{6}g_{33}^3{P_3}{[{\text {d}}{C_3}(t)]^3} + \frac{1}{{24}}{g_{31}}g_{11}^3{P_1}{[{\text {d}}{C_1}(t)]^4} \nonumber \\&\quad + \frac{1}{{24}}{g_{32}}g_{22}^3{P_2}{[{\text {d}}{C_2}(t)]^4} \!+\! \frac{1}{{24}}g_{33}^4{P_3}{[{\text {d}}{C_3}(t)]^4} \!+\! \cdots . \end{aligned}$$

(48)

Appendix 2

The other coefficients of Eqs. (36) and (37) are:

$$\begin{aligned}&{a_{11}} = f_{11}^2{D_1} - {\beta _{11}} + g_{11}^2{\lambda _1}E[Y_1^2] + \frac{1}{3}g_{11}^4{\lambda _1}E[Y_1^4], \nonumber \\&{a_{12}} = [f_{12}^2{D_2} + f_{13}^2{D_3} + \frac{1}{2}g_{12}^2{\lambda _2}E[Y_2^2] \nonumber \\&\quad + \frac{1}{2}g_{13}^2{\lambda _3}E[Y_3^2] \nonumber \\&\quad + \frac{7}{{24}}(g_{12}^2g_{22}^2{\lambda _2}E[Y_2^4] + g_{13}^2g_{33}^2{\lambda _3}E[Y_3^4])]\frac{\gamma }{{1 + \gamma }}, \nonumber \\&{a_{21}} = (f_{21}^2 + f_{31}^2){D_1} + \frac{1}{2}(g_{21}^2 + g_{31}^2){\lambda _1}E[Y_1^2]\nonumber \\&\quad + \frac{7}{{24}}(g_{21}^2g_{11}^2 + g_{31}^2g_{11}^2){\lambda _1}E[Y_1^4] , \nonumber \\&{a_{22}} = [(f_{22}^2 + f_{32}^2){D_2} + (f_{23}^2 + f_{33}^2){D_3} - {\beta _{22}} - {\beta _{33}} \nonumber \\&\quad + \left( g_{22}^2 + \frac{1}{2}g_{32}^2\right) {\lambda _2}E[Y_2^2] + \left( g_{33}^2 + \frac{1}{2}g_{23}^2\right) {\lambda _3}E[Y_3^2] \nonumber \\&\quad +\left( \frac{1}{3}g_{22}^4 + \frac{1}{{12\pi }}{g_{32}}g_{23}^3 + \frac{7}{{24}}g_{22}^2g_{32}^2\right) {\lambda _2}E[Y_2^4]\nonumber \\&\quad + \left( \frac{1}{3}g_{33}^4 + \frac{1}{{12\pi }}{g_{23}}g_{33}^3 + \frac{7}{{24}}g_{23}^2g_{33}^2\right) {\lambda _3}E[Y_3^4]]\frac{\gamma }{{1 + \gamma }}, \nonumber \\&{b_{11}} = 3f_{11}^2D_1 , \nonumber \\&{b_{12}} = 2(f_{12}^2{D_2} + f_{13}^2{D_3})\frac{\gamma }{{1 + \gamma }} , \nonumber \\&{b_{21}} = 2(f_{21}^2 + f_{31}^2){D_1}\frac{\gamma }{{1 + \gamma }}, \nonumber \\&{b_{22}} = [3(f_{22}^2{D_2} + f_{33}^2{D_3}) + f_{32}^2{D_2} + f_{23}^2{D_3}]\nonumber \\&\qquad \quad \times \frac{{2{\gamma ^2}}}{{(1 + \gamma )(1 + 2\gamma )}},\nonumber \\&\varepsilon {V_{111}} = {\left( \frac{{35{\lambda _1}E[Y_1^4]}}{{8{M_{14}}}}\right) ^{\frac{1}{4}}}{g_{11}}{H_1} \nonumber \\&\varepsilon {V_{121}} = - {\left( \frac{{{M_{13}}}}{{{M_{23}}}}\right) ^{\frac{1}{3}}}\varepsilon {V_{111}} \nonumber \\&{\varepsilon ^2}{V_{122}} = \frac{{5g_{11}^4{\lambda _1}E[Y_1^4]}}{{2{M_{23}}{{(\varepsilon {V_{121}})}^2}}}H_1^3 \nonumber \\&\varepsilon {V_{131}} = \Big \{ \frac{1}{{{M_{32}}}}\Big [\frac{3}{2}g_{11}^2{\lambda _1}E[Y_1^2]H_1^2 - {(\varepsilon {V_{111}})^2}{M_{12}} \nonumber \\&\qquad \qquad - {(\varepsilon {V_{121}})^2}{M_{22}}\Big ]\Big \} ^{\frac{1}{2}} \nonumber \\&{\varepsilon ^2}{V_{132}} = - \frac{{(\varepsilon {V_{121}})({\varepsilon ^2}{V_{122}}){M_{22}}}}{{(\varepsilon {V_{131}}){M_{32}}}} \nonumber \\&{\varepsilon ^3}{V_{133}} = \frac{{\frac{7}{2}g_{11}^4{\lambda _1}E[Y_1^4]H_1^2 - {{({\varepsilon ^2}{V_{122}})}^2}{M_{22}} - {{({\varepsilon ^2}{V_{132}})}^2}{M_{32}}}}{{2{M_{32}}(\varepsilon {V_{131}})}} \nonumber \\&\varepsilon {V_{211}} = \frac{{\gamma {H_2}}}{{{{\left[ {(1 + \gamma )(1 + 2\gamma )(1 + 3\gamma )(1 + 4\gamma ){M_{14}}} \right] }^{\frac{1}{4}}}}} \nonumber \\&\quad \times {\{ {(105g_{22}^4 \!+\! 9g_{32}^4){\lambda _2}E[Y_2^4] + \left( 105g_{33}^4 + 9g_{23}^4\right) {\lambda _3}E[Y_3^4]} \}^{\frac{1}{4}}}\nonumber \\&\varepsilon {V_{221}} = - {\left( \frac{{{M_{13}}}}{{{M_{23}}}}\right) ^{\frac{1}{3}}}\varepsilon {V_{211}} \nonumber \\&{\varepsilon ^2}{V_{222}} = \frac{{{\gamma ^3}H_2^3}}{{(1 + \gamma )(1 + 2\gamma )(1 + 3\gamma ){M_{23}}{{(\varepsilon {V_{221}})}^2}}} \nonumber \\&\quad \times \Big \{ [15(2g_{22}^4 + g_{22}^2g_{32}^2) + 3(g_{32}^4 + 4g_{22}^2g_{32}^2) \nonumber \\&\quad + \frac{{16}}{\pi }(2{g_{22}}g_{32}^3 + 5g_{22}^3{g_{32}} + \frac{1}{2}g_{32}^3{g_{22}})]{\lambda _2}E[Y_2^4] \nonumber \\&\quad + [15(2g_{33}^4 + g_{23}^2g_{33}^2) + 3(g_{23}^4 + 4g_{23}^2g_{33}^2) \nonumber \\&\quad + \frac{{16}}{\pi }(2{g_{33}}g_{23}^3 + 5g_{33}^3{g_{23}} + \frac{1}{2}g_{23}^3{g_{33}})]{\lambda _3}E[Y_3^4]\Big \} \nonumber \\&\varepsilon {V_{231}} =\Big \{ \frac{1}{{{M_{32}}}}[(3g_{22}^2 + g_{32}^2 + \frac{8}{\pi }{g_{22}}{g_{32}}){\lambda _2}E[Y_2^2] + (g_{23}^2 \nonumber \\& + 3g_{33}^2 + \frac{8}{\pi }{g_{23}}{g_{33}}){\lambda _3}E[Y_3^2]]\frac{{{\gamma ^2}}}{{(1 + \gamma )(1 + 2\gamma )}}H_2^2 \nonumber \\& - {(\varepsilon {V_{211}})^2}{M_{12}} - {(\varepsilon {V_{221}})^2}{M_{22}}]{\Big \} ^{\frac{1}{2}}}\nonumber \\&{\varepsilon ^2}{V_{232}} = - \frac{{(\varepsilon {V_{221}})({\varepsilon ^2}{V_{222}}){M_{22}}}}{{(\varepsilon {V_{231}}){M_{32}}}} \nonumber \\&{\varepsilon ^3}{V_{233}} = \frac{1}{{2{M_{32}}(\varepsilon {V_{231}})}}\Big \{ [(7g_{22}^4 + \frac{{79}}{{12}}g_{22}^2g_{32}^2 + \frac{3}{4}g_{32}^4 \nonumber \\&\quad + \frac{{32}}{{3\pi }}g_{22}^3{g_{32}} + \frac{6}{\pi }g_{32}^3{g_{22}}){\lambda _2}E[Y_2^4] + (7g_{33}^4 \nonumber \\&\quad + \frac{{79}}{{12}}g_{23}^2g_{33}^2 + \frac{3}{4}g_{23}^4 + \frac{{32}}{{3\pi }}g_{33}^3{g_{23}} + \frac{6}{\pi }g_{23}^3{g_{33}}) \nonumber \\&\quad \times {\lambda _3}E[Y_3^4]]\frac{{{\gamma ^2}}}{{(1 + \gamma )(1 + 2\gamma )}}H_2^2 \nonumber \\&\quad - {({\varepsilon ^2}{V_{222}})^2}{M_{22}} - {({\varepsilon ^2}{V_{232}})^2}{M_{32}}\Big \}. \end{aligned}$$

(49)

Appendix 3

The other coefficients of Eq. (47) are:

$$\begin{aligned}&{L_{\delta 1}} = - \frac{{E[{{(\varepsilon {{V'}_{\delta 11}}(0){\alpha _\delta })}^2}]}}{2}{M_{12}}\nonumber \\&\qquad + \frac{{E[{{(\varepsilon {{V'}_{\delta 11}}(0){\alpha _\delta })}^3}]}}{3}{M_{13}} \nonumber \\&\qquad - \frac{{E[{{(\varepsilon {{V'}_{\delta 11}}(0){\alpha _\delta })}^4}]}}{4}{M_{14}} \nonumber \\&\quad = - \frac{{\int \nolimits _0^1 {{{[\varepsilon {{V'}_{\delta 11}}(0){\alpha _\delta }]}^2}p({\alpha _1}){\text {d}}{\alpha _1}} }}{2}{M_{12}} \nonumber \\&\qquad + \frac{{\int \nolimits _0^1 {{{[\varepsilon {{V'}_{\delta 11}}(0){\alpha _\delta }]}^3}p({\alpha _1}){\text {d}}\alpha _1 } }}{3}{M_{13}} \nonumber \\&\qquad - \frac{{\int \nolimits _0^1 {{{[\varepsilon {{V'}_{\delta 11}}(0){\alpha _\delta }]}^4}p({\alpha _1}){\text {d}}{\alpha _1}} }}{4}{M_{14}} \nonumber \\&{L_{\delta 2}} = - \frac{{E[{{((\varepsilon {{V'}_{\delta 21}}(0) + {\varepsilon ^2}{{V'}_{\delta 22}}(0)){\alpha _\delta })}^2}]}}{2}{M_{22}} \nonumber \\&\qquad + \frac{{E[{{((\varepsilon {{V'}_{\delta 21}}(0) + {\varepsilon ^2}{{V'}_{\delta 22}}(0)){\alpha _\delta })}^3}]}}{3}{M_{23}} \nonumber \\&\quad = - \frac{{\int \nolimits _0^1 {{{\{ [\varepsilon {{V'}_{\delta 21}}(0) + {\varepsilon ^2}{{V'}_{\delta 22}}(0)]{\alpha _\delta }\} }^2}} p({\alpha _1}){\text {d}}{\alpha _1}}}{2}{M_{22}} \nonumber \\&\qquad + \frac{{\int \nolimits _0^1 {{{\{ [\varepsilon {{V'}_{\delta 21}}(0) + {\varepsilon ^2}{{V'}_{\delta 22}}(0)]{\alpha _\delta }\} }^3}p({\alpha _1}} ){\text {d}}{\alpha _1}}}{3}{M_{23}} \nonumber \\&{L_{\delta 3}} = - \frac{{E[{{( (\varepsilon {{V'}_{\delta 31}}(0) + {\varepsilon ^2}{{V'}_{\delta 32}}(0) + {\varepsilon ^3}{{V'}_{\delta 33}}(0)){\alpha _\delta })}^2}]}}{2}{M_{32}} \nonumber \\&\quad = - \frac{{{M_{32}}}}{2} \int \limits _0^1 {{{\{ \left[ \varepsilon {{V'}_{\delta 31}}(0) + {\varepsilon ^2}{{V'}_{\delta 32}}(0) + {\varepsilon ^3}{{V'}_{\delta 33}}(0)\right] {\alpha _\delta }\} }^2}} \nonumber \\&\qquad \times p({\alpha _1} ){\text {d}}{\alpha _1}. \end{aligned}$$

(50)

Appendix 4

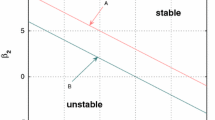
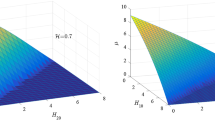
In Figs. 2, 3 and 4, the simulation results for stability domain boundary presented by points are obtained as follows. First, draw the theoretical boundary in plane $(\beta _{11}, \beta _{22}+\beta _{33})$ using Eq. (47) with the given parameters. Then, for every $\beta _{11}$, take one value of $\beta _{22}+\beta _{33}$ near the theoretical boundary, and solve Eq. (33) with small initial system state near trivial solution using the fourth-order Runger–Kutta method. After long time, if system state approaches to trivial solution, then the point $(\beta _{11}, \beta _{22}+\beta _{33})$ is in stable domain. Otherwise, it is in unstable domain. The procedure of this digital simulation please see Appendix B of [21]. It has been described in [21] in detail.