Dynamic analysis of a tethered satellite system with a moving mass

Abstract

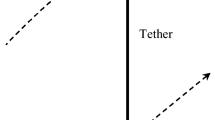
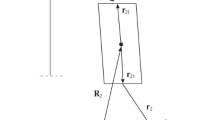
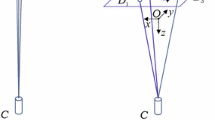
This paper presents a dynamic analysis of a tethered satellite system with a moving mass. A dynamic model with four degrees of freedom, i.e., a two-piece dumbbell model, is established for tethered satellites conveying a mass between them along the tether length. This model includes two satellites and a moving mass, treated as particles in a single orbital plane, which are connected by massless, straight tethers. The equations of motion are derived by using Lagrange’s equations. From the equations of motion, the dynamic response of the system when the moving mass travels along the tether connecting the two satellites is computed and analyzed. We investigate the global tendencies of the libration angle difference (between the two sections of tether) with respect to the changes in the system parameters, such as the initial libration angle, size (i.e. mass) of the moving mass, velocity of the moving mass, and tether length. We also present an elliptic orbit case and show that the libration angles and their difference increase as orbital eccentricity increases. Finally, our results show that a one-piece dumbbell model is qualitatively valid for studying the system under certain conditions, such as when the initial libration angles, moving mass velocity, and moving mass size are small, the tether length is large, and the mass ratio of the two satellites is large.

Appendix

The mass matrix of (17) is a 4×4 matrix given by

$$ \mathbf{M} = [m_{ij}]\quad \mbox{for }i,\quad j = 1, 2, 3, 4 $$

(29)

where

$$\begin{aligned} &{m_{11} = m_{1} + m_{2} + m,} \\ &{m_{12} = m_{21} = - (m_{2} + m)L_{1}\sin \theta_{1} - m_{2}L_{2}\sin \theta_{2},} \\ &{m_{13} = m_{31} = - (m_{2} + m)L_{1} \sin \theta_{1},} \\ &{ m_{14} = m_{41} = - m_{2}L_{2}\sin \theta_{2},} \\ &{ \begin{aligned} m_{22} &= (m_{1} + m_{2} + m)r^{2} \\ &\quad+ (m_{2} + m)L_{1}(L_{1} + 2r\cos \theta_{1}) \\ &\quad+ m_{2}L_{2}\bigl[L_{2} + 2r \cos \theta_{2} + 2L_{1}\cos (\theta_{2} - \theta_{1})\bigr], \end{aligned}} \\ &{ \begin{aligned}[t] m_{23} &= m_{32} \\ &= (m_{2} + m)L_{1}(L_{1} + r\cos \theta_{1}) \\ &\quad+ m_{2}L_{1}L_{2} \cos (\theta_{2} - \theta_{1}), \end{aligned}} \\ &{ \begin{aligned} m_{24} & = m_{42}\\ & = m_{2}L_{2} \bigl[L_{2} + r\cos \theta_{2} + L_{1}\cos ( \theta_{2} - \theta_{1})\bigr], \end{aligned}} \\ &{m_{33} = (m_{2} + m)L_{1}^{2},} \\ &{m_{34} = m_{43} = m_{2}L_{1}L_{2} \cos (\theta_{2} - \theta_{1}), } \\ &{m_{44} = m_{2}L_{2}^{2}} \end{aligned}$$

(30)

The nonlinear internal force vector of (17) is a 4×1 column vector given by

$$ \mathbf{N} = \{ N_{i} \}^{\mathrm{T}}\quad \mbox{for }i = 1, 2, 3, 4 $$

(31)

where

$$\begin{aligned} &{ \begin{aligned}[b] N_{1} &= - (m_{1} + m_{2} + m)r\dot{ \psi}^{2} \\ &\quad- (m_{2} + m) \bigl\{ \bigl[ - \dot{V} + L_{1}(\dot{\psi} + \dot{\theta}_{1})^{2}\bigr] \cos \theta_{1} \\ &\quad+ 2V(\dot{\psi} + \dot{\theta}_{1})\sin \theta_{1} \bigr\} \\ &\quad - m_{2}\bigl[\dot{V} + L_{2}(\dot{\psi} + \dot{ \theta}_{2})^{2}\cos \theta_{2} \\ &\quad- 2V(\dot{\psi} + \dot{\theta}_{2})\sin \theta_{2}\bigr] + GMm_{1} / r^{2} \\ &\quad+ GMm(r + L_{1}\cos \theta_{1}) / R_{m}^{3}\\ &\quad + GMm_{2}(r + L_{1}\cos \theta_{1} + L_{2}\cos \theta_{2}) / R_{2}^{3} \end{aligned}} \end{aligned}$$

(32)

$$\begin{aligned} &{ \begin{aligned}[b] N_{2} &= 2(m_{1} + m_{2} + m)r\dot{r}\dot{\psi} \\ &\quad+ (m_{2} + m) \{ 2L_{1}V(\dot{\psi} + \dot{ \theta}_{1}) \\ &\quad+ 2\bigl[L_{1}\dot{r}\dot{\psi} + Vr(\dot{ \psi} + \dot{\theta}_{1})\bigr]\cos \theta_{1} \\ &\quad + \bigl[\dot{V}r - L_{1}\bigl(2r\dot{\psi} \dot{ \theta}_{1} + r\dot{\theta}_{1}^{2}\bigr)\bigr] \sin \theta_{1} \} \\ &\quad+ m_{2} \bigl\{ - 2L_{2}V(\dot{\psi} + \dot{\theta}_{2}) \\ &\quad - \bigl[2Vr(\dot{\psi} + \dot{ \theta}_{2}) - 2L_{2}\dot{r}\dot{\psi} \bigr]\cos \theta_{2} \\ &\quad- \bigl[\dot{V}r + L_{2}\bigl(2r\dot{\psi} \dot{\theta}_{2} + r\dot{\theta}_{2}^{2}\bigr)\bigr]\sin \theta_{2}\\ & \quad+ \bigl[2L_{2}V(\dot{\psi} + \dot{\theta}_{1}) - 2L_{1}V(\dot{\psi} + \dot{\theta}_{2})\bigr]\\ &\quad\times \cos ( \theta_{2} - \theta_{1}) \\ &\quad - \bigl[L\dot{V} + L_{1}L_{2}(\dot{ \theta}_{2} - \dot{\theta}_{1}) (2\dot{\psi} + \dot{ \theta}_{1} + \dot{\theta}_{2})\bigr]\\ &\quad\times\sin ( \theta_{2} - \theta_{1}) \bigr\} \end{aligned}} \end{aligned}$$

(33)

$$\begin{aligned} &{ \begin{aligned}[b] N_{3} &= (m_{2} + m)L_{1}\bigl[2V(\dot{\psi} + \dot{\theta}_{1}) \\ &\quad+ 2\dot{r}\dot{\psi} \cos \theta_{1} + r \dot{\psi}^{2}\sin \theta_{1}\bigr]\\ &\quad + m_{2}L_{1} \bigl\{ \bigl[ - 2V(\dot{\psi} + \dot{\theta}_{2})\bigr]\cos ( \theta_{2} - \theta_{1}) \\ &\quad - \bigl[\dot{V} + L_{2}(\dot{\psi} + \dot{ \theta}_{2})^{2}\bigr]\sin (\theta_{2} - \theta_{1}) \bigr\} \\ &\quad- GMmL_{1}r\sin \theta_{1} / R_{m}^{3} \\ &\quad- GMm_{2}L_{1}\bigl[r\sin \theta_{1} - L_{2}\sin (\theta_{2} - \theta_{1})\bigr] / R_{2}^{3} \end{aligned}} \\ \end{aligned}$$

(34)

$$\begin{aligned} &{ \begin{aligned}[b] N_{4} &= m_{2}L_{2} \bigl\{ - 2V(\dot{\psi} + \dot{ \theta}_{2}) + 2\dot{r}\dot{\psi} \cos \theta_{2} \\ &\quad + r\dot{\psi}^{2}\sin \theta_{2} + 2V(\dot{\psi} + \dot{ \theta}_{1})\cos (\theta_{2} - \theta_{1}) \\ &\quad - \bigl[\dot{V} - L_{1}(\dot{\psi} + \dot{ \theta}_{1})^{2}\bigr]\sin (\theta_{2} - \theta_{1}) \bigr\} \\ &\quad - GMm_{2}L_{2}\bigl[r\sin \theta_{2} + L_{1}\sin (\theta_{2} - \theta_{1})\bigr] / R_{2}^{3} \end{aligned}} \end{aligned}$$

(35)