Parametric excitation of a thin ring under time-varying initial stress; theoretical and numerical analysis

Abstract

Initial stress in rings is one of the destructive effects which is almost inevitable due to various reasons such as being subsystems of a shrink-fitted joint, imperfections in the manufacturing, assembly or misalignment of the supporting mounts, and unbalancing in rotating condition. So, in this paper we focus on the effect of the initial stress and its variation with time on the dynamics of the pre-stressed ring. For this purpose, the equation of motion for in-plane bending vibration of a thin ring is derived using Hamilton’s principle. It is assumed that the initial stress is due to the distributed radially time-varying pressure. By representing the dynamic initial stress in the coefficients of the equation of motion; the equation is converted to Mathieu’s equation. The strained parameters method has been used to obtain the stability regions of motion and transition curves. Furthermore, to validate the obtained stability regions, numerical solutions of the equation of motion and Floquet theorem are used in some selected values of the parameters of the initial stress (magnitude of static and dynamic components of the initial stress). The fourth-order Runge-Kutta algorithm is used for numerical analysis of the equation of motion. The results show that the parameters of initial stress have direct impact on the stability of dynamic response. The obtained results from theoretical and numerical methods which are notably consistent with each other demonstrate that the initial stress, which has been almost always neglected in dynamic models of the systems, has a significant effect on the dynamics of the system, and it may even lead to an unstable dynamic response, while the excitation frequency is far enough from resonance region. So this paper can present the other application of modal analysis to non-destructive measure of initial stress.

Appendices

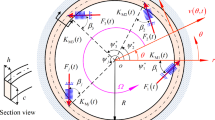
Appendix A: In-plane bending vibration of thin ring

In the in-plane bending-extensional vibration of the thin ring, the variation of the strain energy will be as follows [21]:

$$ \delta [ E_{s} ] = - \int_{s_{1}}^{s_{2}} \bigl\{ M\delta [ \chi_{\theta \theta} ] - \mathbf{N}\delta [ \eta_{\theta \theta} ] \bigr\}\,ds. $$

(29)

In which E _s , M, N are strain energy, bending moment and normal force, respectively. χ _θθ , η _θθ are bending and extensional strains, respectively, which are as follows:

$$ \chi_{\theta \theta} = \frac{\partial^{2}u}{\partial s^{2}} - \frac{1}{R}\frac{\partial v}{\partial s};\qquad \eta_{\theta \theta} = \frac{\partial v}{\partial s} + \frac{u}{R} $$

(30)

Also variation of the kinetic energy will be as:

$$\begin{aligned} \delta [ E_{k} ] = \int_{s_{1}}^{s_{2}} \rho A \{ \dot{u}\delta u + \dot{v}\delta v \}\,ds \end{aligned}$$

(31)

By substituting Eq. (30) in Eq. (29), the equation of motion in radial and tangential direction, respectively, will be obtained as:

$$\begin{aligned} &\rho A\ddot{u} - \frac{\partial^{2}M}{\partial s^{2}} + \frac{\mathbf{N}}{R} = 0 \end{aligned}$$

(32)

$$\begin{aligned} &\rho A\ddot{v} - \frac{1}{R}\frac{\partial M}{\partial s} - \frac{\partial \mathbf{N}}{\partial s} = 0 \end{aligned}$$

(33)

Where s=Rθ. Also, the circumferential moment-curvature relation is

$$ M = - \frac{EI}{R^{2}} \biggl( \frac{\partial^{2}u}{\partial \theta^{2}} - \frac{\partial v}{\partial \theta} \biggr) $$

(34)

By substituting Eq. (34) in Eq. (32) and Eq. (33), the final equations of motion will be as:

$$\begin{aligned} &{\rho A\ddot{u} + \frac{EI}{R^{4}} \biggl[ \frac{\partial^{4}u}{\partial \theta^{4}} - \frac{\partial^{3}v}{\partial \theta^{3}} \biggr] + \frac{\mathbf{N}}{R} = 0} \end{aligned}$$

(35)

$$\begin{aligned} &{\rho A\ddot{v} + \frac{EI}{R^{4}} \biggl[ \frac{\partial^{3}u}{\partial \theta^{3}} - \frac{\partial^{2}v}{\partial \theta^{2}} \biggr] - \frac{1}{R}\frac{\partial \mathbf{N}}{\partial \theta} = 0} \end{aligned}$$

(36)

Solving Eq. (35) for $\frac{\mathbf{N}}{R}$, it can be obtained as:

$$ \frac{\mathbf{N}}{R} = - \rho A\ddot{u} - \frac{EI}{R^{4}} \biggl[ \frac{\partial^{4}u}{\partial \theta^{4}} - \frac{\partial^{3}v}{\partial \theta^{3}} \biggr] $$

(37)

Substituting Eq. (37) into Eq. (36) and rearranging it, and applying the assumption of the thin ring as follows:

$$ \frac{\partial v}{\partial \theta} = - u $$

(38)

The following equation of motion can be obtained:

$$\begin{aligned} &{\frac{EI}{R^{4}}\frac{\partial^{6}v}{\partial \theta^{6}} + \biggl[ \frac{2EI}{R^{4}} \biggr] \frac{\partial^{4}v}{\partial \theta^{4}} + \biggl[ \frac{EI}{R^{4}} \biggr]\frac{\partial^{2}v}{\partial \theta^{2}}} \\ &{\quad{} - \rho A \biggl[ \frac{\partial^{2}v}{\partial t^{2}} - \frac{\partial^{4}v}{\partial \theta^{2}\partial t^{2}} \biggr] = 0} \end{aligned}$$

(39)

Appendix B: Floquet theorem

Mathematically, Eq. (40) has two linear, non-vanishing independent solutions as fundamental set of solutions u ₁(t),u ₂(t) [25].

$$ \ddot{f} ( t ) + ( \alpha + \varepsilon \cos \varOmega t )f ( t ) = 0 $$

(40)

Due to periodicity of (α+εcosΩt) then u ₁(t+T) and u ₂(t+T) are the fundamental solutions of Eq. (40), too. Hence

$$\begin{aligned} \bigl[\mathbf{u}(t + T)\bigr] =& [\mathbf{A}] \bigl[\mathbf{u}(t)\bigr] \to \left [ \begin{array}{c} u_{1} ( t + T ) \\ u_{2} ( t + T ) \end{array} \right ] \\ =& \left [ \begin{array}{c@{\quad}c} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right ]\left [ \begin{array}{c} u_{1} ( t ) \\ u_{2} ( t ) \end{array} \right ] \end{aligned}$$

(41)

Matrix [A] is not unique; it depends on the fundamental set being used. Now, according to Floquet theorem, if the fundamental solutions have the following property (λ is constant and may be complex):

$$ \left \{ \begin{array}{c} v_{1} ( t + T ) = \lambda_{1}v_{1} ( t ) \\ v_{2} ( t + T ) = \lambda_{2}v_{2} ( t ) \end{array} \right \} $$

(42)

Then, they are called Floquet solutions. In matrix form, it will be as:

$$\begin{aligned} \bigl[ \mathbf{v} ( t + T ) \bigr] =& [ \mathbf{B} ] \bigl[ \mathbf{v} ( t ) \bigr] \to \left [ \begin{array}{c} v_{1} ( t + T ) \\ v_{2} ( t + T ) \end{array} \right ] \\ =& \left [ \begin{array}{c@{\quad}c} \lambda_{1} & 0 \\ 0 & \lambda_{2} \end{array} \right ]\left [ \begin{array}{c} v_{1} ( t ) \\ v_{2} ( t ) \end{array} \right ] \end{aligned}$$

(43)

The solutions v ₁(t),v ₂(t) are known as Floquet solutions. λ ₁,λ ₂ would be Floquet multipliers. Now, Floquet solutions are related to u ₁(t),u ₂(t) by matrix [P] as follows:

$$ \bigl[ \mathbf{u} ( t ) \bigr] = [ \mathbf{P} ] \bigl[ \mathbf{v} ( t ) \bigr] $$

(44)

After some mathematical procedure, it is obtained:

$$ [ \mathbf{B} ] = [ \mathbf{P} ]^{ - 1} [ \mathbf{A} ] [ \mathbf{P} ] $$

(45)

It was concluded from Eq. (45), matrix of [B] is similar to [A]. So, they have the same eigenvalues. As it was clear from Eq. (43), the eigenvalues of the matrix [B] are λ ₁,λ ₂ or the Floquet multipliers.

The Floquet multipliers belong to the basic characteristics of the system under parametric excitation. They have key information of stability of the system as follows:

$$\begin{aligned} &{v_{i} ( t + nT ) = \lambda_{i}^{n}v_{i} ( t )} \\ &{\quad\Rightarrow v_{i} ( t ){} \to \left \{ \begin{array}{c} 0;\vert \lambda_{i} \vert < 1;\mathrm{stable} \\ \infty;\vert \lambda_{i} \vert > 1;\mathrm{unstable} \end{array} \right \}} \end{aligned}$$

(46)

The transition from stability to instability occurs for |λ _i |=1. On transition curve the solutions are periodic with T or 2T, (T is the period of (α+εcosΩt)).

$$ \vert \lambda_{i} \vert = 1 \Rightarrow \left \{ \begin{array}{l} \lambda = 1 \to v ( t + T ) = v ( t ) \\ \lambda = - 1 \to v ( t + T ) = - v ( t ) \end{array} \right \} $$

(47)

So, to stability analysis of the system, the Floquet multipliers should be derived, first. It is sufficient to obtain eigenvalues of the matrix [A]. To calculate matrix[A] members, Eq. (40) should be solved by initial condition as follows (I is the unity matrix):

$$ \bigl[ \mathbf{u} ( t = 0 ) \bigr] = \mathbf{I} $$

(48)

By substituting Eq. (48) in Eq. (41), it was obtained:

$$ [ \mathbf{A} ] = \bigl[ \mathbf{u} ( T ) \bigr] \to [ \mathbf{A} ] = \left [ \begin{array}{c@{\quad}c} u_{1} ( T ) & \dot{u}_{1} ( T ) \\ u_{2} ( T ) & \dot{u}_{2} ( T ) \end{array} \right ] $$

(49)

Then, by obtaining eigenvalues of matrix A, the Floquet multipliers are being defined.