Skip to main content
SpringerLink
Log in

Revealing the evolution, the stability, and the escapes of families of resonant periodic orbits in Hamiltonian systems

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

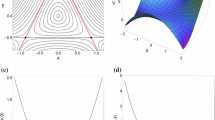
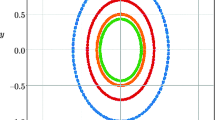
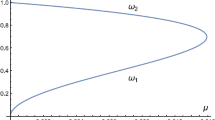
We investigate the evolution of families of periodic orbits in a bisymmetrical potential made up of a two-dimensional harmonic oscillator with only one quartic perturbing term, in a number of resonant cases. Our main objective is to compute sufficiently and accurately the position and the period of the periodic orbits. For the derivation of the above quantities (position and period) we deploy in each resonance case semi-numerical methods. The comparison of our semi-numerical results with those obtained by numerical integration of the equations of motion indicates that in every case the relative error is always less than 1 %, and therefore, the agreement is more than sufficient. Thus, we claim that semi-numerical methods are very effective tools for computing periodic orbits. We also study in detail the case when the energy of the orbits is larger than the escape energy. In this case, the periodic orbits in almost all resonance families become unstable and eventually escape from the system. Our target is to calculate the escape period and the escape position of the periodic orbits and also to monitor their evolution with respect to the value of the energy.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28
Fig. 29
Fig. 30
Fig. 31
Fig. 32
Fig. 33
Fig. 34
Fig. 35
Fig. 36
Fig. 37
Fig. 38
Fig. 39
Fig. 40
Fig. 41
Fig. 42
Fig. 43
Fig. 44
Fig. 45
Fig. 46
Fig. 47
Fig. 48
Fig. 49
Fig. 50

Similar content being viewed by others

References

  1. Aguirre, J., Viana, R.L., Sanjuán, A.F.: Fractal structures in nonlinear dynamics. Rev. Mod. Phys. 81(1), 333–386 (2009)

    Article  Google Scholar 

  2. Arribas, M., Elipe, A., Floria, L., Riaguas, A.: Oscillators in resonance p:q:r. Chaos Solitons Fractals 27, 1220–1228 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  3. Barbanis, B.: Escape regions of a quartic potential. Celest. Mech. Dyn. Astron. 48, 57–77 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  4. Belbruno, E., Llibre, J., Ollé, M.: On the families of periodic orbits which bifurcate from the circular Sitnikov motions. Celest. Mech. 60(1), 99–129 (1994)

    Article  MATH  Google Scholar 

  5. Caranicolas, N.D.: The 1:1 resonance in galactic type Hamiltonian systems. Astron. Astrophys. 267, 388–391 (1993)

    Google Scholar 

  6. Caranicolas, N.D.: A semi-numerical method for resonances in galactic-type Hamiltonians. Astron. Astrophys. 287, 752–756 (1994) (Paper I)

    Google Scholar 

  7. Caranicolas, N.D., Barbanis, B.: Periodic orbits in nearly axisymmetric stellar systems. Astron. Astrophys. 114, 360–366 (1982)

    MathSciNet  MATH  Google Scholar 

  8. Caranicolas, N.D., Karanis, G.I.: Chaos in barred galaxy models. Astrophys. Space Sci. 259, 45–56 (1998)

    Article  MATH  Google Scholar 

  9. Caranicolas, N.D., Karanis, G.I.: Motion in a potential creating a weak bar structure. Astron. Astrophys. 342, 389–394 (1999)

    Google Scholar 

  10. Caranicolas, N.D., Zotos, E.E.: Investigating the nature of motion in 3D perturbed elliptic oscillators displaying exact periodic orbits. Nonlinear Dyn. 69, 1795–1805 (2012)

    Article  MathSciNet  Google Scholar 

  11. Churchill, R.C., et al.: In: Casati, G., Fords, J. (eds.) Como Conference Proceedings on Stochastic Behavior in Classical and Quantum Hamiltonian Systems. Lecture Notes in Physics, vol. 93, p. 76. Springer, Berlin (1979)

    Chapter  Google Scholar 

  12. Contopoulos, G.: Orbits in highly perturbed dynamical systems. II. Stability of periodic orbits. Astron. J. 75(1), 108–130 (1970)

    Article  MathSciNet  Google Scholar 

  13. Contopoulos, G.: Asymptotic curves and escapes in Hamiltonian systems. Astron. Astrophys. 231(1), 41–55 (1990)

    MathSciNet  Google Scholar 

  14. Contopoulos, G.: Order and Chaos in Dynamical Astronomy. Springer, Berlin (2002)

    Book  MATH  Google Scholar 

  15. Contopoulos, G., Kaufmann, D.: Types of escapes in a simple Hamiltonian system. Astron. Astrophys. 253(2), 379–388 (1992)

    MathSciNet  MATH  Google Scholar 

  16. Contopoulos, G., Barbanis, B.: Periodic orbits and their bifurcations in a 3-D system. Celest. Mech. 59(3), 279–300 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  17. Contopoulos, G., Efstathiou, K.: Escapes and recurrence in a simple Hamiltonian system. Celest. Mech. Dyn. Astron. 88(2), 163–183 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  18. Contopoulos, G., Harsoula, M.: Systems with escapes. NYASA Newslett. 1045, 139–167 (2005)

    Google Scholar 

  19. Contopoulos, G., Patsis, P.A.: Outer dynamics and escapes in barred galaxies. Mon. Not. R. Astron. Soc. 369(3), 1039–1054 (2006)

    Article  Google Scholar 

  20. Deprit, A.: The Lissajous transformation. I. Basics. Celest. Mech. Dyn. Astron. 51(3), 202–225 (1991)

    Google Scholar 

  21. Deprit, A., Henrard, J.: Natural families of periodic orbits. Astron. J. 72(2), 158–172 (1967)

    Article  Google Scholar 

  22. Deprit, A., Elipe, A.: The Lissajous transformation. II. Normalization. Celest. Mech. Dyn. Astron. 51(3), 227–250 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  23. Fukushige, T., Heggie, D.C.: The time-scale of escape from star clusters. Mon. Not. R. Astron. Soc. 318(3), 753–761 (2000)

    Article  Google Scholar 

  24. Gilmore, R., Lefranc, M.: The Topology of Chaos. Wiley, New York (2002)

    MATH  Google Scholar 

  25. Giorgilli, A., Galgani, L.: From integrals from an autonomous Hamiltonian system near an equilibrium point. Celest. Mech. 17, 267–280 (1978)

    Article  MathSciNet  MATH  Google Scholar 

  26. Hénon, M., Heiles, C.: The applicability of the third integral of motion: some numerical experiments. Astron. J. 69(1), 73–79 (1964)

    Article  Google Scholar 

  27. Henrard, J., Lemaitre, A.: A perturbation method for problems with two critical arguments. Celest. Mech. 39, 213–238 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  28. Howell, K.C.: Three-dimensional periodic halo orbits. Celest. Mech. 32, 53–71 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  29. Kalantonis, V., Perdios, E.A., Perdiou, A.E.: The Sitnikov family and the associated families of 3D periodic orbits in the photogravitational RTBP with oblateness. Astrophys. Space Sci. 315(1–4), 323–334 (2008)

    Article  Google Scholar 

  30. Kandrup, H., Siopis, Ch., Contopoulos, G., Dvorak, R.: Diffusion and scaling in escapes from two-degrees-of-freedom Hamiltonian systems. Chaos 9(2), 381–392 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  31. Karanis, G.I., Vozikis, Ch.L.: Fast detection of chaotic behavior in galactic potentials. Astron. Nachr. 329(4), 403–412 (2007)

    Article  Google Scholar 

  32. Karimov, S.R., Sokolsky, A.G.: Periodic motions generated by Lagrangian solutions of the circular restricted three-body problem. Celest. Mech. 46(4), 335–381 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  33. Kazantsev, E.: Sensitivity of the attractor of the barotropic ocean model to external influences: approach by unstable periodic orbits. Nonlinear Process. Geophys. 8(4–5), 281–300 (2001)

    Article  Google Scholar 

  34. Peters, A.D., Jaffé, C., Delos, J.B.: Closed-orbit theory and the photodetachment cross section of H- in parallel electric and magnetic fields. Phys. Rev. A 56(1), 331–344 (1997)

    Article  Google Scholar 

  35. Press, W.H., Teukolsky, S.A., Vetterling, W.T., Flannery, B.P.: Numerical Recipes in FORTRAN. Cambridge University Press, Cambridge (1992)

    MATH  Google Scholar 

  36. Pyragas, K.: Control of chaos via an unstable delayed feedback controller. Phys. Rev. Lett. 86(11), 2265–2268 (2001)

    Article  MATH  Google Scholar 

  37. Russell, R.P.: Global search for planar and three-dimensional periodic orbits near Europa. J. Astronaut. Sci. 54(2), 199–226 (2006)

    Article  MathSciNet  Google Scholar 

  38. Saito, N., Ichimura, A.: In: Casati, G., Ford, J. (eds.) Stochastic Behavior in Classical and Quantum Hamiltonian Systems. Lecture Notes in Physics, vol. 93, p. 137. Springer, Berlin (1979)

    Chapter  Google Scholar 

  39. Scheeres, D.J.: Satellite dynamics about asteroids: computing the Poincaré map for the general case. In: Simó, C. (ed.) Hamiltonian Systems with Three or More Degrees of Freedom. NATO ASI Ser., vol. 533, p. 554 (1999)

    Chapter  Google Scholar 

  40. Siopis, Ch., Contopoulos, G., Kandrup, H.: Escape probabilities in a Hamiltonian with two channels of escape. NYASA Newslett. 751, 205–212 (1995)

    Google Scholar 

  41. Siopis, Ch., Kandrup, H., Contopoulos, G., Dvorak, R.: Universal properties of escape. NYASA Newslett. 773, 221–230 (1995)

    Google Scholar 

  42. Siopis, Ch., Kandrup, H., Contopoulos, G., Dvorak, R.: Universal properties of escape in dynamical systems. Celest. Mech. Dyn. Astron. 65(1–2), 57–68 (1996)

    MathSciNet  Google Scholar 

  43. Szebehely, V.: Theory of Orbits. Academic Press, New York (1967)

    Google Scholar 

  44. Voyatzis, G.: Chaos, order, and periodic orbits in 3:1 resonant planetary dynamics. Astrophys. J. 675(1), 802–816 (2008)

    Article  Google Scholar 

  45. Wisniacki, D.A., Vergini, E., Benito, R.M., Borondo, F.: Signatures of homoclinic motion in quantum chaos. Phys. Rev. Lett. 94(5), 054101 (2005)

    Article  Google Scholar 

  46. Zotos, E.E.: Trapped and escaping orbits in an axially symmetric galactic-type potential. Publ. Astron. Soc. Aust. 29, 161–173 (2012)

    Article  Google Scholar 

  47. Zotos, E.E.: Application of new dynamical spectra of orbits in Hamiltonian systems. Nonlinear Dyn. 69, 2041–2063 (2012)

    Article  MathSciNet  Google Scholar 

  48. Zotos, E.E., Caranicolas, N.D.: Are semi-numerical methods an effective tool for locating periodic orbits in 3D potentials? Nonlinear Dyn. 70, 279–287 (2012)

    Article  MathSciNet  Google Scholar 

  49. Zotos, E.E.: The fast norm vector indicator (FNVI) method: a new dynamical parameter for detecting order and chaos in Hamiltonian systems. Nonlinear Dyn. 70, 951–978 (2012)

    Article  MathSciNet  Google Scholar 

  50. Zotos, E.E., Carpintero, D.D.: Orbit classification in a disk galaxy model with a spherical nucleus (2013) (in press)

Download references

Acknowledgements

I would like to express my warmest thanks to the two anonymous referees for their careful reading of the manuscript and for their very positive comments and apt suggestions, which allowed us to improve both the quality and the clarity of this article.

Author information

Authors and Affiliations

  1. Department of Physics, School of Science, Aristotle University of Thessaloniki, 541 24, Thessaloniki, Greece

    Euaggelos E. Zotos

Authors
  1. Euaggelos E. Zotos
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Euaggelos E. Zotos.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Zotos, E.E. Revealing the evolution, the stability, and the escapes of families of resonant periodic orbits in Hamiltonian systems. Nonlinear Dyn 73, 931–962 (2013). https://doi.org/10.1007/s11071-013-0844-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-013-0844-5

Keywords

Search

Navigation