Output feedback stabilization of the inverted pendulum system: a Lyapunov approach

Abstract

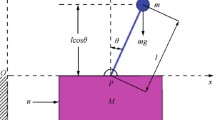
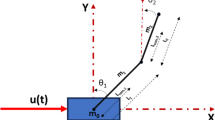
In this work, we present an output feedback stabilization method for the Inverted Pendulum Cart (IPC) system around its unstable equilibrium point. The pendulum is initialized in the upper-half plane, and the position of the cart and the pendulum angular positions are always available. Our strategy was accomplished introducing a suitable coordinate change to obtain a nonlinear version of the original system, which is affine in the unmeasured velocities state. This fact allows us to adapt an observer based controller devoted to render the closed-loop system to the origin. The proposed observer based controller was designed using the direct Lyapunov method. This allows estimating the corresponding attraction domain for the whole system, which can be as large or as small as desired. While the corresponding closed-loop stability analysis was made using the LaSalle Invariance Theorem. Convincing numerical simulations were included to show the performance of the closed-loop system.

Appendix

Verification of system (4)

Evidently, verifying the first two equations of system (4) is quite simple. The corresponding value of $\dot{p}_{1}$ is directly obtained by substituting the transformation (3) in the first equation of system (2). Now, from transformation (3), it is very easy to verify the following equality:

$$ \dot{p}_{2}=\ddot{z}-\frac{\sin \theta \dot{\theta}^{2}}{1+\delta }+\frac{\cos \theta \ddot{\theta}}{1+\delta }. $$

(46)

And, observing that the accelerations $\ddot{\theta}$ and $\ddot{z}$, straightforwardly obtained from the normalized system (2), are given by

then substituting these accelerations into (46), we have, after some simple algebra, that $\dot{p}_{2}=u/(1+\delta )$.

Convexity and boundedness of the set $\varPhi (\rho )\leq \widetilde{c}$

From (23) and (24), we have that Φ can be expressed as

$$ \varPhi (\rho )=\beta_{k}\log \biggl( \frac{\psi (0)}{\psi (\rho_{1})} \biggr) +\frac{k_{p}}{2}\rho_{2}^{2}, $$

where the coordinate map ρ=(q ₁=ρ ₁,ρ ₂=q ₂+ϒ(q ₁)) is a one-to-one transformation, as long as ρ ₁∈I ₀. Hence, V is strictly positive definite and proper on the set $(\rho_{1},\rho_{2})\in (-\overline{\theta },\overline{\theta })\times \mathbb{R}$.

In order to show that the set Φ(ρ)≤ $\widetilde{c}$ is a bounded and convex set, we must note that if Φ(ρ)< $\widetilde{c}=\beta_{k}\log ( \psi (0)/\psi (\overline{\theta }) )$, then $\psi (\overline{\theta })<\psi (\rho_{1})$. Now remembering that (1+δ)k ₂>k ₃>0 and from the definition of $\ \overline{\theta }$ and ε (see (27)), we have that

$$ 0<\varepsilon =\psi (\overline{\theta })<\psi (\rho_{1})=-k_{3}+(1+ \delta )k_{2}\cos \rho_{1}, $$

which implies that ρ ₁∈I ₀. Observe that the strict inequality excludes the singular points

$$ -k_{3}+(1+\delta )k_{2}\cos \overline{q}_{1}=0, $$

where $\overline{q}_{1}\in (\overline{\theta },\pi /2) \cup (-\pi /2,-\overline{\theta })$. In a similar way, we can show that $\vert \rho_{2}\vert \leq \sqrt{2\widetilde{c}/k_{p}}$. On the other hand, it is easy to check that the Hessian of Φ(ρ) is given by

$$ \nabla_{\rho }^{2}\varPhi (q_{1},\rho_{2})= \left [ \begin{array}{c@{\quad}c} \frac{\beta_{k}(1+\delta )k_{2}\psi (\rho_{1})}{\psi (\rho_{1})^{2}} & 0 \\ 0 & k_{p}\end{array} \right ] . $$

In fact, this Hessian is strictly positive for all ρ ₁∈I ₀. Therefore, Φ(ρ)≤c with $0<c<\widetilde{c}$ is a bounded and convex set. Consequently, Φ(ρ) is positive definite and proper throughout the set W _c given in (28).