Abstract
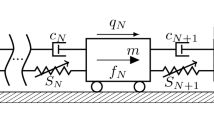
In the first part of this study, the basic steps of a methodology are presented, leading to a long time response of a class of periodically excited mechanical models with contact and dry friction. In particular, the models examined belong to the special class of Filippov-type dynamical systems, which possess continuous displacements and velocities, but exhibit discontinuities in their accelerations. The direct determination of periodic steady state response of this class of models is achieved by combining suitable numerical integration of the equations of motion with an appropriate technique yielding the corresponding monodromy matrix. This matrix, which arises from a linearization of the motion around a located periodic solution, involves saltations (jumps) and is also useful in predicting its stability properties. The analytical part is complemented by a suitable continuation procedure, enabling evaluation of complete branches of periodic motions. In the second part of the study, the effectiveness of the methodology developed is confirmed by presenting representative sets of numerical results obtained for selected examples. The first two of them are single degree of freedom oscillators. Besides investigating some interesting aspects of regular periodic response, some cases involving rich dynamics of the class of the system examined are also studied in a systematic way. The last example is a more involved and challenging model, related to the function of an engine valve and characterized by large numerical stiffness.
Similar content being viewed by others
References
Nayfeh, A.H., Mook, D.T.: Nonlinear Oscillation. Wiley, New York (1979)
Craig, R.R. Jr.: Structural Dynamics—An Introduction to Computer Methods. Wiley, New York (1981)
Wiggins, S.: Introduction to Applied Nonlinear Dynamical Systems and Chaos. Springer, New York (1990)
Nayfeh, A.H., Balachandran, B.: Applied Nonlinear Dynamics. Wiley, New York (1990)
Shaw, S.W.: On the dynamic response of a system with dry friction. J. Sound Vib. 108, 305–325 (1986)
Karyeaclis, M., Caughey, T.K.: Stability of a semi-active impact damper. J. Appl. Mech. 56, 453–464 (1989)
Natsiavas, S.: Periodic response and stability of oscillators with symmetric trilinear restoring force. J. Sound Vib. 134, 315–331 (1989)
Natsiavas, S.: Dynamics of piecewise linear oscillators with van der Pol type damping. Int. J. Non-Linear Mech. 26, 349–366 (1991)
Dankowicz, H., Nordmark, A.B.: On the origin and bifurcations of stick-slip oscillations. Physica D 136, 280–302 (2000)
Fidlin, A., Thomsen, J.J.: Predicting vibration-induced displacement for a resonant friction slider. Eur. J. Mech. A, Solids D 20, 155–166 (2001)
Luo, A.C.J.: Grazing and chaos in a periodically forced piecewise linear oscillator. J. Vib. Acoust. 128, 28–34 (2006)
Moreau, J.J., Panagiotopoulos, P.D.: Non-Smooth Mechanics and Applications. Springer, Vienna (1996)
Jean, M.: The non-smooth contact dynamics method. Comput. Methods Appl. Mech. Eng. 177, 235–257 (1999)
Pfeiffer, F., Glocker, C.: Multibody Dynamics with Unilateral Contacts. Wiley, New York (1996)
Brogliato, B.: Non-Smooth Mechanics, 2nd edn. Springer, Berlin (1999)
Glocker, C.: Set-Valued Force Laws, Dynamics of Non-Smooth Systems. Springer, Berlin (2001)
Leine, R.I., Nijmeijer, H.: Dynamics and Bifurcations of Non-Smooth Mechanical Systems. Springer, Berlin (2004)
Doedel, E.: AUTO: Software for Continuation and Bifurcation Problems in Ordinary Differential Equations. California Institute of Technology, Pasadena (1986)
Fey, R.H.B., van Campen, D.H., de Kraker, A.: Long term structural dynamics of mechanical systems with local nonlinearities. J. Vib. Acoust. 118, 147–153 (1996)
Chen, C.S., Natsiavas, S., Nelson, H.D.: Coupled lateral-torsional vibration of a gear-pair system supported by a squeeze film damper. J. Vib. Acoust. 120, 860–867 (1998)
Theodosiou, C., Natsiavas, S.: Dynamics of finite element structural models with multiple unilateral constraints. Int. J. Non-Linear Mech. 44, 371–382 (2009)
Leine, R.I., van Campen, D.H., de Kraker, A., van den Steen, L.: Stick-slip vibrations induced by alternate friction models. Nonlinear Dyn. 16, 41–54 (1998)
Theodosiou, C., Sikelis, K., Natsiavas, S.: Periodic steady state response of large scale mechanical models with local nonlinearities. Int. J. Solids Struct. 46, 3565–3576 (2009)
Fried, I.: Orthogonal trajectory accession to the nonlinear equilibrium curve. Comput. Methods Appl. Mech. Eng. 47, 283–297 (1984)
Wempner, G.A.: Discrete approximations related to nonlinear theories of solids. Int. J. Solids Struct. 7, 1581–1599 (1971)
Riks, E.: An incremental approach to the solution of snapping and buckling problems. Int. J. Solids Struct. 15, 529–551 (1979)
Natsiavas, S., Verros, G.: Dynamics of oscillators with strongly nonlinear asymmetric damping. Nonlinear Dyn. 20, 221–246 (1991)
Begley, C.J., Virgin, L.N.: A detailed study of the low frequency periodic behaviour of a dry friction oscillator. J. Dyn. Syst. Meas. Control 119, 481–487 (1997)
Natsiavas, S.: Stability of piecewise linear oscillators with viscous and dry friction damping. J. Sound Vib. 217, 507–522 (1998)
Golub, G.H., van Loan, C.F.: Matrix Computations. University Press, Baltimore (1996)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Theodosiou, C., Pournaras, A. & Natsiavas, S. On periodic steady state response and stability of Filippov-type mechanical models. Nonlinear Dyn 66, 355–376 (2011). https://doi.org/10.1007/s11071-011-0080-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-011-0080-9