Skip to main content
SpringerLink
Log in

Extended double Wronskian solutions to the Whitham–Broer–Kaup equations in shallow water

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

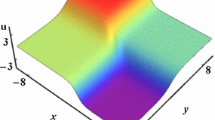
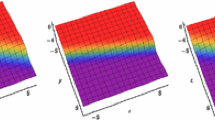
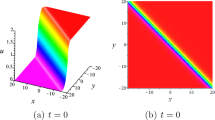
Whitham–Broer–Kaup (WBK) equations describing the propagation of shallow-water waves, with a variable transformation, are transformed into a generalized Ablowitz–Kaup–Newell–Segur system, the bilinear forms of which are obtained via the rational transformations. Employing the matrix extension and symbolic computation, we derive types of solutions of the WBK equations through the selection of different canonical matrices, including solitons, rational solutions, and complexitons. Furthermore, dynamic properties of the solutions are discussed graphically and a novel phenomenon is observed, i.e., the coexistence of the elastic–inelastic interactions without disturbing each other.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Whitham, G.B.: Variational methods and applications to water waves. Proc. R. Soc. A 299, 6–25 (1967)

    Article  MATH  Google Scholar 

  2. Broer, L.J.: Approximate equations for long water waves. Appl. Sci. Res. 31, 377–395 (1975)

    Article  MathSciNet  MATH  Google Scholar 

  3. Kaup, D.J.: A higher-order water wave equation and method for solving it. Theor. Phys. 54, 396–408 (1975)

    MathSciNet  MATH  Google Scholar 

  4. Kupershmidt, B.A.: Mathematics of dispersive water waves. Commun. Math. Phys. 99, 51–73 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  5. Ablowitz, M.J.: Soliton, Nonlinear Evolution Equations and Inverse Scattering. Cambridge University Press, New York (1991)

    Book  Google Scholar 

  6. Xu, T., Zhang, H.Q., Zhang, Y.X., Yao, Z.Z., Tian, B.: New extension of the tanh-function method and application to the Whitham–Broer–Kaup shallow water model with symbolic computation. Phys. Lett. A 369, 458–463 (2007)

    Article  Google Scholar 

  7. Zhang, J.F., Guo, G.P., Wu, F.M.: New multi-soliton solutions and travelling wave solutions of the dispersive long-wave equations. Chin. Phys. 11, 533 (2002)

    Article  Google Scholar 

  8. Shen, J.W., Xu, W.: Bifurcation method and travelling wave solution to Whitham–Broer–Kaup equation. Appl. Math. Comput. 171, 677–702 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  9. Xie, F.D., Cao, X.S.: A computational approach to the new type solutions of Whitham–Broer–Kaup equation in shallow water. Commun. Theor. Phys. 41, 179–182 (2004)

    MATH  Google Scholar 

  10. Chen, Y., Wang, Q., Li, B.A.: A generalized method and general form solutions to the Whitham–Broer–Kaup equation. Chaos Solitons Fractals 22, 675–682 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  11. Chen, Y., Wang, Q.: Multiple Riccati equations rational expansion method and complexiton solutions of the Whitham–Broer–Kaup equation. Phys. Lett. A 347, 215–227 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  12. Wang, L., Gao, Y.T., Gai, X.L., Sun, Z.Y.: Inelastic interactions and double Wronskian solutions for the Whitham–Broer–Kaup model in shallow water. Phys. Scr. 80, 065017 (2009)

    Article  Google Scholar 

  13. Lin, J., Xu, Y.S., Wu, F.M.: Evolution property of soliton solutions for the Whitham–Broer–Kaup equation and variant Boussinesq equation. Chin. Phys. 12, 1049–1053 (2003)

    Article  Google Scholar 

  14. Hong, W.P.: Spherical Kadomtsev–Petviashvili equation and nebulons for dust ion-acoustic waves with symbolic computation. Phys. Lett. A 361, 520–522 (2007)

    Article  MATH  Google Scholar 

  15. Tian, B., Gao, Y.T.: Spherical nebulons and Bäcklund transformation for a space or laboratory un-magnetized dusty plasma with symbolic computation. Eur. Phys. J. D 33, 59–65 (2005)

    Article  Google Scholar 

  16. Das, G., Sarma, J.: A new mathematical approach for finding the solitary waves in dusty plasma. Phys. Plasmas 6, 4392–4394 (1999)

    Article  MathSciNet  Google Scholar 

  17. Tian, B., Wei, G.M., Zhang, C.Y., Shan, W.R., Gao, Y.T.: Transformations for a generalized variable-coefficient Korteweg–de Vries model from blood vessels, Bose–Einstein condensates, rods and positons with symbolic computation. Phys. Lett. A 356, 8–16 (2006)

    Article  MATH  Google Scholar 

  18. Barnett, M.P., Capitani, J.F., Von Zur Gathen, J., Gerhard, J.: Symbolic calculation in chemistry: selected examples. Int. J. Quant. Chem. 100, 80–104 (2004)

    Article  Google Scholar 

  19. Tian, B., Shan, W.R., Zhang, C.Y., Wei, G.M., Gao, Y.T.: Transformations for a generalized variable-coefficient nonlinear Schrödinger model from plasma physics, arterial mechanics and optical fibers with symbolic computation. Eur. Phys. J. B 47, 329–332 (2005)

    Article  Google Scholar 

  20. Tam, H.W., Ma, W.X., Wang, D.L.: The Hirota–Satsuma coupled KdV equation and a coupled Ito system revisited. J. Phys. Soc. Jpn. 69, 45–51 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  21. Hirota, R., Satsuma, J.: Solitary wave solutions for a generalized Hirota–Satsuma coupled KdV equation by homotopy perturbation method. Phys. Lett. A 85, 407–408 (1981)

    Article  MathSciNet  Google Scholar 

  22. Lou, S.Y., Tang, X.Y., Lin, J.: Similarity and conditional similarity reductions of a (2+1)-dimensional KdV equation via a direct method. J. Math. Phys. 41, 8286–8303 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  23. Wadati, M.: Wave propagation in nonlinear lattice. J. Phys. Soc. Jpn. 38, 673–680 (1975)

    Article  MathSciNet  Google Scholar 

  24. Matveev, V.B., Salle, M.A.: Darboux Transformation and Soliton. Springer, Berlin (1991)

    Google Scholar 

  25. Dubrovsky, V.G., Konopelchenko, B.G.: Delta-dressing and exact solutions for the (2+1)-dimensional Harry Dym equation. J. Phys. A 27, 4619 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  26. Freeman, N.C., Nimmo, J.J.: Soliton solutions of the Korteweg–de Vries and Kadomtsev–Petviashvili equations: the Wronskian technique. Phys. Lett. A 95, 1–13 (1983)

    Article  MathSciNet  Google Scholar 

  27. Matveev, V.B.: Generalized Wronskian formula for solutions of the KdV equations: first applications. Phys. Lett. A 166, 205–208 (1992)

    Article  MathSciNet  Google Scholar 

  28. Ablowitz, M.J., Kaup, D.J., Newell, A.C.: The inverse scattering transform-Fourier analysis for nonlinear problems. Stud. Appl. Math. 53, 249–315 (1974)

    MathSciNet  Google Scholar 

  29. Ma, W.X., You, Y.C.: Solving the Korteweg–de Vries equation by its bilinear form: Wronskian solutions. Trans. Am. Math. Soc. 357, 1753–1778 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  30. Yao, Y.Q., Ji, J., Liu, Y.Q., Chen, D.Y.: Novel Wronskian solutions to Boussinesq equation. Nonlinear Anal. 48, 577–583 (2007)

    MathSciNet  Google Scholar 

  31. Ge, J.Y., Zhang, Y., Chen, D.Y.: Extended Wronskian formula for solutions to the Korteweg–de Vries equation. J. Phys. 96, 012071 (2008)

    Google Scholar 

  32. Ablowitz, M.J., Satsuma, J.: Solitons and rational solutions of nonlinear evolution equations. J. Math. Phys. 19, 2180–2186 (1978)

    Article  MathSciNet  MATH  Google Scholar 

  33. Siranunpiboon, S., Howard, S.D., Roy, S.K.: A note on the Wronskian form of solutions of the KdV equation. Phys. Lett. A 134, 31–33 (1988)

    Article  MathSciNet  Google Scholar 

  34. Chen, D.Y., Zhang, D.J., Bi, J.B.: New double Wronskian solutions of the AKNS equation. Sci. China, Math. 51, 55–69 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  35. Hirota, R., Satsuma, J.: Soliton solutions of a coupled Korteweg–de Vries equation. J. Phys. Soc. Jpn. 85, 407–408 (1981)

    MathSciNet  Google Scholar 

  36. Yao, Y.Q., Zhang, D.J., Chen, D.Y.: The double Wronskian solutions to the Kadomtsev–Petviashvili equation. Phys. Lett. B 9, 621–641 (2008)

    Google Scholar 

  37. Zhang, C., Tian, B., Meng, X.H., Lü, X., Cai, K.J., Geng, T.: Painlevé integrability and N-soliton solution for the Whitham–Broer–Kaup shallow water model using symbolic computation. Z. Naturforsch. A 63, 253–261 (2008)

    Google Scholar 

  38. Zhang, D.J., Chen, D.Y.: Negatons, positons, rational-like solutions and conservation laws of the Korteweg–de Vries equation with loss and non-uniformity terms. J. Phys. A 37, 851–865 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  39. Liu, W.J., Tian, B., Zhang, H.Q., Li, L.L., Xue, Y.S.: Soliton interaction in the higher-order nonlinear Schrodinger equation investigated with Hirota’s bilinear method. Phys. Rev. E 77, 066605 (2008)

    Article  MathSciNet  Google Scholar 

  40. Liu, W.J., Tian, B., Zhang, H.Q.: Types of solutions of the variable-coefficient nonlinear Schrodinger equation with symbolic computation. Phys. Rev. E 78, 066613 (2008)

    Article  MathSciNet  Google Scholar 

  41. Zhang, H.Q., Xu, T., Li, J., Tian, B.: Integrability of an N-coupled nonlinear Schrödinger system for polarized optical waves in an isotropic medium via symbolic computation. Phys. Rev. E 77, 026605 (2008)

    Article  MathSciNet  Google Scholar 

  42. Zhang, H.Q., Tian, B., Xu, T., Li, H., Zhang, C., Zhang, H.: Lax pair and Darboux transformation for multi-component modified Korteweg-de Vries equations. J. Phys. A 41, 355210 (2008)

    Article  MathSciNet  Google Scholar 

  43. Xu, T., Tian, B., Li, L.L., Lü, X., Zhang, C.: Dynamics of Alfvén solitons in inhomogeneous plasmas. Phys. Plasmas 15, 102307 (2008)

    Article  Google Scholar 

  44. Xu, T., Tian, B.: Bright N-soliton solutions in terms of the triple Wronskian for the coupled nonlinear Schrödinger equations in optical fibers. J. Phys. A 43, 245205 (2010)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Ministry-of-Education Key Laboratory of Fluid Mechanics and National Laboratory for Computational Fluid Dynamics, Beijing University of Aeronautics and Astronautics, Beijing, 100191, China

    Guo-Dong Lin, Yi-Tian Gao, Xiao-Ling Gai & De-Xin Meng

  2. State Key Laboratory of Software Development Environment, Beijing University of Aeronautics and Astronautics, Beijing, 100191, China

    Yi-Tian Gao

Authors
  1. Guo-Dong Lin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yi-Tian Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xiao-Ling Gai
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. De-Xin Meng
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yi-Tian Gao.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Lin, GD., Gao, YT., Gai, XL. et al. Extended double Wronskian solutions to the Whitham–Broer–Kaup equations in shallow water. Nonlinear Dyn 64, 197–206 (2011). https://doi.org/10.1007/s11071-010-9857-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-010-9857-5

Keywords

Search

Navigation