Skip to main content
SpringerLink
Log in

Comparison of annual maximum and peaks-over-threshold methods with automated threshold selection in flood frequency analysis: a case study for Australia

  • Original Paper
  • Published:
Natural Hazards Aims and scope Submit manuscript

Abstract

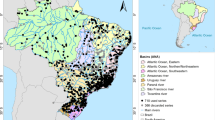
Flood frequency analysis (FFA) involves fitting of a probability distribution to observed flood data. Two main models, annual maximum (AM) and peaks over threshold (POT), are generally adopted in FFA. The POT model is underemployed due to its complexity and uncertainty associated with threshold selection and meeting independence criteria in selecting POT data series. This study evaluates the POT and AM models using data from 188 gauged stations in southeast Australia. The POT model adopted in this study applies different average numbers of events per year fitted with generalized Pareto (GP) distribution with an automated threshold detection method. For the AM model, the GP distribution is also adopted, and flood quantiles estimated by the two models are compared. It has been found that there are notable differences in design flood estimates between the AM and POT models. The study uses catchment characteristics data to understand the differences in quantile estimates between the AM and POT models. The percentage differences between the AM and POT models can be explained by mean annual rainfall (MAR) and mean annual evapotranspiration (MAE) (ARIs of 1.01–5 years), MAR (10-year ARI), stream density (SDEN) (for 20- and 50-year ARIs) and SDEN, main stream slope (S1085) and MAE (for 100-year ARI). Stations showing smaller % differences have relatively higher MAR and smaller MAE (indicating wetter condition); conversely, stations showing higher % differences have smaller MAR and higher MAE (drier condition).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Data availability

The analysis is carried out using R (R Core Team 2021) and POT package (Ribatet and Dutang 2019). The primary streamflow data series used in this study can be obtained from Australian Government agencies by paying a prescribed fee.

References

  • Bačová-Mitková V, Onderka M (2010) Analysis of extreme hydrological events on the sanube using the peak over threshold method. J Hydrol Hydromech 58(2):88–101

    Article  Google Scholar 

  • Ball JE, Babister MK, Nathan R, Weinmann PE, Weeks W, Retallick M et al (2016) Australian rainfall and runoff—A guide to flood estimation. Commonwealth of Australia, Canberra

    Google Scholar 

  • Bernardara P, Mazas F, Weiss J, Andreewsky M, Kergadallan X, Benoît M, Hamm L (2012) On the two step threshold selection for over-threshold modelling. Coast Eng Proc 1(33):1–6

    Google Scholar 

  • Bezak N, Brilly M, Šraj M (2014) Comparison between the peaks-over-threshold method and the annual maximum method for flood frequency analysis. Hydrol Sci J 59(5):959–977

    Article  Google Scholar 

  • Bhunya PK, Singh RD, Berndtsson R, Panda SN (2012) Flood analysis using generalized logistic models in partial duration series. J Hydrol 420–421:59–71

    Article  Google Scholar 

  • Bhuyan MK, Jena J, Bhunya PK (2016) At-site flood analysis using exponential and generalized logistic models in partial duration series (PDS). Int J Eng Technol 8(1):501–514

    Google Scholar 

  • Bobée B, Cavadias G, Ashkar F, Bernier J, Rasmussen PF (1993) Towards a systematic approach to comparing distributions used in flood frequency analysis. J Hydrol 142(1–4):121–136

    Article  Google Scholar 

  • Coles S (2001) An introduction to statistical modelling of extreme values. Springer, London

    Book  Google Scholar 

  • Curceac S, Atkinson PM, Milne A, Wu L, Harris P (2020) An evaluation of automated GPD threshold selection methods for hydrological extremes across different scales. J Hydrol 585:124845

    Article  Google Scholar 

  • Dowdy AJ, Mills GA, Timbal B, Griffiths M, Wang Y (2013) Understanding rainfall projections in relation to extratropical cyclones in eastern Australia. Aust Met Oceanogr J 63:355–364

    Article  Google Scholar 

  • Durocher M, Burn DH, Ashkar F (2019) Comparison of estimation methods for a nonstationary index-flood model in flood frequency analysis using peaks over threshold. Water Resour Res 55(11):9398–9416

    Article  Google Scholar 

  • Durocher M, Mostofi Zadeh S, Burn DH, Ashkar F (2018) Comparison of automatic procedures for selecting flood peaks over threshold based on goodness-of-fit tests. Hydrol Process 32(18):2874–2887

    Article  Google Scholar 

  • Gottschalk L, Krasovskaia I (2002) L-moment estimation using annual maximum (AM) and peak over threshold (POT) series in regional analysis of flood frequencies. Nor Geogr Tidsskr 56(2):179–187

    Article  Google Scholar 

  • Haddad, K, Rahman, A (2015), 'Estimation of large to extreme floods using a regionalization model', in Landscape Dynamics, Soils and Hydrological Processes in Varied Climates, pp 279–92

  • Haddad, K, Rahman, A, Kuczera, G, Weinmann, E (2012) 'A new regionalisation model for large flood estimation in Australia: Consideration of inter-site dependence in modelling', pp 969–76, Scopus

  • Haddad, K, Rahman, A, Weeks, W, Kuczera, G, Weinmann, PE (2011) 'Towards a new regional flood frequency analysis method for Western Australia', pp 3788–95, Scopus

  • Haddad, K, Zaman, M, Rahman, A, Shrestha, S (2010) 'Regional flood modelling: Use of Monte Carlo cross-validation for the best model selection', pp 2831–40, Scopus

  • Herath, S, Prasad Basnayake, A, Coremans, D (2015) 'Comparison of flood frequency analysis by annual maximum and peak over threshold approaches for Fitzroy River, Western Australia', pp 682–90, Scopus

  • Hosking JRM, Wallis JR (1987) Parameter and quantile estimation for the generalized pareto distribution. Technometrics 29(3):339–349

    Article  Google Scholar 

  • Ishak EH, Rahman A, Westra S, Sharma A, Kuczera G (2013) Evaluating the non-stationarity of australian annual maximum flood. J Hydrol 494:134–145

    Article  Google Scholar 

  • Karim F, Hasan M, Marvanek S (2017) Evaluating annual maximum and partial duration series for estimating frequency of small magnitude floods. Water (Switzerland) 9(7):481

    Google Scholar 

  • Khan S, Hussain I, Rahman A (2021) Identification of homogeneous rainfall regions in New South Wales, Australia. Tellus A Dyn Meteorol Oceanography 73(1):1–11

    Google Scholar 

  • Lang M, Ouarda TBMJ, Bobée B (1999) Towards operational guidelines for over-threshold modeling. J Hydrol 225(3):103–117

    Article  Google Scholar 

  • Langbein, WB (1949) 'Annual floods and the partial-duration flood series', Eos, Transactions American Geophysical Union, 30(6), 879–81, viewed 2020/06/12

  • Madsen H, Rasmussen PF, Rosbjerg D (1997) Comparison of annual maximum series and partial duration series methods for modeling extreme hydrologic events 1. At-site modeling. Water Resour Res 33(4):747–757

    Article  Google Scholar 

  • Mostofi Zadeh S, Durocher M, Burn DH, Ashkar F (2019) Pooled flood frequency analysis: a comparison based on peaks-over-threshold and annual maximum series. Hydrol Sci J 64(2):121–136

    Article  Google Scholar 

  • Önöz B, Bayazit M (2001) Effect of the occurrence process of the peaks over threshold on the flood estimates. J Hydrol 244(1–2):86–96

    Article  Google Scholar 

  • Pan, X, Rahman, A (2018) 'Comparison of annual maximum and peaks-over-threshold methods in flood frequency analysis', pp 614–25, Scopus

  • Pickands J (1975) Statistical inference using extreme order statistics. Ann Statist 3(1):119–131

    Google Scholar 

  • R Core Team (2021) R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. URL https://www.R-project.org/

  • Ribatet, M, Dutang, C (2019) POT: generalized pareto distribution and peaks over threshold. R package version 1.1–7

  • Robson, A, Reed, D (1999) Statistical Procedures for Flood Frequency Estimation, Flood Estimation Handbook, Centre for Ecology & Hydrology, Wallingford, UK

  • Thompson P, Cai Y, Reeve D, Stander J (2009) Automated threshold selection methods for extreme wave analysis. Coast Eng 56(10):1013–1021

    Article  Google Scholar 

  • USWRC (1976) Guidelines for determining flood flow frequency, US Department of the Interior, Geological Survey, Office of Water Data Coordination

Download references

Author information

Authors and Affiliations

  1. School of Engineering, Design and Built Environment, Western Sydney University, Building XB, Kingswood, Sydney, NSW, 2751, Australia

    Xiao Pan & Ataur Rahman

Authors
  1. Xiao Pan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ataur Rahman
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

XP developed the models, wrote computer programs, carried out analysis and drafted the manuscript, and AR checked the results and updated the manuscript by editing/rewriting.

Corresponding author

Correspondence to Ataur Rahman.

Ethics declarations

Conflict of interest

The authors declare that there is no conflicts of interest and the research did not involve any human participants and/or animals.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Information

Below is the link to the electronic supplementary material.

Supplementary file1 (DOCX 514 KB)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Pan, X., Rahman, A. Comparison of annual maximum and peaks-over-threshold methods with automated threshold selection in flood frequency analysis: a case study for Australia. Nat Hazards 111, 1219–1244 (2022). https://doi.org/10.1007/s11069-021-05092-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11069-021-05092-y

Keywords

Search

Navigation