Three-parameter generalized exponential distribution in earthquake recurrence interval estimation

Abstract

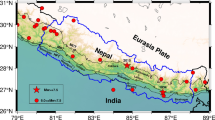
The purpose of this article is to study the three-parameter (scale, shape, and location) generalized exponential (GE) distribution and examine its suitability in probabilistic earthquake recurrence modeling. The GE distribution shares many physical properties of the gamma and Weibull distributions. This distribution, unlike the exponential distribution, overcomes the burden of memoryless property. For shape parameter  β> 1, the GE distribution offers increasing hazard function, which is in accordance with the elastic rebound theory of earthquake generation. In the present study, we consider a real, complete, and homogeneous earthquake catalog of 20 events with magnitude above 7.0 (Yadav et al. in Pure Appl Geophys 167:1331–1342, 2010) from northeast India and its adjacent regions (20°–32°N and 87°–100°E) to analyze earthquake inter-occurrence time from the GE distribution. We apply the modified maximum likelihood estimation method to estimate model parameters. We then perform a number of goodness-of-fit tests to evaluate the suitability of the GE model to other competitive models, such as the gamma and Weibull models. It is observed that for the present data set, the GE distribution has a better and more economical representation than the gamma and Weibull distributions. Finally, a few conditional probability curves (hazard curves) are presented to demonstrate the significance of the GE distribution in probabilistic assessment of earthquake hazards.

Appendices

Appendix 1

We put α = 1, γ = 0 in (3) for the sake of simplicity. Also, we replace the random variable T by U. Then, the corresponding density function becomes

$$ f_{GE} \left( {u;1,\beta ,0} \right) = \beta e^{ - u} \left( {1 - e^{ - u} } \right)^{\beta - 1} \quad \left( {u > 0,\beta > 0} \right) $$

(18)

Let M _U (x) denote the moment generating function (mgf). So, by definition

$$ M_{U} (x) = E\left( {e^{xU} } \right) = \beta \int\limits_{0}^{\infty } {e^{{\left( {x - 1} \right)u\,}} \left( {1 - e^{ - u} } \right)^{\beta - 1} {\text{d}}u} = \beta \frac{{\varGamma \left( \beta \right)\varGamma \left( {1 - x} \right)}}{{\varGamma \left( {\beta + 1 - x} \right)}}\quad \left( {x < 1} \right) $$

(19)

Therefore, the moment generating function M _T(x) of T(= αU + γ) ∼ GE(α, β, γ) is obtained as

$$ M_{T} (x) = E\left( {e^{xT} } \right) = \gamma e^{x\gamma } \frac{{\varGamma \left( {\beta + 1} \right)\varGamma \left( {1 - \alpha x} \right)}}{{\varGamma \left( {\beta + 1 - \alpha x} \right)}}\quad \left( {\alpha x < 1} \right) $$

(20)

Appendix 2

It is observed in Gupta and Kundu (1999) that g(α) in Eq. (17) is unimodal. Thus, in order to find its maximum value, we differentiate g(α) with respect to α and equate the resultant expression to zero. This yields the following equation in α.

$$ g^{{\prime }} \left( \alpha \right) = - \left( {n - 1} \right)\frac{{\sum\nolimits_{i = 2}^{n} {\left( {\frac{{t_{i} e^{{ - \frac{{t_{i}^{{\prime }} }}{\alpha }}} }}{{1 - e^{{ - \frac{{t_{i}^{{\prime }} }}{\alpha }}} }}} \right)} }}{{\sum\nolimits_{i = 2}^{n} {\ln \left( {1 - e^{{ - \frac{{t_{i}^{{\prime }} }}{\alpha }}} } \right)} }} + \left( {n - 1} \right)\alpha - \sum\limits_{i = 2}^{n} {\left( {\frac{{t_{i} e^{{ - \frac{{t_{i}^{{\prime }} }}{\alpha }}} }}{{1 - e^{{ - \frac{{t_{i}^{{\prime }} }}{\alpha }}} }}} \right)} - \sum\limits_{i = 2}^{n} {t_{i}^{{\prime }} } = 0 $$

(21)

Equation (21) can be solved in various ways, such as numerical techniques (e.g., fixed point iteration and the Newton-Raphson method) or by using any standard one-dimensional non-linear equation solver package. For completeness, we have provided schemes of the fixed point iteration and the Newton-Raphson methods below.

• (a) Fixed point iteration

We first write $g^{{\prime }} \left( \alpha \right) = 0\;{\text{as}}\;h\left( \alpha \right) = \alpha$ where,

$$ h\left( \alpha \right) = \left[ {\frac{{\sum\nolimits_{i = 2}^{n} {\left( {\frac{{t_{i} e^{{ - \frac{{t_{i}^{{\prime }} }}{\alpha }}} }}{{1 - e^{{ - \frac{{t_{i}^{{\prime }} }}{\alpha }}} }}} \right)} }}{{\sum\nolimits_{i = 2}^{n} {\ln \left( {1 - e^{{ - \frac{{t_{i}^{{\prime }} }}{\alpha }}} } \right)} }} + \frac{1}{n - 1}\sum\limits_{i = 2}^{n} {\left( {\frac{{t_{i}^{{\prime }} e^{{^{{ - \frac{{t_{i}^{{\prime }} }}{\alpha }}} }} }}{{1 - e^{{^{{ - \frac{{t^{\prime}_{i} }}{\alpha }}} }} }}} \right)} + \frac{1}{n - 1}\sum\limits_{i = 2}^{n} {t_{i}^{{\prime }} } } \right]^{\,} $$

(22)

Then, we apply the scheme of fixed point iteration as

$$ \alpha_{j + 1} = h\left( {\alpha_{j} } \right);\quad j = 1,2,{ \ldots } $$

(23)

• (b) Newton-Raphson method

Equation (21) can also be solved by the Newton-Raphson scheme for non-linear equation. The scheme is given as

$$ \alpha_{j + 1} = \alpha_{j} - \frac{{g^{{\prime }} \left( {\alpha_{j} } \right)}}{{g^{{\prime \prime }} \left( {\alpha_{j} } \right)}};\quad j = 1,2,{ \ldots } $$

(24)

Appendix 3

In the K-S test, we first construct the empirical distribution function H _n for n i.i.d. random variables T ₁, T ₂, ···, T _n as

$$ H_{n} \left( t \right) = \frac{1}{n}\sum\limits_{i = 1}^{n} {I_{{T_{i} \le t}} } $$

(25)

Here, $I_{{T_{i} \le t}}$ is the indicator function, equals 1 if T _i  ≤ t, and otherwise equals to 0. This makes H _n (t) a step function. Suppose we have two competitive models F and G. Then, the corresponding K-S distances are calculated as

$$ \begin{gathered} D_{1} = \mathop {sup}\limits_{ - \infty < t < \infty } \left| {H_{n} \left( t \right) - F\left( t \right)} \right| \hfill \\ D_{2} = \mathop {sup}\limits_{ - \infty < t < \infty } \left| {H_{n} \left( t \right) - G\left( t \right)} \right| \hfill \\ \end{gathered} $$

(26)

In the above expression, sup _t denotes the supremum of the set of distances. If D ₁ < D ₂, we choose model F; otherwise, we choose model G.

Appendix 4

For simplicity, we assume two competitive models F and G to describe the chi-square criterion. We further assume that $f\left( {t;\tilde{\theta }} \right)\;{\text{and}}\;g\left( {t;\tilde{\varphi }} \right)$ are the corresponding fitted models of F and G. In the chi-square test, we first divide the range of sample observations into k equal parts and record its observed frequencies. We then compute expected frequencies for all k parts using fitted models. Suppose the observed frequencies are n ₁, n ₂, …, n _k and expected frequencies are $f_{1} ,f_{2} ,{ \ldots },f_{k} \;{\text{and}}\;g_{1} ,g_{2} ,{ \ldots },g_{k}$ respectively, then we compute the chi-square distances between and {t ₁, t ₂, …, t _n }, $f\left( {t;\tilde{\theta }} \right)$ and {t ₁, t ₂, …, t _n }, $g\left( {t;\tilde{\varphi }} \right)$ as

$$ \begin{gathered} \chi_{\text{f,data}}^{2} = \sum\limits_{i = 1}^{k} {\frac{{\left( {n_{i} - f_{i} } \right)^{2} }}{{f_{i} }}} \hfill \\ \chi_{\text{g,data}}^{2} = \sum\limits_{i = 1}^{k} {\frac{{\left( {n_{i} - g_{i} } \right)^{2} }}{{g_{i} }}} \hfill \\ \end{gathered} $$

(27)

If χ ²_f,data  < χ ²_g,data then we choose model F; otherwise, we choose model G. The same approach can now be extended and used to prioritize a number of competitive models.