Efficiency assessment of the energy consumption and economic indicators in Beijing under the influence of short-term climatic factors: based on data envelopment analysis methodology

Abstract

In this paper, the data envelopment analysis (DEA) method is introduced to analyze the input–output efficiency of energy consumption and economic indicators in Beijing city under the influence of short-term climatic factors. Total energy consumption, fixed asset investment, average temperature, precipitation, sunshine hours, average wind velocity and the average pressure being employed as the input variables, gross domestic product (GDP) and per capita disposable income being employed as the output variables, effective technology and the validity of the scale of DEA of 31 decision-making units (DMUs) under the influence of the short-term climatic factors are analyzed, and the inefficient DMUs are improved. Empirical analysis shows that both energy consumption and economic growth are sensitive to short-term climate condition, and the reasonable employing of extreme climatic conditions is a question worthy of consideration. This study provides effective basis for the scientific and reasonable arrangement of Beijing city’s short-term climatic resources and energy–economic development.

1 Introduction

At the beginning of the twenty first century, the economy of Beijing city is in a high-speed development stage, and the energy consumption of Beijing city is also rising year by year. From 2000 to 2010, the GDP increases from 3,161.7 to 14,113.6 billion (RMB) yuan, while the total energy consumption increases from 4,144.0 to 6,954.1 million tons of standard coal in the Beijing area. Based on the standards of National Development and Reform Commission (China), industrial boilers burning one ton of coal will produce 2,620 kg of carbon dioxide, 8.5 kg of sulfur dioxide and 7.4 kg of nitrogen oxides. According to this standard, Beijing city consumed 6,954.1 million tons of standard coal and emitted 18,219,742 kg of carbon dioxide in 2010. Obviously, Beijing city’s economic development is at the cost of a large amount of energy consumption. The vast energy consumption will inevitably result in a serious deterioration of the atmospheric environment and will cause a short-term climate change. Data show that short-term climate change is sensitive to energy consumption and economic development. Conversely, short-term climate change will also have impact on energy consumption and economic development. For example, the impact of climate change on energy consumption has become an important research issue in World Climate Impact Research Project. At the same time, many studies have found that climate change had a significant impact on China’s winter heating conditions and energy demand since the mid-1990s (Li et al. 2006; Chen and Huang 2000; Luo and Niu 2012), etc. It can be clearly seen that the relations among energy, economy and climate are mutually restraint and mutually influence.

In recent years, many scholars try to explore the efficiency assessment method of energy consumption and economic indicator in China. For example, Lv et al. (2012) constructed a set of comprehensive evaluation index system of ecological environment of a coal-oriented city, applied the analytic hierarchy process to classify each evaluation factor and reflected ecological environmental quality of the coal-oriented city. Basing on the index decomposition analysis methodology, Zhou et al. (2007) introduced the macroscopic energy efficiency evaluation method. Zeng et al. (2008) employed the principal component analysis to build the coordinated development evaluation index system of region and comprehensively evaluated the coordinated regional development status of Beijing city, Tianjin city and Hebei Province. Jiang and Wu (2010) utilized the generalized method of moments method and ridge regression method to estimate the marginal efficiency of coal, oil, natural gas and electricity based on China’s inter-provincial panel data from 1996 to 2007 and analyzed the provincial energy consumption structure impact on the energy efficiency. The above research methods have two problems: One is energy efficiency options need to be selected by human judgment, which results in the research indicator affected by uncertainty human factor; other is all data of option indicators need hypothetical test, which increases the calculation difficulty.

When it is concerned with the efficient assessment of input–output conditions in China’s energy consumption and economic development, data envelopment analysis (DEA) can be better to avoid the two previous problems. On the one hand, DEA method can one-on-one depict energy consumption and economic growth indicators from a quantitative point of view, which avoids the artificial uncertainty of indicator selecting; on the other hand, DEA model has a completed constraint condition corresponding to the objective function, which needs not to consider the hypothetical test. Therefore, DEA method is highly respected by many scholars. For example, Wu and He (2006) evaluated the sustainable development of Beijing city’s energy and economic indicators over the past decade, obtained that Beijing region has the ability for sustainable development and proved that the energy and economic indicators in Beijing city possess the validity of the scale and technical efficiency. Wu and Wu (2009) established the evaluation index system of energy efficiency in China’s 30 administrative districts based on the energy efficiency evaluation model and proposed policies and measures for energy-saving and emission reduction. Huang et al. (2011) employed the DEA method to assess the regional vulnerability to natural hazards. Li (2010) explored the energy efficiency framework, method and model in the context of industrialization and economic growth and analyzed the China’s industrial sector data.

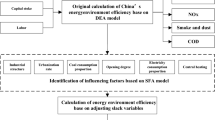
In summary, DEA method has many advantages on assessing the input–output conditions in China’s energy consumption and economic development. It can not only quantitatively calculate and compare relative efficiency with the different decision-making units (DMUs), but also without regard to hypothetical test the indicators of DMU. However, there are a few studies that take into account the sensitivity of short-term climatic factors to energy consumption and economic growth. From a new perspective, this paper attempts to adopt the DEA method to analyze input and output condition of energy consumption and economic indicators in Beijing under the influence on short-term climatic factors. Especially, this paper regards total energy consumption, fixed asset investment, average temperature, precipitation, sunshine hours, average wind velocity and the average pressure index as the input variables, and gross domestic product (GDP) and per capita disposable income as the output variables. This paper emphasizes the role of short-term climatic resource on the economic development of Beijing city and provides an efficient basis for scientific and rational allocation of short-term climatic resources and energy economic development in Beijing area.

2 Data envelopment analysis (DEA) methodology

Data envelopment analysis (DEA), as originally presented by Charnes et al. (1978, 1981) (C ² R), is a useful tool for measuring the relative efficiencies of decision-making units (DMUs) which produce multiple outputs by using multiple inputs. A best practice efficiency frontier composed of DMUs, which own the optimal efficiency over the datasets is constructed by DEA for comparative efficiency measurement. Those DMUs located at the efficiency frontier have their maximum outputs generated among all DMUs by taking the minimum level of inputs, which are efficient DMUs and own the best efficiency among all DMUs. The existing gap from any DMUs to the efficiency frontier shows how far the DMUs should be further improved to reach the optimal efficiency level (San Cristóbal Mateo 2012).

Charnes et al. (1978, 1981) and Cooper et al. (2011) describe DEA as follows: “mathematical programming model applied to observational data provides a new way of obtaining empirical estimates of relations—such as the production functions and/or efficient production possibility surfaces—that are cornerstones of modern economics”.

The classical DEA (C ² R) model for evaluating the efficiency of a DMU, denoted by DMU ₀ , is as follows:

$$ \begin{aligned} {\text{Max}}\,h_{0} = \sum\limits_{{r = 1}}^{s} {u_{r} y_{{r0}} } \\ & s.t\left\{ {\begin{array}{*{20}c} {\sum\limits_{{i = 1}}^{m} {v_{i} x_{{i0}} = 1} } \hfill \\ {\sum\limits_{{r = 1}}^{s} {u_{r} y_{{rj}} - \sum\limits_{{i = 1}}^{m} {v_{i} x_{{ij}} \le 0} } } \hfill \\ {u_{r} ,v_{i} \ge 0} \hfill \\ {\lambda _{j} \ge 0,\quad j = 1,2, \ldots ,n} \hfill \\ \end{array} } \right. \\ \end{aligned} $$

(1)

The Linear Programming dual problem of (1) is as follows:

$$ \begin{aligned} \theta ^{*} = {\text{min}}\:\theta \\ & s.t\left\{ {\begin{array}{*{20}c} {\sum\limits_{{j = 1}}^{n} {x_{{ij}} \lambda _{j} \le \theta x_{{i0}} \quad i = 1,2, \ldots ,m;} } \hfill \\ {\sum\limits_{{j = 1}}^{n} {y_{{rj}} \lambda _{j} \ge y_{{r0}} \quad r = 1,2, \ldots ,s;} } \hfill \\ {\lambda _{j} \ge 0,\quad j = 1,2, \ldots ,n.} \hfill \\ \end{array} } \right. \\ \end{aligned} $$

(2)

where $j$ is the DMU index, $j = (1,2, \ldots ,n);$ $r$ the output index, $r = (1,2, \ldots ,s);$ $i$ the input index, $i = (1,2, \ldots ,m);$ $x_{ij}$ the value of the $i$th input of the $j$th DMU; $y_{rj}$ the value of the $r$th output of the $j$th DMU; $u_{r}$ the weight given to the $r$th output; $v_{i}$ the weight given to the $i$th input; $\lambda_{j}$ is a weight variable; and $h_{0}$ and $\theta^{*}$ the relative efficiency of DMU ₀ . By virtue of the dual theorem of linear programming, we have $h_{0} = \theta^{*}$. A DMU ₀ is efficient if and only if $h_{0} = 1$ or $\theta^{*} = 1$. One can solve an equivalent optimization model (3) of (2) to obtain a relative efficiency score. The optimization model (3) is as follows:

$$ \begin{aligned} \theta ^{*} = {\text{min}}\:\theta - \varepsilon \left( {\sum\limits_{{i = 1}}^{m} {s_{i}^{ - } + \sum\limits_{{r = 1}}^{s} {s_{r}^{ + } } } } \right) \\ & s.t\left\{ {\begin{array}{*{20}c} {\sum\limits_{{j = 1}}^{n} {x_{{ij}} \lambda _{j} + s_{i}^{ - } = \theta x_{{i0}} } {\text{ }}} \hfill \\ {\sum\limits_{{j = 1}}^{n} {y_{{rj}} \lambda _{j} - s_{r}^{ + } = y_{{r0}} } } \hfill \\ {\lambda _{j} \ge 0,\quad s_{i}^{ - } ,s_{r}^{ + } ,} \hfill \\ {i = 1,2, \ldots ,m,\quad r = 1,2, \ldots ,s, \quad j = 1,2, \ldots ,n.} \hfill \\ \end{array} } \right. \\ \end{aligned} $$

(3)

where $s_{i}^{ - }$ and $s_{r}^{ + }$ are slack variables used to convert the inequalities in (2) to equivalent equations. Here, $\varepsilon > 0$ is a non-Archimedean element defined to be smaller than any positive real number. (We take $\varepsilon = 10^{ - 8}$ in this paper.)

2.1 The efficient analysis of the DMU (Banker et al. 1984; Wei 1988)

There are two kinds of efficiencies when evaluating the efficiency of a DMU. One is technical efficiency, and it is defined as a DMU making the best output by using the fix inputs such as capital, staff and technology; the other is scale efficiency, and a DMU is said to be scale efficient when its size of operations is optimal so that any modifications on its size will render the unit less efficient.

If we add a condition

$$ \sum\limits_{j = 1}^{n} {\lambda_{j} = 1} $$

(4)

to Model (2) or (3), and if the performance of a DMU is technically efficient if and only if both (i) $\theta^{*} = 1$ and (ii) all slacks $s_{i}^{ - } ,s_{r}^{ + } = 0$, the performance of a DMU is weakly technically efficient if and only if both (i) $\theta^{*} = 1$ and (ii) $s_{i}^{ - } \ne 0,$ and/or $s_{r}^{ + } \ne 0$ for some $i$ and $r$ in some alternate optima.

Let

$$ K = \sum {\lambda_{j} /\theta } $$

(5)

$K$ is called return to scale of the DMU ₀ . If $K = 1$, the DMU ₀ is constant return to scale (CRS, or scale efficiency), and the DMU would be technically efficient and operate at the most productive scale size. If $K < 1$, the DMU ₀ is increasing return to scale (IRS), and the smaller the value of $K$ is, the bigger the tendency of increasing return to scale would be. This indicates that if we change the input of $x_{ij}$ for some $i \in \left\{ {1,2, \ldots ,m} \right\}$, $j \in \left\{ {1,2, \ldots ,n} \right\}$ by the same proportion, the output $y_{rj}$ for some $r \in \left\{ {1,2, \ldots ,s} \right\}$, $j \in \left\{ {1,2, \ldots ,n} \right\}$ changes more than in proportion. If $K > 1$, the DMU ₀ is decreasing return to scale (DRS), and the larger the value of $K$ is, the bigger the tendency of decreasing return to scale would be. This indicates that if we change the input of $x_{ij}$ for some $i \in \left\{ {1,2, \ldots ,m} \right\}$, $j \in \left\{ {1,2, \ldots ,n} \right\}$ by the same proportion, the output $y_{rj}$ for some $r \in \left\{ {1,2, \ldots ,s} \right\}$, $j \in \left\{ {1,2, \ldots ,n} \right\}$ changes less than in proportion.

2.2 The improvement of an inefficient DMU

When $\theta^{*} < 1$ in Model (3), the performance of DMU ₀ is said to be inefficient. If a DMU ₀ is inefficient, we can adjust the values of the input and output such that the DMU ₀ is relatively efficient. In an input orientation one improves efficiency through proportional reduction in inputs, whereas an output orientation requires proportional augmentation of outputs. An inefficient DMU can be made more efficient by projection onto the frontier. That is, a transformation method is introduced by projecting $(x_{i0} ,y_{r0} )$ onto a relative efficient plane. Then we get a corresponding projection $(x^{\prime}_{i0} ,y^{\prime}_{r0} )$ such that the improved DMU ₀ is efficient. The transformation equations are as follows:

$$ \left\{ \begin{aligned} x_{i0}^{\prime} &= \theta^{*} x_{i0} - s_{i}^{ - } \\ y_{r0}^{\prime} &= y_{r0} + s_{r}^{ + } \end{aligned} \right. $$

(6)

2.3 The economic meaning of C ² R Model

The economic meanings of variables in C ² R Model (2) or (3) are as follows:

• 1. When $\theta^{*} = 1$ and $s_{i}^{ - } = s_{r}^{ + } = 0$ hold for all $i \in \left\{ {1,2, \ldots ,m} \right\}$, $r \in \left\{ {1,2, \ldots ,s} \right\}$, the performances of all DMUs are efficient. This indicates that the relative efficiency of the input–output of $n$ DMUs is optimal. When $\theta^{*} = 1$ and $s_{i}^{ - } = s_{r}^{ + } = 0$, the DMU ₀ is said to have technical efficiency, and when $K = 1$, the DMU ₀ is said to have scale efficiency.

• 2. When $\theta^{*} < 1$, and $s_{i}^{ - } \ne 0$ or $s_{r}^{ + } \ne 0$ hold for some $i \in \left\{ {1,2, \ldots ,m} \right\}$, $r \in \left\{ {1,2, \ldots ,s} \right\}$, the performance of DMU ₀ is inefficient. If $K < 1$, the DMU ₀ is increasing return to scale. And if $K > 1$, the $DMU_{0}$ is decreasing return to scale.

• 3. When $\theta^{*} = 1$, and $s_{i}^{ - } \ne 0$ or $s_{r}^{ + } \ne 0$ hold for some $i \in \left\{ {1,2, \ldots ,m} \right\}$, $r \in \left\{ {1,2, \ldots ,s} \right\}$, the performance of DMU ₀ is weakly efficient. This indicates that the DMU ₀ has not either technical efficiency or scale efficiency. $s_{i}^{ - } > 0$ holds for a $i \in \left\{ {1,2, \ldots ,m} \right\}$ shows that there is $s_{i}^{ - }$ in the value of the $i$th input $x_{ij}$ that still has not been adequately used. $s_{r}^{ + } > 0$ holds for a $r \in \left\{ {1,2, \ldots ,s} \right\}$ shows that there is $s_{r}^{ + }$ in the value of the $j$th output $y_{rj}$ that needs to be increased.

3 Empirical analysis

Using the DEA method, this section first regards short-term climatic factors, energy consumption and fixed asset investment as input variables, and gross domestic product (GDP) and per capita disposable income of urban residents as output variables based on Beijing city’s data from 1980 to 2010, then regards each year as a DMU and thus constructs DEA models to examine effective technology and scale efficiency of each DMU and to improve the inefficient DMUs.

3.1 Data sources, indicator selecting and processing

This section selects short-term climatic factors, energy consumption and economic indicators as the research variables based on Beijing city’s data from 1980 to 2010 (data are shown in Table 1). The data are originated from the “Beijing city Statistical Yearbook 1981–2011” and “China Meteorological Data Sharing Service System (National Meteorological Information Center 2011).” Main research indicators and input–output indicators are as follows:

Table 1 The empirical analysis data of short-term climatic factors, energy consumptions and economy indicators from 1980 to 2010 in Beijing city

• 1. Energy and economic indicators: total energy consumption (million tons of coal equivalent), fixed asset investment (a hundred million RMB yuan), GDP (a hundred million RMB yuan) and per capita disposable income (RMB yuan);

• 2. Meteorological indicators (short-term climatic factors): average temperature (°C), precipitation (mm), sunshine hours (hours), mean wind speed (m/s) and the average pressure (hpa).

Short-term climatic factors, energy consumption and economic indicators mentioned above belong to different input variables and output variables. Basing on these input–output variables, this paper views different years (1980–2010) in Beijing city as DMUs and evaluates the DEA efficiency of each DMU under the influence of the short-term climatic factors.

The total energy consumption is the number of all kinds of energy which is consumed by life, production throughout the whole country or region in a certain period. It reflects the level of energy consumption, composition and growth rate of the whole country or region. The amount of the energy input relates to benign development of the entire energy economy and energy system, and the main content is mainly concern about input efficiency of energy in the paper. Therefore, we regard total energy consumption as an input indicator.

Fixed asset investment is the primary means of social reproduction of fixed assets, through the activities of the construction and purchase of fixed assets. The national economy is continued to adopt the advanced technology and equipment to built emerging sectors. Through the efficient investment of fixed assets, local distribution can further adjust the economic structure and productivity, enhance the economic strength and create the material conditions for people’s material and cultural life. Therefore, we regard fixed asset investment as an input indicator.

Gross domestic product (GDP) refers to the final outcome of all resident units of a country (or region) in a certain period of production. In the views of product forms, GDP is the summation of end use of goods and services worth and the value of net exports of goods and services all resident units in a certain period of time. GDP is also the most direct reflection of the energy consumption. Therefore, we regard GDP as an output indicator.

The per capita disposable income refers to the balance amount of taxes and non-commercial costs, including personal income tax, death tax, gift tax, etc., to pay the government. The indicator measures not only the changes in the living standard of country’s nationals, but also is a decisive factor in consumer spending. Therefore, we regard the per capita disposable income as an output indicator.

Average temperature means the arithmetic mean of the temperature value of various observations in a certain period of time; precipitation means the cumulate depth in the horizontal plane, without evaporation, infiltration and loss of land from the sky to the ground on the liquid or solid (thawed) water; sunshine hours refers to the radiation intensity more than or equal to the length of time of 120 W/m2 from the sun daily in the plane perpendicular; the average wind velocity means the average wind velocity observed several times in a certain period of time; the average air pressure means the average value of the pressure observed several times in a certain period of time.

Average air temperature, precipitation, sunshine hours, average wind velocity and average pressure belong to the short-term climatic factors. Short-term climatic factors refer to the short-term climatic reasons or conditions affecting the development and change of other things. The focus of this study considers the short-term climatic factors as input variables of a climatic resource and assesses the impact of economic development. Therefore, we regard short-term climatic factors as input indicators.

In order to improve the analysis effect on short-term climatic factors, annual average air temperature anomaly, annual precipitation anomaly, annual sunshine hours anomaly, annual average wind velocity anomaly and annual average pressure anomaly are regarded as input variables and calculated using Eq. (7). The formulas of other meteorological factors’ time series anomaly have a similar way. In particular, an anomaly refers to the absolute value of difference between a numerical value and the mean value of a series of values.

The annual average temperature anomaly is calculated by:

$$ \Updelta t_{i} = \left| {t_{i} - \overline{t} } \right| $$

(7)

where value $\Updelta t_{i}$ represents the annual average temperature anomaly; value $t_{i}$ the average temperature of the $i$th year; $\overline{t} = \frac{1}{n}\sum {t_{i} }$ the mean value of the average temperature of $n$ years. (Suppose that the time period of a time series is $n$).

3.2 Establish DEA model

According to Sect. 3.1, the input indicators and the output indicators are transformed into the input variables and output variables, respectively.

• 1. The input variables: total energy consumption (million tons of coal equivalent), fixed asset investment (a hundred million RMB yuan), annual average air temperature anomaly, annual precipitation anomaly, annual sunshine hours anomaly, annual average wind velocity anomaly and annual average pressure anomaly.

• 2. The output indicators: GDP (a hundred million RMB yuan) and per capita disposable income (RMB yuan).

Using the input–output variables mentioned above, the DEA models with 31 DMUs from 1980 (DMU ₁ ) to 2010 (DMU ₃₁ ) are established, where each year with different input–output variables is viewed as a DMU.

The solutions and the optimal objection values of the DEA models of 31 DMUs (31-DMUs-DEA) are shown in Table 2 (note: The 31 different numbers segment 31 different DMUs, and “i” stands for $S_{1}^{ - }$, “ii” stands for $S_{2}^{ - }$, “iii” stands for $S_{3}^{ - }$, “iv” stands for $S_{4}^{ - }$, “v” stands for $S_{5}^{ - }$, “vi” stands for $S_{6}^{ - }$, “vii” stands for $S_{7}^{ - }$, “viii” stands for $S_{1}^{ + }$, and “ix” stands for $S_{2}^{ + }$).

Table 2 The input–output parameter results of 31 DMUs in Beijing city

In light of DEA theory, Table 2 indicates that the DMUs are weakly efficient in the year of 1980, 1981, 1982, 1988, 1989,1990, 1991, 1992, 1993,1996,1997, 1999, 2000, 2001, 2002, 2003, 2004, 2005, 2008, 2009 and 2010, and the DMUs are inefficient in the year of 1983, 1984, 1985, 1986, 1987, 1994, 1995, 1998, 2006 and 2007.

Next, effective technology and the validity of the scale of 31 DMUs are concluded according to the results of input and output parameters of 31 DEA models in Table 2 (as shown in Table 3).

Table 3 The results of technical efficiency and scale efficiency of 31 DEA DMUs in Beijing city

In light of DEA theory, Table 3 indicates that the DMUs in 1980, 1981, 1982, 1988, 1989, 1990, 1991, 1992, 1993, 1996, 1997, 1999, 2000, 2001, 2002, 2003, 2004, 2005, 2008, 2009 and 2010 are both technical efficiency and constant return to scale efficiency, while the DMUs in 1983 and 2007 are increasing returns to scale but technical inefficiency, and the DMUs in 1984, 1985,1986,1987,1994,1995,1998 and 2006 are decreasing returns to scale but technical inefficiency.

In the following, we will improve the inefficient DEA into efficient DMUs using Eqs. (6) (as shown in Table 4).

Table 4 The improvement results of inefficient DEA

Table 4 shows that the DMUs with inefficient DEA can be improved into efficient DEA. Since 1980, Beijing city has consumed a large quantity of energy and caused tremendous effect to environment in the process of Beijing city’s economic development. The view can be seen from the amount of total energy consumption saved and fixed asset investment saved. For example, in 1987, in order to make the energy and economic development of input–output situation to achieve to return to scale efficiency, the savings of total energy consumption is 6.0247 million tons of standard coal and the savings of total fixed asset investment is 31.41 hundreds of millions RMB yuan in Beijing city. The other DMUs with inefficient DEA are similarly analyzed.

In summary, the input–output parameter results of the 31-DMUs-DEA models show that, when short-term climatic factors such as average temperature, precipitation and sunshine hours are considered as the input variables of economic development, most of the DMUs are weakly DEA efficient. This explains that the short-term climatic factors are reasonable input variables in DEA model. The short-term climatic variables and energy consumption variables both have effect on economic development of Beijing city. It is also shown that the DMUs with efficient DEA have both technical efficiency and returns to scale efficiency. Through the improvement of the DMUs with inefficient DEA, we find that if we were fully aware that energy consumption and economic development of Beijing city are sensitive to short-term weather conditions and take corresponding energy-saving measures, then energy–economic development of Beijing city would achieve a benign development.

Moreover, it is noted that we have observed some characteristics of variation in Beijing city’s short-term climatic time series data from 1980 to 2010. For example, the largest value (extreme point) of annual precipitation anomaly time series occurs in 1994, and the smallest value in 1999. The largest and smallest values of annual average temperature anomaly time series occur in 1985 simultaneously. The largest and smallest values of annual average sunshine hours anomaly time series occur in 2005 simultaneously. The year of extreme point is the same as the year of the DMUs with inefficient DEA. Therefore, we sufficiently confirm that Beijing city’s energy consumption and economic development have a strong sensitivity to short-term weather conditions since 1980 basing on the results of DEA models (result of the calculation) and data at extreme point (objective data). As far as effective economic development is concerned, the effective activation and utilization of extreme weather conditions is a question worthy of consideration.

4 Conclusion

In this paper, total energy consumption, fixed asset investment, average temperature, precipitation, sunshine hours, average wind velocity and the average pressure being employed as the input variables, and GDP and per capita disposable income being employed as the output variables, we established DEA model based on the time series data in Beijing city from 1980 to 2010 and analyzed the input–output efficiency of DEA of 31 DMUs under the influence of the short-term climatic factors. Generally, it is confirmed that energy consumption and economic growth conditions have strong sensitivity to the short-term climate factors. In other words, the short-term climatic factors have impacts on energy consumption and economic growth of Beijing city since 1980. The specific conclusions and recommendations are as follows:

• 1. The DMUs of 1980, 1981, 1982, 1988, 1989, 1990, 1991, 1992, 1993, 1996, 1997, 1999, 2000, 2001, 2002, 2003, 2004, 2005, 2008, 2009 and 2010 are weakly efficient. This shows that short-term climatic factors have significant influence on the economic development in most time. Meanwhile, according to the efficient analysis of DEA model, it is verified that these DMUs mentioned above all have technical efficiency and constant return to scale.

• 2. In light of efficient analysis of DEA model, it is found that the DMUs of 1983 and 1987 are increasing returns to scale but not technically efficient and the DMUs of 1984, 1985, 1986, 1987, 1994, 1995, 1998, 2006 and 2007 are decreasing returns to scale but not technically efficient. After further improving the above inefficient DMUs, it is discovered that if the amount of energy consumption and fixed asset investment were appropriately controlled, and if the sensitivity of Beijing city’s energy consumption and economic development to short-term climatic factors was sufficiently to realize, then the input–output of Beijing city’s energy and economy would achieve a benign development.

• 3. Observing the change of short-term climatic factors in Beijing city since 1980, it is found that the year of extreme point is the same as the year of the DMUs with inefficient DEA. It is further confirmed that Beijing city’s energy consumption and economic development have strong sensitivity to short-term climatic factors. As far as effective economic development is concerned, the reasonable employing of extreme climatic conditions is a question worthy of consideration. This study can provide effective basis for the scientific and reasonable arrangement of Beijing city’s short-term climatic resources and energy–economic development.