Introduction

In a mining routine, assessing the uncertainty in the characterization of mineral resources is a fundamental step for risk assessment when planning the exploitation of reserves, mainly because it involves modeling complex and heterogeneous geological environments from highly sparse data (Wellmann and Caumon 2018). The characterization of mineral resources involves defining the mineral deposit geometry and the boundaries of ore types before performing the spatial characterization of the metal grades within the spatial domains of each ore type.

Geostatistical methods of stochastic simulation have been used as a tool for modeling the spatial distribution of geological domains and further assessing the spatial uncertainties. Their stochastic approach allows the generation of several different and yet equiprobable realizations, all honoring the information provided by the data (conditioning step) and preserving the variance in the data. Sequential indicator simulation (SIS) (Alabert 1987) and truncated Gaussian simulation (TGS) (Matheron et al. 1987) are two of the most used geostatistical simulation techniques. In SIS, different ore types are transformed into indicator variables whereas in TGS they are sequentially ordered and converted into a continuous random variable with Gaussian distribution prior to simulation. Both methodologies have some limitations in reproducing complex and non-stationary patterns of some geological structures, especially curvilinear ones (Strebelle 2002; Caers and Zhang 2004), and SIS cannot incorporate topological constraints on the simulated domains (Emery 2007). To handle complex facies patterns, TGS has extended capability to implement multiple-Gaussian random functions (Madani and Emery 2017). Another stochastic simulation algorithm that is an alternative to variogram-based methods is multiple-point statistics (MPS) (Strebelle 2002), which relies on statistics extracted from training images to characterize spatial continuity patterns.

Over the years, several authors implemented SIS, TGS and MPS successfully with improved modifications and applied them to different fields of research (e.g., Soares, 1990; Gómez-Hernández and Srivastava 1990; Goovaerts 1994; Xu 1996; Luis et al., 1997; Dimitrakopoulos 1998; Betzhold and Roth 2000; Armstrong et al. 2003; Juang et al. 2004; Zhang 2008; Al-Mudhafar 2017; Yao et al. 2020; Zhang et al. 2022). However, in a complex geological environment, particularly metallic orebodies, these geostatistical methods for characterizing the spatial distribution and uncertainty of boundaries between different geological domains of interest are not a solution in most situations. Therefore, in the mining routine, the morphology and boundaries of ore types are typically defined manually by geological experts, or, when a large number of samples is available, by using deterministic interpolators conditioned by expert/geological control, such as splines surfaces (Munira et al. 2014) and radial basis functions (Beatson et al. 1999). Manual interpretation has several downsides, namely: (1) subjectivity of interpretation, which depends on an expert’s knowledge and experience; (2) irreproducibility; (3) labor-intensive procedure, which makes model updating difficult; and, (4) the deterministic approach makes it difficult to account for uncertainty.

Recently, (Jordão et al. 2022) showed that generative adversarial networks built with deep convolutional neural networks (CNNs) were able to reproduce successfully manual geological interpretation of a complex ore deposit in the southern region of Portugal. Based on historical data from expert interpretation of identical geological environments, a neural network (NN) was trained and tested and used as predictor in new situations. This approach aimed to mitigate two shortcomings, irreproducibility and labor-intensiveness of manual interpretation, which greatly limit the speed at which geological resources can be updated. However, most CNN applications are not able to measure the confidence of their predictions and the resulting uncertainty. Networks continue to be used as black-box function approximators, mapping a given input to a single classification output, making their decisions less understandable to humans (i.e., they are often hard to justify or explain) (Tran, et al. 2022). Moreover, deep learning is often criticized for its lack of robustness (i.e., lack of accuracy under distribution shift) (Tran, et al. 2022), model interpretability (Lipton 2016) and reliable confidence estimates (Guo et al. 2017), which are critical prerequisites for applications in high-risk fields such as the mining industry.

In recent years, uncertainty quantification in deep learning has received a great deal of attention. As a result, several approaches have been proposed (Abdar et al. 2021; Gawlikowski,, et al. 2021). Some methods are based on training an ensemble of NNs (Lakshminarayanan et al. 2017) while others focus on variational inference (Gal and Ghahramani 2016; Jospin et al. 2022). In this paper, we use deep variational inference to assess the two types of uncertainty in Bayesian modeling (Hüllermeier and Waegeman 2021): epistemic uncertainty and aleatoric uncertainty. Epistemic uncertainty, also known as model uncertainty, refers to uncertainty caused by lack of knowledge about the true data-generating function (more precisely, the model parameters uncertainty). Epistemic uncertainty can be reduced with additional information. As in traditional methods used to estimate mineral resources—kriging, stochastic simulation (Journel 1974; Journel and Huijbregts 1978; Journel and Kyriakidis 2004)—epistemic uncertainty can be caused, for example, by the uncertainty of variogram parameters. Aleatoric uncertainty is irreducible and captures noise that is inherently present in the data. In subsurface modeling, the aleatoric uncertainty is closer to the uncertainty regarding the reality one wishes to predict than the model uncertainty (epistemic). Aleatoric uncertainty is a measure of heterogeneity of the real phenomenon one wishes to predict, as well as the lack of knowledge about it (lack of samples or observations).

Monte Carlo dropout networks (MCDNs) are a widely used architecture for uncertainty quantification (Gal and Ghahramani 2016). Dropout is a regularization technique used to avoid overfitting. Dropout works by randomly switching off some neurons of a deep NN (Fig. 1). In the training phase, a dropout probability (DP) is set for each layer, following a Bernoulli distribution (Srivastava et al. 2014). Gal and Ghahramani (2016) showed that using dropout during inference can be interpreted as a Bayesian approximation of a Gaussian process. MCDNs have important advantages, namely: (1) They can be implemented easily with minor modifications to a NN architecture; (2) they do not require additional NN parameters, and thus do not increase computational burden; and (3) they can be optimized using traditional methods. Therefore, MCDNs have been used in several fields of research (Kendall and Gal 2017; Abdar et al. 2021; Mobiny et al. 2021). In geosciences applications, for example, (Mukhopadhyay and Mallick 2019) proposed a CNN with dropout for seismic facies classification and introduced the concept of predictive entropy to obtain uncertainty maps. Feng et al. (2021) applied the dropout approach to quantify fault segmentation and analyzed aleatoric and epistemic uncertainty. Maldonado-Cruz and Pyrcz (2021) tested the dropout method with a subsurface flow surrogate model and proposed the use of a method known as uncertainty model goodness for improving dropout frequency tuning. Um et al. (2022) quantified uncertainties of CO2 saturation estimates (in a CO2 sequestration and storage process) using the Monte Carlo dropout method and a bootstrap aggregating method.

Figure 1
figure 1

Left: Basic NN with one hidden layer, each weight has a fixed value. Center: Basic NN after applying dropout. Crossed units have been dropped. Right: Bayesian NN each weight is assigned a probability distribution instead of a single value

Full size image

Bayesian NNs (BNNs) are an alternative uncertainty quantification framework (Jospin et al. 2022). They are an extension of NNs in which all parameters—weights and biases—are assigned as a probability distribution instead of a single value or point estimate (Fig. 1). The NN learns the posterior distribution over weights given the training data and the prior distribution. Because computing the Bayesian posteriori is usually an intractable problem, approximate Bayesian inference methods such as variational inference can be used (Abdar et al. 2021; Jospin et al. 2022). In addition to accounting for uncertainty, BNNs are more robust to extrapolation (avoiding overfitting) and can learn from small datasets. However, probabilistic NNs are computationally expensive for large NN models because they require a considerable number of parameters. In MCDNs, only a single point is trained, whereas in BNN, two parameters are estimated for each weight (mean and variance) to represent a Gaussian distribution, doubling the number of parameters to be trained. Gal and Ghahramani (2016), Lakshminarayanan et al. (2017) and Mobiny et al. (2021) found that BNNs are not scalable due to the computational burden and the intractable inference of the posterior model. LaBonte et al. (2019) refuted this finding by developing a BNN applied to the segmentation of 3D computed tomography scans of graphite electrodes and laser-welded metals. They compared BNN and MCDN results and found that BNN uncertainty not only yields more credible confidence intervals than the MCDN but are also computationally feasible.

In a previous study, (Jordão et al. 2022) showed the ability of a generative adversarial network to replicate the extremely time-consuming routine of manual geological interpretation of orebody domains. The method does not intend to reproduce the unknown reality but rather to reproduce the interpretation procedure of one or more experts of a given geological environment. In this study, our aim was to assess the uncertainty of these morphological domains of complex geological environments with high local non-stationarity patterns (e.g., folding, faults and meanders). We explored and compared MCDN and BNN to assess the uncertainty—epistemic and aleatoric—of deep convolutional NN models trained to predict geological domains conditioned to drill-hole samples. The implementation used two-dimensional (2D) vertical sections extracted from an historical three-dimensional (3D) model of interpreted ore type boundaries as reference images and the set of borehole samples as a conditioning starting image. After training, each NN reproduced the interpretation expertise of the geologist by generating multiple realizations for each newly available set of borehole samples. These realizations were combined to create a probability map for each ore type class and from it we computed and evaluated the mean prediction and predictive uncertainty. The application example was a real case study of several ore types in a polymetallic sulfide orebody in the south of Portugal. This paper presents the development and implementation of methodologies to achieve a real-time framework for updating resources in mining operations. The proposed framework addresses the disadvantages of manual geological interpretation procedure, namely, time-consuming, resource intensive and unable to provide a measure of uncertainty.

Methods

Architectures

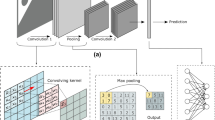
In the application example here, each deep learning model, MCDN and BNN, was implemented with a U-Net architecture (Fig. 2). The framework is an encoder/decoder with skip connections added between the encoding layers and the corresponding decoding layers. The encoder performed down-sampling through six blocks of layers to the bottleneck layer (convolutional layer (kernel 4 × 4, stride 2 × 2) + batch normalization + leaky ReLU (α = 0.2)—except for the first layer, where batch normalization was not used). Next, the decoder had seven blocks of layers (transposed convolutional layer (kernel 4 × 4, stride 2 × 2) + batch normalization + ReLU). The output layer had a transposed convolutional layer (kernel 4 × 4, stride 2 × 2) followed by a softmax activation function. The input was the conditioning image, a 2D image of the drill-hole samples with size of 256 × 256 × 3. The output was a 256 × 256 × 3 pixel image of the geological model conditioned to the drill-hole samples. Each channel represented a different ore type. This U-Net architecture can deal with geological models with more domains by adding channels at the input and output. Nevertheless, the more features and variability of the expected output it should take into account, the more data are needed for training.

Figure 2
figure 2

Architecture of the U-net. Arrows represent the skip connections

Full size image

To capture uncertainty in the MCDN, dropout layers were added after each block of layers (but not after the output layer). Different probabilities of dropout between 0.1 and 0.6 with increment of 0.1 were studied. As dropout minimized overfitting during training and introduced variability in the model’s predictions, each forward pass through the trained network generated different output values. The mean prediction and deviation can be estimated over several model inferences on the same input (Fig. 3). The basic U-Net and the MCDN were optimized by minimizing negative log-likelihood.

Figure 3
figure 3

Flow diagram of both MCDN and BNN approaches to assess spatial uncertainty

Full size image

To assess uncertainty in the BNN, each transposed convolutional layer of the decoder was replaced by an up-sampling layer followed by a probabilistic layer—a convolution layer with probability distributions of the weights. Due to GPU memory limitations, only the convolutional layers of the decoder were replaced by probabilistic layers. A standard Gaussian distribution (zero mean, unit variance) was tested as the prior distribution. Thus, instead of learning point estimate values, it learned the mean and standard deviation of the distributions via backpropagation. These distributions were optimized through iterative training using Bayes’ theorem by backpropagation algorithm, where the proposed method trained an ensemble of networks instead of training a single network, and where the weights of each network were drawn from a shared, learnt probability distribution (Blundell et al. 2015). Flipout gradient estimator was used to implement Bayesian variational inference (Wen et al. 2018). Variational learning finds the parameters \(\theta\) of the distribution \(q\left(\theta \right)\) by minimizing the evidence lower bound (ELBO), thus:

$$F\left(D,\theta \right)=KL\left[ q\left(\theta \right) \| P\left(w\right)\right]-{E}_{q\left(\theta \right)}\left[logP\left(D|w\right)\right],$$
(1)

where \(w\) represents the NN learnable parameters and \(D\) the dataset consisting of \(N\) input–output pairs \(D={\left\{{x}_{n},{y}_{n}\right\}}_{n=1}^{N}\), with inputs \(X={\left\{{x}_{n}\right\}}_{n=1}^{N}\) and targets \(Y={\left\{{y}_{n}\right\}}_{n=1}^{N}\). The first term is the Kullback–Leibler (KL) divergence between the variational distribution \(q\left(\theta \right)\) and the prior \(P\left(w\right)\). The KL divergence measures the complexity of a posterior distribution in relation to the prior distribution. The second term is the likelihood of the parameters given the data, a negative log-likelihood (NLL) that measures the error in the training examples.

The KL divergence should be applied once per epoch (Graves 2011). Moreover, a balance between the KL divergence and the NLL is needed to prevent any of the terms from dominating the loss function. For example, if the value of the KL divergence is an order of magnitude larger than the NLL, the model will converge to a posterior with suboptimal accuracy. In this work, a KL scaling equal to 5000 was used. Jospin et al. (2022) provided a thorough explanation of the optimization process.

The uncertainty quantification procedure was the same as the one used for the MCDN: by sampling the NN multiple times on the same input, spatial uncertainty was quantified by calculating the variability of the ensemble of realizations. The mean geological model prediction and the associated uncertainty for each drill-hole image were generated from 100 realizations to obtain the probability distribution of each class for each pixel (Fig. 3).

All networks were trained using the Adam optimizer (Kingma and Ba 2014) with a batch size of two and an initial learning rate of 0.0002. The probabilistic BNN was implemented using TensorFlow probability (Abadi et al. 2015). Early stopping was used, and the training phase automatically terminated when the performance in the validation loss ceased to improve during five consecutive epochs. All methods were implemented using Keras with TensorFlow (Abadi et al. 2015) and tested on a GeForce GTX 1070 (8 GB of GDDR5). The BNN had 68,314,470 trainable parameters, while the MCDN had 41,829,507.

Mean Prediction and Uncertainty Model

The NNs were trained to generate geological models conditioned to the drill-hole samples. The output of the networks consisted of a softmax layer that applied the softmax function to the channel dimension (i.e., each channel represents one ore type class). The size of the output image was 256 × 256 × 3, with the channels representing the three ore type classes. After training, the result of \(N\) forward passed through the model on the same input can be computed, and the mean prediction and predictive uncertainty of the ensemble of realizations can be estimated. Each geological model of the ensemble represented a valid and equiprobable model sample.

The mean prediction modeling followed this sequence. First, for each generated image, the probabilities given by the softmax function were converted into a one-hot encoded class by assigning the class with the highest probability of all classes: \(i=1,\dots ,n\). Next, a probability map \(\left(P\right)\) of the ensemble was created by calculating the pixelwise average of the \(N\) geological model samples (i). The probability map represented the probability that a pixel is in a given class. In the probability maps, \({P}_{x,i}\) for pixel \(x\) and class \(i\), the average of all images is given by:

$${P}_{x,i}=\frac{1}{N}{\sum }_{k}^{N}{d}_{x,i}^{k},$$
(2)

where \({d}_{x,i}^{k}\) is the value assigned to pixel \(x\) in class \(i\), which has the highest probability of all classes in the \(kth\) image sample. In a multi-class classification problem, in which each class \(i=1,\dots ,n\) is represented by a channel (one-hot encoded), one obtains \(n\) probability maps, one for each channel (oretype).

The mean prediction model can be obtained from the probability map \({P}_{x,i}\) , \(i=1, \dots , n\) by assigning each pixel to the class with the largest predicted probability of all classes. Based on \({P}_{x,i}\), several metrics can be used to measure uncertainty. For example, the uncertainty map for each class can be obtained by taking the variance \(var(i,x)={ P}_{x,i} (1- { P}_{x,i})\). Another measure of uncertainty for probability distributions is the Shannon entropy, which captures the shape of a distribution, and hence the uncertainty of the outcome of a random variable. Therefore, it is more suitable for capturing aleatoric uncertainty (Hüllermeier and Waegeman 2021). The Shannon entropy for a probability distribution \({P}_{x,i}\) with \(n\) classes is defined as follows:

$$H\left({P}_{x}\right)=-\sum_{i=1}^{n}{P}_{x,i}{\mathrm{log}}_{2}{(P}_{x,i}).$$
(3)

The \(H\left({P}_{x}\right)\) takes values between zero and \(n\). A \(H\left({P}_{x}\right)\) value of \(n\) means a highly uncertain prediction for equally likely outcomes of \({P}_{x,i}=1/n\) for all classes. A \(H\left({P}_{x}\right)\) value close to zero means a highly certain prediction; taking the value of zero if, for any class, \({P}_{x,i}=1\).

Performance Evaluation Metrics

The following metrics were used to evaluate the accuracy of predictions and predictive uncertainty quality on the test dataset.

The prediction performance of each NN was assessed using pixel accuracy (\(PA\)) and mean intersection over union (mean \(IoU\)) metrics (Jaccard 1901). PA is the percentage of pixels that are classified correctly. \(IoU\) quantifies the percent overlap between the target and the prediction, divided by the area of union between them, thus:

$$\mathrm{mean} IoU=\frac{1}{n}{\sum }_{i}^{n}\frac{|{G}_{i}\cap {R}_{i}|}{|{G}_{i}\cup {R}_{i}|}.$$
(4)

where \(G\) and \(R\) are the prediction and target areas of each class \(i\) for \(i,\dots ,n\). The mean \(IoU\) of an image is calculated by taking the \(IoU\) of each class and averaging them.

We also computed uncertainty accuracy (UA), as proposed by Mobiny et al. (2021). The UA in a pixel level is measured as the ratio of correct–certain \({N}_{cc}\) (i.e., correct prediction and low uncertainty; incorrect–uncertain \({N}_{iu}\)(i.e., incorrect prediction and high uncertainty); correct–uncertain \({N}_{cu}\) (i.e., correct prediction but high uncertainty); and incorrect–certain \({N}_{ic}\) (i.e., wrong prediction but low uncertainty). The UA metric can be measured as the ratio of the desired cases over all possible cases (Mobiny et al. 2021), thus:

$$UA=\frac{{N}_{cc}+{N}_{iu}}{{N}_{cc}+{N}_{iu}+{N}_{cu}+{N}_{ic}}.$$
(5)

Additionally, the accuracy/confidence relationship was also evaluated through a calibration curve (also called a reliability plot) and the expected calibration error (ECE). Deep NNs are often not calibrated, which means that the confidence estimate (predictive uncertainty) does not represent a true probability (the observed probability of correctness) (Guo et al. 2017). One way to check if a model is calibrated is to draw a reliability plot. If the model is calibrated, the confidence should equal the accuracy. ECE is the weighted average of the difference between the fraction of correct predictions within a bin (accuracy) and the mean of the probabilities (confidence) within the same bin (Guo et al. 2017). The ECE metric can be used to measure the calibration level. Lower ECE scores correspond to better calibrated predictions. For a multi-class model, the predicted label and the confidence are for the highest-scoring class.

$$ECE={\sum }_{b=1}^{B}\frac{{n}_{b}}{N}\left|accuracy(b)-confidence(b)\right|,$$
(6)

where \(N\) is the total number of samples, \({n}_{b}\) is the number of predictions in bin \(b\), and \(B\) is the number of bins; \(accuracy(b)\) and \(confidence(b)\) are the accuracy and confidence of the predictions of bin \(b\), respectively.

Real Case Study: Copper Sulfide Deposit

The dataset was drawn from a real volcanogenic sulfide deposit located in the south of Portugal. The database was established using an existing historical 3D model of orebody domains drawn via geological interpretation and the drill-hole samples used by the geologists as conditioning data (Figs. 4 and 5). The geological model of the sulfide deposit included two ore types—stockwork (STWK) and massive sulfide (MSV)—and the barren rock (BR). In the study area, the MSV was located within the STWK orebody. The STWK was wider and its contact with the BR was more continuous and homogeneous when compared to the boundaries between the MSV and STWK (Figs. 4 and 5).

Figure 4
figure 4

Ore type individual view. Left: Stockwork in gray color. Right: Massive in yellow color. Barren rock not represented

Full size image
Figure 5
figure 5

Left: Ore type model (barren rock not represented). Right: Drill-hole lithology

Full size image

The three classes were encoded using one-hot encoded scheme. One-hot encoding creates new (binary) channels, which indicate the presence of each possible class from the original data. The data were composed of pair images from drill-hole samples and the corresponding geological model (Fig. 6). The pair images were created by taking 2D parallel sections along the main axis of the 3D geological model—the direction of highest spatial continuity—and the conditioning drill-hole data falling into each cross section. For prediction purposes, the drill-hole samples, as conditioning data, functioned as input variables, and the geological model cross sections were the output of the predicted model. The drill-hole samples and the geological orebodies 2D cross sections were represented by images with 256 × 256 × 3 pixel size (the three channels representing each class—STWK, MSV and BR).

Figure 6
figure 6

Examples of paired images of geological models and drill-hole lithology samples

Full size image

The models were trained with 613 paired images of the drill-hole samples and the geological models were conditioned to those drill-hole samples, which were drawn by the expert geologist (Figs. 6 and 7). The validation and test datasets contained 100 and 154 paired images, respectively.

Figure 7
figure 7

Dataset used in this study: a drill-hole lithology and two examples of 2D vertical sections taken to establish the drill-hole database (black dotted lines); b ore type model (barren rock not represented and two examples of 2D vertical sections taken to establish the geological model database—red dotted lines) (source: (Jordão et al. 2022)

Full size image

Results

The PA and uncertainty estimate performance results obtained on the test set, for each model, were evaluated and compared per the task of generating geological models conditioned to the drill-hole samples.

Prediction Performances and Uncertainty Quality of MCDNs and BNNs

The MCDN models were evaluated for different DPs, with DPs varying from 0.1 to 0.6. Table 1 shows the PA, UA, and calibration performance of the six MCDNs tested, where the bold fonts indicate those with the best performance.

Table 1 Pixel accuracy (PA), mean intersection over union (mean IoU), uncertainty accuracy (UA) and expected confidence error (ECE) evaluation of geological models conditioned to the drill-hole samples with MCDN of different dropout probabilities (DPs)
Full size table

In terms of PA, the models with DPs of 0.3–0.5 showed the best results with 0.98 and 0.93 for PA and mean IoU metrics, respectively. The MCDN with DP = 0.4 showed the best result based on UA and ECE of the models. Regarding calibration, all MCDNs were reasonably calibrated (Fig. 8). In the confidence interval between 0.8 and 0.9, all models tended to be overconfident in their predictions (i.e., confidence > accuracy). The best calibrated MCDN was for DP = 0.6 with ECE of 0.003.

Figure 8
figure 8

MCDNs reliability plot of the model’s probability map on the test set data. The dash line represents a perfect calibrated model where accuracy equals the confidence

Full size image

Next, the BNN and the MCDN (DR = 0.4) were compared. In Figure 9, the loss values on both training and validation data sets are shown. For MCDN, the number of epochs used in training was 128, the minimum values of the loss (reached at the end of the training) were 0.028 and 0.043 for the training and validation datasets, respectively. The loss values had a sharp decrease from the beginning of the training until the 10th epoch. For BNN, the loss was composed of two terms, the NLL (as in MCDN) and the KL divergence. These two terms are plotted separately in Figure 9. The number of epochs used for training was 165, the minimum of NLL losses were 0.538 and 0.565 for the training and validation datasets, respectively. The minimum KL divergence was 0.241 for both the training and validation datasets. During training, NLL and the KL divergence values exhibited a very similar behavior. The NLL losses had a sharp decrease from the beginning of the training until the 55th epoch. Figures 10 and 11 illustrate the convergence of the BNN variational probability distribution of the weights \(q\left(\theta \right)\) through training iterations (plots for epochs 2 and 164 are shown). At the beginning, priors dominated the distributions since that all are similar. In the end, the posteriors differed as driven by the data.

Figure 9
figure 9

Loss of MCDN (DP = 0.4) (left) and BNN (right) during training iterations

Full size image
Figure 10
figure 10

Variational probability distribution of the weights (mean and standard deviation) of two probability layers of the decoder at epoch 2

Full size image
Figure 11
figure 11

Variational probability distribution of the weights (mean and standard deviation) of two probability layers of the decoder at epoch 164

Full size image

The prediction and uncertainty estimates obtained from the MCDN (DP = 0.4) and the BNN were compared (Table 2, Fig. 12). The PA results were also compared to the ones obtained from a deterministic U-Net (without dropout). MCDN (DP = 0.4) predictions had the best results in terms of PA, and an even better performance when compared to the traditional U-Net. Adding dropout layers increased the performance of the NNs because it prevented the co-adaption of neurons during training, making the model more robust. Complex co-adaptations can lead to overfitting because they do not generalize to unseen data (Hinton, et al. 2012).

Table 2 Pixel accuracy (PA), mean intersection over union (mean IoU) and uncertainty accuracy (UA) evaluation of geological models conditioned to the drill-hole samples from the test set using different methods
Full size table
Figure 12
figure 12

Reliability plot (top) and confidence distribution (bottom) for the BNN and the MCDN with DP = 0.4

Full size image

UA and calibration were quantified (Table 2) using the proposed metrics (Eqs. 5 and 6). MCDN (DP = 0.4) predictions had the highest UA and the lowest ECE. BNN predictions were also reasonably calibrated but were overconfident (i.e., confidence > accuracy) in the confidence interval between 0.8 and 0.9. For both models, more than 90% of the predictions had a prediction confidence higher than 0.9 (Fig. 12) (95% for the MCDN and 92% for the BNN). Overall, the different methods obtained similar results in terms of PA, except for the mean IoU value for the BNN. Mean IoU was calculated for the three ore types—BR, STWK and MSV (Table 3). The highest difference between mean IoU was caused mainly by the greater difficulty in defining the boundaries of the MSV ore type (Table 3).

Table 3 Intersection over union by class of geological models conditioned to the drill-hole samples from the test set using different methods
Full size table

Figures 13 and 14 show two examples of different cross sections with the geological model targets, the drill-hole samples (input), the geological models conditioned to drill-hole samples, the results from the MCDN and BNN frameworks, and the corresponding error maps. In the first example (Fig. 13), the spatial distribution of ore types was more homogeneous and continuous than the one shown in the second example (Fig. 14). In both examples (Figs. 13 and 14), the ore type boundaries produced by the MCDN model were highly detailed, even without drilling information, because the model reproduced the way the interpreter/geologist modeled similar scenarios, which was consistent with the higher mean IoU for the MCDN (Table 2). The ore type boundaries produced by the BNN were smoother than the ones produced by the MCDN, and, in general, the BNN predictions underestimated the size of ore type domains, especially the MSV, although the BNN predictions were conceptually closer to a least squares interpolation model in relation to the unknown reality.

Figure 13
figure 13

Left: Pair sample from the test set composed of the target image and the drill-hole samples of the same section (un-sampled locations represented in black). Right: prediction and error results for the BNN (mean IoU = 0.89) (bottom) and the MCDN (mean IoU = 0.96) (top)

Full size image
Figure 14
figure 14

Left: Pair sample from the test set composed of the target image and the drill-hole samples of the same section (un-sampled locations represented in black). Right: mean prediction and error results for the BNN (mean IoU = 0.81) (bottom) and the MCDN (mean IoU = 0.89) (top)

Full size image

Uncertainty in Geological Interpretation and Associated with Geological Reality

The main goal of this work was to measure and compare the uncertainty obtained with different models, MCDN and BNN, and to evaluate qualitatively the results for the two types of uncertainty defined earlier—uncertainty in geological interpretation and uncertainty associated with geological reality.

Figures 15 and 16 show two examples of cross sections with the geological model targets, the results of the geological models conditioned to drill-hole samples from the MCDN and BNN frameworks, the error map, and the uncertainty using the Shannon entropy metric (Eq. 3). The spatial distribution of the ore types in the first example (Fig. 15) was more homogeneous and continuous than the one in the second example (Fig. 16). In both examples, the MCDN predictions performed better in terms of the ability to mimic the process of manual interpretation of the spatial domains of different ore types by an expert geologist, which is consistent with the higher mean IoU for the MCDN (Table 2). The ore type boundaries produced by the BNN were smoother than the ones produced by the MCDN and, generally, BNN predictions underestimated the size of ore type domains, especially the MSV. Nevertheless, the BNN better captured the continuity of the ore type boundaries.

Figure 15
figure 15

Top: Pair sample from the test set composed of the target image and the drill-hole samples of the same section (un-sampled locations represented in black). Mean prediction, error, and uncertainty results for the MCDN (middle) and the BNN (bottom)

Full size image
Figure 16
figure 16

Top: Pair sample from the test set composed of the target image and the drill-hole samples of the same section (un-sampled locations represented in black). Mean prediction, error, and uncertainty results for the MCDN (middle) and the BNN (bottom)

Full size image

Therefore, the most likely predicted MCDN model, shows the ore type boundaries in great detail, even without drilling information, because it reproduces the way the interpreter/geologist modeled similar scenarios, while the most likely predicted BNN model (Figs. 7b and 8b) produced smoother ore type boundaries, and was conceptually closer to a least squares interpolation model, in relation to the unknown reality.

Looking at the uncertainty maps, the MCDN interpreter model had very low uncertainty in both examples (Figs. 15 and 16) because the NN “learned” quite well with the historical dataset, i.e., how the geologist interpreted the ore type boundaries in similar situations of conditioning data. The uncertainty was highest in areas where the interpreter/geologist had more difficulty delineating the boundaries of geological bodies. This is known as geological interpretation uncertainty, or epistemic uncertainty.

The BNN uncertainty regarding the geological reality (Figs. 15 and 16) was higher and more pronounced in the more discontinuous contacts, where the conditioning data indicate local spatial heterogeneity of the ore types boundaries. The uncertainty bandwidth was wider for the MSV ore type, which was the least frequent, most complex, and most heterogeneous class.

Figure 17 shows two zoomed-in portions of the uncertainty maps in Figure 16. Both examples were contact areas between the STWK and the BR. As expected, wider uncertainty bands were visible where the limits were more complex and heterogeneous. This was less visible in the MCDN, as the uncertainty for both examples showed equal dispersion and intensity, which indicated that the geological interpretation was identical to similar past scenarios, i.e., the training data. Moreover, in certain cases, the uncertainty bands seemed pixelated. However, the uncertainty bands produced by the BNN were wider and more continuous than the ones produced by the MCDN, and a gradient of uncertainty values was visible.

Figure 17
figure 17

Zoomed-in portions of the uncertainty maps shown in Figure 16

Full size image

Final Remarks

Characterization of an orebody model is a crucial step in mining operations because it is the basis for the estimation of resources and for follow-up mine planning decisions. Today, modeling orebodies in complex geological environments is still a challenge because it implies expert interpretation. This process requires experienced geologists, is time-consuming, is susceptible to person-to-person variability, and greatly limits the speed at which mineral resources are updated.

A recent study demonstrated the successful application of deep learning techniques for geological modeling (Jordão et al. 2022). It showed that CNNs can reproduce the interpretation of ore type morphology given by one or more geologists when trained with historical versions of the geological model. However, given the highly sparse information used to build geological models and their complexity and heterogeneity, it is important to quantify uncertainty and to propagate and accumulate it in the resource estimation and mine planning workflow.

In this work, a MCDN and a BNN were used to measure uncertainty in the task of generating geological models conditioned to drill-hole samples. In the MCDN, dropout was used to obtain the distribution of predictions. In the BNN, the weights were modeled with a Gaussian distribution and the posterior was obtained using variational inference. These models capture different types of uncertainty—the uncertainty of the interpretation model (MCDN) and the uncertainty of the geological model (BNN).

On the one hand, the MCDN method essentially provides a measure of the uncertainty of a model, in this case, the geological interpretation model, where the greatest uncertainty was in areas where the interpreter/geologist had more difficulty delineating the boundaries of geological bodies. The neural net learned from the historical data in cases where the interpretation was less precise, no matter if it was accurate regarding the reality, and reproduced this uncertainty in the model’s predictions. The uncertainty quantification method of the MCDN is a measurement of the model uncertainty rather than the uncertainty regarding the unknown reality. The dropout approach follows a similar principle to the resampling methods of nonparametric statistics, such as bootstrapping (Efron 1979).

On the other hand, the BNN can capture the uncertainty regarding the unknown boundaries of the ore types by modeling the relationship between dependent and independent variables with probability distributions. By replacing the weights of a classical NN with probability distribution functions, the BNN proposes a similar approach of training an ensemble of NNs around these probability distributions. The uncertainty resulting from this algorithm is caused by the probability distributions of the weights (layers of the NN) and, consequently, from the resulting ore type models conditioned to the existing training data (drill holes and geological images of the ore types).

The model uncertainty results obtained with the MCDN seem to be highly coherent with the data used for training. The BNN method showed very promising results for the assessment of the uncertainty of ore type boundaries created by a deep NN.

Finally, in a geological model routine for resources evaluation, the uncertainty of the ore type boundaries obtained by the proposed method must be used to characterize the uncertainty of the posterior metal grades inside each ore type. This presents a challenge, and future studies could address how to integrate the geometrical boundaries uncertainty in the spatial simulation of the metal grades uncertainty.

Conclusions

This work aimed to create uncertainty maps that represent the confidence of the predictions (the models’ uncertainty) but also capture the uncertainty regarding the unknown reality. The uncertainty of the ore type boundaries depends on the ore type frequency, the complexity of the geometry and the heterogeneity of the boundaries, and the amount of information available (drill-hole samples) around the boundaries. These are the same sources of uncertainty which the geologist accounts for when building an orebody model. Thus, it is expected that the models will produce wider uncertainty bands where the limits are more complex and heterogeneous. For the MCDN, these bands are not visible, and the uncertainty maps show equal dispersion and intensity values regardless of the complexity of the boundaries and the conditioning data. The MCDN uncertainty maps reflect mainly the geological interpretation uncertainty. However, the BNN uncertainty bands are visible depending on ore type frequency, complexity and heterogeneity. The BNN underestimates the size of the ore type domains but the correct limits are within the wide uncertainty bands. The BNN is able to better represent the uncertainty regarding the unknown reality. This work presents the development and implementation of methodologies to achieve a real-time framework for updating resources in mining operations. The promising results show a framework capable of producing fast and robust estimation and uncertainty assessment of ore type boundaries in complex geological models.