Model predictive control for path tracking in cable driven parallel robots with flexible cables: collocated vs. noncollocated control

Abstract

This paper proposes a novel control scheme for precise path tracking control in cable driven parallel robots (CDPRs) with axially-flexible cables, with particular focus to the challenging case of cable suspended parallel robots (CSPRs). To handle model nonlinearities while ensuring small computational effort, a controller made by two sequential control actions is developed. The first term is a position-dependent, model predictive control (MPC) with embedded integrator to compute the optimal cable tensions ensuring accurate path tracking and fulfilling the feasibility constraints; bounds on the feasible tensions are also included. The second control term transforms the optimal tensions into the commanded motor torques, and hence currents, that are evaluated through the kinetostatic model of the electric motors used for winding and unwinding the cables. Control design is performed through the robot dynamics model, formulated with the assumption of rigid cables. Moreover, the proposed control strategy is presented in two different architectures, collocated control and noncollocated control. Flexibility is handled by penalizing large tension variations in the cost function adopted in the controller design, plus some hard constraints on the maximum tension derivatives. These features, together with the embedding of the integrator within the MPC formulation, ensure smooth control tensions that allow handling the axial flexibility of the cables, although it is not explicitly considered in the controller design.

To assess the performances of the proposed control algorithm, a kinematically-determined robot with a suspended, lumped end-effector is simulated by also adopting very flexible cables. Additionally, a simplified dynamic model of the electrical dynamics and the sensor quantization are included to provide a realistic representation of the real environments. The results, together with the fair comparison with a benchmark, corroborate the effectiveness of the proposed approach, its robustness, and its feasibility in real-time controllers due to the wise reduction of the computational effort.

1 Introduction

1.1 State of the art and paper motivations

Cable driven parallel robots (CDPRs) have been attracting an even greater attention of researchers in the fields of robotics and multibody system dynamics because of their benefits that include large workspaces and large payloads, which result in a lightweight and cheap design [1–3]. On the other hand, motion planning control of such robots is challenging since cables can pull but not push the end-effector, leading to a unilateral actuation (i.e., just tensile cable forces can be exerted). This limitation is sometimes overcome at the design stage through cable redundancy or by placing cables below the moving end-effector, thus resulting in a more expensive construction. A more ambitious approach is developing cable suspended parallel robots (CSPRs), i.e., when all cables lie above the moving end-effector without redundant actuation forces: this is the occurrence investigated in this paper.

In CDPRs, and even more in CSPRs, ensuring positive cable tensions along the path, therefore, relies on advanced motion planning and control techniques. Optimal motion planning has been widely investigated by designing trajectories that a-priori ensure positive and bounded cable tensions in an open-loop manner, by exploiting the robot dynamic model, and in the presence of some boundary conditions (e.g., [1, 4] and the references therein). As far as closed-loop control is concerned, standard industrial controllers, such as PID, have been mainly applied to this kind of robotic systems in the last decades [5, 6]. The drawback of such standard controllers is that the positiveness constraints on the cable tensions, as well as bounds on the feasible maximum tensions, cannot be embedded in the control design and, hence, a-posteriori verification or control saturation should be adopted. However, a-posteriori saturating in the presence of integral control is often ineffective and might lead to relevant overshoot due to windup. Thus, these controllers are effective in the presence of optimized trajectories.

The recent advances in the field of motion control of multibody systems suggest that CDPRs can benefit from some advanced control techniques to improve their performances. In this paper, precise path tracking control in a CSPR is solved through a control strategy made by two control actions, which exploits the fundamental concepts of model predictive control (MPC). Indeed, among the several model-based control techniques used for multibody systems, MPC has several features that make it very attractive for CDPRs in general and, in particular, for the more challenging case of CSPRs.

The underlying idea of MPC is to compute the optimal control forces by solving an optimal control problem defined through a cost function. The optimization problem over the future control variables is solved at each time step by predicting the future system states and outputs over a receding horizon. Hence, MPC provides an optimal sequence of the control input in accordance with some metrics. Prediction is performed through a first-order representation of the dynamic model and bounds on the control variables can be embedded in the optimization problem. These features make MPC attractive for motion control of multibody systems (see, e.g., [7–9]) and in particular of CDPRs: constraints on input and output variables can be effectively included without requiring a-posteriori saturations.

In the very last years, just a few researchers in the field of CDPRs have applied concepts of MPC [10–15], showing good solutions; as a matter of fact, the greatest efforts have been devoted to ensure positive tensions through optimal motion planning (see, e.g., [1, 16, 17] and the references therein). The idea of MPC has been also adopted to plan dynamic transition trajectories for a fully-actuated cable suspended robot in [18].

1.2 Paper contributions and underlying idea of the control scheme

In this work, a novel control architecture based on MPC is proposed for precise path tracking control in CDPRs by investigating the more challenging case of a fully-actuated, nonredundant robots with suspended configuration. Some preliminary results of this research have been proposed in [19, 20] by applying the controller to an ideal system with rigid cables and by neglecting the presence of the actuator and sensor dynamics. An extension of the control scheme, with an enhanced architecture, is here proposed to cope with a more realistic scenario by also providing a comprehensive approach for the controller design and analysis.

The proposed control scheme is based on two consecutive actions to allow for a simpler implementation and for effectively handling the nonlinearities of the dynamic model with a low computational effort. The first control action is responsible for the evaluation of the optimal cable tensions required to move the end-effector along the desired path by exploiting the nonlinear dynamic model relating the cable tensions and the end-effector coordinates. The MPC algorithm is here exploited and designed by just considering this submodel. The second action of the proposed control scheme consists in the evaluation of the required motor torques leading to the optimal cable tensions commanded by the MPC algorithm by exploiting the inverse dynamic models of the electric motors.

Two different control architectures are considered for the computation of the optimal tensions, depending on the type of measurement adopted for feedback in the MPC. The first approach just exploits the position measurements of the winch motors (and hence the estimated speeds) to estimate the end-effector Cartesian position and speed through the forward kinematic model with rigid cables, leading to a purely collocated control architecture. The second approach assumes that a direct measurement of the end-effector position is available and is, therefore, exploited as the feedback in the MPC. This control approach can be therefore referred as a noncollocated approach. Both architectures are adopted in the case of axially-flexible cables; clearly, in this case the use of a kinematic estimation provides just an approximation of the actual robot end-effector pose.

As far as the motor torque computation is concerned, it is assumed that no cable tension feedback is available, as it is assumed for instance in other papers on motion control of CDPRs [21], thus simplifying the hardware implementation of the feedback scheme.

In both the collocated scheme and the noncollocated one, the model of the system flexibility is not directly considered. Indeed, the MPC design based on just the subsystem made by the end-effector allows computing the optimal sequence of cable tensions regardless of the cable flexibility. This latter is therefore handled by imposing a smooth control action computed by the MPC algorithm to penalize large tension derivatives (and hence avoiding jerky motion) and by constraining them as well. Flexibility of cables is also handled by designing the MPC with adequate stability margins, so that stability and performances are preserved also in the presence of axially-flexible cables and with uncertain parameters.

The idea of designing controllers for flexible systems by means of just simplified model of elasticity, or even by just imposing smooth motion, is often a need in the case of complicated or industrial systems or if computational effort of controller should be kept small, and some recent papers in the field of controlling multibody systems successfully address this issue (see, e.g., [3, 22]). This idea of control, which does not exploit a model of the cable flexibility, recalls a dichotomy in the field of motion planning of vibrating systems: oscillation reduction can be addressed either through model-based approaches, which exploit the dynamic model of the flexible system (see, e.g., [23–25]), or by model-free approaches that wisely reduce jerk or snap (see, e.g., [26, 27]) without considering the precise dynamic model of the oscillations.

To improve the path tracking capability without excessively increasing the control gains that would result in large oscillations (especially in the presence of flexible cables), integrators are embedded in the MPC design, leading to an MPC with embedded integrator that exploits the formulation of the dynamic model through the “difference variables”. In the literature, this kind of formulation is known as “velocity-form model” and it is an MPC formulation for offset-free tracking, as reported in [28–32]. For sake of brevity, hereinafter this kind of MPC description will be denoted as “MPC-EI” (MPC with embedded integrator).

Numerical assessment of the control performances is made through a fully-actuated, nonredundant three-DOF cable-suspended robot (i.e., with a lumped end-effector) controlled by three cables with low values of the axial stiffness. The simulated system is therefore underactuated. The effect of the actuator and sensor dynamics are included as well to obtain a reliable validation of the proposed control scheme. The paper results in a comprehensive approach for designing controllers in CDPRs that exploits the evaluation of the positive controllability, of the stability robustness through the disk margin approach, of the performance robustness through the Monte Carlo analysis, and of the computational effort of the controller steps. Another meaningful contribution of this paper is the use of a novel formulation inspired by the penalty method of multibody systems [33] to model the axial flexibility of cables in a straightforward and effective way, leading to a model representation that is easy to handle and to integrate in numerical simulations.

2 Dynamic model

2.1 Studied system

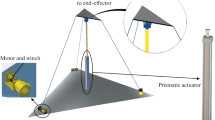
The CDPR investigated in this paper is represented in Fig. 1. It consists of an end-effector made by a lumped mass that is driven through three cables (and hence three actuators), thus resulting in a kinematically-determined, nonredundant configuration. This is a less common architecture [18] since redundant architectures are more often adopted to simplify motion planning and control (see, e.g., [34, 35]). Nonetheless, the proposed control scheme can be applied to redundant CDPRs as well. It should be noted that, in the last case, the MPC would directly perform the control distribution among the redundant control forces in an optimal manner, thus overcoming the use of suboptimal approaches to define the tensions to be exerted by each cable, such as the popular pseudoinverse approach.

Fig. 1

Scheme of the CDPR under investigation

2.2 Dynamic model of the CDPR with rigid cables

The dynamic model can be inferred by adopting the usual formalism of multibody systems, by defining the vector of the six dependent coordinates $\mathbf{q} = \left [ \begin{array}{c@{\ \ }c} \mathbf{p}^{T} & \boldsymbol{\theta}^{T} \end{array} \right ]^{T}\in \mathbb{R}^{6}$, where $\mathbf{p} = [\begin{array}{c@{\ \ }c@{\ \ }c} x & y & z]^{T} \end{array}\in \mathbb{R}^{3}$ is the vector collecting the end-effector absolute position and $\boldsymbol{\theta} = \left [ \begin{array}{c@{\ \ }c@{\ \ }c} \theta _{1} & \theta _{2} & \theta _{3} \end{array} \right ]^{T}\in \mathbb{R}^{3}$ collects the rotations of the three motors, leading to

$$ \mathbf{M} \ddot{\mathbf{q}} + \mathbf{J}^{\mathbf{T}}\boldsymbol{\lambda} = \mathbf{f}. $$

(1)

The mass matrix is defined as $\mathbf{M} = \operatorname{diag} ( m, m, m, J_{1}, J_{2}, J_{3} )\in \mathbb{R}^{6\times 6}$, where $m\in \mathbb{R}$ is the mass of the end-effector and $J_{i}\in \mathbb{R}\ ( i = 1, 2, 3)$ is the equivalent moment of inertia of each motor (that includes the contributions of the rotor, the shaft, and the drum). The external forces are collected into vector $\mathbf{f}\in \mathbb{R}^{6}$, which includes the gravity force acting in the $z$-direction, the torques exerted by the motors $\boldsymbol{\tau}_{\mathbf{m}} = \left [ \begin{array}{c@{\ \ }c@{\ \ }c} \tau _{m1} & \tau _{m2} & \tau _{m3} \end{array} \right ]^{T}\in \mathbb{R}^{3}$, and the friction forces on the motor shafts; and therefore it can be written as

$$ \mathbf{f} = \left [ \textstyle\begin{array}{c} m\mathbf{g} \\ \boldsymbol{\tau}_{\mathbf{m}} - \mathbf{F}_{\mathbf{v}}\dot{\boldsymbol{\theta}} -\boldsymbol{\tau}_{\mathbf{frict}} \end{array}\displaystyle \right ], $$

(2)

where $\mathbf{g} = [\begin{array}{c@{\ \ }c@{\ \ }c} 0 & 0 & - g]^{T} \end{array}\in \mathbb{R}^{3}$ is the vector of gravity acceleration, $\mathbf{F}_{\mathbf{v}} = \operatorname{diag} ( f_{v1}, f_{v2}, f_{v3} )\in \mathbb{R}^{3\times 3}$ is the diagonal matrix containing the motor viscous friction coefficients, while $\boldsymbol{\tau}_{\mathbf{frict}} = \left [ \begin{array}{c@{\ \ }c@{\ \ }c} \tau _{frict,1} ( t ) & \tau _{frict,2} ( t ) & \tau _{frict,3} ( t ) \end{array} \right ]^{T}\in \mathbb{R}^{3}$ is the vector whose entries are the static friction terms related to each motor. Finally, $\mathbf{J}\in \mathbb{R}^{3\times 6}$ is the Jacobian matrix of the position kinematic constraint equations, while $\boldsymbol{\lambda} \in \mathbb{R}^{3}$ collects the three Lagrange multipliers.

The kinematic constraints are obtained by assuming that cables are always taut and not slack, and hence can be treated as holonomic constraints. The fulfillment of this assumption will be enforced in the controller design by properly setting positiveness constraints on the cable tensions.

Let us consider the length of the $i$th cable, henceforth denoted as $l_{i}\in \mathbb{R}$, which is wound on a pulley whose radius is $r_{i}$ as

$$ l_{i} = l_{i0} - r_{i}\theta_{i} $$

(3)

($l_{i0}\in \mathbb{R}$ is the length of the cable when $\theta _{i} = 0$). On the other hand, $l_{i}$ can be expressed as the distance between the (fixed) $i$th exit point (denoted as $\mathbf{a}_{i}$ in Fig. 1 and whose absolute positions are collected into vector $\mathbf{a}_{i}\in \mathbb{R}^{3}$) and the end-effector position $\mathbf{p}$

$$ l_{i} = \Vert \mathbf{p} - \mathbf{a}_{i} \Vert . $$

(4)

Equation (3) and Eq. (4) lead to the $i$th constraint equation representing the $i$th cable that resembles the one of a holonomic and scleronomic constraint

$$ \sqrt{ ( l_{i0} - r_{i}\theta _{i} )^{2} - \Vert \mathbf{p} - \mathbf{a}_{i} \Vert ^{2}} = 0. $$

(5)

To meet the requirement of control theory, which usually exploits minimal ODEs (ordinary differential equations) for control design (including the design of MPC schemes), three independent ODEs can be obtained through the projection matrix $\mathbf{R}\in \mathbb{R}^{6\times 3}$,

$$ \dot{\mathbf{q}} = \mathbf{R} \dot{\mathbf{p}}. $$

(6)

The pose-dependent matrix $\mathbf{R}$ is computed as follows:

$$ \mathbf{R} = \left [ \textstyle\begin{array}{c} \mathbf{I}_{\mathbf{3}} \\ - \mathbf{P} \mathbf{V} ( \mathbf{p} )^{T} \end{array}\displaystyle \right ], $$

(7)

where $\mathbf{I}_{\mathbf{3}}\in \mathbb{R}^{3\times 3}$ is the identity matrix, $\mathbf{P} = \operatorname{diag} ( \frac{1}{r_{1}}, \frac{1}{r_{2}}, \frac{1}{r_{3}} )\in \mathbb{R}^{3\times 3}$ is the diagonal matrix containing the inverse of the radii of the three pulleys, and $\mathbf{V} ( \mathbf{p} )\in \mathbb{R}^{3\times 3}$ contains the unit vectors in the directions of the cables

$$ \mathbf{V} ( \mathbf{p} ) = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \frac{\mathbf{p} - \mathbf{a}_{1}}{l_{1}} & \frac{\mathbf{p} - \mathbf{a}_{2}}{l_{2}} & \frac{\mathbf{p} - \mathbf{a}_{3}}{l_{3}} \end{array}\displaystyle \right ]. $$

(8)

The following minimal set of three nonlinear ODEs is finally obtained to represent the overall system in the case of rigid cables:

$$ \bigl( \mathbf{R}^{\mathbf{T}}\mathbf{M} \mathbf{R} \bigr) \ddot{\mathbf{p}} + \bigl( \mathbf{R}^{\mathbf{T}}\mathbf{M} \dot{\mathbf{R}} \bigr) \dot{ \mathbf{p}} = \mathbf{R}^{\mathbf{T}}\mathbf{f}. $$

(9)

2.3 Dynamic model of the CDPR with axially-flexible cables

To account for the elastic behavior of the cables, together with their damping and inertial effects (although the latter could be neglected in the case under investigation), a formulation inspired by the penalty method used in converting DAEs to ODEs [33] is proposed in this paper. Sagging and transversal vibrations are instead neglected, as most of the papers in the literature do, by considering that the payload is much heavier compared to the cables and that proper tensioning is ensured by setting tensions lower bounds. For these reasons, several CDPRs designed under such assumptions show good performances in practice [36].

In this paper, the model of a CDPR with axially-flexible cables is developed with reference to the system under investigation, with a lumped end-effector with three DOFs. However, the proposed approach is general and can be applied to CDPRs with different architectures and with end-effector with six DOFs as well by properly formulating the governing DAEs (see, e.g., [37]). The development of this modeling approach is another novel contribution of this paper within the literature of CDPRs, as it will be explained further in this section.

Penalty-based relaxation of the constraints is usually adopted to transform a system of DAEs into a set of redundant ODEs. With reference to a generic multibody system, the Lagrange multiplier associated with the $i$th kinematic constraint $\phi _{i}$ assumes the following representation:

$$ \lambda _{i} = \alpha _{i} \bigl( \ddot{ \phi}_{i} + 2\omega _{i}\xi _{i}\dot{ \phi}_{i} + \omega _{i}^{2}\phi _{i} \bigr). $$

(10)

By means of Eq. (10), the magnitude of the generalized reaction force related to the $i$th kinematic constraint depends on the violation of the constraint $\phi _{i}$ and its first and second time-derivatives. The scalar parameters $\alpha _{i}$, $\xi _{i}$, $\omega _{i} \in \mathbb{R}$ represent the parameters of a spring-mass-damper system that is the “penalized constraint”. In this way, the “perfectly stiff” constraint (i.e., $\phi _{i} ( t ) = 0\ \forall t$) is replaced by a flexible one, whose flexibility is assumed along the direction of the constrained motion. $\alpha_{i}$, $\xi _{i}$, $\omega _{i}$ are usually treated as constant tuning parameters to be wisely chosen for trading-off between constraint violation, stability, and accuracy of the resulting ODEs. However, a proper choice of all the parameters in Eq. (10) can be exploited to provide an effective representation of the elastic properties of the system, and hence to obtain accurate estimates of the constraint reactions [38].

All these features make the penalty formulation suitable to model, in an efficient and simple way, the axial flexibility of the cables. Compared to the usual theory of the penalty formulation that assumes constant values of $\alpha _{i}$, $\xi _{i}$, $\omega _{i}$, position-dependent parameters should be adopted since the axial stiffness of each cable $k_{i}$ varies with the cable length $l_{i}$, as discussed by several papers in the literature of CDPRs (see, e.g., [35]). However, compared with the models usually adopted in the field of CDPRs, this formulation allows for the straightforward model formulation in terms of all the independent coordinates in lieu of neglecting the motor coordinates as several papers do in the field of cable robotics, also including the inertial and speed-dependent effects of cables.

By adopting a spring-mass-damper formulation for each cable, the Lagrange multipliers in Eq. (1) are reformulated in accordance with Eq. (10), leading to the following set of nonlinear ODEs:

$$ \bigl( \mathbf{M} + \mathbf{J}^{T}\mathbf{M}_{\mathbf{c}} \mathbf{J} \bigr)\ddot{\mathbf{q}} + \bigl( \mathbf{J}^{T} \mathbf{M}_{\mathbf{c}}\dot{\mathbf{J}} + \mathbf{J}^{T} \mathbf{D}_{\mathbf{c}}\mathbf{J} \bigr)\dot{\mathbf{q}} + \mathbf{J}^{T}\mathbf{K}_{\mathbf{c}}\boldsymbol{\Phi} = \mathbf{f}, $$

(11)

where $\mathbf{M}_{\mathbf{c}} ( \mathbf{q} )\in \mathbb{R}^{3\times 3}$, $\mathbf{D}_{\mathbf{c}} ( \mathbf{q} )\in \mathbb{R}^{3\times 3}$, and $\mathbf{K}_{\mathbf{c}} ( \mathbf{q} )\in \mathbb{R}^{3\times 3}$ are the (nonconstant) mass, viscous friction, and stiffness matrices. The following formulation is provided for the mass and stiffness matrices by exploiting the physical properties of the cables, i.e., Young’s modulus $E$, the cross-sectional area $S$, the linear mass density $\rho$:

$$ \mathbf{M}_{\mathbf{c}} ( \mathbf{q} ) = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \frac{1}{3}\rho l_{1} & 0 & 0 \\ 0 & \frac{1}{3}\rho l_{2} & 0 \\ 0 & 0 & \frac{1}{3}\rho l_{3} \end{array}\displaystyle \right ] ,\qquad \mathbf{K}_{\mathbf{c}} ( \mathbf{q} ) = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \frac{E S}{l_{1}} & 0 & 0 \\ 0 & \frac{E S}{l_{2}} & 0 \\ 0 & 0 & \frac{E S}{l_{3}} \end{array}\displaystyle \right ]. $$

(12)

Such a formulation of $\mathbf{M}_{\mathbf{c}} ( \mathbf{q} )$ has been obtained by imposing the equivalence of the kinetic energy of the cables that are, in practice, springs with distributed mass. The system of equations $\boldsymbol{\Phi}$ collects the three kinematic constraint equations $\phi _{i}$ ($i = 1, 2, 3$) that are not imposed to be zero because of the cable axial flexibility

$$ \phi _{i} = \sqrt{ \Vert \mathbf{p} - \mathbf{a}_{i} \Vert ^{2} - ( l_{i0} - r_{i}\theta _{i} )^{2}}. $$

(13)

As for $\mathbf{M}$, $\mathbf{J}$, $\mathbf{f}$, $\mathbf{q}$, $\dot{\mathbf{q}}$, and $\ddot{\mathbf{q}}$, they have the same meaning as the ones reported in Sect. 2.2. Since the length of the cables is pose-dependent, $\mathbf{M}_{\mathbf{c}}$ and $\mathbf{K}_{\mathbf{c}}$ are position-dependent as well and, in particular, by looking at Eq. (11), it can be noticed that the contribution of these terms is projected on the coordinates of the system through the Jacobian matrix $\mathbf{J}$. The viscous friction matrix $\mathbf{D}_{\mathbf{c}}$ has been modeled in this paper through the Rayleigh proportional damping model widely adopted in multibody systems (see, e.g., [39]), although other approaches can be exploited.

The resulting set of ODEs should be interpreted as a set of minimal ODEs since the cables are flexible along the axial directions. Consequently, the CDPR modeled in Eq. (11) is an underactuated multibody system since just three independent control forces (i.e., the three motor torques) are adopted to control the six DOFs.

3 Design of the control scheme

3.1 Control architecture: collocated vs. noncollocated control

Both the dynamic models governing the robot dynamics, either assuming rigid (Eq. (9)) and flexible (Eq. (11)) cables, are nonlinear. The direct use of Eq. (9) or Eq. (11) in the MPC design imposes the use of a nonlinear MPC scheme to cope with all the nonlinearities, thus remarkably increasing the required computational effort. Although the recent literature in the field of nonlinear MPC shows that efficient algorithms are available in the very-last years (see, e.g., [40]), the features of the dynamic model of a CDPR allow for a simpler solution, as proposed in this paper.

To allow for a simpler control design and therefore a less cumbersome computational effort of the controller equations that boosts the possibility to implement the controller in hard real-time environments, also in the presence of hardware with relatively small computational power, the control scheme proposed in this paper does not directly exploit the nonlinear model of the whole system, whose control inputs are the motor torques and whose controlled outputs are the three independent coordinates collected in $\mathbf{p}$. In contrast, a controller made by two control actions is proposed by splitting the model into two subsystems: the dynamic model relating the cable tensions and the end-effector pose, and the model relating the motor torques and the cable tensions.

Firstly, the model from the cable tensions to the motion of the suspended end-effector is considered, and feedback pose-dependent MPC with embedded integrator is formulated to compute the optimal positive tensions that ensure precise tracking of the reference spatial path. In this way, the dynamic matrix of the state-space representation of the dynamic model is constant, while just the input matrix depends on the system pose. Nonlinearities are handled by updating the model at each time step of the control loop, and then assuming the input matrix as constant along the prediction interval used for the MPC design, thus reducing the computational burden and allowing for real-time calculation. The resulting controller is therefore a nonlinear MPC, although it “locally” exploits the theory of linear MPCs. A second benefit of this formulation is that the MPC design can be done with a simple model regardless of the rigid/flexible behavior of the cable; by designing the MPC with adequate robustness, the controller will be able to tolerate both rigid and flexible cables.

Secondly, the inverse dynamic model of the motor torques, relating the motor torques and the cable tensions, is exploited to obtain the optimal reference currents for the three motors that are proportional to the commanded torques, leading to the desired tensions. This second control action is the same for both collocated control and noncollocated one, and no tension feedback is adopted.

As briefly mentioned in Sect. 1.2, two different control architectures are considered by exploiting the same control synthesis approach and formalism: a collocated control and a noncollocated control. The former is obtained when the end-effector position is evaluated, for feedback purpose, by exploiting the measurements of the winch motor encoders and the forward kinematics; therefore, in this scenario, a rigid reconstruction of the end-effector is obtained even though cables are axially-flexible. The latter, on the other hand, is obtained when the position of the end-effector is directly available through the usage of proper transducers (or state observers whose development is, however, beyond the scopes of this paper).

The representations of the two control architectures are provided in Figs. 2 and 3, which will be explained in more detail in Sect. 4.1.

Fig. 2

Architecture of the collocated control scheme, and block scheme of the simulated system

Fig. 3

Architecture of the noncollocated control scheme, and block scheme of the simulated system

3.2 Design of the MPC

3.2.1 State-space model of the end-effector

The design of the MPC-EI, in the first control action, relies on the following set of three ODEs, which represents the dynamic model of the unconstrained end-effector driven by the tensions of the three cables ($T_{i}\in \mathbb{R}$):

$$ m\ddot{\mathbf{p}} = m\mathbf{g} + \sum_{i = 1}^{3} \biggl( - T_{i}\frac{\mathbf{p} - \mathbf{a}_{i}}{ \Vert \mathbf{p} - \mathbf{a}_{i} \Vert } \biggr). $$

(14)

It should be noted that Eq. (14) holds regardless of the model assumed to represent the cables, thus allowing its use in the case of both rigid and axially-flexible cables.

By defining the state vector $\boldsymbol{\chi}_{\mathbf{c}} = \left [ \begin{array}{c@{\ \ }c} \dot{\mathbf{p}}^{T} & \mathbf{p}^{T} \end{array} \right ]^{T}\in \mathbb{R}^{6}$ and the output vector $\mathbf{y}_{\mathbf{c}}\in \mathbb{R}^{3}$, a first-order representation of Eq. (14) is inferred, leading to the following nonlinear state-space system in the continuous-time domain:

$$ \left \{ \textstyle\begin{array}{l} \dot{\boldsymbol{\chi}}_{\mathbf{c}}(t) = \mathbf{A}_{\mathbf{c}} \boldsymbol{\chi}_{\mathbf{c}}(t) + \mathbf{B}_{\mathbf{c}} ( \mathbf{p} )\mathbf{u}(t) + \mathbf{B}_{\mathbf{gc}} \mathbf{g} \\ \mathbf{y}_{\mathbf{c}}(t) = \mathbf{C}_{\mathbf{c}} \boldsymbol{\chi}_{\mathbf{c}}(t), \end{array}\displaystyle \right . $$

(15)

where the following definition of the matrices is adopted:

$$ \mathbf{A}_{\mathbf{c}} = \left [ \textstyle\begin{array}{c@{\quad}c} \mathbf{0}_{3} & \mathbf{0}_{3} \\ \mathbf{I}_{3} & \mathbf{0}_{3} \end{array}\displaystyle \right ], \qquad \mathbf{B}_{\mathbf{c}} ( \mathbf{p} ) = \left [ \textstyle\begin{array}{c} - \frac{1}{m}\mathbf{V}(\mathbf{p}) \\ \mathbf{0}_{3} \end{array}\displaystyle \right ], \qquad \mathbf{B}_{\mathbf{gc}} = \left [ \textstyle\begin{array}{c} \mathbf{I}_{3} \\ \mathbf{0}_{3} \end{array}\displaystyle \right ], \qquad \mathbf{C}_{\mathbf{c}} = \left [ \textstyle\begin{array}{c@{\quad}c} \mathbf{0}_{3} & \mathbf{I}_{3} \end{array}\displaystyle \right ]. $$

(16)

$\mathbf{A}_{\mathbf{c}}\in \mathbb{R}^{6\times 6}$ is the dynamic matrix that is constant; $\mathbf{B}_{\mathbf{gc}}\in \mathbb{R}^{6\times 3}$ is the constant input matrix of gravity acceleration that is an external input; $\mathbf{B}_{\mathbf{c}} ( \mathbf{p} )\in \mathbb{R}^{6\times 3}$ is the pose-dependent input matrix of the control tensions $\mathbf{u} = \left [ \begin{array}{c@{\ \ }c@{\ \ }c} T_{1} & T_{2} & T_{3} \end{array} \right ]^{T}\in \mathbb{R}^{3}$ (the letter $\mathbf{u}$ is used to recall a common notation used in control theory to denote the control input vector). Finally, $\mathbf{C}_{\mathbf{c}}\in \mathbb{R}^{3\times 6}$ is the output matrix and $\mathbf{0}_{3}\in \mathbb{R}^{3\times 3}$ is the null matrix.

It should be noted that the system in Eq. (15) is controllable if the usual notion of controllability of control theory is adopted by assuming unbounded control tensions, meaning that the state can be driven from any initial state to any final state in a finite time. In contrast, if controllability is evaluated with the constraint on the positive tensions, i.e., the so-called “positive controllability” is assessed, the system is not controllable. The demonstration of this property is reported in Sect. A.1, where the concept of “positive output controllability” [41] is exploited. This evaluation corroborates the challenging in motion planning and control of this system.

By discretizing the nonlinear continuous-time state-space model in Eq. (15), a set of difference equations is formulated, as required by MPC theory:

$$ \left \{ \textstyle\begin{array}{l} \boldsymbol{\chi}_{\mathbf{d}}(k + 1) = \mathbf{A}_{\mathbf{d}} \boldsymbol{\chi}_{\mathbf{d}}(k) + \mathbf{B}_{\mathbf{d}} ( \mathbf{p} ( k ))\mathbf{u}(k) + \mathbf{B}_{\mathbf{gd}} \mathbf{g} \\ \mathbf{y}_{\mathbf{d}}(k) = \mathbf{C}_{\mathbf{d}} \boldsymbol{\chi}_{\mathbf{d}}(k). \end{array}\displaystyle \right . $$

(17)

The integer scalar $k$ denotes the generic time sample; $\boldsymbol{\chi}_{\mathbf{d}}$ and $\mathbf{y}_{\mathbf{d}}$ are the discrete-time state and output vectors, respectively; $\mathbf{A}_{\mathbf{d}}\in \mathbb{R}^{6\times 6}$, $\mathbf{B}_{\mathbf{d}}\in \mathbb{R}^{6\times 3}$, $\mathbf{B}_{\mathbf{gd}}\in \mathbb{R}^{6\times 3}$, and $\mathbf{C}_{\mathbf{d}}\in \mathbb{R}^{3\times 6}$ are the discrete-time counterparts of $\mathbf{A}_{\mathbf{c}}$, $\mathbf{B}_{\mathbf{c}} ( \mathbf{p} )$, $\mathbf{B}_{\mathbf{gc}}$, and $\mathbf{C}_{\mathbf{c}}$.

Any discretization scheme, among those used in multibody system dynamics or in control theory, can be adopted to obtain the model in Eq. (17). For example, a simple yet effective discretization approach is the use of low-order exponential methods that are infrequently used in the multibody dynamics literature [42] yet widely adopted in the fields of control theory. For example, with the aim of reducing the computational effort required in the model discretization, a reasonable choice is to assume the following zero-order hold (ZOH) approximation of the control input over the time step $\Delta t$ (i.e., the sampling time of the control loop)

$$ \mathbf{u} ( t ) = \mathbf{u} ( k \Delta t ),\quad k \Delta t \le t \le ( k + 1 )\Delta t. $$

(18)

Equation (18) leads to the following form of Eq. (17):

$$ \left \{ \textstyle\begin{array}{l} \boldsymbol{\chi}_{\mathbf{d}}(k + 1) = e^{\mathbf{A}_{\mathbf{c}}\Delta t} \boldsymbol{\chi}_{\mathbf{d}}(k) + ( \int _{0}^{\Delta t} e^{\mathbf{A}_{\mathbf{c}}\tau} \mathbf{B}_{\mathbf{c}} ( \mathbf{p} ( k ) )d\tau )\mathbf{u}(k) + ( \int _{0}^{\Delta t} e^{\mathbf{A}_{\mathbf{c}}\tau} d\tau )\mathbf{B}_{\mathbf{gc}}\mathbf{g} \\ \mathbf{y}_{\mathbf{d}}(k) = \mathbf{C}_{\mathbf{d}} \boldsymbol{\chi}_{\mathbf{d}}(k). \end{array}\displaystyle \right . $$

(19)

Comparing Eq. (19) and Eq. (17) clearly reveals the expressions of the matrices of the discrete-time state-space

$$ \begin{aligned} \mathbf{A}_{\mathbf{d}} &= e^{\mathbf{A}_{\mathbf{c}}\Delta t}, \qquad \mathbf{B}_{\mathbf{d}} \bigl( \mathbf{p} ( k ) \bigr) = \int _{0}^{\Delta t} e^{\mathbf{A}_{\mathbf{c}}\tau} \mathbf{B}_{\mathbf{c}} \bigl( \mathbf{p} ( k ) \bigr) d\tau ,\\ \mathbf{B}_{\mathbf{gd}} &= \biggl( \int _{0}^{\Delta t} e^{\mathbf{A}_{\mathbf{c}}\tau} d\tau \biggr) \mathbf{B}_{\mathbf{gc}}, \qquad \mathbf{C}_{\mathbf{d}} = \mathbf{C}_{\mathbf{c}} . \end{aligned} $$

(20)

By assuming $\mathbf{B}_{\mathbf{c}} ( \mathbf{p} ( k ) )$ as constant over $\Delta t$, which is consistent with using a ZOH, the following discrete-time input matrix is obtained:

$$ \mathbf{B}_{\mathbf{d}} \bigl( \mathbf{p} ( k ) \bigr) = \mathbf{A}_{\mathbf{c}}^{ - 1} \bigl( e^{\mathbf{A}_{\mathbf{c}}\Delta t} - \mathbf{I} \bigr)\mathbf{B}_{\mathbf{c}} \bigl( \mathbf{p} ( k ) \bigr). $$

(21)

Since the exact evaluation of matrix exponentials can be very demanding from the computational point of view, $\mathbf{A}_{\mathbf{d}}$ and $\mathbf{B}_{\mathbf{d}}$ can be further approximated through low-order Padè approximants or Taylor’s series expansions [43]. For example, in this work, a first-order approximation, which can be seen as both the first-order Taylor’s series expansions and the ($1,0$) Padé approximants, is adopted:

$$ e^{\mathbf{A}_{\mathbf{c}}\Delta t} \approx \mathbf{I} + \mathbf{A}_{\mathbf{c}}\Delta t, $$

(22)

which, finally, leads to the following matrices of the discrete-time state-space in Eq. (17):

$$ \mathbf{A}_{\mathbf{d}} = \mathbf{I} + \Delta t \mathbf{A}_{\mathbf{c}}, \qquad\mathbf{B}_{\mathbf{d}} \bigl( \mathbf{p} ( k ) \bigr) = \Delta t \mathbf{B}_{\mathbf{c}} \bigl( \mathbf{p} ( k ) \bigr), \qquad \mathbf{B}_{\mathbf{gd}} = \Delta t \mathbf{B}_{\mathbf{gc}}, \qquad \mathbf{C}_{\mathbf{d}} = \mathbf{C}_{\mathbf{c}}. $$

(23)

This choice remarkably reduces the computational effort without introducing noticeable discretization errors in the controller design. Higher-order discretization methods, as well as higher-order approximations of the exponential, could be used at the cost of an increase of the computational effort.

3.2.2 Embedding of the integrator

To embed the integrator within the MPC design with the goal of ensuring precise path tracking, the so-called “difference variables” are introduced

$$ \boldsymbol{\Delta} \boldsymbol{\chi}_{\mathbf{d}}(k) = \boldsymbol{ \chi}_{\mathbf{d}}(k) - \boldsymbol{\chi}_{\mathbf{d}}(k - 1), $$

(24)

$$ \boldsymbol{\Delta} \mathbf{u}(k) = \mathbf{u}(k) - \mathbf{u}(k - 1). $$

(25)

Therefore, the augmented state vector $\boldsymbol{\chi} \in \mathbb{R}^{9}$ is adopted

$$ \boldsymbol{\chi} (k) = \left [ \textstyle\begin{array}{c} \boldsymbol{\Delta} \boldsymbol{\chi}_{\mathbf{d}}(k) \\ \mathbf{y}_{\mathbf{d}}(k) \end{array}\displaystyle \right ]. $$

(26)

Finally, the following augmented first-order model is formulated:

$$ \left \{ \textstyle\begin{array}{l} \boldsymbol{\chi} (k + 1) = \mathbf{A} \boldsymbol{\chi} (k) + \mathbf{B} ( \mathbf{p} ( k ) ) \boldsymbol{\Delta} \mathbf{u}(k) \\ \mathbf{y}(k) = \mathbf{C} \boldsymbol{\chi} (k), \end{array}\displaystyle \right . $$

(27)

where $\mathbf{A}\in \mathbb{R}^{9\times 9}$, $\mathbf{B} ( \mathbf{p} ( k ) )\in \mathbb{R}^{9\times 3}$, $\mathbf{C}\in \mathbb{R}^{3\times 9}$ are defined as

$$ \mathbf{A} = \left [ \textstyle\begin{array}{c@{\quad}c} \mathbf{A}_{\mathbf{d}} & \mathbf{0}_{6 \times 3} \\ \mathbf{C}_{\mathbf{d}}\mathbf{A}_{\mathbf{d}} & \mathbf{I}_{3} \end{array}\displaystyle \right ], \qquad\mathbf{B} \bigl( \mathbf{p} ( k ) \bigr) = \left [ \textstyle\begin{array}{c} \mathbf{B}_{\mathbf{d}} ( \mathbf{p} ( k ) ) \\ \mathbf{C}_{\mathbf{d}}\mathbf{B}_{\mathbf{d}} ( \mathbf{p} ( k ) ) \end{array}\displaystyle \right ], \qquad \mathbf{C} = \left [ \textstyle\begin{array}{c@{\quad}c} \mathbf{0}_{3 \times 6} & \mathbf{I}_{3} \end{array}\displaystyle \right ]. $$

(28)

Again, as in the continuous-time model, $\mathbf{A}$ and $\mathbf{C}$ are constant matrices, while $\mathbf{B} ( \mathbf{p} ( k ))$ changes with the pose.

3.2.3 Evaluation of the prediction matrices for MPC with embedded integrator

The computation of the optimal tensions by the MPC-EI is based on the prediction of the state trajectory over the prediction horizon $N_{p}\in \mathbb{N}^{+}$. Due to the presence of a variable input matrix $\mathbf{B} ( \mathbf{p} ( k ) )$, the dynamic model adopted for prediction is updated at each time step $k$ based on the pose. In the case of collocated control architecture, the pose is the one estimated through the forward kinematic model; in the case of noncollocated, it is the measured one. Then, such a model is kept constant over the whole prediction horizon to predict the state (and the output) with a smaller computational effort. Hence, the output vector predicted at each time step, denoted as $\mathbf{Y}\in \mathbb{R}^{3 N_{p}}$ (by assuming a vectorial representation of the prediction over the whole prediction horizon), is described through the following linear model:

$$ \mathbf{Y} = \mathbf{Fx}(k_{i}) + \boldsymbol{\Theta} \bigl( \mathbf{p} ( k_{i} ) \bigr)\boldsymbol{\Delta} \mathbf{u}_{\mathbf{N}_{\mathbf{c}}}, $$

(29)

where $\mathbf{F}\in \mathbb{R}^{3 N_{p} \times 9}$ and $\boldsymbol{\Theta} ( \mathbf{p} ( k_{i} ) )\in \mathbb{R}^{3 N_{p} \times 3 N_{c}}$ are defined as

$$ \begin{aligned} \mathbf{F} &= \left [ \textstyle\begin{array}{c} \mathbf{CA} \\ \mathbf{CA}^{2} \\ \vdots \\ \mathbf{CA}^{N_{p}} \end{array}\displaystyle \right ], \\ \boldsymbol{\Theta} \bigl( \mathbf{p} ( k_{i} ) \bigr) &= \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \mathbf{CB} ( \mathbf{p} ( k_{i} ) ) & \mathbf{0} & \cdots & \mathbf{0} \\ \mathbf{CAB} ( \mathbf{p} ( k_{i} ) ) & \mathbf{CB} ( \mathbf{p} ( k_{i} ) ) & \cdots & \mathbf{0} \\ \vdots & \vdots & \vdots & \vdots \\ \mathbf{CA}^{N_{p} - 1}\mathbf{B} ( \mathbf{p} ( k_{i} ) ) & \mathbf{CA}^{N_{p} - 2}\mathbf{B} ( \mathbf{p} ( k_{i} ) ) & \cdots & \mathbf{CA}^{N_{p} - N_{c}}\mathbf{B} ( \mathbf{p} ( k_{i} ) ) \end{array}\displaystyle \right ]. \end{aligned} $$

(30)

The tuning parameter $N_{c}\in \mathbb{N}^{+}$ is the control horizon, and it indicates the number of samples along which the optimal control action will be spread.

3.2.4 Constrained optimization problem: formulation and solution

The path tracking problem is translated into the MPC design by defining a suitable objective function to minimize, $\Psi \in \mathbb{R}$, trading between the requirements of reducing the error and the control effort. In this paper, to ensure adequate smoothness that allows handling the presence of cable flexibility, the control effort is included in $\Psi$ through the tension time-derivatives, which is in turn represented through the tension variation $\boldsymbol{\Delta} \mathbf{u}$ defined in Eq. (25). The following cost function is therefore adopted:

$$ \Psi = \bigl(\mathbf{Y}^{\mathbf{ref}} - \mathbf{Y}\bigr)^{T} \mathbf{R}_{\mathbf{Y}}\bigl(\mathbf{Y}^{\mathbf{ref}} - \mathbf{Y}\bigr) + \boldsymbol{\Delta} \mathbf{u}_{\mathbf{N}_{\mathbf{c}}}^{T} \mathbf{R}_{\boldsymbol{\Delta} \mathbf{u}}\boldsymbol{\Delta} \mathbf{u}_{\mathbf{N}_{\mathbf{c}}}. $$

(31)

In Eq. (31), $\mathbf{R}_{\mathbf{Y}}\in \mathbb{R}^{3 N_{p} \times 3 N_{p}}$ and $\mathbf{R}_{\boldsymbol{\Delta} \mathbf{u}}\in \mathbb{R}^{3 N_{c} \times 3 N_{c}}$ are weighing matrices adopted to tune the controller; $\mathbf{Y}^{\mathbf{ref}}\in \mathbb{R}^{3 N_{p}}$ is the vector of the predicted desired trajectories over the prediction horizon, represented through the vector of reference trajectories (defined at the time step $k_{i}$)

$$ \mathbf{Y}^{\mathbf{ref}} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \mathbf{I}_{3} & \mathbf{I}_{3} & \cdots & \mathbf{I}_{3} \end{array}\displaystyle \right ]^{T} \mathbf{r}(k_{i}) = \mathbf{F}^{\mathbf{ref}}\mathbf{r}(k_{i}) $$

(32)

($\mathbf{F}^{\mathbf{ref}}\in \mathbb{R}^{3 N_{p} \times 3}$ is introduced for brevity of representation). Vector $\boldsymbol{\Delta} \mathbf{u}_{\mathbf{N}_{\mathbf{c}}}\in \mathbb{R}^{3 N_{c}}$ collects the optimal values of tension variations for the three cables over the control horizon lasting $N_{c}$ samples.

Bounds on the feasible tensions of the three cables $\mathbf{u}(k)$ are accounted for in the control design by means of upper ($\mathbf{u}_{\mathbf{max}} = T_{\max} \left [ \begin{array}{c@{\ \ }c@{\ \ }c} 1 & 1 & 1 \end{array} \right ]^{T}\in \mathbb{R}^{3}$) and lower ($\mathbf{u}_{\mathbf{min}} = T_{\min} \left [ \begin{array}{c@{\ \ }c@{\ \ }c} 1 & 1 & 1 \end{array} \right ]^{T}\in \mathbb{R}^{3}$) bounds. $T_{\min} \in \mathbb{R}^{+}$ sets the positiveness tension requirements, together with a certain safety margin; $T_{\max} \in \mathbb{R}^{+}$ embeds the constraint on the maximum admissible strain to avoid cable failure. Since MPC-EI formulates the cost function in terms of $\boldsymbol{\Delta} \mathbf{u}$, constraints on the tension variations can be easily included as well, to ensure bounded derivatives of tensions and hence improve smoothness of the control action by avoiding jerky motion: $\Delta T_{\min} \in \mathbb{R}$ and $\Delta T_{\max} \in \mathbb{R}$ are introduced to represent the minimum and the maximum admissible cable tension variations, respectively, leading to $\boldsymbol{\Delta} \mathbf{u}_{\mathbf{min}} = \Delta T_{\min} \left [ \begin{array}{c@{\ \ }c@{\ \ }c} 1 & 1 & 1 \end{array} \right ]^{T}\in \mathbb{R}^{3}$ and $\boldsymbol{\Delta} \mathbf{u}_{\mathbf{max}} = \Delta T_{\max} \left [ \begin{array}{c@{\ \ }c@{\ \ }c} 1 & 1 & 1 \end{array} \right ]^{T}\in \mathbb{R}^{3}$. Details on the inclusion of the boundaries are provided in Sect. A.2 and A.3.

The solution of the control design problem relies on quadratic programming algorithms in the presence of linear inequalities. For example, in this work Hildreth’s method [44] is adopted, which ensures fast computation and good numerical conditioning, and hence it is suitable for real-time computation.

The solution of the optimization problem defined through the cost function in Eq. (31) leads to the vector of the optimal predicted control inputs over the control horizon $N_{c}$, which is expressed in the following vectorial form:

$$ \boldsymbol{\Delta} \mathbf{u}_{\mathbf{N}_{\mathbf{c}}} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \boldsymbol{\Delta} \mathbf{u}^{T}(k_{i}) & \boldsymbol{\Delta} \mathbf{u}^{T}(k_{i} + 1) & \cdots & \boldsymbol{\Delta} \mathbf{u}^{T}(k_{i} + N_{c} - 1) \end{array}\displaystyle \right ]^{T}. $$

(33)

This predicted optimal control action, however, is not going to be applied directly one by one in a consecutive manner, otherwise an open-loop controller would be achieved. Indeed, to avoid this aspect, in accordance with the receding horizon principle, only the control action related to the first sample, in this particular case the three entries of $\boldsymbol{\Delta} \mathbf{u}(k_{i})$, is considered and then transformed into the commanded tensions to be exerted, while the other ones are discarded. This process is repeated at each time step.

3.3 Computation of the motor torques

The optimal values of the cable tensions computed by the MPC-EI, here denoted by $T_{i}^{MPC}$ (that are collected into vector $\mathbf{u}^{MPC}$), are fed into the second term of the controller to transform them into the commanded torques (and hence currents) for the three motors. This transformation relies on the dynamic model of each motor that is represented through the following ODE:

$$ J_{i}\ddot{\theta}_{i} ( t ) + f_{v,i}\dot{ \theta}_{i} ( t ) + \tau _{frict,i} ( t ) = \tau _{m,i} ( t ) - T_{i} ( t ) r_{i}. $$

(34)

In particular, $\theta _{i}\in \mathbb{R}$ is the absolute rotation of the shaft of the $i$th motor; $J_{i}\in \mathbb{R}$ is the moment of inertia of the rotor, plus the drum and idle pulleys; $f_{v,i}\in \mathbb{R}$ is the viscous friction coefficient; $\tau _{frict,i}\in \mathbb{R}$ is the static friction; $\tau _{m,i}\in \mathbb{R}$ is the motor torque; $r_{i}\in\mathbb{R}$ is the radius of the drum.

Since no feedback of the actual tensions is supposed to be available, a model-based approach is exploited to compute the motor torques $\tau _{m,i}$ that lead to the required cable tensions. Let us compute the reference acceleration $\ddot{\theta}_{i}^{ref}(t)$ and speed $\dot{\theta}_{i}^{ref}(t)$ by means of the inverse kinematics, which is expressed in vectorial form as follows, where $\dot{\boldsymbol{\theta}}^{\mathbf{ref}}$, $\ddot{\boldsymbol{\theta}}^{\mathbf{ref}}$ and $\dot{\mathbf{p}}^{\mathbf{ref}}$, $\ddot{\mathbf{p}}^{\mathbf{ref}}$ denote the speed and acceleration references:

$$ \dot{\boldsymbol{\theta}}^{\mathbf{ref}} = \bigl[ - \mathbf{P} \mathbf{V} ( \hat{\mathbf{p}} )^{T} \bigr]\dot{\mathbf{p}}^{\mathbf{ref}}, $$

(35)

$$ \ddot{\boldsymbol{\theta}}^{\mathbf{ref}} = \bigl[ - \mathbf{P} \mathbf{V} ( \hat{\mathbf{p}} )^{T} \bigr]\ddot{\mathbf{p}}^{\mathbf{ref}} - \bigl[ \mathbf{P} \dot{\mathbf{V}} ( \hat{\mathbf{p}} )^{T} \bigr] \dot{\mathbf{p}}^{\mathbf{ref}}. $$

(36)

$\hat{\mathbf{p}}$ is the estimated value of $\mathbf{p}$ in the case of collocated control by means of the forward kinematics with the measured $\boldsymbol{\theta}$; in contrast, it is the measured pose in the case of noncollocated control.

Hence, the algebraic inverse dynamic model is exploited as follows for each motor:

$$ \tau _{m,i} = J_{i}\ddot{\theta}_{i}^{ref}(t) + f_{v,i}\dot{\theta}_{i}^{ref}(t) + \tau _{frict,i} ( t ) + r_{i}T_{i}^{MPC}(t). $$

(37)

The required motor torques are, in turn, transformed into the commanded currents for the three independent motor current controllers $i_{i}^{ref}$ by taking advantage of the motor torque constant $k_{t,i}$:

$$ i_{i}^{ref} = \frac{\tau _{m,i}}{k_{t,i}}. $$

(38)

4 Numerical results

4.1 System description

Both rigid and flexible cables have been considered in the controller application to evaluate the performances of the closed-loop system under both assumptions. A CSPR with perfectly stiff cables has been simulated through Eq. (9), while the robot with axially-flexible cables has been simulated through Eq. (11). To propose a severe test for the proposed controller, very flexible cables are assumed with $ES = 24.9~\text{kN}$. This value was taken from [12] as a meaningful example of a flexible CDPR since it uses values of $ES$ that are smaller of several order of magnitudes if compared to other papers (see, e.g., [35]). Clearly, just one control architecture is implemented in the case of rigid cables.

All the simulators have been implemented in the Matlab/Simulink environment by also including a simplified dynamic model of the servo-controlled electric motors, whose frequency response is modeled as a first order linear system with bandwidth equal to $2~\text{kHz}$, as typically occurs in off-the-shelf brushless motors (see, e.g., [45]). Focusing the attention on the collocated control architecture, the three motors are supposed to be equipped with encoders characterized by 14,400 pulses per revolution (that are standard values for commercial encoders). Speed estimation is made by means of numerical derivatives plus low pass filtering. The presence of quantization noise and phase lag, due to low pass filtering, creates a realistic test case that prevents excessive increases of the controller gains. No other sensors are available; the controller therefore relies on just the motor encoder measurements. In the case of collocated control architecture, the following position forward kinematics equations are adopted by taking advantage of the dimensions sketched in Fig. 1 (with the following Cartesian coordinates of the cable exit points: $\mathbf{a}_{1} = \left [ \begin{array}{c@{\ \ }c@{\ \ }c} - \frac{l}{2} & \frac{w}{2} & 0 \end{array} \right ]^{T}$, $\mathbf{a}_{2} = \left [ \begin{array}{c@{\ \ }c@{\ \ }c} \frac{l}{2} & \frac{w}{2} & 0 \end{array} \right ]^{T}$, $\mathbf{a}_{3} = \left [ \begin{array}{c@{\ \ }c@{\ \ }c} 0 & - \frac{w}{2} & 0 \end{array} \right ]^{T}$):

$$ \begin{aligned} x &= \frac{l_{1}^{2} - l_{2}^{2}}{2l}, \\ y &= \frac{ - 2l_{1}^{2} - 2l_{2}^{2} + 4l_{3}^{2} + l^{2}}{8w}, \\ z &= - \sqrt{l_{3}^{2} - x^{2} - \biggl( y + \frac{w}{2} \biggr)^{2}}. \end{aligned} $$

(39)

As for the speed forward kinematics problem, the relationship between $\dot{\mathbf{p}}$ and $\dot{\boldsymbol{\theta}}$ can be easily inferred from proper partitioning of matrix $\mathbf{R}$ in Eq. (6).

Focusing now the attention on the noncollocated control architecture, the end-effector is supposed to be sensed by proper sensors (e.g., cameras), supported by an acquisition board with 12 bits. This coarse number of bits has been intentionally chosen to reproduce a severe scenario with relevant measurement noise, introduced by the quantization, that imposes filtering the numerical derivatives adopted in the speed estimation (and hence reproducing a more realistic scenario where speed estimation is affected by lag).

To better understand the differences between the two control architectures, Figs. 2 and 3 provide their block schemes. The collocated scheme is shown in Fig. 2: the position of the end-effector is estimated through the motor encoder measurements and the forward kinematics ($\hat{\mathbf{p}}$ denotes the estimated position); filtered numerical derivatives are employed to estimate the end-effector speeds ($\hat{\dot{\mathbf{p}}}$ denotes the estimated speed). The noncollocated scheme is shown in Fig. 3: the end-effector position is directly available ($\hat{\mathbf{p}}$ should be therefore treated as the measured value of $\mathbf{p}$ that includes noise as well), while numerical derivatives are again exploited to get the velocity vector. In both schemes, $\hat{\mathbf{p}}$ and $\hat{\dot{\mathbf{p}}}$ are exploited within the MPC algorithm (formulated through the embedding of the integrator), and the same inverse dynamics model of the motors is adopted.

In the control implementation, the sample time $\Delta t$ is chosen to be $2 \times 10^{ - 3}~\text{s}$ as a trade-off between the need of granting adequate controller bandwidth and reducing the number of calculations required to solve the optimal control problem. The tuning parameters of the controller and the physical parameters of the simulated robot are listed in Table 1.

Table 1 System parameters

Three different reference paths are tested and proposed in the following sections to highlight different features of the proposed control scheme and its effectiveness in tracking spatial paths with reduced contour errors and negligible excitations of the cable flexibility. The same tuning of the controller parameters is adopted for all the test cases, both in the presence of rigid and elastic cables and both with collocated and noncollocated control, to show the capability of the designed MPC to handle different cable behaviors and feedback variables. Comparison with a MPC without embedding the integrator is also provided in one of the tests to show the benefit of the chosen formulation.

4.2 Test cases

4.2.1 Test 1: point-to-point motion with an unfeasible trajectory

The first trajectory consists of a descending step reference along the $z$-axis, while keeping the references on $x$-axis and $y$-axis unchanged. This trajectory is unfeasible since tracking the discontinuous commanded position imposes negative infinite speeds and accelerations along the $z$-axis, thus causing negative tensions, and hence leading to a possible slack condition for the cables. For this reason, it is never used for motion planning in CDPRs (and, in general, in underactuated multibody systems as well).

The temporal tracking responses of both collocated control and noncollocated one are reported in Fig. 4, which reveals that both closed-loop systems are able to ensure a quick and accurate settling to the final target position with just a small overshoot, even in the presence of highly flexible cables. Such a response is achieved thanks to the formulation with embedded integrator and to the presence of penalization and hard constraints on the tension derivatives.

Fig. 4

Temporal tracking responses with step reference: rigid model (a), flexible cables with collocated control (b), flexible cables with noncollocated control (c)

In the case of rigid cables, the controller ensures no steady-state error since the estimation of the position obtained through forward kinematics is exact (except for the error due to the encoder quantization). The same result is achieved with the noncollocated controller and the flexible cables, since it allows to compensate the static deflection, ensuring a zero error at steady-state conditions. In contrast, in the case of flexible cables with a collocated controller, both initial and final positions do not match the target one because of the static cable elongation. It should be noted that such an error cannot be compensated by this control architecture because it does not sense it.

The cable tensions are shown in Fig. 5, which clearly confirms the capability of the proposed control scheme to ensure bounded and smooth tensions. In the case of flexible cables, the actual tensions go slightly beyond the lower bound of $10~\text{N}$ in both collocated and noncollocated control schemes by reaching the minimum value of $6.8~\text{N}$, which is, however, not critical if just a small safety margin is chosen in setting the lower bounds. Figure 5.c shows a slightly noisy behavior of tensions in the case of noncollocated control. Such small oscillations are caused by the rough position sensor that is assumed to be quantized through a 12-bit acquisition board.

Fig. 5

Cable tensions with step reference: rigid model (a), flexible cables with collocated control (b), flexible cables with noncollocated control (c)

4.2.2 Performance robustness against model parameter mismatches

Performance robustness against parameter uncertainty is investigated by assessing the tracking performances in the presence of model mismatches. A first assessment has been carried out by considering the relevant $\pm40\%$ mismatches on each parameter, while assuming the nominal values for the other ones, to evaluate the impact of each perturbation on the control performances. The results sported by the noncollocated control scheme is here discussed since this control architecture is usually the least robust one [46]. The results are summarized in Fig. 6 where the RMS (root mean square) values of the tracking error (in the interval from 0 to 3 s) are reported with the reference to Test 1 (i.e., the step response) and with the flexible cables. This test has been chosen for performance robustness evaluation since it is the most challenging one due to three main reasons: first, the tension lower bound is reached by all the cable tensions; secondly, it is an unfeasible trajectory since it is discontinuous at the position level; finally, it imposes the highest accelerations and a higher harmonic content, therefore leading to the greatest excitation of the axially-flexible cables. As it can be seen from Fig. 6, the perturbations that mostly affect the trajectory tracking response are those related to the radius of the pulleys and to the mass of the end-effector, although the highest increment is just $+ 6 \%$ compared to the nominal case (denoted in Fig. 6 as “nom”).

Fig. 6

Contribution of each model parameter perturbation in terms of RMS error with Test 1

A second assessment has been performed by performing a Monte Carlo analysis, where 100 simulations have been performed with random perturbations of all the parameters simultaneously. Gaussian distributions have been assumed, characterized by a mean value equal to the nominal one and by a standard deviation equal to $40\%$ of the mean. The results of this second assessment are summarized through the time histories of the end-effector motion in the vertical axis reported in Fig. 7, which shows the uncertainty band arising from such perturbations. The average RMS error (in the interval from 0 to 3 s) is $0.211~\text{m}$, i.e., $+ 1\%$ compared to the nominal case.

Fig. 7

System responses in the Monte Carlo analysis

All these results have shown that performances are adequately robust with respect to this kind of significant uncertainties. Additionally, the stability of the closed loop system has been obtained for all the perturbed tests.

4.2.3 Discussion on the computational effort

This section discusses the issue regarding the computational effort by analyzing the required CPU time at each time step to evaluate whether the proposed controller architectures are suitable to be performed in real-time controllers. The case of the collocated controller is shown since is the most demanding one due to the presence of the forward kinematics. The numerical results have been obtained using a laptop PC with a $16.0~\text{GB}$ RAM and an octa-core processor (11th Gen Intel^(R) Core ^(TM) i7-11800H) characterized by a clock frequency of $2.30~\text{GHz}$. It should be noted that no parallel computing has been adopted, and therefore just one core performs calculation.

The entire control algorithm can be described as a sequence of the following actions: update of continuous input matrix $\mathbf{B}_{\mathbf{c}} ( \mathbf{p} )$ through Eq. (16) (including the estimation of the pose through the forward kinematics in Eq. (39)); discretization of the continuous state-space model through Eq. (23); condensing process for the evaluation of the prediction matrices $\mathbf{F}$ and $\boldsymbol{\Theta} ( \mathbf{p} ( k_{i} ) )$ through Eq. (30); constrained minimization of the cost function $\Psi$ expressed in Eq. (31); evaluation of the commanded motor torques $\tau _{m,i}$ for each motor by exploiting Eq. (37). Figure 8 summarizes the CPU time required at each time step with reference to Test 1 by highlighting the contributions of all the operations. Such a test has been chosen to be shown since it is the most critical one for the minimization of the cost function of the MPC-EI algorithm due to the achievement of the tension lower bounds in part of the motion. Slightly smaller computational efforts are required in the other tests, and therefore they are omitted for brevity.

Fig. 8

CPU times required for each process that constitutes the proposed control algorithm, with both collocated and noncollocated architecture, during step response

More precisely, Fig. 8 shows the elapsed times of the different steps characterizing the “MPC-EI” block reported in Fig. 2 together with the elapsed time required by the “Motor inverse dynamics” block. The “Inverse kinematics” block does not contribute to the computational effort in real-time scenarios since its evaluation is performed offline; however, its inclusion, in the real-time calculation at each step would not be critical since the average value of its offline computational time is equal to just $1.1 \times 10^{ - 5}~\text{s}$ for each time step. In contrast, the “Forward kinematics” block is computed online (although its contribution is almost negligible since the average computational time is equal to $1.7 \times 10^{ - 6}~\text{s}$). Comparing the overall CPU time at each time step with the control sampling time $\Delta t = 2 \times 10^{ - 3}~\text{s}$ clearly highlights that the proposed controller is not so demanding, requiring a maximum value equal to $7.9 \times 10^{ - 4}~\text{s}$ and an average equal to $4.9 \times 10^{ - 4}~\text{s}$. It should be noted that the computational effort could be further decreased by optimizing the code implementing the control scheme. This issue will be objective of further investigations.

4.2.4 Test 2: triangular path

The proposed control schemes

The second test case consists of a planar triangular path (in a horizontal plane placed at $z = - 0.5~\text{m}$), where each side is performed in a motion time of $2~\text{s}$ through a 5th-degree polynomial, rest-to-rest motion law. A rest interval of $1~\text{s}$ is included at each vertex of the planar triangle, leading to an overall execution time of $10~\text{s}$. The path tracking response is shown in Fig. 9: the executed paths are almost overlapped with the reference path (denoted in the figures as “Ref”), in the presence of both rigid and elastic cables.

Fig. 9

Path tracking responses with triangular reference: rigid model (a), flexible cables with collocated control (b), flexible cables with noncollocated control (c)

A deeper evaluation of the results can be inferred from Fig. 10, which shows the contour errors that are defined as the difference between the reference and the actual path. For each controller, two different evaluations are done: the planar contour error, computed just along the $x$ and $y$ directions by neglecting the positioning of the triangle in the vertical direction, and the spatial contour error that considers the three dimensions. In the case of rigid cables, the two errors are almost overlapped: the maximum value is $3.8~\text{mm}$ and the RMS value is $1.3~\text{mm}$ if the planar case is considered, while the maximum value and the RMS one are $3.9~\text{mm}$ and $1.3~\text{mm}$, respectively, if the spatial case is taken into account. In the presence of flexible cables with the collocated control architecture, its maximum and RMS values are, respectively, $4.0~\text{mm}$ and $1.5~\text{mm}$ for the planar contour error and $9.9~\text{mm}$ and $8.1~\text{mm}$ for the spatial one. The presence of a small planar error is related to the capability of the MPC to track the desired path without relevant oscillations thanks to the smooth control action computed by the designed controller. However, both the errors are affected by the static cable deformations that are exacerbated along the $z$ direction. As already mentioned, such a static error cannot be detected by the encoders nor controlled by the collocated control architecture. Finally, if the noncollocated control is considered, the two contour errors are almost overlapped and approach those obtained in the case of rigid cables. Indeed, such an architecture is able to detect and to compensate for the static cable deformations, leading to maximum and RMS values that are, respectively, $3.9~\text{mm}$ and $1.3~\text{mm}$ when the planar evaluation is carried out, while the maximum value is $4.1~\text{mm}$ and the RMS is $1.3~\text{mm}$ if the spatial contour error is considered.

Fig. 10

Contour errors with triangular reference: rigid model (a), flexible cables with collocated control (b), flexible cables with noncollocated control (c)

Finally, the cable tensions are shown in Fig. 11, which confirms that bounds are satisfied and smooth tension changes are obtained as required in the controller design: despite the cable flexibility, no meaningful oscillations appear at the frequency components of motion. Just some small amplitude, high frequency oscillations are excited by the quantization errors of the encoders that lead to noisy sensed position and estimated speed. Control gains could be reduced if the feedback controller would be supported by a feedforward compensation of the load gravity and inertia forces, as is often done in controlling CDPRs; however, in this work it is not accounted for to provide a more severe test for the proposed feedback controller.

Fig. 11

Cable tensions with triangular reference: rigid model (a), flexible cables with collocated control (b), flexible cables with noncollocated control (c)

Use of a benchmark controller

To further stress the benefits of the proposed control scheme, a “classical” MPC formulation without embedded integrator is also implemented. With the goal to make this comparison as fair as possible, the same prediction and control horizon are assumed. In contrast, the weight $\mathbf{R}_{\mathbf{u}}$ (which is used instead of the previously mentioned $\mathbf{R}_{\boldsymbol{\Delta} \mathbf{u}}$ since in this case the state-space model is not described through difference variables) has been tuned again to look for the “best tuning” by showing the results of two different choices of such a matrix. A first controller has been designed by setting $\mathbf{R}_{\mathbf{u}} = 5 \times 10^{ - 6} \mathbf{I}_{3}$, which will be denoted as the “expensive controller” since it is aimed at obtaining more precise path tracking at the cost of large control effort, i.e., large tensions; secondly, a smoother tuning has been obtained by setting $\mathbf{R}_{\mathbf{u}} = 5 \times 10^{ - 5} \mathbf{I}_{3}$, which will be indicated as the “cheap controller”, to increase the penalty of large control efforts. Figure 12 shows the path tracking results for both the benchmark controllers. It is evident that higher gains allow to achieve an acceptable path tracking response when the rigid model is taken into account; this result degrades significantly if axially-flexible cables are considered. In contrast, the MPC controller with $\mathbf{R}_{\mathbf{u}} = 5 \times 10^{ - 5} \mathbf{I}_{3}$ leads to large errors also in the presence of the rigid model and this result tends to get worse and worse as long as axial flexibility of the cables is considered. The evaluation of the contour errors, shown in Fig. 13, reveals that larger errors are obtained by both controllers, with both collocated and noncollocated controller, compared with those provided by the MPC-EI. The “expensive controller” leads to a maximum contour error equal to $13.8~\text{mm}$ and to an RMS value of $4.9~\text{mm}$ when the rigid model response is considered; these values remarkably increase if the flexible model is controlled through the collocated scheme, reporting a maximum contour error of $63.4~\text{mm}$ and an RMS value equal to $24.6~\text{mm}$, and they get even worse through the noncollocated one, showing a maximum value and an RMS one equal to $131.7~\text{mm}$ and $42.6~\text{mm}$, respectively. In contrast, the “cheap controller” has a maximum contour error equal to $18.6~\text{mm}$ with an RMS value of $6.3~\text{mm}$ if the rigid model response is taken into account; these values remarkably degrade if the flexible model response, in the presence of the collocated control scheme, is considered, leading to a maximum contour error of $85.1~\text{mm}$ and an RMS value equal to $32.1~\text{mm}$. Their values get even worse in the presence of the noncollocated controller, showing a maximum value equal to $143.1~\text{mm}$ and an RMS value of $58.0~\text{mm}$. In both cases, low frequency oscillations appear due to the controller and the cable flexibility.

Fig. 12

Path tracking responses with triangular reference: benchmark controllers with different tuning parameters in the presence of rigid model (a, d), flexible cables with collocated control (b, e), flexible cables with noncollocated control (c, f)

Fig. 13

Contour errors with triangular reference: benchmark controllers with different tuning parameters in the presence of rigid model (a, d), flexible cables with collocated control (b, e), flexible cables with noncollocated control (c, f)

4.2.5 Test 3: spiral path

The last test case considers a more complex scenario: an ascending spatial Archimedean spiral path. To define such a path, polar coordinates ($r$, $\beta$) are assumed in the $xy$-plane (see Fig. 14)

$$ \textstyle\begin{array}{l} x ( t ) = r ( \beta )\cos ( \beta ), \\ y ( t ) = r ( \beta )\sin ( \beta ), \end{array} $$

(40)

where

$$ r ( \theta ) = \psi + \gamma \beta ( t ) $$

(41)

(with $\psi$ and $\gamma$ related to the values assumed in the starting and final positions). In turn, $\beta ( t )$ is defined as a 5th-degree polynomial, rest-to-rest motion law from $1.57~\text{rad}$ to $26.70~\text{rad}$ (i.e., four revolutions are considered) with a motion time of $12~\text{s}$ (the test also includes a rest interval of $1~\text{s}$ both at the beginning and at the ending). The displacement along the z-axis is defined as a 5th-degree polynomial, rest-to-rest motion law from $- 1.5~\text{m}$ to $- 0.5~\text{m}$.

Fig. 14

Planar projection of the path tracking responses with spiral reference: rigid model (a), flexible cables with collocated control (b), flexible cables with noncollocated control (c)

Such a path sometimes goes outside the static workspace, which is a condition that is rarely considered in the literature. Additionally, it almost reaches the bounds of the dynamic workspace defined as the set of all the end-effector poses and accelerations for which all cables are in tension [47], and therefore sometimes its exact tracking would require tensions that would be smaller than the lower bound on the feasible tensions. These features lead to a very challenging test case for validating the effectiveness of the proposed control scheme, since ensuring bounded tensions, despite the unfeasible reference adopted, is a duty of the proposed control scheme.

Path tracking responses are reported both in Fig. 14 by projecting the path in a $xy$-plane and in Fig. 15 through a three-dimensional representation. Both figures clearly show that a very precise contouring is ensured by the proposed control architectures since the actual and the reference paths are almost overlapped.

Fig. 15

Spatial path tracking responses with spiral reference: rigid model (a), flexible cables with collocated control (b), flexible cables with noncollocated control (c)

A more detailed evaluation of the path tracking capability is provided by Fig. 16 that shows the three-dimensional contour errors. Taking into account the rigid model response, the maximum value is equal to $8.2~\text{mm}$ and the RMS value is just $2.8~\text{mm}$. On the other hand, considering the flexible model outcome, if the collocated control scheme is considered, then its maximum and RMS values are equal to $12.6~\text{mm}$ and $7.2~\text{mm}$, respectively, while if the noncollocated architecture is taken into account, then the maximum and RMS values are equal to $8.3~\text{mm}$ and $2.8~\text{mm}$, respectively. As in the previous test, in the presence of a collocated controller, the initial and final contour errors are greater than zero because of the unmeasured static deflection due to the cable flexibility; this issue is completely solved if the noncollocated control scheme is considered. Indeed, this latter allows to achieve a contour error that is almost equal to the one obtained with the rigid cables. Apart from such static deflection component characterizing the collocated architecture, very small error in contouring the path is achieved with both control schemes despite the severe lower bound on the feasible cable tensions, confirming that they represent both good solutions for real-time path tracking in CDPRs with axially-flexible cables.

Fig. 16

Spatial contour errors with spiral reference: rigid model (a), flexible cables with collocated control (b), flexible cables with noncollocated control (c)

Finally, the commanded cable tensions are displayed in Fig. 17. Once again, the bounds are satisfied and smooth change tensions are obtained as required in the controller design.

Fig. 17

Cable tensions with spiral reference: rigid model (a), flexible cables with collocated control (b), flexible cables with noncollocated control (c)

It should be noted that if this test is performed through the two benchmark controllers discussed in Sect. 4.2.4, then severe increases of the contour error are achieved together with an oscillating behavior of the cable tensions. These results are not shown since they recall those already proposed in Sect. 4.2.4.

4.2.6 Stability robustness margins

This section evaluates the robustness of the stability of the obtained closed-loop system against gain and/or phase variations in the system to be controlled. Classical stability margins of control theory, such as phase and gain margins, take into account model mismatches by considering gain and phase perturbations in the closed-loop system in an independent manner. However, “real systems differ from their mathematical models in both magnitude and phase” [48], therefore simultaneous perturbations are here considered thanks to the exploitations of the disk margin approach [48]. Since gain and phase perturbations are considered acting simultaneously on the closed-loop system, this approach could lead to smaller stability margins compared to the classical approach, therefore leading to a more reliable robustness evaluation. Indeed, a dynamic model could be characterized by large gain and phase margins considering the classical approach, leading to thinking that the real system could be highly robust but, actually, a small combination of gain and phase perturbations could cause instability, underlying the limitations of the classical approach.

Additionally, given the MIMO nature of studied system, and CDPRs in general, two possible paths can be followed to evaluate the robustness of the closed-loop system when the disk margin method is considered: “loop-at-a-time” margins and “multiloop” margins. The former represents a typical extension of classical margins for MIMO systems, and it consists of perturbing each feedback channel singularly, while the latter corresponds to the disk margin technique applied to MIMO systems, where all feedback channels are perturbed simultaneously. However, the “loop-at-a-time” analysis is not able to capture the effect of simultaneous perturbations occurring in multiple channels and, for this reason, it can provide overly optimistic robustness parameters. To overcome this limitation, the “multiloop” technique is exploited in this paper, which leads to smaller stability margins compared to the previous mentioned analysis, but with a higher level of reliability.

Since the MPC-EI algorithm is applied to both rigid and flexible robot in the same manner (i.e., by considering the subsystem made by the end-effector whose control inputs are the cable tensions and whose outputs are the Cartesian coordinates of the end-effector), the evaluation of the robustness of the MPC-EI alone does not depend on the cable dynamics. Additionally, if ideal sensors are assumed for both the control architectures, then collocated and noncollocated controls have the same robustness margins. To focus on just the MPC-EI, here the sensor model is not accounted for. In this way, the robustness sported by such a control action, which should be adequately large to ensure stability even in the presence of sensor and cable dynamics, is evaluated.

Since the controller is position-dependent, due to the nonlinear dynamics of the robot under investigation, local analysis of the robustness margins is performed by linearizing the model of closed-loop system along the performed trajectory. In particular, the spiral path of Sect. 4.2.5 is considered since it covers the largest workspace among the three test cases presented.

The results are summarized in Fig. 18, which shows the relationship between stability margins and frequency perturbing all system states (end-effector Cartesian position and speed). It can be noticed that the minimum gain margin is $6.2~\text{dB}$, while the minimum phase margin is $37.9^{\circ}$. Remembering that both gain and phase perturbations are here applied simultaneously in a “multiloop” manner, it can be concluded that the closed-loop system presents high robustness with stability margins that are reliable for a real test case. Additionally, it should be noted that the smallest gain margins are obtained in the “low-frequency” range, where the effect of the sensor lag is negligible.

Fig. 18

Frequential behavior of gain and phase margins with spiral reference

This aspect has been indirectly seen thanks to the results reported in the different test cases, where model mismatches were included through the dynamics of the current loop controllers and of the noisy transducers and in the performance robustness analysis provided in Sect. 4.2.2.

To further stress the robustness of the closed-loop system under investigation, the same disk-margin approach has been performed by considering different values of the main tuning parameters of the model predictive control algorithm: prediction horizon $N_{p}$ (ranging from 50 to 200), control horizon $N_{c}$ (ranging from 2 to $N_{p}$), and the diagonal, input weighing matrix $\mathbf{R}_{\boldsymbol{\Delta} \mathbf{u}}$ (ranging from $1 \times 10^{ - 2}\mathbf{I}$ to $1 \times 10^{ - 4}\mathbf{I}$). The case $N_{c} = 1$ is not considered since its robustness margins approach zero, thus resulting in an almost-unstable response. The outcome of this evaluation is reported in Fig. 19, where it can be noticed that the robustness of the closed-loop system, both in terms of gain and phase margins, increases as long as the prediction horizon increases and the value of the entries of the diagonal input weighing matrix decreases. On the other hand, the effect of performances of these two parameters should be carefully accounted for. Firstly, it should be considered that when relatively long prediction horizons are considered, larger mismatches between the predicted output and the real one could occur due to the local linearization of the local input matrix of the state-space model used in the prediction. Secondly, relatively low values of the input weighing matrix could lead to very high feedback control gains that could amplify the noise coming from the measurements. The tuning proposed in this paper is therefore a trade-off between all these conflicting requirements.

Fig. 19

Behavior of gain (a) and phase (b) margins with respect to prediction horizon, control horizon, and input weighing matrix in the presence of spiral reference

5 Conclusions

This paper proposes a novel controller architecture for path tracking control in CDPRs that exploits the idea of model predictive control (MPC). To handle the nonlinear dynamic model of a CDPR with a small computational effort for boosting the real-time control, two control actions have been included. The first action computes positive and bounded cable tensions through a constrained nonlinear (pose-dependent) MPC with embedded integrator (i.e., the “velocity-form model”) that minimizes a performance index that includes the error in tracking the reference and the tension variation. The second control action translates the optimal tensions into the required motor torques and hence into commanded currents for current loops of the motor. The presence of penalizations on large variations in time of the command tensions, together with bounds on the tensions and their variations (and hence on their time derivatives), allows effectively exploiting the proposed control scheme to control CDPRs and CSPRs with axially-flexible cables without the need of a model explicitly representing such an elastic behavior. Two different control architectures are proposed: a collocated scheme that exploits the measurement of the motor rotation and kinematically estimates the end-effector position and speed and a noncollocated one that exploits direct measurement of the end-effector position. The application of the controller to the model of a CSPR (with a lumped end-effector) with very elastic cables, whose axial stiffness has been taken by the literature, shows that an almost-negligible deterioration of the path tracking performances is achieved. In particular, the noncollocated scheme also compensates for the quasi-static deflection that the collocated one is not able to control. The analysis of the computational effort shows that, although optimizing the code was not the goal of the paper, the CPU time at each time step is remarkably smaller than the time step of the control loop.

To summarize, the following novel contributions are proposed in this paper:

• Two control architectures are proposed to handle cable axial flexibility, without the need of including it into the model used for controller design, by penalizing and, also limiting with constraints, the tension derivatives.

• A modeling approach of cable axial flexibility inspired by the “penalty formulation” approach is proposed to provide a novel and more general formulation than those usually adopted in the literature of CDPRs.

• A rigorous frame is proposed to investigate the controller performances by taking advantage of some tools of control theory and of multibody dynamics, such as:

  • Stability robustness analysis by exploiting the recently introduced tool of disk margin and its relationship with the controller parameters.

  • Performance robustness analysis by exploiting a Monte Carlo analysis with random perturbations.

  • Analysis of the positive controllability.

  • Analysis of the computational effort of the proposed control scheme.

Appendix

1.1 A.1 Analysis of the positive controllability of CSPRs

A system is “positive output controllable” (POC) if, for any initial state and final desired output, the system can be driven to such a final condition through a sequence of nonnegative control actions in a finite time [49]. The necessary and sufficient condition of positive output controllability is formulated in “Theorem 1” of [41], which states that a continuous linear time invariant (LTI) system is POC if and only if there is no nonzero vector $\mathbf{v}\in \mathbb{R}^{3}$ such that

$$ \mathbf{v}^{T}\mathbf{C}_{\mathbf{c}}e^{\mathbf{A}_{\mathbf{c}}t}\mathbf{B}_{\mathbf{c}} ( \mathbf{p} )\mathbf{u} \le 0 ,\quad \forall t > 0,\ \forall \mathbf{u} \ge 0, $$

(42)

recalling that $\mathbf{A}_{\mathbf{c}}, \mathbf{B}_{\mathbf{c}} ( \mathbf{p} ), \mathbf{C}_{\mathbf{c}}$ are the state-space matrices defined in Eq. (16), $\mathbf{u}$ is the vector whose entries are the three cable tensions $t$ is the time. It is easy to prove that Eq. (16) leads to the following matrix exponential (with $\mathbf{I}\in \mathbb{R}^{6\times 6}$):

$$ e^{\mathbf{A}_{\mathbf{c}}t} = \mathbf{I} + \mathbf{A}_{\mathbf{c}}t. $$

(43)

By considering that $\mathbf{C}_{\mathbf{c}}\mathbf{I} \mathbf{B}_{\mathbf{c}} ( \mathbf{p} ) = \mathbf{0}$ and that $\mathbf{C}_{\mathbf{c}}\mathbf{A}_{\mathbf{c}}t \mathbf{B}_{\mathbf{c}} ( \mathbf{p} ) = - \frac{t}{m}\mathbf{V}(\mathbf{p})$ ($m$ is the mass of the end-effector, while $\mathbf{V} ( \mathbf{p} )$ is the matrix containing the unit vectors in the directions of the cables, as defined in Eq. (8)), then the condition in Eq. (42) can be reformulated as follows:

$$ - \frac{t}{m}\mathbf{v}^{T}\mathbf{V} ( \mathbf{p} ) \mathbf{u} \le 0. $$

(44)

By exploiting the definition of the inner product between two vectors, Eq. (44) can be written as

$$ - \frac{t}{m} \Vert \mathbf{v} \Vert \bigl\Vert \mathbf{V} ( \mathbf{p} )\mathbf{u} \bigr\Vert \cos ( \gamma ) \le 0, $$

(45)

where $\Vert \cdot \Vert$ denotes the norm of a vector, while $\gamma \in\mathbb{R}$ is the angle between the two vectors. The parameters $t, m, \Vert \mathbf{v} \Vert , \Vert \mathbf{V} ( \mathbf{p} )\mathbf{u} \Vert$ are positive scalars by definition. Therefore, the positive output controllability condition in Eq. (45) is satisfied only when $\cos ( \gamma ) \ge 0$. Given the arbitrariness of vector $\mathbf{v}$, at least one selection of $\mathbf{v}$ leading to $\cos ( \gamma ) \ge 0$ does exist and, as a consequence, the studied system is not POC.

1.2 A.2 Inclusion of the constraints of the feasible tensions

Constraints on the magnitude of the cable tensions are embedded in the control synthesis through lower ($\mathbf{u}_{\mathbf{min}} = T_{\min} \left [ \begin{array}{c@{\ \ }c@{\ \ }c} 1 & 1 & 1 \end{array} \right ]^{T}\in \mathbb{R}^{3}$) and upper bounds ($\mathbf{u}_{\mathbf{max}} = T_{\max} \left [ \begin{array}{c@{\ \ }c@{\ \ }c} 1 & 1 & 1 \end{array} \right ]^{T}\in \mathbb{R}^{3}$) on the feasible control input $\mathbf{u}(k)\in \mathbb{R}^{3}$, as mentioned in Sect. 3.2.4, defined through the element-wise inequality

$$ \mathbf{u}_{\mathbf{min}} \le \mathbf{u}(k) \le \mathbf{u}_{\mathbf{max}}. $$

(46)

Since the proposed paper uses the formulation with embedded integrator, the constraints in Eq. (46) should be translated into bounds on the difference control signal $\boldsymbol{\Delta} \mathbf{u}(k)$ and therefore on $\boldsymbol{\Delta} \mathbf{u}_{\mathbf{N}_{\mathbf{c}}}\in \mathbb{R}^{3 N_{c}}$. By defining vector $\mathbf{u}_{\mathbf{N}_{\mathbf{c}}}\in \mathbb{R}^{3 N_{c}}$ as follows:

$$ \mathbf{u}_{\mathbf{N}_{\mathbf{c}}} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \mathbf{u}(k) & \mathbf{u}(k + 1) & \cdots & \mathbf{u}(k + N_{c} - 1) \end{array}\displaystyle \right ]^{T}, $$

(47)

the relationship between $\mathbf{u}_{\mathbf{N}_{\mathbf{c}}}$, $\boldsymbol{\Delta} \mathbf{u}_{\mathbf{N}_{\mathbf{c}}}$, and $\mathbf{u}(k - 1)$ is established

$$ \mathbf{u}_{\mathbf{N}_{\mathbf{c}}} = \mathbf{C}_{\mathbf{1}}\mathbf{u}(k - 1) + \mathbf{C}_{\mathbf{2}}\boldsymbol{\Delta} \mathbf{u}_{\mathbf{N}_{\mathbf{c}}}, $$

(48)

where matrices $\mathbf{C}_{\mathbf{1}}\in \mathbb{R}^{3 N_{c} \times 3}$ and $\mathbf{C}_{\mathbf{2}}\in \mathbb{R}^{3 N_{c} \times 3 N_{c}}$ are defined as

$$ \mathbf{C}_{\mathbf{1}} = \left [ \textstyle\begin{array}{c} \mathbf{I}_{3} \\ \mathbf{I}_{3} \\ \vdots \\ \mathbf{I}_{3} \end{array}\displaystyle \right ], \qquad \mathbf{C}_{\mathbf{2}} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \mathbf{I}_{3} & \mathbf{0}_{3} & \cdots & \mathbf{0}_{3} \\ \mathbf{I}_{3} & \mathbf{I}_{3} & \cdots & \mathbf{0}_{3} \\ \vdots & \vdots & \vdots & \vdots \\ \mathbf{I}_{3} & \mathbf{I}_{3} & \cdots & \mathbf{I}_{3} \end{array}\displaystyle \right ]. $$

(49)

Therefore, input constraints along the control horizon can be imposed:

$$ \mathbf{u}_{\mathbf{N}_{\mathbf{c}} - \mathbf{min}} \le \mathbf{C}_{\mathbf{1}}\mathbf{u}(k - 1) + \mathbf{C}_{\mathbf{2}}\boldsymbol{\Delta} \mathbf{u}_{\mathbf{N}_{\mathbf{c}}} \le \mathbf{u}_{\mathbf{N}_{\mathbf{c}} - \mathbf{max}}, $$

(50)

with vectors $\mathbf{u}_{\mathbf{N}_{\mathbf{c}} - \mathbf{min}}\in \mathbb{R}^{3 N_{c}}$ and $\mathbf{u}_{\mathbf{N}_{\mathbf{c}} - \mathbf{max}}\in \mathbb{R}^{3 N_{c}}$ defined as follows:

$$ \mathbf{u}_{\mathbf{N}_{\mathbf{c}} - \mathbf{min}} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \mathbf{I}_{3} & \mathbf{I}_{3} & \cdots & \mathbf{I}_{3} \end{array}\displaystyle \right ]^{T} \mathbf{u}_{\mathbf{min}},\qquad \mathbf{u}_{\mathbf{N}_{\mathbf{c}} - \mathbf{max}} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \mathbf{I}_{3} & \mathbf{I}_{3} & \cdots & \mathbf{I}_{3} \end{array}\displaystyle \right ]^{T}\mathbf{u}_{\mathbf{max}}. $$

(51)

Finally, by rearranging all these inequalities, the constraints on the input control $\boldsymbol{\Delta} \mathbf{u}_{\mathbf{N}_{\mathbf{c}}}$ are written in the following abstract form that is suitable for inclusion within the MPC design problem:

$$ \mathbf{M}_{\mathbf{u}}\boldsymbol{\Delta} \mathbf{u}_{\mathbf{N}_{\mathbf{c}}} \le \boldsymbol{\gamma}_{\mathbf{u}}, $$

(52)

with $\mathbf{M}_{\mathbf{u}}\in \mathbb{R}^{6 N_{c} \times 3 N_{c}}$ and $\boldsymbol{\gamma}_{\mathbf{u}}\in \mathbb{R}^{6 N_{c}}$ defined as

$$ \mathbf{M}_{\mathbf{u}} = \left [ \textstyle\begin{array}{c} - \mathbf{C}_{\mathbf{2}} \\ \mathbf{C}_{\mathbf{2}} \end{array}\displaystyle \right ], \qquad \boldsymbol{\gamma}_{\mathbf{u}} = \left [ \textstyle\begin{array}{c} - \mathbf{u}_{\mathbf{N}_{\mathbf{c}} - \mathbf{min}} + \mathbf{C}_{\mathbf{1}}\mathbf{u}(k - 1) \\ \mathbf{u}_{\mathbf{N}_{\mathbf{c}} - \mathbf{max}} - \mathbf{C}_{\mathbf{1}}\mathbf{u}(k - 1) \end{array}\displaystyle \right ] . $$

(53)

1.3 A.3 Inclusion of the constraints of the allowable tension derivatives

Rather than using the derivatives, the difference tensions can be equivalently adopted and bounded by lower ($\boldsymbol{\Delta} \mathbf{u}_{\mathbf{min}} \,{=}\, \Delta T_{\min} \left [ \begin{array}{c@{\ \ }c@{\ \ }c} 1 & 1 & 1 \end{array} \right ]^{T}\in \mathbb{R}^{3}$) and upper ($\boldsymbol{\Delta} \mathbf{u}_{\mathbf{max}} = \Delta T_{\max} \left [ \begin{array}{c@{\ \ }c@{\ \ }c} 1 & 1 & 1 \end{array} \right ]^{T}\in \mathbb{R}^{3}$) bounds for all the cables. These constraints are translated into element-wise constraints on the control input along the control horizon as

$$ \boldsymbol{\Delta} \mathbf{u}_{\mathbf{N}_{\mathbf{c}} - \mathbf{min}} \le \boldsymbol{\Delta} \mathbf{u}_{\mathbf{N}_{\mathbf{c}}} \le \boldsymbol{\Delta} \mathbf{u}_{\mathbf{N}_{\mathbf{c}} - \mathbf{max}}, $$

(54)

where $\boldsymbol{\Delta} \mathbf{u}_{\mathbf{N}_{\mathbf{c}} - \mathbf{min}}\in \mathbb{R}^{3 N_{c}}$ and $\boldsymbol{\Delta} \mathbf{u}_{\mathbf{N}_{\mathbf{c}} - \mathbf{max}}\in \mathbb{R}^{3 N_{c}}$ are defined as

$$ \boldsymbol{\Delta} \mathbf{u}_{\mathbf{N}_{\mathbf{c}} - \mathbf{min}} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \mathbf{I}_{3} & \mathbf{I}_{3} & \cdots & \mathbf{I}_{3} \end{array}\displaystyle \right ]^{T}\boldsymbol{\Delta} \mathbf{u}_{\mathbf{min}},\qquad \boldsymbol{\Delta} \mathbf{u}_{\mathbf{N}_{\mathbf{c}} - \mathbf{max}} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \mathbf{I}_{3} & \mathbf{I}_{3} & \cdots & \mathbf{I}_{3} \end{array}\displaystyle \right ]^{T}\boldsymbol{\Delta} \mathbf{u}_{\mathbf{max}}. $$

(55)

Finally, to include these constraints in the MPC algorithm, they are rearranged in compact matrix form

$$ \mathbf{M}_{\boldsymbol{\Delta} \mathbf{u}}\boldsymbol{\Delta} \mathbf{u}_{\mathbf{N}_{\mathbf{c}}} \le \boldsymbol{\gamma}_{\boldsymbol{\Delta} \mathbf{u}}, $$

(56)

where $\mathbf{M}_{\boldsymbol{\Delta} \mathbf{u}}\in \mathbb{R}^{6 N_{c} \times 3 N_{c}}$ and $\boldsymbol{\gamma}_{\boldsymbol{\Delta} \mathbf{u}}\in \mathbb{R}^{6 N_{c}}$ are expressed as

$$ \mathbf{M}_{\boldsymbol{\Delta} \mathbf{u}} = \left [ \textstyle\begin{array}{c} - \mathbf{I}_{3N_{c}} \\ \mathbf{I}_{3N_{c}} \end{array}\displaystyle \right ], \qquad \boldsymbol{\gamma}_{\boldsymbol{\Delta} \mathbf{u}} = \left [ \textstyle\begin{array}{c} - \boldsymbol{\Delta} \mathbf{u}_{\mathbf{N}_{\mathbf{c}} - \mathbf{min}} \\ \boldsymbol{\Delta} \mathbf{u}_{\mathbf{N}_{\mathbf{c}} - \mathbf{max}} \end{array}\displaystyle \right ]. $$

(57)