A new perspective towards decomposition of the generalized inertia matrix of multibody systems

Abstract

This paper presents a new perspective into the decomposition of the Generalized Inertia Matrix (GIM) of multibody systems with open kinematic architecture, serial or tree-type. Links and kinematic pairs are the two constituting elements of multibody systems. In this work, we propose to decompose a multi-branch multibody system into several kinematic modules. Each module is a set of serially connected links like a serial-chain system. Such a description allows one to obtain a block decomposition $\bar{\mathbf{U}}\bar{\mathbf{D}}\bar{\mathbf{U}}^{T}$ of the GIM where $\bar{\mathbf{U}}$ and $\bar{\mathbf{D}}$ are the block upper-triangular and diagonal matrices, respectively. The results provide a recursive inverse of the GIM on module-level. Many new perspectives leading to macroscopic purview of the complex multibody systems are provided. Empowered with the proposed decomposition, an inter- and intra-modular efficient and numerically stable recursive dynamics algorithm for forward dynamics and simulation was possible. While recursive expressions are derived for a four degree-of-freedom gripper, numerical results are shown for a spatial biped.

Appendix A

The inter- and intra-modular kinematic constraints leading to the module-level DeNOC matrices are obtained in Appendices A.1 and A.2, respectively. Appendix A.3 provides an illustration of the recursive block inverse of $\bar{\mathbf{U}}$. Appendix A.4 presents a numerical validation of the decomposed GIM, whereas the steps of the forward dynamics algorithm are provided in Appendix A.5.

1.1 A.1 Intra-modular velocity constraints

As mentioned in the beginning of Sect. 2, module $i$, for $i= 1, \ldots, s$, in a tree-type system contains only serially connected links. Let us consider the $k$th link in the $i$th module, denoted #$k^{i}$, connected to the link #$(k -1)^{i}$, by a 1-DOF revolute or prismatic joint $k^{i}$, as shown in Fig. 11. The six-dimensional vector of twist associated with the angular velocity, $\boldsymbol{\omega}_{k^{i}}$, and linear velocity, $\dot{\mathbf{o}}_{k^{i}}$, of the origin of #$k^{i}$ is defined as $\mathbf{t}_{k^{i}} \equiv [\begin{array}{c@{\ }c} \boldsymbol{\omega}_{k^{i}}^{T} & \dot{\mathbf{o}}_{k^{i}}^{T} \end{array}]^{T}$. Next, the twist of #$k^{i}$, $\mathbf{t}_{k^{i}}$, can be written in terms of the twist of #$(k-1)^{i}$, $\mathbf{t}_{(k - 1)^{i}}$, as

$$ \mathbf{t}_{k^{i}} = \mathbf{A}_{k^{i},(k - 1)^{i}}\mathbf{t}_{(k - 1)^{i}} + \mathbf{p}_{k^{i}}\dot{\theta}_{k^{i}}. $$

(A.1)

In Eq. (A.1), $\dot{\theta}_{k^{i}}$ is the time rate of change of the angular or translational displacement of the $k$th joint depending on the type of joint, i.e., revolute or prismatic, respectively. The matrix $\mathbf{A}_{k^{i},(k - 1)^{i}}$ is the $6\times6$ twist-propagation matrix, and $\mathbf{p}_{k^{i}}$ is the six-dimensional join motion-propagation vector. They are given by

$$ \mathbf{A}_{k^{i},(k - 1)^{i}} \equiv \left[ \textstyle\begin{array}{c@{\quad}c} \mathbf{1} & \mathbf{O} \\ \tilde{\mathbf{a}}_{k^{i},(k - 1)^{i}} & \mathbf{1} \end{array}\displaystyle \right], \quad\mbox{and}\quad \mathbf{p}_{k^{i}} \equiv \left\{ \textstyle\begin{array}{l@{\quad}l} \left[ \textstyle\begin{array}{c} \mathbf{e}_{k^{i}}\\ \mathbf{0} \end{array}\displaystyle \right], &\mbox{if joint is revolute}, \\ \left[ \textstyle\begin{array}{c} \mathbf{0} \\ \mathbf{e}_{k^{i}} \end{array}\displaystyle \right], & \mbox{if joint is prismatic} \end{array}\displaystyle \right. $$

(A.2)

where $\tilde{\mathbf{a}}_{k^{i},(k - 1)^{i}}$ is the $3\times3$ cross-product tensor associated with vector $\mathbf{a}_{k^{i},(k - 1)^{i}}$, and $\mathbf{e}_{k^{i}}$ is the unit vector along the axis of rotation or translation of the joint $k^{i}$. Next, the vectors of module-twist and the independent module-joint-rates for the $n^{i}$-coupled links of the $i$th serial module are defined as

$$ \bar{\mathbf{t}}_{i} \equiv \left[ \textstyle\begin{array}{c} \mathbf{t}_{1^{i}} \\ \vdots\\ \mathbf{t}_{k^{i}} \\ \vdots\\ \mathbf{t}_{n^{i}} \end{array}\displaystyle \right] \quad\mbox{and}\quad \dot{\bar{\mathbf{q}}}_{i} \equiv \left[ \textstyle\begin{array}{c} \dot{\theta}_{1^{i}}\\ \vdots\\ \dot{\theta}_{k^{i}} \\ \vdots\\ \dot{\theta}_{n^{i}} \end{array}\displaystyle \right] $$

(A.3)

where $\bar{\mathbf{t}}_{i}$ and $\dot{\bar{\mathbf{q}}}_{i}$ are the $6n^{i}$- and $n^{i}$-dimensional vectors, respectively. Substituting Eq. (A.1) into Eq. (A.3), for $k^{i} =1^{i}, \ldots,n^{i}$, the expression for the generalized twist of a serial module, $\bar{\mathbf{t}}_{i}$, is obtained [10]:

$$ \bar{\mathbf{t}}_{i} = \bar{\mathbf{N}}_{i}\dot{\bar{\mathbf{q}}}_{i} \quad \mbox{where}\ \bar{\mathbf{N}}_{i} = \bar{\mathbf{N}}_{i,l}\bar{\mathbf{N}}_{i,d}. $$

(A.4)

In Eq. (A.4), $6n^{i} \times6n^{i}$ and $6n^{i} \times n^{i}$ matrices $\bar{\mathbf{N}}_{i,l}$ and $\bar{\mathbf{N}}_{i,d}$ are given by

$$ \begin{aligned} \bar{\mathbf{N}}_{i,l} &\equiv \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \mathbf{1} & &\mathbf{O} & &\cdots & \mathbf{O} \\ \mathbf{A}_{2^{i},1^{i}} & { \ddots} &\mathbf{1} & &\ddots & \vdots\\ &\ddots&&&&\\ \vdots && \mathbf{A}_{k^{i},(k - 1)^{i}} && \ddots & \mathbf{O}\\ &&&\ddots&&\\ \mathbf{A}_{n^{i},1^{i}} & &\cdots & &\mathbf{A}_{n^{i},(n - 1)^{i}} & \mathbf{1} \end{array}\displaystyle \right] \quad\mbox{and}\\ \bar{\mathbf{N}}_{i,d} &\equiv \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \mathbf{p}_{1^{i}} & &&& \mathbf{0}'\mathrm{s}\\ & { \ddots}&&&\\ && \mathbf{p}_{k^{i}} &&\\ &&&{ \ddots}&\\ \mathbf{0}'\mathrm{s}&&& & \mathbf{p}_{n^{i}} \end{array}\displaystyle \right]. \end{aligned} $$

(A.5)

The matrices $\bar{\mathbf{N}}_{i,l}$ and $\bar{\mathbf{N}}_{i,d}$ are referred here as the Decoupled Natural Orthogonal Complement (DeNOC) matrices of the serial-module, which are nothing but those reported in [10] for a serial robot.

Fig. 11

Links #$k^{i}$ and $\#(k-1)^{i}$ coupled by joint $k^{i}$ in $i$th module

1.2 A.2 Inter-modular velocity constraints

It is worth noting that Eq. (A.4) represents the twists of the links in the $i$th module if it emanates from the ground. However, in a tree-type system, each module, other than the base, is a child module, e.g., $M_{i}$ in Fig. 1(b), which contains serially connected links and emerges from the last link of its parent module $M_{\beta}$. Hence, the velocity constraints between the modules, i.e., at inter-modular level, will be derived in this section as an extension of the expression derived in Eq. (A.4). For the module $M_{i}$, the $6n^{i}$-dimensional vector of module-twist, $\bar{\mathbf{t}}_{i}$, which has $n^{i}$ link twists, and the $n^{i}$-dimensional vector of module-joint-rate, $\dot{\bar{\mathbf{q}}}_{i}$, having $n^{i}$ joint rates are defined in Eq. (A.3). Next, it is shown that the module-twist $\bar{\mathbf{t}}_{i}$, for $M_{i}$, can be written in terms of the module-twist $\bar{\mathbf{t}}_{\beta}$ (or $\bar{\mathbf{t}}_{\beta_{i}}$) of its parent $M_{\beta}$ as

$$ \bar{\mathbf{t}}_{i} = \bar{\mathbf{A}}_{i,\beta} \bar{\mathbf{t}}_{\beta_{i}} + \bar{\mathbf{N}}_{i}\dot{\bar{\mathbf{q}}}_{i} $$

(A.6)

where $\bar{\mathbf{A}}_{i,\beta}$ and $\bar{\mathbf{N}}_{i}$ are the $6n^{i} \times6n^{\beta}$ module-twist propagation and $6n^{i} \times n^{i}$ module-joint-motion propagation matrices, respectively, which are given by

$$ \begin{aligned} \bar{\mathbf{A}}_{i,\beta} &\equiv \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \mathbf{O}& \cdots & \mathbf{O} & \mathbf{A}_{1^{i},n^{\beta}} \\ \vdots&&\vdots&\vdots\\ \mathbf{O}& & \mathbf{O}&\mathbf{A}_{k^{i},n^{\beta}} \\ \vdots&&\vdots&\vdots\\ \mathbf{O} & \cdots & \mathbf{O} & \mathbf{A}_{n^{i},n^{\beta}} \end{array}\displaystyle \right] \quad\mbox{and}\\ \bar{\mathbf{N}}_{i} &\equiv \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \mathbf{p}_{1^{i}} && \mathbf{0} & &\cdots & \mathbf{0} \\ &\ddots&&&&\\ \mathbf{A}_{2^{i},1^{i}}\mathbf{p}_{1^{i}} & & \mathbf{p}_{(k - 1)^{i}} & &\ddots & \vdots \\ &\ddots&&&&\\ \vdots & & \mathbf{A}_{k^{i},(k - 1)^{i}}\mathbf{p}_{(k - 1)^{i}} && \ddots & \mathbf{0} \\ &&&\ddots&&\\ \mathbf{A}_{n^{i},1^{i}}\mathbf{p}_{1^{i}} & &\cdots & & \mathbf{A}_{n^{i},(n - 1)^{i}}\mathbf{p}_{(n - 1)^{i}} & \mathbf{p}_{n^{i}} \end{array}\displaystyle \right]. \end{aligned} $$

(A.7)

In Eq. (A.7), $\bar{\mathbf{A}}_{i,\beta}$ propagates the twist of the parent module ($\beta$th) to the child module ($i$th); the last column contains the twist propagation matrix from the $n$th link of the $\beta$th module wherefrom the $i$th module emanates, to the different links of the $i$th module. Matrix $\mathbf{A}_{k^{i},n^{\beta}}$ in the expression of $\bar{\mathbf{A}}_{i,\beta}$ denotes the $6\times6$ twist-propagation matrix from the twist of link #$n^{\beta}$ (last link in the $\beta$th module) in module $M_{\beta}$ to the twist of link #$k^{i}$ in module $M_{i}$. Moreover, $\mathbf{A}_{k^{i},(k - 1)^{i}}$ and $\mathbf{p}_{k^{i}}$ are defined in Eq. (A.2). Next, considering the links and joints of all the modules, the generalized twist vector, $\mathbf{t}$, consisting of all module-twists, and the generalized joint-rate vector, $\dot{\mathbf{q}}$, consisting of all module-joint-rates are defined as

$$ \mathbf{t} \equiv \left[ \textstyle\begin{array}{c} \bar{\mathbf{t}}_{1}\\ \vdots \\ \bar{\mathbf{t}}_{s} \end{array}\displaystyle \right] \quad\mbox{and}\quad \dot{\mathbf{q}} \equiv \left[ \textstyle\begin{array}{c} \dot{\bar{\mathbf{q}}}_{1} \\ \vdots \\ \dot{\bar{\mathbf{q}}}_{s} \end{array}\displaystyle \right]. $$

(A.8)

In Eq. (A.8), the vector of module-twists $\bar{\mathbf{t}}_{i}$ and module-joint-rates $\dot{\bar{\mathbf{q}}}_{i}$ contain link twists and joint rates, respectively, as defined in Eq. (A.3). Substituting Eq. (A.6) into Eq. (A.8), for $i = 1, \ldots, s$, the generalized twist $\mathbf{t}$ is expressed as

$$ \mathbf{t} = \bar{\mathbf{A}}\mathbf{t} + \bar{\mathbf{N}}_{d}\dot{\mathbf{q}} $$

(A.9)

where $\bar{\mathbf{A}}$ and $\bar{\mathbf{N}}_{d}$ are the $6n \times6n$ and $6n \times n$ matrices, and they are given as

$$ \begin{aligned} \bar{\mathbf{A}} &\equiv \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \mathbf{O} & &&& & \mathbf{O}'\mathrm{s} \\ &\ddots&&&&\\ \bar{\mathbf{A}}_{2,\beta} & & \mathbf{O} & & &\\ &\ddots&&&&\\ && \bar{\mathbf{A}}_{i,\beta} && \ddots & \\ &&&\ddots&&\\ \mathbf{O}'\mathrm{s} & & && \bar{\mathbf{A}}_{s,\beta} & \mathbf{O} \end{array}\displaystyle \right], \quad\mbox{and}\\ \bar{\mathbf{N}}_{d} &\equiv \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \bar{\mathbf{N}}_{1} & && &\mathbf{O}'\mathrm{s} \\ & { \ddots}&&&\\ && \bar{\mathbf{N}}_{i} &&\\ &&&\ddots&\\ \mathbf{O}'\mathrm{s} & & && \bar{\mathbf{N}}_{s} \end{array}\displaystyle \right]. \end{aligned} $$

(A.10)

In Eq. (A.10), $\beta$ in $\bar{\mathbf{A}}_{i,\beta}$ corresponds to the parent of $i$, for $i=1, \ldots,s$. Rearranging Eq. (A.10), the $6n$-dimensional generalized twist is given by

$$ \mathbf{t} = \bar{\mathbf{N}}_{l}\bar{\mathbf{N}}_{d}\dot{\mathbf{q}},\quad \mbox{where}\ \bar{\mathbf{N}}_{l} = (1 - \bar{\mathbf{A}})^{ - 1}. $$

(A.11)

The $6n \times6n$ matrix $\bar{\mathbf{N}}_{l}$ can easily be obtained

$$ \bar{\mathbf{N}}_{l} \equiv \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \mathbf{1}_{1} & & & &\\ \bar{\mathbf{A}}_{2,1} & \mathbf{1}_{2} & & \mathbf{O}'\mathrm{s}& \\ \bar{\mathbf{A}}_{3,1} & \bar{\mathbf{A}}_{3,2} & \mathbf{1}_{3} & &\\ \vdots & \vdots & \ddots & \ddots& \\ \bar{\mathbf{A}}_{s,1} & \bar{\mathbf{A}}_{s,2} & \cdots & \bar{\mathbf{A}}_{s,s - 1} & \mathbf{1}_{s} \end{array}\displaystyle \right] $$

(A.12)

where $1_{i}$ represents the $6n^{i} \times6n^{i}$ identity matrix, and $\mathbf{O}$ is the null matrix of compatible dimension. Moreover, $\bar{\mathbf{A}}_{i,j}$ and $\bar{\mathbf{N}}_{i}$ are the $6n^{i} \times6n^{j}$ module-twist propagation and the $6n^{i} \times n^{i}$ module-joint-motion propagation matrices, in line with the twist-propagation matrix and joint-motion propagation vector from one link to the neighboring link connected by a single-degree-of-freedom joint [10]. The term $\bar{\mathbf{A}}_{i,j}$, defined similar to $\bar{\mathbf{A}}_{i,\beta}$ in Eq. (A.7), propagates the twist of the $j$th module relative to the $i$th one, where $\bar{\mathbf{A}}_{j,i} \equiv \mathbf{O}$ if module $M_{j}$ does not belong to the set $\boldsymbol{\gamma}_{i}$ of all modules originating from $M_{i}$, as shown in Fig. 3. The matrices $\bar{\mathbf{N}}_{l}$ and $\bar{\mathbf{N}}_{d}$ of Eq. (A.11) are nothing but the DeNOC matrices for the multi-modular tree-type system under study, rather than the multi-link system.

1.3 A.3 An illustration of recursive block inverse of $\bar{\mathbf{U}}$

The inverse of the block upper triangular matrix $\bar{\mathbf{U}}$ can be obtained from Eq. (39) as

$$ \bar{\mathbf{U}}^{ - 1} \equiv \bar{\mathbf{U}}_{2} \cdots \bar{\mathbf{U}}_{i} \cdots \bar{\mathbf{U}}_{s} \equiv \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \mathbf{1} & \hat{\bar{\mathbf{U}}}_{1,2} & \cdots & \hat{\bar{\mathbf{U}}}_{1,s} \\ \mathbf{O} & \mathbf{1} & \ddots & \vdots \\ \vdots & \ddots & \ddots & \hat{\bar{\mathbf{U}}}_{s - 1,s} \\ \mathbf{O} & \cdots & \mathbf{O} & \mathbf{1} \end{array}\displaystyle \right]. $$

(A.13)

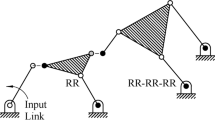
In order to comprehend recursive relationship for the block elements $\hat{\bar{\mathbf{U}}}_{i,j}$, the tree-type system should have at least three serially connected modules. The example of gripper is simple enough as it contains only two serially connected module sets, i.e., ($M_{1}, M_{2}$) and ($M_{1}, M_{3}$). Therefore, let us consider a simplest system with three serially connected modules $M_{1}$, $M_{2}$ and $M_{3}$. For such a three module system $\bar{\mathbf{U}}^{ - 1}$ is expressed as

$$ \bar{\mathbf{U}}^{ - 1} \equiv \bar{\mathbf{U}}_{2}\bar{\mathbf{U}}_{3} $$

(A.14)

where the elements of EBUTM $\bar{\mathbf{U}}_{2}$ and $\bar{\mathbf{U}}_{3}$ are obtained from Eq. (30) and the resulting matrices $\bar{\mathbf{U}}_{2}$ and $\bar{\mathbf{U}}_{3}$ are given by

$$ \bar{\mathbf{U}}_{2} = \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c} 1 & - \bar{\mathbf{N}}_{1}^{T}\bar{\mathbf{A}}^{T}_{2,1}\bar{\boldsymbol{\Psi}}_{2} \hat{\bar{\mathbf{I}}}_{2}^{ - 1} & \mathbf{O}\\ \mathbf{O} & \mathbf{1} & \mathbf{O} \\ \mathbf{O} & \mathbf{O} & \mathbf{1} \end{array}\displaystyle \right] \quad\mbox{and}\quad \bar{\mathbf{U}}_{3} = \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \mathbf{1} & \mathbf{O} & - \bar{\mathbf{N}}_{1}^{T}\bar{\mathbf{A}}^{T}_{3,1}\bar{\boldsymbol{\Psi}}_{3} \hat{\bar{\mathbf{I}}}_{3}^{ - 1}\\ \mathbf{O} & \mathbf{1} & - \bar{\mathbf{N}}_{2}^{T}\bar{\mathbf{A}}^{T}_{3,2}\bar{\boldsymbol{\Psi}}_{3} \hat{\bar{\mathbf{I}}}_{3}^{ - 1}\\ \mathbf{O} & \mathbf{O} & \mathbf{1} \end{array}\displaystyle \right]. $$

(A.15)

Substituting Eq. (A.15) into Eq. (A.14) $\mathbf{U}^{ - 1}$ is expressed as

$$ \mathbf{U}^{ - 1} = \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \mathbf{1} & - \bar{\mathbf{N}}_{1}^{T}\bar{\mathbf{A}}^{T}_{2,1}\bar{\boldsymbol{\Psi}}_{2} \hat{\bar{\mathbf{I}}}_{2}^{ - 1} & - \bar{\mathbf{N}}_{1}^{T}\hat{\bar{\mathbf{A}}}^{T}_{3,1}\bar{\boldsymbol{\Psi}}_{3} \hat{\bar{\mathbf{I}}}_{3}^{ - 1}\\ \mathbf{O} & \mathbf{1} & - \bar{\mathbf{N}}_{2}^{T}\bar{\mathbf{A}}^{T}_{3,2}\bar{\boldsymbol{\Psi}}_{3} \hat{\bar{\mathbf{I}}}_{3}^{ - 1} \\ \mathbf{O} & \mathbf{O} & \mathbf{1} \end{array}\displaystyle \right]. $$

(A.16)

The $(1,3)$ block element in Eq. (A.16) denoted $\hat{\bar{\mathbf{U}}}_{1,3}$ is the simplified expression which is obtained as follows:

$$\begin{aligned} \hat{\bar{\mathbf{U}}}_{1,3} =& - \bar{\mathbf{N}}_{1}^{T} \bar{\mathbf{A}}^{T}_{3,1} \bar{\boldsymbol{\Psi}}_{3} \hat{\bar{ \mathbf{I}}}_{3}^{ - 1} + \bar{\mathbf{N}}_{1}^{T} \bar{\mathbf{A}}^{T}_{2,1}\bar{\boldsymbol{\Psi}}_{2} \hat{\bar{ \mathbf{I}}}_{2}^{ - 1}\bar{\mathbf{N}}_{2}^{T} \bar{\mathbf{A}}^{T}_{3,2}\bar{\boldsymbol{\Psi}}_{3} \hat{\bar{ \mathbf{I}}}_{3}^{ - 1} \\ =& - \bar{\mathbf{N}}_{1}^{T} \bigl( \bar{\mathbf{A}}^{T}_{3,1} - \bar{\mathbf{A}}^{T}_{2,1} \bar{\boldsymbol{\Psi}}_{2} \hat{\bar{\mathbf{I}}}_{2}^{ - 1}\bar{ \mathbf{N}}_{2}^{T}\bar{\mathbf{A}}^{T}_{3,2} \bigr)\bar{\boldsymbol{\Psi}}_{3} \hat{\bar{\mathbf{I}}}_{3}^{ - 1} \\ =& - \bar{\mathbf{N}}_{1}^{T} \bigl( \bar{ \mathbf{A}}^{T}_{2,1}\bar{\mathbf{A}}^{T}_{3,2} - \bar{\mathbf{A}}^{T}_{2,1}\bar{\boldsymbol{\Psi}}_{2} \hat{\bar{ \mathbf{I}}}_{2}^{ - 1} \bar{\mathbf{N}}_{2}^{T} \bar{\mathbf{A}}^{T}_{3,2} \bigr)\bar{\boldsymbol{\Psi}}_{3} \hat{ \bar{\mathbf{I}}}_{3}^{ - 1} \\ =& - \bar{\mathbf{N}}_{1}^{T} \bar{\mathbf{A}}^{T}_{2,1} \bigl( \mathbf{1} - \bar{\boldsymbol{\Psi}}_{2} \hat{\bar{\mathbf{I}}}_{2}^{ - 1} \bar{\mathbf{N}}_{2}^{T} \bigr)\bar{\mathbf{A}}^{T}_{3,2}\bar{\boldsymbol{\Psi}}_{3} \hat{ \bar{\mathbf{I}}}_{3}^{ - 1} \\ =& - \bar{\mathbf{N}}_{1}^{T} \bigl( \bar{\mathbf{A}}_{3,2}\bar{\boldsymbol{\Phi}}_{2}^{T}\bar{ \mathbf{A}}_{2,1} \bigr)^{T}\bar{\boldsymbol{\Psi}}_{3} \hat{\bar{ \mathbf{I}}}_{3}^{ - 1} \quad \bigl( \mbox{where}\ \bar{ \boldsymbol{\Phi}}_{2} = \mathbf{1} - \bar{\boldsymbol{\Psi}}_{2} \hat{\bar{\mathbf{I}}}_{2}^{ - 1} \bar{\mathbf{N}}_{2}^{T} \bigr) \\ =& - \bar{\mathbf{N}}_{1}^{T} \hat{\bar{\mathbf{A}}}^{T}_{3,1}\bar{\boldsymbol{\Psi}}_{3} \hat{ \bar{\mathbf{I}}}_{3}^{ - 1}\quad \bigl( \mbox{where}\ \hat{\bar{ \mathbf{A}}}_{3,1} = \bar{\mathbf{A}}_{3,2}\bar{ \boldsymbol{\Phi}}_{2}^{T}\bar{\mathbf{A}}_{2,1} \bigr) \end{aligned}$$

(A.17)

where

$$ \hat{\bar{\mathbf{A}}}_{3,1} = \bar{\mathbf{A}}_{3,2}\bar{\boldsymbol{\Phi}}_{2}^{T}\bar{\mathbf{A}}_{2,1}. $$

(A.18)

It may be noted that, for the adjoining modules sets ($M_{2}, M_{3}$) and ($M_{1},M_{2}$), $\hat{\bar{\mathbf{A}}}_{3,2} = \bar{\mathbf{A}}_{3,2}$ and $\hat{\bar{\mathbf{A}}}_{2,1} = \bar{\mathbf{A}}_{2,1}$.

1.4 A.4 Numerical validation of the decomposed GIM of gripper

For the set of numerical values of the link masses and inertias, as given in Table 2, the GIM can be obtained for the configuration $\theta_{1^{1}} = \theta_{1^{2}} = \theta_{2^{2}} = 0$ and $\theta_{1^{3}}=90$, as

$$ \mathbf{I} = \left[ \textstyle\begin{array}{c|c@{\quad}c|c} 113.3333 & 33.3333 & 9.1667 & 1.6667 \\ \hline & 13.3333 & 4.1667 & 0 \\ & & 1.6667 & 0 \\ \hline \mathit{sym} & & & 1.6667 \end{array}\displaystyle \right] \times 10^{ - 4}. $$

(A.19)

Its decomposed block matrices $\bar{\mathbf{U}}$ and $\bar{\mathbf{D}}$, and the corresponding block inverses $\bar{\mathbf{U}}^{ - 1}$ and $\bar{\mathbf{D}}^{ - 1}$, respectively, are obtained from Eq. (34) and Eq. (58) as follows:

$$ \begin{aligned} \bar{\mathbf{U}} &= \left[ \textstyle\begin{array}{c|c@{\quad}c|c} 1 & 3.571 & - 3.428 & 1\\ \hline 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0\\ \hline 0 & 0 & 0 & 1 \end{array}\displaystyle \right], \\ \bar{\mathbf{D}} &= \left[ \textstyle\begin{array}{c|c@{\quad}c|c} 24.047 & 0 & 0 & 1 \\ \hline 0 & 13.333 & 4.166 & 0\\ 0 & 4.166 & 1.666 & 0\\ \hline 0 & 0 & 0 & 1.666 \end{array}\displaystyle \right] \times 10^{ - 4} \end{aligned} $$

(A.20)

and

$$ \begin{aligned} \bar{\mathbf{U}}^{ - 1}& = \left[ \textstyle\begin{array}{c|c@{\quad}c|c} 1 & - 3.5714 & 3.4286 & - 1 \\ \hline 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \hline 0 & 0 & 0 & 1 \end{array}\displaystyle \right], \\ \bar{\mathbf{D}}^{ - 1}& = \left[ \textstyle\begin{array}{c|c@{\quad}c|c} 0.0416 & 0 & 0 & 1 \\ \hline 0 & 0.3429 & - 0.8571 & 0 \\ 0 & - 0.8571 & 2.7429 & 0 \\ \hline 0 & 0 & 0 & 0.6 \end{array}\displaystyle \right] \times 10^{4}. \end{aligned} $$

(A.21)

It is now a simple matter to verify the correctness of the inverses by computing $\mathbf{I}^{ - 1} = \bar{\mathbf{U}}^{ - 1}\bar{\mathbf{D}}^{ - 1}\bar{\mathbf{U}}^{ - T}$ as

$$ \mathbf{I}^{ - 1} = \left[ \textstyle\begin{array}{c|c@{\quad}c|c} 0.0416 & - 0.1485 & 0.1426 & - 0.0416 \\ \hline & 0.8733 & - 1.3663 & 0.1485\\ & & 3.2317 & - 0.1426 \\ \hline \mathit{sym} & & & 0.6416 \end{array}\displaystyle \right] \times 10^{4}. $$

(A.22)

Equation (A.22) was checked against numerical result obtained using MATLAB command “inv.”

1.5 A.5 Forward dynamics algorithm for a tree-type multibody system

Steps for recursive forward dynamics algorithm [12] are shown in Table 6.

Table 6 Recursive ${O}(n)$ forward dynamics algorithm for a tree-type multibody systems [12]