Fractional calculus model of articular cartilage based on experimental stress-relaxation

Abstract

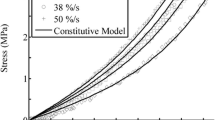
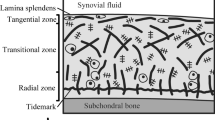
Articular cartilage is a unique substance that protects joints from damage and wear. Many decades of research have led to detailed biphasic and triphasic models for the intricate structure and behavior of cartilage. However, the models contain many assumptions on boundary conditions, permeability, viscosity, model size, loading, etc., that complicate the description of cartilage. For impact studies or biomimetic applications, cartilage can be studied phenomenologically to reduce modeling complexity. This work reports experimental results on the stress-relaxation of equine articular cartilage in unconfined loading. The response is described by a fractional calculus viscoelastic model, which gives storage and loss moduli as functions of frequency, rendering multiple advantages: (1) the fractional calculus model is robust, meaning that fewer constants are needed to accurately capture a wide spectrum of viscoelastic behavior compared to other viscoelastic models (e.g., Prony series), (2) in the special case where the fractional derivative is 1/2, it is shown that there is a straightforward time-domain representation, (3) the eigenvalue problem is simplified in subsequent dynamic studies, and (4) cartilage stress-relaxation can be described with as few as three constants, giving an advantage for large-scale dynamic studies that account for joint motion or impact. Moreover, the resulting storage and loss moduli can quantify healthy, damaged, or cultured cartilage, as well as artificial joints. The proposed characterization is suited for high-level analysis of multiphase materials, where the separate contribution of each phase is not desired. Potential uses of this analysis include biomimetic dampers and bearings, or artificial joints where the effective stiffness and damping are fundamental parameters.

Appendix

For simplicity, only a one-element fractional derivative model is developed. However, the one-element model can be generalized to include multiple elements in parallel by the principle of linear superposition. This concept is analogous to that of the more common Prony series. The constitutive equation relating stress to strain is similar to that of a standard linear viscoelastic material:

$$\begin{aligned} \biggl(1+\frac{E_0}{E_1} \biggr)\frac{d{\epsilon}}{dt} + \frac {E_0}{c_1} \epsilon= \frac{1}{E_1}\frac{d{\sigma}}{dt} + \frac {1}{c_1}\sigma, \end{aligned}$$

(A.1)

except that the dashpot is replaced with the spring-pot element

$$\begin{aligned} \frac{d\epsilon}{dt} \longleftarrow\frac{d^\alpha\epsilon }{dt^\alpha} \end{aligned}$$

(A.2)

and

$$\begin{aligned} \frac{d\sigma}{dt} \longleftarrow\frac{d^\alpha\sigma}{dt^\alpha}, \end{aligned}$$

(A.3)

leading to the constitutive equation for the fractional derivative model

$$\begin{aligned} \biggl(1+\frac{E_0}{E_1} \biggr)\frac{d^{\alpha}{\epsilon }}{dt^\alpha} + \frac{E_0}{\eta_1} \epsilon= \frac{1}{E_1}\frac {d^\alpha{\sigma}}{dt^\alpha} + \frac{1}{\eta_1}\sigma. \end{aligned}$$

(A.4)

In Eq. (A.4), the damping coefficient c ₁ has been replaced by η ₁ to reflect unit consistency. If α=1, then the constitutive model becomes the standard linear material (one-term Prony model shown in Eq. (A.1)), and the units of η ₁ collapse to those of c ₁ (Pa s). If α=0, then the spring-pot simply becomes strictly a spring, and the entire model is reduced to an equivalent linear spring. For any fractional valued α between 0 and 1, the spring-pot element has both spring and dashpot behavior.

Equation (A.4) is conveniently analyzed in the Laplace domain, which allows for the treatment of the fractional power (taking Caputo’s definition of the fractional-order derivative and assuming that the initial conditions for stress and strain can be set to zero (Podlubny 1998)):

$$\begin{aligned} \biggl[ \biggl(1+\frac{E_0}{E_1} \biggr)s^{\alpha} + \frac{E_0}{\eta _1} \biggr]\epsilon(s) = \biggl(\frac{1}{E_1}s^\alpha+ \frac {1}{\eta_1} \biggr)\sigma(s). \end{aligned}$$

(A.5)

Utilizing the elastic–viscoelastic correspondence principle (Eq. (2)), the relaxation modulus E(s) can be found from Eq. (A.5):

$$\begin{aligned} E(s) = \frac{ \bigl[ \bigl(1+\frac{E_0}{E_1} \bigr)s^{\alpha} + \frac{E_0}{\eta_1} \bigr]}{ (\frac{1}{E_1}s^\alpha+ \frac {1}{\eta_1} )}\frac{1}{s}. \end{aligned}$$

(A.6)

The relationship between the Laplace and frequency domains allows for the fractional model to be obtained:

$$\begin{aligned} E(\omega) = \frac{ \bigl[ \bigl(1+\frac{E_0}{E_1} \bigr) (i\omega )^{\alpha} + \frac{E_0}{\eta_1} \bigr]}{ [\frac{1}{E_1} (i\omega )^\alpha+ \frac{1}{\eta _1} ]} \biggl(\frac{1}{i\omega} \biggr). \end{aligned}$$

(A.7)

With some algebra, Eq. (A.7) can be reduced to

$$\begin{aligned} E(\omega) = \frac{1}{i\omega} \biggl[{E_0} + \frac{E_1 (i\omega )^{\alpha}}{ \bigl[ (i\omega )^\alpha+ \frac{E_1}{\eta_1} \bigr]} \biggr]. \end{aligned}$$

(A.8)

If required, the fractional model can be generalized to include more spring-pot elements:

$$\begin{aligned} E(\omega) =\frac{1}{i\omega} \Biggl[{E_0} + \sum _{n=1}^{\infty}\frac{E_n (i\omega )^{\alpha}}{\bigl[ (i\omega )^\alpha+ \frac{E_n}{\eta_n} \bigr]} \Biggr]. \end{aligned}$$

(A.9)

Theoretically, an infinite number of terms can be used. In practice, this number is finite. The complex modulus is found from the elastic–viscoelastic correspondence principle (Eq. (2)):

$$\begin{aligned} E^*(\omega) = E_0 + \sum _{n=1}^{\infty} \frac{E_n (i\omega )^{\alpha}}{ \bigl[ (i\omega )^\alpha+ \frac{E_n}{\eta_n} \bigr]}. \end{aligned}$$

(A.10)

Simplifications for α=1/2 (special case)

For the special case of α=1/2, the mathematics of the fractional model simplify dramatically. In the time domain, a concise solution appears in the form of a complementary error function multiplied by a decaying exponential. An analytic form of the model can be found for the frequency domain solution as well. Consider a one-term fractional model with α=1/2:

$$\begin{aligned} E^*(\omega) = E_0 + \frac{E_1 (i\omega )^{1/2}}{ \bigl[ (i\omega )^{1/2} + \frac{E_1}{\eta_1} \bigr]}. \end{aligned}$$

(A.11)

The square root of iω can be found from the generalized form of de Moivre’s theorem:

$$\begin{aligned} (i\omega)^{1/2} = \frac{\sqrt{2\omega}}{2}(1+i). \end{aligned}$$

(A.12)

Two substitutions help clarify the mathematics:

$$\begin{aligned} \beta= \frac{\sqrt{2\omega}}{2}, \end{aligned}$$

(A.13)

$$\begin{aligned} \mu_1 = \frac{E_1}{\eta_1}. \end{aligned}$$

(A.14)

Both β and μ ₁ have the units ${\rm s}^{-1/2}$. Substituting these relations into Eq. (A.11) yields

$$\begin{aligned} E^*(\omega) = E_0 + \frac{E_1\beta(1+i)}{\mu_1 + \beta(1+i)}. \end{aligned}$$

(A.15)

After algebraic manipulation and the simplification (1+i)²=2i, Eq. (A.15) is

$$\begin{aligned} E^*(\omega) = E_0 + E_1\beta \biggl[\frac{\mu_1 - (2\beta- \mu _1)i}{\mu_1^2 - 2\beta^2 i} \biggr]. \end{aligned}$$

(A.16)

Additional manipulation leads to a usable expression:

$$\begin{aligned} E^*(\omega) = E_0 + E_1\beta \biggl[\frac{\mu_1 + 2\beta}{\mu_1^2 + 2\mu_1\beta+ 2\beta^2} + \frac{ i\mu_1}{\mu_1^2 + 2\mu_1\beta + 2\beta^2} \biggr]. \end{aligned}$$

(A.17)

Reintroducing the substitution of Eq. (A.13), the derivation of the one-element CERF model is complete:

$$\begin{aligned} E^*(\omega) = E_0 + E_1 \biggl[\frac{ \bigl(\frac{\sqrt{2\omega }}{2} \bigr)\mu_1 + \omega}{\mu_1^2 + \mu_1\sqrt{2\omega} + \omega} + \frac{ i \bigl(\frac{\sqrt{2\omega}}{2} \bigr)\mu _1}{\mu_1^2 + \mu_1\sqrt{2\omega} + \omega} \biggr]. \end{aligned}$$

(A.18)

Equations (A.18) can be generalized for any number of fractional terms, although the utility of the fractional model is that few terms typically need to be used to characterize viscoelastic behavior:

$$\begin{aligned} E^*(\omega) = E_0 + \sum _{n=1}^{\infty} E_n \biggl[\frac { \bigl(\frac{\sqrt{2\omega}}{2} \bigr)\mu_n + \omega}{\mu_n^2 + \mu_n\sqrt{2\omega} + \omega} + \frac{ i \bigl(\frac{\sqrt {2\omega}}{2} \bigr)\mu_n}{\mu_n^2 + \mu_n\sqrt{2\omega} + \omega} \biggr], \end{aligned}$$

(A.19)

and if

$$\begin{aligned} E^*(\omega) = E'(\omega) + iE''(\omega), \end{aligned}$$

(A.20)

then

$$\begin{aligned} E'(\omega) = E_0 + \sum _{n=1}^{\infty} E_n \biggl[\frac { \bigl(\frac{\sqrt{2\omega}}{2} \bigr)\mu_n + \omega}{\mu_n^2 + \mu_n\sqrt{2\omega} + \omega} \biggr], \end{aligned}$$

(A.21)

$$\begin{aligned} E''(\omega) = \sum _{n=1}^{\infty} E_n \biggl[\frac{ \bigl(\frac{\sqrt{2\omega}}{2} \bigr)\mu_n}{\mu_n^2 + \mu_n\sqrt {2\omega} + \omega} \biggr]. \end{aligned}$$

(A.22)

For the fractional derivative model where α=1/2, there exists a concise time-domain solution (Szumski and Green 1991):

$$\begin{aligned} E(t) = E_0 + \sum _{n=1}^{\infty}E_n e^{ ({\mu_n}^2 t )} \mathrm{erfc}~(\mu_n \sqrt{t}), \end{aligned}$$

(A.23)

which is a decaying complementary error function multiplied by an increasing exponential. The time-domain solution is critical for fitting experimental data. The Laplace transformation of Eq. (9) is given by Szumski and Green (1991):

$$\begin{aligned} E(s) = \frac{1}{s} \Biggl[E_0 + \sum _{n=1}^{\infty} \frac {E_n\sqrt{s}}{\sqrt{s}+\mu_n} \Biggr]. \end{aligned}$$

(A.24)

Equation (A.24) and application of the elastic–viscoelastic correspondence principle allows us to relate the CERF model in the time and frequency domains, noting the connection between the Laplace and Fourier transformations (replace the Laplace variable s with the Fourier variable iω). We then arrive back at Eq. (A.19).