A Postulated Planetary Collision, the Terrestrial Planets, the Moon and Smaller Solar-System Bodies

Abstract

In a scenario produced by the Capture Theory of planetary formation, a collision between erstwhile solar-system giant planets, of masses 798.75 and 598.37 M _⊕, is simulated using smoothed-particle hydrodynamics. Due to grain-surface chemistry that takes place in star-forming clouds, molecular species containing hydrogen, with a high D/H ratio taken as 0.01, form a layer around each planetary core. Temperatures generated by the collision initiate D–D reactions in these layers that, in their turn, trigger a reaction chain involving heavier elements. The nuclear explosion shatters and disperses both planets, leaving iron-plus-silicate stable residues identified as a proto-Venus and proto-Earth. A satellite of one of the colliding planets, captured or retained by the proto-Earth core, gave the Moon; two massive satellites released into heliocentric orbits became Mercury and Mars. For the Moon and Mars, abrasion of their surfaces exposed to collision debris results in hemispherical asymmetry. Mercury, having lost a large part of its mantle due to massive abrasion, reformed to give the present high-density body. Debris from the collision gave rise to asteroids and comets, much of the latter forming an inner reservoir stretching outwards from the inner Kuiper Belt that replenishes the Oort Cloud when it is depleted by a severe perturbation. Other features resulting from the outcome of the planetary collision are the relationship of Pluto and Triton to Neptune, the presence of dwarf planets and light-atom isotopic anomalies in meteorites.

1 Introduction

Smoothed particle hydrodynamic (SPH) simulations of the Capture Theory (CT) of planet formation (Oxley and Woolfson 2004) shows that in a dense embedded cluster (Lada and Lada 2003) the tidal interaction of a compact star on either a protostar or a dense region of the star-forming cloud, stretches the diffuse material into a filament-like structure within which protoplanetary condensations form. Some of these are captured by the compact star to form a planetary family while others escape to become free-floating planets (Lucas and Roche 2000; Sumi et al. 2011). Captured protoplanets initially move away from the compact star on orbits with semi-major axes and eccentricities of order 1,000 au and 0.9, so by the time the protoplanets reach periastron they are approaching their final condensed form and are stable even when very close to the star.

The protoplanets form as above-Jeans-mass condensations in the filament and only gas-giant planets can form this way, which raises the question of how terrestrial planets formed in the Solar System. Dormand and Woolfson (1977) considered the possibility of forming terrestrial planets as a product of the collision of two massive planets. The original extended protoplanet orbits round off and decay in a resisting medium that forms round the compact star (Woolfson 2003). The mass of the resisting medium, in the form of a disk, exerts a non-central force on the protoplanets so causing their orbits to undergo precession. The orbits have small, but different, inclinations but, because of their precessions at different rates, orbits intersect from time-to-time. Dormand and Woolfson showed that the probability of a planetary collision was small but non-negligible—about 0.1. Support for the plausibility of a planetary collision comes from a NASA Spitzer Space Telescope observation in August 2009, giving evidence of a planetary collision in the vicinity of the young star HD172555 (age 12 My) within the last few thousand years.

The computational facilities and techniques available to Dormand and Woolfson were poor by modern standards and the model they used is now known to be untenable. The idea of a planetary collision is now re-examined using modern computational facilities and techniques and current knowledge.

2 The Model Colliding Planets

Following Dormand and Woolfson, the initial Solar System is taken as having had the existing four major planets plus two others, named for convenience Bellona and Enyo,¹ whose characteristics are given in Table 1. Their internal structures were modelled in four layers, taking into account that segregation by density would be incomplete. The layers were—a core consisting of iron-plus-silicate, a mantle that was mostly silicate but with some iron, a layer of hydrogen-containing molecules plus silicates and, finally, a hydrogen–helium atmosphere.

Table 1 The characteristics of the colliding planets

The ratio of deuterium to hydrogen (D/H) in the universe at large is 2 × 10⁻⁵, which is also the overall ratio in star-forming clouds. However recent work shows that the ratio in molecular species in icy grains in star-forming clouds, and in protostars within them, is much higher. In the cloud L134 N the ratio NHD₂/NH₃ is 0.005 and in the protostar 16293E it is 0.03 (Roueff et al. 2000; Loinard et al. 2001). For formaldehyde the ratio D₂CO/H₂CO has been found to be in the range 0.01–0.4 in a number of low-mass protostars and prestellar cores (Loinard et al. 2002; Bachmann et al. 2003). The deuterated methanol, CH₃OH, in the protostar IRAS 16293-2422 is greater in quantity than that containing just hydrogen (Parise et al. 2002). The reason for this concentration of deuterium is the phenomenon of grain-surface chemistry. A deuterium atom falling on a grain surface will exchange places with a hydrogen atom in a molecule because this lowers its energy and increases its stability. Over a long period, the process concentrates the deuterium in these molecules to the levels observed. The icy material in planets formed from protostar material by the CT process will also have a high D/H ratio.

Using equations of state given by Tillotson (1962), the distributions of density and temperature were determined for Bellona and Enyo. Point mass models for a SPH simulation were formulated, as described by Woolfson (2007), in which the density of SPH points was highest at the centre, the region of greatest interest for this simulation, and decreased with increasing distance from the centre. Figure 1 gives a view of the projected model, with four layers for each of the planets, just before the collision occurred.

Fig. 1

The four-layer structure of the colliding planets

Each planet was represented by 4,921 SPH points that, although few by modern standards, gave adequate resolution for the system while allowing gravitation to be precisely represented by a pairs calculation.

The proportion of silicate was 0.6 in the core and 0.85 in the mantle for both planets. The SPH points were given masses and values of specific internal energy to represent the calculated distribution of density and temperature. The boundaries of the regions for the two planets, and the number of SPH points in each region, are given in Table 2.

Table 2 Boundary distances from the centre (km) and numbers of SPH points (in parentheses) for the four regions

3 Factors in the Simulation

The contact speed of the planets was chosen as 90 km s⁻¹. Their approach speed when they are far apart, V _∞, is given by

$$ V_{\infty }^{2} = V_{C}^{2} - \frac{{2G(M_{B} + M_{E} )}}{{R_{B} + R_{E} }} $$

(1)

where V _C is the initial impact speed, M _B and M _E the masses of Bellona and Enyo, respectively, and R _B and R _E their radii. This gives V _∞ = 42.9 km s⁻¹. With reference to the Sun the planets will be moving on non-parallel paths; the initial approach speed and impact speeds referred to above are with respect to the centre of mass (CoM) of the two planets. In the CoM reference frame they are moving on parallel paths with an offset, shown as d in Fig. 2, which in the simulation was taken as 7 × 10⁴ km.

Fig. 2

The contact velocities, V _B and V _E relative to the centre of mass and the offset, d

In the simulation, the ice regions, with a D/H ratio taken as 0.01, reached temperatures in excess of 2 × 10⁶ K, at which D–D nuclear reactions occur. In a study of isotopic anomalies in meteorites, Holden and Woolfson (1995), using reaction rates given by Fowler et al. (1967, 1975), determined the dependence of the rate at which D–D reactions occurred with density and temperature. When an ice particle reached a temperature of 3 × 10⁶ K, at which D–D reactions occur at an explosive rate, the temperature was immediately raised to 4 × 10⁸ K, somewhat lower than Holden and Woolfson found for a silicate-ice mixture. This simplified the incorporation of the nuclear reactions without biasing the results towards exaggerating the effect of those reactions. The locations in which the nuclear explosion took place spread through the region of D/H enhancement, although some icy material remote from the collision was little affected.

4 Simulation Results

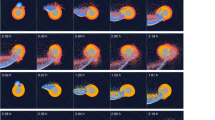
Figure 3 shows projections of the progress of the simulation at nine times. The points representing gas, ice and mantle are dark grey while those representing the core, which is a primary concern of the simulation, are black.

Fig. 3

The progress of the collision. a t = 0, b t = 590 s, c t = 1,326 s, d t = 2,505 s, e t = 3,917 s, f t = 5,336 s, g t = 6,415 s, h t = 7,597 s, i t = 8,609 s

Frame (a) shows the planets just before the collision. In frame (b) the planets are merging but no nuclear reactions have occurred. By frame (c) nuclear reactions have occurred, as is seen by the outwards movement of planetary material. This expansion increases in successive frames but parts of the cores remain compact and steadily move apart.

The simulation used a 4-step Runge–Kutta integration process where tolerance limits were set on the maximum positional, velocity and internal energy difference between integration with a single timestep 2t and with two timesteps each of t. After each 2t integration step the timestep was doubled; if the tolerances were satisfied then the results from two timesteps of t were accepted but, if not, the timestep was repeatedly halved until the tolerances were met. During the whole progress of the integration, timesteps were in the range 4–0.0625 s but mostly 1 or 2 s. In the period before nuclear reactions occurred energy was conserved to 3 parts in 10⁵.

5 The Larger Terrestrial Planets

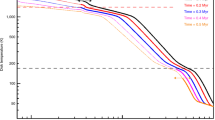
The approach speed of the colliding planets when they were far apart is consistent with a collision in the terrestrial region. It is proposed that the residual cores seen in Fig. 3 formed the planets Earth and Venus, from the Bellona and Enyo residual cores, respectively. The CoM of each core was found and the contained mass for different distances from the CoMs was determined; the results are shown in Fig. 4.

Fig. 4

The variation of the contained mass with distance from the CoM for the residual cores

The Bellona core contains about 2.5 M _⊕ within 20,000 km. The Enyo core was less compact with most of the mass, about 1.5 M _⊕, contained within 100,000 km. Even taking into account the high temperature of the cores, the estimated collapse time for both cores is a few days at most. While the masses of the cores are higher than those of the Earth and Venus, they are similar to those of larger terrestrial-type planets.

6 Orbit Considerations

Perturbation by the Sun would have been negligible during the collision process since it occurred within a small span of 0.005 au. The simulation was carried out with respect to the CoM of the two planets and to find their motions, both before and after the collision with respect to the Sun, requires the position and velocity of the CoM relative to the Sun to be specified. Various position and velocity combinations that were tried led to reasonable outcomes for both pre-and-post-collision orbits. The initial motions of the model planets were in the x–y plane; although in a real situation the orbits would have different small inclinations.

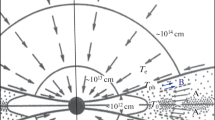
In one orbit calculation the position of the CoM was taken as (−0.376, 0.137) au with velocity components (−2.00, −45.00) km s⁻¹. Table 3, in which V and V’ represent velocity components before and after the collision, gives the parameters of the pre-collision orbits of the planets and post-collision orbits of the residual cores. The results indicate that the pre-collision orbits of Bellona and Enyo had heavily decayed and partially rounded off; the results on orbital evolution given by Woolfson (2003) showed that the rate of orbital evolution increased with the mass of the planet, and these planets were considerably more massive than the present solar-system planets. The initial post-collision core orbits would evolve in the still-present resisting medium to give final radii of rounded orbits somewhere between the initial perihelion and aphelion distances—but where between these values would depend on the radial distribution of the medium. If the medium is far denser at perihelion than at aphelion then the final radius will be close to the perihelion distance. However, in many capture-theory simulations the resisting medium takes on a doughnut form (Fig. 5), in which case the density increases outwards close to the star (Sun in this case) and the final radius will be closer to the original aphelion distance. All that one can say with confidence is that the initial radius of a circular orbit will be somewhere between the original perihelion and aphelion. On that basis, the final orbits shown in Table 3 for the two planets could eventually evolve to those of Venus and Earth.

Table 3 Velocity components before and after the collision with respect to the CoM and with respect to the Sun (primed) and the semi-major axes and eccentricities before and after the collision

Fig. 5

A capture-theory simulation showing a strong doughnut-like captured medium

7 The Moon

Woolfson (2004) described a model for the formation of satellites in a circumplanetary disk based on ideas given by Safronov (1972) for planet formation. Bellona and Enyo, both considerably more massive than Jupiter, would have had extensive families of satellites, some more massive than Ganymede.

The outcomes of the collision for a particular satellite are limited to the following:

• (i) The satellite could be retained by one or other of the planets.

• (ii) The satellite could end up in a heliocentric orbit.

• (iii) The satellite could escape from the Solar System.

• (iv) The satellite could be completely disrupted by debris from the collision.

Trial calculations have shown that the most likely outcomes are (ii) and (iii). The least likely is (iv). Here we explore the possibility that the Moon was a satellite that was left in orbit around the Bellona residual core—now Earth.

A curious feature of the Moon is its hemispherical asymmetry. The nearside is characterized by large maria while the far side is predominantly heavily cratered highlands. Altimeter measurements from a lunar satellite have shown that the far side has large basins formed by huge projectiles but they did not fill with magma from below. To explain this observation it was postulated that the hemispherical asymmetry is due to a difference in crustal thickness on the two hemispheres; large projectiles falling on the nearside penetrated into molten material below the crust to give volcanism, but they could not do so on the far side—except in one case that produced the small Mare Moscoviense. Lunar seismometer measurements have confirmed that, while crustal thickness is variable, the average thickness on the far side is about 20 km greater than that on the nearside.

However, a satellite formed as a plastic body in synchronous orbit around a planet would be expected to have a thicker low-density crust on the nearside. Due to its figure and internal distribution of material, the Moon should have presented the same thicker-crust face to the Earth.

The answer to this conundrum is that the nearside of the Moon would have been heavily abraded by debris from the collision moving at speeds of order 100 km s⁻¹, much greater than the 2.4 km s⁻¹ escape speed from the Moon. Fast projectiles striking the Moon would have shared their energy with surface material, giving much of it sufficient speed to escape; this is the process of abrasion. A projectile from the collision might be expected to abrade a few times its own mass from the surface of the Moon.

A back-of-envelope calculation shows that debris could have removed 50 km or so of surface material from the exposed hemisphere of the Moon. If the Moon, of radius r, were at a distance R from the collision and the debris was isotropically emitted then the mass striking the Moon, M _d , would be

$$ M_{d} = \frac{{r^{2} }}{{4R^{2} }}M_{s} $$

(2)

where M _s is the total mass of solid debris material. Assuming a density of 3,000 kg m⁻³ for lunar crustal material, the total mass of a 50 km thickness from one hemisphere is 2.8 × 10²¹ kg. The ratio of the mass removed from the Moon to that striking the Moon’s surface is then

$$ \alpha = \frac{{2.8 \times 10^{21} }}{{M_{d} }} = \frac{{2.8 \times 10^{21} \times 4R^{2} }}{{r^{2} M_{s} }} $$

(3)

From Table 1 M _s is likely to be of order 20 M _⊕. Taking R = 5 × 10⁵ km, a typical satellite orbital radius, we find α = 8. The arriving debris has a speed more than 40 times the escape speed (energy more than 1,600 times the escape energy) and this value of α is quite plausible.

8 The Smaller Terrestrial Planets

Here we propose that Mercury and Mars, with twice and four times the mass of Ganymede respectively, were two large satellites released into independent heliocentric orbits. The question is whether features of those bodies can be related to the collision scenario.

8.1 Mars

Like the Moon, Mars has hemispherical asymmetry with a 3 km-high scarp separating magma-covered lightly-cratered northern plains and southern heavily-cratered highlands containing one large and deep depression, the Hellas Basin, produced by an exceptionally energetic projectile. Early Mars would have had magma close to its surface; heavy abrasion of one face would have removed the greater part of the crust and volcanism would have produced a magma plain, as is observed.

The Moon’s spin axis is in the plane that separates the two hemispheres. Tidal coupling to the Earth gave synchronous rotation with the same face towards Earth as was towards the original parent planet. However, for Mars, not linked to another body, the dividing plane is inclined at 55° to the spin axis.

For Mars the crust could easily have moved over a molten mantle—something akin to continental drift. A theorem by Lamy and Burns (1972) states that a spinning body with internal energy dissipation eventually settles down with its spin axis along the principal axis of maximum moment of inertia—achieved by a process known as polar wander. With the southern highlands as a reference level, McConnell and Woolfson (1983) modelled surface features of Mars either as positive features—such as the Tharsis uplift, Argyre plain, Elysium plain and Olympus Mons—or as negative features such as the northern plains and the Hellas Basin. They found that the principal axis of maximum moment of inertia was 11.9° from the spin axis; the probability of being this close or closer just by chance is about 0.02.

8.2 Mercury

The high density of Mercury is due to the large size of its iron core—similar to that of Mars—relative to its mantle. It has often been suggested that Mercury was originally similar to Mars but that some colliding body stripped away part of its mantle. If Mercury were a close satellite, or in the plane of the collision interface where the debris density was high (see Fig. 3), then most of its mantle that faced the collision could have been removed. Self-gravitational forces would then have restored the spherical form of Mercury to give a body of high density. Subsequent events—cooling, shrinkage, volcanism and bombardment—would then have given the present surface features.

9 Asteroids and Comets: Initial Formation

The idea that asteroids came from a disrupted planet was considered by Napier and Dodd (1973) who concluded that the idea was untenable since no conceivable source of energy was available to break up and disperse the material of a planet. The preferred theory of origin is that they come from the collisions of satellite-size parent bodies formed from collections of planetesimals that were left over after planets were assembled within a nebula.

There are two main ideas about the origin of comets. The comets of the Oort Cloud (Oort 1948) are interpreted as either weakly bound captured objects or residual planetesimals produced at large distances from the Sun where volatile materials would remain solid.

A planetary-collision postulate reactivates the idea that asteroids are fragments of planets and at the same time gives a source of comets. Core, mantle and ice fragments are thrown out in all directions. Whether debris is retained or lost from the system, depends on its intrinsic energy, which has been analysed separately for the three kinds of material, with only SPH points outside the spheres of influence of the two cores included in the analysis. The results, displayed in Fig. 6, give the mass in Earth units per unit intrinsic internal enrgy, expressed in GJ/kg.

Fig. 6

The distribution of dispersed material from the collision. The graphs show the distribution of mass in Earth units per unit intrinsic energy (GJ/kg)

More than one-half of core material is retained and a somewhat smaller fraction of mantle material. By contrast the majority of the ice is expelled from the system. There are gradual transitions in iron-silicate and silicate-ice structure and the retained mantle material furthest out would tend to contain more volatile content and be identified as C-type asteroids with compositions similar to that of carbonaceous chondrites. Observations indicate that C-type asteroids tend to be further from the Sun than S-and-M-type asteroids, which is consistent with the model suggested here.

The eccentricities and inclinations of the retained material are shown in Fig. 7. There is a tendency for inclination to increase with eccentricity. Nearly all the core and mantle orbits are prograde but a considerable proportion of the ice orbits are retrograde. Ice debris has a much higher speed than the mantle and core debris because when it is first produced it has less external solid material to constrain its motion. In an extreme case, where the average speed of the ice debris with respect to the CoM is much greater than the speed of the CoM in its orbit about the Sun, the resultant motion of the debris will give almost as much of it in retrograde orbits as in direct orbits. Alternatively, if the average speed of the mantle and core debris is very small compared to that of the CoM relative to the Sun then the resultant debris velocity puts virtually all of it into direct orbits.

Fig. 7

The eccentricities and inclinations of the retained material

Most core and mantle material would either have been expelled from the Solar System or been absorbed by major planets. The estimated total mass of asteroids, about 4 % of that of the Moon, is the tiny fraction that ended up in safe orbits.

10 Comets—Post-Formation Interactions

When asteroids and comets formed, the existing major planets were on extended, but evolving orbits. Once they settled into their present orbits the majority of the debris with orbits entering the planetary region would have had little likelihood of long-term survival.

Some debris went further out and could undergo other kinds of interaction. The four existing major planets spent most time in the outer parts of their orbits near aphelion. Figure 8 shows an interaction between a comet, with original aphelion 110 au and perihelion 0.5 au, with a planet of Jupiter mass in an orbit with aphelion 100 au and perihelion 10 au. In the original orbit the comet could not have survived but after the interaction with the closest approach to the planet 1.84 × 10⁶ km the orbit changes to one with semi-major axis 75.88 au and perihelion, 42.11 au, well within the Kuiper Belt.

Fig. 8

Debris interacting with a planet in an evolving orbit is perturbed into an orbit with a small perihelion to a much larger one

For this process it is necessary for the bodies to approach each other closely, which requires them to be not too far from coplanar. For this reason, given the results in Fig. 7, it is unlikely that much debris was moved into safe orbits in this way.

Another mechanism involves the effect of the medium on newly formed cometary bodies. For bodies the size and density of comets, the main resistance is due to the ram pressure they experience from the impact of the medium. For a spherical comet of radius a the force experienced will be

$$ {\mathbf{F}} = \pi \rho a^{2} V{\mathbf{V}} $$

(4)

where ρ is the local density of the medium and V the velocity of the medium relative to the comet. Figure 9 gives the variation of perihelion for a comet of mass 7 × 10¹² kg, of density 500 kg m⁻³ (estimates vary between 100 and 1,000 kg m⁻³) with original perihelion 0.5 au and various original aphelia. The medium had a total mass of 40 M _J with a distribution of density similar to that seen in Fig. 5. All orbits with original semi-major axes greater than about 60 au ended up with perihelia within the Kuiper-belt region. Their aphelia stretch out to thousands, of au and represent the inner cloud of comets postulated by Bailey (1983). The present model would suggest a continuous distribution of comets from the Kuiper belt to the Oort Cloud. While comets are observed coming from the inner Kuiper Belt region, perturbed by Neptune, and from the Oort Cloud, perturbed by external bodies, there are no significant perturbing bodies in the centre part of the distribution, so its presence is not detected.

Fig. 9

The changes of the perihelion with time for comets with original perihelia 0.5 au and various initial semi-major axes, a ₀

This process for increasing the perihelion described here is not very effective for core and mantle fragments because of their much higher density.

11 Dwarf Planets

The five dwarf planets—Ceres, Pluto, Eris, Makemake and Haumea all have typical satellite masses and, with the exception of Pluto (Woolfson 1999), we identify them as satellites of the colliding planets that were diverted into the Kuiper Belt. During the period of orbital rounding-off by the process described by Woolfson (2003), the annular form of the resisting medium, as seen in Fig. 5, would increase the perihelion of their orbits. Once the orbits became circular their orbital evolution would be by the Type I migration process (Goldreich and Tremaine 1979). Any satellites ending with its perihelion within the Kuiper Belt would survive while others would eventually be swept up by a major planet. The exception is Ceres that was left in a safe orbit within the asteroid belt. Since released satellites would tend to have small inclinations the process for orbital evolution illustrated in Fig. 8 might also have been effective.

Other satellites, some possibly more massive than the existing dwarf planets, could have left the Solar System, been absorbed by major planets or could be undiscovered in outer regions of the Kuiper Belt. Another possibility is that one or more of them may have reached the Oort Cloud. It has been suggested that the tendency for some new comets to come from similar directions with similar orbital parameters may be due to the presence of major perturbing bodies within the Oort Cloud.

12 Summary and Comments

It has been shown that a collision of two major planets could give surviving cores similar in type to terrestrial planets. Different outcomes, but with the same general characteristics, were found for collision simulations with mass combinations, in Earth units, (452, 169), (618, 116) and (990, 333).

An event as cataclysmic as a planetary collision would leave its signature all over the Solar System and to discuss it adequately requires a holistic approach involving many solar-system features; detailed treatments of some individual features will follow later. In one sense the collision hypothesis can be regarded as ‘efficient’. All the components of the post-collision system—surviving cores, satellites, debris of various types and the isotopes produced in the nuclear explosion—appear as important features of the Solar System today—the larger terrestrial planets, the presence and characteristics of the Moon, Mars and Mercury, asteroids, comets in the Kuiper Belt and the Oort Cloud, dwarf planets, the relationship between Neptune, Pluto and Triton (Woolfson 1999) and isotopic anomalies in meteorites (Holden and Woolfson 1995; Woolfson 2011).

The CT, which provides the scenario for the collision event, is based on observations—e.g. the existence of the dense embedded state of an evolving cluster and non-controversial theory and simulation of tidal interactions and the instability in gaseous filaments. Another important component of the collision postulate is the existence of deuterium-rich grains, for which there is observational evidence, which become incorporated into protoplanets. This provides the means of triggering a nuclear-reaction chain that gives both the energy for dispersing the planets and the isotopes that explain observed light-atom isotopic anomalies in meteorites.

The presently available alternative to the planetary-collision hypothesis is a large number of ad hoc explanations for individual features. For example, the single explanation for many isotopic anomalies replaces a number of ad hoc explanations for individual anomalies, some involving the transport through space of grains from distant stars. Another example is the well-supported collision hypothesis for Moon formation (Benz et al. 1986) that convincingly models the existence of the Moon as an Earth satellite—but nothing else.

A final comment—if the planetary-collision postulate were accepted, and dwarf planets were redefined as ex-satellites of the colliding planets, then there would be six, the five defined by the present criteria less Pluto, plus Mars and Mercury.