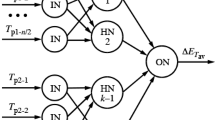
The effect of covariances between the resistances of a standard platinum resistance thermometer when measuring temperature and its resistances at fixed points in a calibration on the uncertainty of temperature measurement is shown. A procedure for calculating the uncertainties, which enables any covariances that occur to be taken into account, is considered.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
S. Duris, R. Palencar, and J. Ranostaj, “The effect of covariance on uncertainty when constructing the ITS-90 temperature scale,” Izmer. Tekhn., No. 4, 44–49 (2008); Measur. Techn., 51, No. 4, 412–420 (2008).
Guide to the Expression of Uncertainty in Measurement, ISO, Geneva (1993).
R. Palencar, S. Duris, and J. Ranostaj, “Algebraic approach for calculating the total uncertainties in SPRT measurement,” TEMPMEKO & ISHM 2010: Abstracts, IMEKO, Portoroz, Slovenia (2010).
S. Duris and R. Palencar, “The influences of covariances on the uncertainty of temperature measurement by resistance thermometer,” Measur. Sci. Rev., 5, No. 1, 15–18 (2005).
S. Duris, R. Palencar, and R. Ranostaj, “Contribution of the SPRT calibration to uncertainty of temperature T90 measured by the calibrated SPRT,” Measur. Sci. Rev., 8, No. 1, 5–10 (2008).
Uncertainties in the Realization of the SPRT Subranges of the ITS-90, BIPM, Sevres (2009).
D. R. White and P. Saunders, “The propagation of uncertainty on interpolated scales, with examples from thermometry,” Metrologia, 37, 285–293 (2000).
D. R. White, “The propagation of uncertainty with non-Lagrangian interpolation,” Metrologia, 38, 63–69 (2001).
D. R. White and P. Saunders, “The propagation of uncertainty with calibration equations,” Measur. Sci. Tech., 18, 2157–2169 (2007).
D. R. White and G. F. Strouse, “Observations on subrange inconsistency in the SPRT interpolations of ITS-90,” Metrologia, 46, 101–108 (2009).
H. Preston-Thomas, “The international temperature scale of 1990,” Metrologia, 27, 3–10 (1990).
W. Bich, “Simple formula for the propagation of variances and covariances,” Metrologia, 33, 181–183 (1996).
C. W. Mayer and D. C. Ripple, “Determination of the uncertainties for ITS-90 realization by SPRTs between fixed points,” Metrologia, 43, 327–340 (2001).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Izmeritel’naya Tekhnika, No. 8, pp. 40–45, August, 2011.
Rights and permissions
About this article
Cite this article
Palencar, R., Duris, S. & Ranostaj, J. Conclusions and some comments on the calculation of uncertainty when constructing a temperature scale. Meas Tech 54, 910–920 (2011). https://doi.org/10.1007/s11018-011-9826-5
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11018-011-9826-5