Steric effects on electroosmotic flow in soft nanochannels

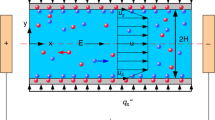
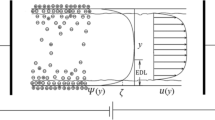
Abstract

A numerical solution is derived of the mixed pressure and electroosmotically driven flow in a soft nanochannel considering the steric effect within electric double layer. The electric potential and the velocity distributions are described by the modified Poisson–Boltzmann equation and the modified Navier–Stokes equation under the conditions of boundary slip and constant charge density on the walls. By  using the finite difference method, the numerical solutions of the electric potential, velocity and the volumetric flow rate are obtained. Results show that the electric potential increases with the steric parameter. The velocity decreases with the steric parameter for lower surface charge density, while opposite trend can be found for higher surface charge density. We compare the results of soft and rigid nanochannels and find the velocity in the soft nanochannel is larger than that in the rigid one except for the case of higher surface charge density.

Appendix

1.1 Numerical algorithm

Differential equations Eqs. (3) and (8) are solved by the numerical model, in conjunction with boundary conditions (4) and (9) in the previous section. These equations are solved using the finite different method. The domain y we considered is in the interval [−1, 0] because of the symmetry about the y axis. The y _i (1 ≤ i≤n) is regarded as the discrete grid points, the step size is h = 1/n, the electric potential ψ at the point y _i is denoted as ψ _i  = ψ _i (y _i ). Equation (3) can be discretized as [39]:

$$\frac{{\psi_{i + 1} - 2\psi_{i} + \psi_{i - 1} }}{{h^{2} }} = \frac{1}{{\lambda^{2} }}\frac{{\sinh (\psi_{i} )}}{{1 + 2v(\cosh (\psi_{i} ) - 1)}},\;i = N + 1, \ldots ,n - 1,$$

(11a)

$$\frac{{\psi_{i + 1} - 2\psi_{i} + \psi_{i - 1} }}{{h^{2} }} = \frac{1}{{\lambda^{2} }}\frac{{\sinh (\psi_{i} )}}{{1 + 2v(\cosh (\psi_{i} ) - 1)}} - \frac{1}{{\lambda_{FCL}^{2} }},\;i = \, 2, \ldots ,\,N - 1,$$

(11b)

where N means the grid point at the interface between soft layer and electrolyte solution. The corresponding boundary conditions (Eq. 4) are discretized as:

$$\frac{{\psi_{n} - \psi_{n - 1} }}{h} = 0\;{\text{and}}\;\frac{{\psi_{n + 1} - \psi_{n} }}{h} = 0,\;\;i = n,$$

(12a)

$$\psi_{N} = \psi_{N} ,\;\;i = N,$$

(12b)

$$\frac{{\psi_{N + 1} - \psi_{N} }}{h} = \frac{{\psi_{N} - \psi_{N - 1} }}{h},\;\;i = N,$$

(12c)

$$\frac{{\psi_{2} - \psi_{1} }}{h} = - \varOmega \;{\text{and}}\;\frac{{\psi_{1} - \psi_{0} }}{h} = - \varOmega ,\;\;i = 1.$$

(12d)

In order to improve accuracy of the first order derivative boundary conditions, imaginary electrical potentials ψ ₀ and ψ _n+1 are introduced in Eqs. (12a) and (12d), which can be expressed by using the values of internal points near the wall. Substituting Eq. (12d) into Eq. (11b) and Eq. (12a) into Eq. (11a), we have

$$\frac{{2\psi_{2} - 2\psi_{1} + 2h\varOmega }}{{h^{2} }} = \frac{1}{{\lambda^{2} }}\frac{{\sinh (\psi_{1} )}}{{1 + 2v(\cosh (\psi_{1} ) - 1)}} - \frac{1}{{\lambda_{FCL}^{2} }},\;i = 1,$$

(13a)

$$\frac{{2\psi_{n - 1} - 2\psi_{n} }}{{h^{2} }} = \frac{1}{{\lambda^{2} }}\frac{{\sinh (\psi_{n} )}}{{1 + 2v(\cosh (\psi_{n} ) - 1)}},\;i = n.$$

(13b)

It is noted that the Eqs. (13a) and (13b) are taken as the first (i = 1) and the last (i = n) discrete equations. At the node y _N , the electrical potential satisfies the Eqs. (12b, c). Solving these discretized nonlinear differential equation groups by using multivariate Newton’s iteration method. The function F(ψ) is provided by

$$F\left( \psi \right) = \left[ \begin{array}{l} f_{1} (\psi_{1} ,\psi_{2} , \cdots \psi_{n} ) \hfill \\ f_{2} (\psi_{1} ,\psi_{2} , \cdots \psi_{n} ) \hfill \\ \vdots \hfill \\ f_{N} (\psi_{1} ,\psi_{2} , \cdots \psi_{n} ) \hfill \\ \vdots \hfill \\ f_{{n{ - }1}} (\psi_{1} ,\psi_{2} , \cdots \psi_{n} ) \hfill \\ f_{n} (\psi_{1} ,\psi_{2} , \cdots \psi_{n} ) \hfill \\ \end{array} \right] = \left[ \begin{array}{l} \frac{{2\psi_{2} - 2\psi_{1} + 2h\varOmega }}{{h^{2} }} - \frac{1}{{\lambda^{2} }}\frac{{\sinh (\psi_{1} )}}{{1 + 2v(\cosh (\psi_{1} ) - 1)}} - \frac{1}{{\lambda_{FCL}^{2} }} \hfill \\ \frac{{\psi_{3} - 2\psi_{2} + \psi_{1} }}{{h^{2} }} - \frac{1}{{\lambda^{2} }}\frac{{\sinh (\psi_{2} )}}{{1 + 2v(\cosh (\psi_{2} ) - 1)}} - \frac{1}{{\lambda_{FCL}^{2} }} \hfill \\ \vdots \hfill \\ \frac{{\psi_{N + 1} - \psi_{N} }}{h} - \frac{{\psi_{N} - \psi_{N - 1} }}{h} \hfill \\ \vdots \hfill \\ \frac{{\psi_{n} - 2\psi_{n - 1} + \psi_{n - 2} }}{{h^{2} }} - \frac{1}{{\lambda^{2} }}\frac{{\sinh (\psi_{n - 1} )}}{{1 + 2v(\cosh (\psi_{n - 1} ) - 1)}} \hfill \\ \frac{{2\psi_{n - 1} - 2\psi_{n} }}{{h^{2} }} - \frac{1}{{\lambda^{2} }}\frac{{\sinh (\psi_{n} )}}{{1 + 2v(\cosh (\psi_{n} ) - 1)}} \hfill \\ \end{array} \right]$$

(14)

The Jacobian DF(ψ) of F(ψ) can be written as

where $A = - 2 - \frac{{h^{2} }}{{\lambda^{2} }}\frac{{\left[ {\cosh (\psi_{i} )(1 - 2v) + 2v(\cosh^{2} (\psi_{i} ) - \sinh^{2} (\psi_{i} ))} \right]}}{{(1 - 2v + 2v\cosh (\psi_{i} ))^{2} }}$. The ith equation of the partial derivative, the ith component of F(ψ), obtained the Jacobian’s ith row with respect to each ψ _j , and we utilize the Newton’s Method to solve the problem of the boundary value discretized version since its means to solve F(ψ) = 0. The ψ ^k+1=ψ ^k − [DF(ψ ^k)]⁻¹ F(ψ ^k) is iterated by Newton’s Method, where k is iteration number. In this paper, we take k = 20. Usually, to best perform the iteration, we solve Δψ = ψ ^k+1−ψ ^k in the equation DF(ψ ^k)Δψ = −F(ψ ^k). The numerical solution is obtained in the next section.