Skip to main content
SpringerLink
Log in

Weakly nonlinear dynamics of taut strings traveled by a single moving force

  • New Trends in Dynamics and Stability
  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

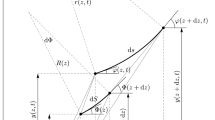
The dynamical response of a taut string traveled by a single moving force is here studied in the nonlinear regime. The equations of motion of the system, accounting for geometric nonlinearities and external damping, are discussed and then studied through perturbation and numerical methods. In particular, the Multiple Scale Method and the Straightforward Expansion are successfully applied to obtain semi-analytical results, and direct numerical integrations are performed on the equations of motion discretized via a Galerkin approach; a solution through the finite-difference method is also developed. Particular attention is devoted to the dynamic increment of tension, which is the main nonlinear effect induced by the traveling force. Using values of model parameters deducted from the literature, the agreement of semi-analytical results with numerical ones is discussed, showing the good behavior of the Straightforward Expansion and pointing out the importance of the geometric nonlinearity for certain combinations of the parameters involved.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Rusin J, Sniady P, Sniady P (2011) Vibration of double-string complex system under moving forces. Closed solutions. J Sound Vib 330:404–415

    Article  ADS  Google Scholar 

  2. Piccardo G, Tubino F (2012) Dynamic response of Euler–Bernoulli beams to resonant harmonic moving loads. Struct Eng Mech 44(5):681–704

    Article  Google Scholar 

  3. Bajer C, Dyniewicz B (2012) Numerical analysis of vibrations of structures under moving inertial loads. Springer-Verlag, Berlin. iSBN: 978-3-642-29547-8

  4. Bersani A, Della Corte A, Piccardo G, Rizzi N (2016) An explicit solution for the dynamics of a taut string of finite length carrying a traveling mass: the subsonic case. Z Angew Math Phys 67(108):1–17

    MathSciNet  MATH  Google Scholar 

  5. Yang B, Tan C, Bergman L (1998) On the problem of a distributed parameter system carrying a moving oscillator. In: Tzou H, Bergman L (eds) Dynamics and control of distributed systems. Cambridge University Press, New York, pp. 69–94. iSBN:0-521-55074-2

  6. Caprani C, Ahmadi E (2016) Formulation of human–structure interaction system models for vertical vibration. J Sound Vib 377:346–367

    Article  ADS  Google Scholar 

  7. Cazzani A, Wagner N, Ruge P, Stochino F (2016) Continuous transition between traveling mass and traveling oscillator using mixed variables. Int J Non-Linear Mech 80:82–95

    Article  Google Scholar 

  8. Ferretti M, Piccardo G (2013) Dynamic modeling of taut strings carrying a traveling mass. Contin Mech Thermodyn 25(2–4):469–488

    Article  ADS  MathSciNet  MATH  Google Scholar 

  9. Fryba L (1999) Vibrations of Solids and Structures under Moving Loads. Thomas Telford, London. iSBN: 978-0-7277-3539-3

  10. Ouyang H (2011) Moving-load dynamic problems: a tutorial (with a brief overview). Mech Syst Signal Process 25:2039–2060

    Article  ADS  Google Scholar 

  11. Chang T-P, Liu Y-N (1996) Dynamic finite element analysis of a nonlinear beam subjected to a moving load. Int J Solids Struct 33(12):1673–1688

    Article  MATH  Google Scholar 

  12. Mamandi A, Kargarnovin M, Younesian D (2010) Nonlinear dynamics of an inclined beam subjected to a moving load. Nonlinear Dyn 60:277–293

    Article  MATH  Google Scholar 

  13. Wu J, Chen C (1989) The dynamic analysis of a suspended cable due to a moving load. Int J Numer Methods Eng 28:2361–2381

    Article  MATH  Google Scholar 

  14. Wang L, Rega G (2010) Modelling and transient planar dynamics of suspended cables with moving mass. Int J Solids Struct 47:2733–2744

    Article  MATH  Google Scholar 

  15. Pesterev A, Bergman L (2000) An improved series expansion of the solution to the moving oscillator problem. J Vib Acoust ASME 122:54–61

    Article  Google Scholar 

  16. Gavrilov S (2002) Nonlinear investigation of the possibility to exceed the critical speed by a load on a string. Acta Mech 154:47–60

    Article  MATH  Google Scholar 

  17. Gavrilov S, Eremeyev V, Piccardo G, Luongo A (2016) A revisitation of the paradox of discontinuous trajectory for a mass particle moving on a taut string. Nonlinear Dyn 86(4):2245–2260

    Article  MathSciNet  MATH  Google Scholar 

  18. Metrikine A (2004) Steady state response of an infinite string on a non-linear visco-elastic foundation to moving point loads. J Sound Vib 272:1033–1046

    Article  ADS  Google Scholar 

  19. Liu I-S, Rincon M (2003) Effect of moving boundaries on the vibrating elastic string. Appl Numer Math 47:159–172

    Article  MathSciNet  MATH  Google Scholar 

  20. Kang Y, Lee M, Jung I (2009) Stabilization of the Kirchhoff type wave equation with locally distributed damping. Appl Math Lett 22:719–722

    Article  MathSciNet  MATH  Google Scholar 

  21. Nayfeh A, Mook D (1979) Nonlinear oscillations. Wiley, New York

    MATH  Google Scholar 

  22. Luongo A, Zulli D (2013) Mathematical models of beams and cables. ISTE Wiley, London, U.K.

    Book  Google Scholar 

  23. Wickert J (1992) Non-linear vibration of a traveling tensioned beam. Int J Non-Linear Mech 27(3):503–517

    Article  MATH  Google Scholar 

  24. Luongo A, Piccardo G (1998) Non-linear galloping of sagged cables in 1:2 internal resonance. J Sound Vib 214(5):915–940

    Article  ADS  Google Scholar 

  25. Nayfeh A (1993) Introduction to perturbation techniques. Wiley, New York

    MATH  Google Scholar 

  26. Luongo A, Piccardo G (2016) Dynamics of taut strings traveled by train of forces. Contin Mech Thermodyn 28(1–2):603–616

    Article  ADS  MathSciNet  MATH  Google Scholar 

  27. Chen L-Q, Ding H (2008) Two nonlinear models of a transversely vibrating string. Arch Appl Mech 78:321–328

    Article  Google Scholar 

  28. Eftekhari S (2015) A differential quadrature procedure with regularization of the Dirac-delta function for numerical solution of moving load problem. Lat Am J Solids Struct 12(7):1241–1265

    Article  Google Scholar 

  29. Eftekhari S (2016) A differential quadrature procedure for linear and nonlinear steady state vibrations of infinite beams traversed by a moving point load. Meccanica 51(10):2417–2434

    Article  MathSciNet  MATH  Google Scholar 

  30. Greco L, Cuomo M (2015) Consistent tangent operator for an exact Kirchhoff rod model. Contin Mech Thermodyn 25(4–5):861–877

    Article  ADS  MathSciNet  MATH  Google Scholar 

  31. Cazzani A, Cattani M, Mauro R, Stochino F (2017) A simplified model for railway catenary wire dynamics. Eur J Environ Civil Eng 21(7–8):936–959

    Article  Google Scholar 

  32. Pagnini L, Repetto M (2012) The role of parameter uncertainties in the damage prediction of the alogwind-induced fatigue. J Wind Eng Ind Aerodyn 104–106:227–238

    Article  Google Scholar 

  33. Roveri N, Carcaterra A (2012) Damage detection in structures under traveling loads by Hilbert–Huang transform. Mech Syst Signal Process 28:128–144

    Article  ADS  Google Scholar 

  34. Porfiri M, dell’Isola F, Mascioli F Frattale (2004) Circuit analog of a beam and its application to multimodal vibration damping, using piezoelectric transducers. Int J Circuit Theory Appl 32(4):167–198

    Article  MATH  Google Scholar 

  35. Giorgio I, Galantucci L, Della Corte A, Del Vescovo D (2015) Piezo-electromechanical smart materials with distributed arrays of piezoelectric transducers: current and upcoming applications. Int J Appl Electromagn Mech 47(4):1051–1084

    Article  Google Scholar 

  36. D’Annibale F, Rosi G, Luongo A (2016) Piezoelectric control of Hopf bifurcations: a non-linear discrete case study. Int J Non-Linear Mech 80:160–169

    Article  Google Scholar 

  37. Pagnini L, Piccardo G (2016) The three-hinged arch as an example of piezomechanic passive controlled structure. Contin Mech Thermodyn 28(5):1247–1262

    Article  ADS  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. DICEAA and M&MoCS, University of L’Aquila, L’Aquila, Italy

    Manuel Ferretti & Angelo Luongo

  2. DICCA, Polytechnic School, University of Genoa (Italy), Genoa, Italy

    Giuseppe Piccardo

Authors
  1. Manuel Ferretti
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Giuseppe Piccardo
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Angelo Luongo
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Giuseppe Piccardo.

Ethics declarations

conflict of interest

The authors declare that they have no conflict of interest.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ferretti, M., Piccardo, G. & Luongo, A. Weakly nonlinear dynamics of taut strings traveled by a single moving force. Meccanica 52, 3087–3099 (2017). https://doi.org/10.1007/s11012-017-0690-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-017-0690-5

Keywords

Search

Navigation