Skip to main content
SpringerLink
Log in

Non-linear viscoelastic behavior of polymer melts interpreted by fractional viscoelastic model

  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

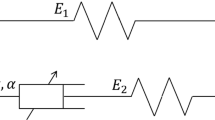
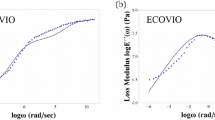
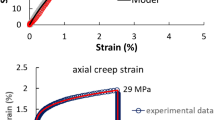
Very recently, researchers dealing with constitutive law pertinent viscoelastic materials put forward the successful idea to introduce viscoelastic laws embedded with fractional calculus, relating the stress function to a real order derivative of the strain function. The latter consideration leads to represent both, relaxation and creep functions, through a power law function. In literature there are many papers in which the best fitting of the peculiar viscoelastic functions using a fractional model is performed. However there are not present studies about best fitting of relaxation function and/or creep function of materials that exhibit a non-linear viscoelastic behavior, as polymer melts, using a fractional model. In this paper the authors propose an advanced model for capturing the non-linear trend of the shear viscosity of polymer melts as function of the shear rate. Results obtained with the fractional model are compared with those obtained using a classical model which involves classical Maxwell elements. The comparison between experimental data and the theoretical model shows a good agreement, emphasizing that fractional model is proper for studying viscoelasticity, even if the material exhibits a non-linear behavior.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Flügge W (1967) Viscoelasticity. Blaisdell Publishing Company, Waltham

    MATH  Google Scholar 

  2. Pipkin A (1972) Lectures on viscoelasticity theory. Springer, New York

    Book  MATH  Google Scholar 

  3. Christensen RM (1982) Theory of viscoelasticity: an introduction. Academic Press, New York

    Google Scholar 

  4. Ferry JD (1970) Viscoelastic properties of polymers. Wiley, New York

    Google Scholar 

  5. Schmidt A, Gaul L (2002) Finite element formulation of viscoelastic constitutive equations using fractional time derivatives. Nonlinear Dyn 29:37–55

    Article  MATH  Google Scholar 

  6. Di Paola M, Failla G, Pirrotta A (2012) Stationary and non-stationary stochastic response of linear fractional viscoelastic systems. Probab Eng Mech 28:85–90

    Article  Google Scholar 

  7. Di Paola M, Heuer R, Pirrotta A (2013) Fractional visco-elastic Euler–Bernoulli beam. Int J Solids Struct 50:3505–3510

    Article  Google Scholar 

  8. Di Lorenzo S, Di Paola M, Pinnola FP, Pirrotta A (2014) Stochastic response of fractionally damped beams. Probab Eng Mech 35:37–43

    Article  Google Scholar 

  9. Alotta G, Di Paola M, Pirrotta A (2014) Fractional Tajimi–Kanai model for simulating earthquake ground motion. Bull Earthq Eng (BEEE) 12:2495–2506

    Article  Google Scholar 

  10. Pirrotta A, Cutrona S, Di Lorenzo S (2015) Fractional visco-elastic Timoshenko beam from elastic Euler–Bernoulli beam. Acta Mech 226:179–189

    Article  MathSciNet  MATH  Google Scholar 

  11. Pirrotta A, Cutrona S, Di Lorenzo S, Di Matteo A (2015) Fractional visco-elastic Timoshenko beam deflection via single equation. Int J Numer Meth Eng 104:869–886

    Article  MathSciNet  MATH  Google Scholar 

  12. Bucher C, Pirrotta A (2015) Dynamic finite element analysis of fractionally damped, structural systems in the time domain. Acta Mech 226:3977–3990

    Article  MathSciNet  MATH  Google Scholar 

  13. Gonsovski VL, Rossikhin YA (1973) Stress waves in a viscoelastic medium with a singular hereditary kernel. J Appl Mech Tech Phys 14:595–597

    Article  ADS  Google Scholar 

  14. Schiessel H, Blumen A (1993) Hierarchical analogues to fractional relaxation equations. J Phys A 26:5057–5069

    Article  ADS  Google Scholar 

  15. Stiassnie M (1973) On the application of fractional calculus on the formulation of viscoelastic models. Appl Math Model 3:300–302

    Article  MATH  Google Scholar 

  16. Bagley RL, Torvik PJ (1979) A generalized derivative model for an elastomer damper. Shock Vib Bull 49:135–143

    Google Scholar 

  17. Bagley RL, Torvik PJ (1983) A theoretical basis for the application of fractional calculus. J Rheol 27:201–210

    Article  ADS  MATH  Google Scholar 

  18. Bagley RL, Torvik PJ (1983) Fractional calculus: a different approach to the analysis of viscoelastically damped structures. Am Inst Aeronaut Astronaut (AIAA) J 20:741–774

    Article  MATH  Google Scholar 

  19. Bagley RL, Torvik PJ (1986) On the fractional calculus model of viscoelastic behavior. J Rheol 30:133–155

    Article  ADS  MATH  Google Scholar 

  20. Hilfer R (2000) Applications of fractional calculus in physics. World Scientific, Singapore

    Book  MATH  Google Scholar 

  21. Mainardi F, Gorenflo R (2007) Time-fractional derivatives in relaxation processes: a tutorial survey. Fract Calc Appl Anal 10:269–308

    MathSciNet  MATH  Google Scholar 

  22. Evangelatos GI, Spanos PD (2011) An accelerated newmark scheme for integrating the equation of motion of nonlinear systems comprising restoring elements governed by fractional derivatives. Recent Adv Mech 1:159–177

    Article  Google Scholar 

  23. Failla G, Pirrotta A (2012) On the stochastic response of a fractionally-damped duffing oscillator. Commun Nonlinear Sci Numer Simul 17:5131–5142

    Article  ADS  MathSciNet  MATH  Google Scholar 

  24. Di Matteo A, Lo Iacono F, Navarra G, Pirrotta A (2015) Innovative modeling of tuned liquid column damper motion. Commun Nonlinear Sci Numer Simul 23:229–244

    Article  ADS  Google Scholar 

  25. Cao L, Pu H, Li Y, Li M (2016) Time domain analysis of the weighted distributed order rheological model. Mech Time-Depend Mater. doi:10.1007/s11043-016-9314-z

    Google Scholar 

  26. Samko SG, Kilbas AA, Marichev OI (1993) Fractional integrals and derivatives. Gordon and Breach Science, Amsterdam

    MATH  Google Scholar 

  27. Podlubny I (1999) Fractional differential equations. Academic Press, New York

    MATH  Google Scholar 

  28. Nutting PG (1921) A new general law deformation. J Franklin Inst 191:678–685

    Article  Google Scholar 

  29. Gemant A (1936) A method of analyzing experimental results obtained by elasto-viscous bodies. Physics 7:311–317

    Article  ADS  Google Scholar 

  30. Di Paola M, Pirrotta A, Valenza A (2011) Visco-elastic behavior through fractional calculus: an easier method for best fitting experimental results. Mech Mater 43:799–806

    Article  Google Scholar 

  31. Celauro C, Fecarotti C, Pirrotta A, Collop AC (2012) Experimental validation of a fractional model for creep/recovery testing of asphalt mixtures. Constr Build Mater 36:458–466

    Article  Google Scholar 

  32. Fecarotti C, Celauro C, Pirrotta A (2012) Linear VISCOELAstic (LVE) behaviour of pure bitumen via fractional model. Procedia Soc Behav Sci 53:450–461

    Article  Google Scholar 

  33. Di Paola M, Fiore V, Pinnola FP, Valenza A (2014) On the influence of the initial ramp for a correct definition of the parameters of fractional viscoelastic materials. Mech Mater 69:63–70

    Article  Google Scholar 

  34. Cataldo E, Di Lorenzo S, Fiore V, Maurici M, Nicoletti F, Pirrotta A, Scaffaro R, Valenza A (2015) Bending test for capturing the vivid behavior of giant reeds, returned through a proper fractional visco-elastic model. Mech Mater 89:159–168

    Article  Google Scholar 

  35. Celauro C, Fecarotti C, Pirrotta A (2015) An extension of the fractional model for construction of asphalt binder master curve. Eur J Environ Civil Eng. doi:10.1080/19648189.2015.1095685

    Google Scholar 

  36. Welch SWJ, Rorrer RAL, Duren RG (1999) Application of time-based fractional calculus methods to viscoelastic creep and stress relaxation of materials. Mech Time-Depend Mater 3:279–303

    Article  ADS  Google Scholar 

  37. Eldred LB, Baker WP, Palazotto AN (1996) Numerical application of fractional derivative model constitutive relations for viscoelastic materials. Comput Struct 60:875–882

    Article  MATH  Google Scholar 

  38. Pritz T (1996) Analysis of four-parameter fractional derivative model of real solid materials. J Sound Vib 195:103–115

    Article  ADS  MATH  Google Scholar 

  39. Acierno D, La Mantia FP, Marrucci G, Titomanlio G (1976) A non-linear viscoelastic model with structure-dependent relaxation times: I—basic formulation. J Nonnewton Fluid Mech 1:125–146

    Article  Google Scholar 

  40. Acierno D, La Mantia FP, Marrucci G, Titomanlio G (1976) A non-linear viscoelastic model with structure-dependent relaxation times: II—Comparison with L.D. polyethylene transient stress. J Nonnewton Fluid Mech 1:147–157

    Article  Google Scholar 

  41. Green MS, Tobolsky AB (1946) A new approach to the theory of relaxing polymeric media. J Chem Phys 14:80–92

    Article  ADS  Google Scholar 

  42. Lodge AS, Yeen-Jing Wu (1971) Constitutive equations for polymer solutions derived from the bead/spring model of Rouse and Zimm. Rheol Acta 10:539–553

    MATH  Google Scholar 

  43. Mariucci G, Titomanlio G, Sarti GC (1973) Testing of a constitutive equation for entangled networks by elongational and shear data of polymer melts. Rheol Acta 12:269–275

    Article  Google Scholar 

  44. Meissner J (2009) Basic parameters, melt rheology, processing and end-use properties of three similar low density polyethylene samples. Pure Appl Chem 42:551–612

    Google Scholar 

  45. Meissner J (1972) Modifications of the Weissenberg rheogoniometer for measurement of transient rheological properties of molten polyethylene under shear: comparison with tensile data. Appl Polym Sci 16:2877–2899

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Dipartimento di Ingegneria Civile, Ambientale, Aerospaziale, dei Materiali (DICAM), Università degli Studi di Palermo, Viale delle Scienze, 90128, Palermo, Italy

    Salvatore Di Lorenzo, Mario Di Paola, Francesco Paolo La Mantia & Antonina Pirrotta

  2. Unit of Applied Mechanics, University of Innsbruck, 6020, Innsbruck, Austria

    Salvatore Di Lorenzo

  3. Department of Mathematical Sciences, University of Liverpool, Liverpool, UK

    Antonina Pirrotta

Authors
  1. Salvatore Di Lorenzo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mario Di Paola
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Francesco Paolo La Mantia
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Antonina Pirrotta
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mario Di Paola.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Di Lorenzo, S., Di Paola, M., La Mantia, F.P. et al. Non-linear viscoelastic behavior of polymer melts interpreted by fractional viscoelastic model. Meccanica 52, 1843–1850 (2017). https://doi.org/10.1007/s11012-016-0526-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-016-0526-8

Keywords

Search

Navigation