Effect of reinforcement, gravity and liquid loading on Rayleigh-type wave propagation

Abstract

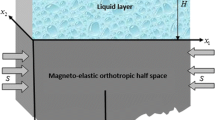
In the present time, self-reinforced materials are the basic requirement for civil engineering construction. These constructions encounter surface wave propagation during earthquakes and similar disturbances. Therefore, the study of surface wave propagation in such material is of great significance. The present paper, in the light of practical situation like dams, canals etc. aims to study the effect of gravity on the propagation of Rayleigh-type surface wave in a self-reinforced semi-infinite medium bounded and loaded by an inviscid liquid layer. Secular equation for the propagation of Rayleigh-type wave has been derived in closed form. The effect of gravity, reinforcement and liquid loading on phase velocity of Rayleigh-type wave has been distinctly observed. Numerical computation has been carried out and graphical illustration is provided for analysis of the presented study. Moreover, the effect of reinforced semi-infinite medium is compared to the effect of reinforced free semi-infinite medium on the phase velocity of Rayleigh-type surface wave to unravel the reinforcement effect. The effect of presence and absence of liquid loading on self-reinforced semi-infinite medium for Rayleigh-type wave propagation is also analysed and depicted by means of graphs.

Appendix

$$ \beta_{1}^{2} = \frac{{\mu_{L} }}{\rho }, $$

$$ \begin{aligned} \xi_{1} & = \lambda_{l} (1 - T^{2} )(1 - e^{ - 2TkH} ),\quad \xi_{2} = i(\lambda + \alpha ) - \eta_{1} s_{1} (\lambda + 2\mu_{T} ), \\ \xi_{3} & = i\left( {\lambda + \alpha } \right) - \eta_{2} s_{2} (\lambda + 2\mu_{T} ),\quad \xi_{4} = (\eta_{1} i - s_{1} )\mu_{L} ,\quad \xi_{5} = (\eta_{2} i - s_{2} )\mu_{L} , \\ \end{aligned} $$

$$ N_{1}^{{\prime }} = \left( {\rho V^{2} - P_{1} } \right)\left( {\rho V^{2} - \mu_{L} } \right), $$

$$ s_{j}^{{{\prime }2}} = \frac{{ - M_{1} \pm \sqrt {M_{1}^{2} - 4\mu_{L} P_{2} N_{1}^{{\prime }} } }}{{2\mu_{L} P_{2} }},\quad (j = 1,2) $$

$$ \eta_{j}^{\prime } = \frac{{s_{j}^{\prime 2} \mu_{L} + \rho V^{2} - P_{1} }}{{i\left( {s_{j}^{\prime } P_{2} } \right)}},\quad (j = 1,2) $$

$$ \begin{aligned} \xi_{1}^{{\prime }} & = \lambda_{l} (1 - T^{2} )(1 - e^{ - 2TkH} ),\quad \xi_{2}^{{\prime }} = i(\lambda + \alpha ) - \eta_{2}^{{\prime }} s_{2}^{{\prime }} (\lambda + 2\mu_{T} ),\quad \xi_{3}^{{\prime }} = i(\lambda + \alpha ) - \eta_{1}^{{\prime }} s_{1}^{{\prime }} (\lambda + 2\mu_{T} ), \\ \xi_{4}^{{\prime }} & = \left( {\eta_{1}^{{\prime }} i - s_{1}^{{\prime }} } \right)\mu_{L} ,\quad \xi_{5}^{{\prime }} = \left( {\eta_{2}^{{\prime }} i - s_{2}^{{\prime }} } \right)\mu_{L} , \\ \end{aligned} $$

$$ P_{1}^{{\prime }} = (\lambda + 2\mu ),\quad P_{2}^{{\prime }} = (\lambda + \mu ), $$

$$ M_{2} = \mu (\rho V^{2} - \mu ) + P_{1}^{{\prime }} \left( {\rho V^{2} - P_{1}^{{\prime }} } \right) - P_{2}^{{{\prime }2}} ,\quad N_{2} = \left( {\rho V^{2} - P_{1}^{{\prime }} } \right)(\rho V^{2} - \mu ) + \frac{{\rho^{2} g^{2} }}{{k^{2} }}, $$

$$ s_{j}^{2} = \frac{{ - M_{2} \pm \sqrt {M_{2}^{2} - 4\mu P_{1}^{{\prime }} N_{2} } }}{{2\mu P_{1}^{'} }},\quad (j = 3,4) $$

$$ \eta_{j} = \frac{{s_{j}^{2} \mu + \rho V^{2} - P_{1}^{{\prime }} }}{{i\left( {s_{j} P_{2}^{{\prime }} - \frac{\rho g}{k}} \right)}},\quad (j = 3,4), $$

$$ \begin{aligned} \chi_{1} & = \lambda_{l} (1 - T^{2} )(1 - e^{ - 2TkH} ),\quad \chi_{2} = i(\lambda + \alpha ) - \eta_{3} s_{3} (\lambda + 2\mu_{T} ), \\ \chi_{3} & = i(\lambda + \alpha ) - \eta_{4} s_{4} (\lambda + 2\mu_{T} ),\quad \chi_{4} = (\eta_{3} i - s_{3} )\mu_{L} ,\quad \chi_{5} = (\eta_{4} i - s_{4} )\mu_{L} , \\ \end{aligned} $$

$$ N_{2}^{{\prime }} = \left( {\rho V^{2} - P_{1}^{{\prime }} } \right)\left( {\rho V^{2} - \mu_{L} } \right), $$

$$ s_{j}^{{{\prime }2}} = \frac{{ - M_{2} \pm \sqrt {M_{2}^{2} - 4\mu P_{2}^{{\prime }} N_{2}^{{\prime }} } }}{{2\mu P_{2}^{{\prime }} }},\quad (j = 3,4) $$

$$ \eta_{j}^{\prime } = \frac{{s_{j}^{\prime 2} \mu + \rho V^{2} - P_{1}^{\prime } }}{{i\left( {s_{j}^{\prime } P_{2}^{\prime } } \right)}},\quad (j = 3,4) $$

$$ \begin{aligned} \chi_{1}^{{\prime }} & = \lambda_{l} (1 - T^{2} )(1 - e^{ - 2TkH} ),\quad \chi_{2}^{{\prime }} = i(\lambda ) - \eta_{3}^{{\prime }} s_{3}^{{\prime }} (\lambda + 2\mu ), \\ \chi_{3}^{{\prime }} & = i(\lambda ) - \eta_{4}^{{\prime }} s_{4}^{{\prime }} (\lambda + 2\mu ),\quad \chi_{4}^{{\prime }} = \left( {\eta_{3}^{{\prime }} i - s_{3}^{{\prime }} } \right)\mu ,\quad \chi_{5}^{{\prime }} = \left( {\eta_{4}^{{\prime }} i - s_{4}^{{\prime }} } \right)\mu , \\ \end{aligned} $$