Regular and chaotic vibration in a piezoelectric energy harvester

Abstract

We examine regular and chaotic responses of a vibrational energy harvester composed of a vertical beam and a tip mass. The beam is excited horizontally by a harmonic inertial force while mechanical vibrational energy is converted to electrical power through a piezoelectric patch. The mechanical resonator can be described by single or double well potentials depending on the gravity force from the tip mass. By changing the tip mass we examine bifurcations from single well oscillations, to regular and chaotic vibrations between the potential wells. The appearance of chaotic responses in the energy harvesting system is illustrated by the bifurcation diagram, the corresponding Fourier spectra, the phase portraits, and is confirmed by the 0–1 test. The appearance of chaotic vibrations reduces the level of harvested energy.

1 Introduction

Broadband energy harvesting systems for many applications are often nonlinear, exhibiting such nonlinear phenomena as material nonlinearities, geometrical nonlinearities, multi-scale responses and the appearance of multiple solutions. These phenomena can be observed from the nonlinear time series analysis of simulated mathematical models or from measured system responses in experiments. It is well known that the efficiency of many engineered systems may be enhanced by operation in a nonlinear regime. Nonlinear vibrational energy harvesting shows such an advantage, making possible broadband frequency vibration energy accumulation and transduction into useful electrical power output.

A range of vibration energy harvesting devices have been proposed [1–6]. The key aspect of nonlinear harvesters is the use of a double well potential function, so that the device will have two equilibrium positions [7–12]. Gammaitoni et al. [8] and Masana and Daqaq [13] highlighted the advantages of a double well potential for energy harvesting, particularly when inter well dynamics were excited. The Duffing oscillator model has been used for many energy harvesting simulations, with the addition of electromechanical coupling for the harvesting circuit [14, 15]. Electromagnetic harvesters with a cubic force nonlinearity have also been considered [16]. Litak et al. [17] and Ali et al. [18] investigated nonlinear piezomagnetoelastic energy harvesting under random broadband excitation. McInnes et al. [19] investigated the stochastic resonance phenomena for a nonlinear system with a double potential well. Gravitationally induced double potential wells in a system with a vertical elastic beam with a tip mass have been studied extensively [20, 23–25].

Recently, in the context of broad-band energy harvesting, bifurcations and chaotic vibrations have been studied in several papers. Cao et al. [26] studied chaos in the fractionally damped broadband piezoelectric energy generator in the system with additional magnets. Syta et al. [27] analysed the dynamic response of a piezoelectric material attached to a bistable laminate plate. It is worth to note that chaotic vibrations are, in most cases, characterized by moderate amplitude of vibrations and simultaneously give continuous spectrum of frequency, which can be useful to increase mechanical resonator durability.

In this article we discuss different solutions appearing in that system. Especially, intra- and inter-well oscillations as well as periodic and chaotic vibrations lead to different efficiency in the energy harvesting. Therefore, we identify the properties of given solutions by using nonlinear methods.

2 Mathematical model and equations of motion

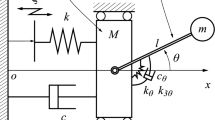
For nonlinear energy harvesting an inverted elastic beam is considered with a tip mass and the base is harmonically excited in the transverse direction. Only a summary of the equations is provided here; Friswell et al. [20] give a full derivation of the equations. Figure 1 shows the beam as a vertical cantilever of length L with harmonic base excitation $z(t) = z_0 \cos \omega t$. The beam carries a concentrated tip mass, $M_t$, with moment of inertia $I_t$, at the tip of the beam. The horizontal and vertical elastic displacements at the tip mass are v and u respectively, and s represents the distance along the neutral axis of the beam.

Fig. 1

Schematic of the inverted beam harvester. $M_t$ denotes the tip mass attached to the elastic beam, while v and u denote the horizontal and vertical displacements of the mass. P denotes an arbitrary point on the beam whose position is described by the coordinates s, $v_p$, and $u_p$. Piezoelectric patches are placed along the beam but are not shown here

In the following analysis the beam is assumed to have uniform inertia and stiffness properties; a non-uniform beam is easily modeled by including the mechanical beam properties in the energy integrals. The beam has cross sectional area A, mass density $\rho$, equivalent Young’s modulus E, and second moment of area I.

In this paper we assume that the tip mass is sufficiently large so that a single mode approximation of the beam deformation is sufficient. The displacement at any point in the beam is represented as a function of the tip mass displacement through a function for the beam deformation, $\psi (s)$, as

$$ v_p(s,t) = v_p(L,t) \psi (s) = v(t) \psi (s). $$

(1)

In this paper we will assume

$$ \psi (s) = 1 - \cos \left( \dfrac{\pi s}{2 L} \right) . $$

(2)

The equation of motion of the beam-mass system is derived in terms of the displacement of the tip mass using Lagrange’s equations [20–22] as

$$\begin{aligned}&\left[ N_5^2 I_t + M_t + \rho A N_1 + \left( \rho A N_3 + M_t N_4^2 + N_5^4 I_t \right) v^2 \right] \ddot{v} \\ &\quad + \,\left[ \rho A N_3 + M_t N_4^2 + N_5^4 I_t \right] v \dot{v}^2 \\&\quad +\, \left[ EI N_6 -N_9 \rho A g - N_4 M_t g + 2 EI N_7 v^2 \right] v \\ &\quad -\, \Theta _1 V - \Theta _2 v^2 V= - \left[ \rho A N_2 + M_t \right] \ddot{z} \end{aligned}$$

(3)

where the constants are given in the “Appendix”. Damping may also be added to these equations of motion, for example viscous, material or aerodynamic damping.

The model of the piezoelectric patches is now considered. The mechanical stiffness and mass density of the piezoelectric layers may be included in the beam constants already derived. The electromechanical coupling constants are

$$ \Theta _1 = \gamma _c \psi '(L_c) \quad \hbox {and} \quad \Theta _2 = \frac{1}{2} \gamma _c (\psi '(L_c))^3 $$

(4)

where $L_c$ is the active length of the piezoelectric material, which is assumed to start at the clamped end of the beam. For a unimorph configuration with excitation in the 31 mode, with thickness $h_c$ and width $b_c$, the constant $\gamma _c$ is

$$ \gamma _c = E_c d_{31} b_c \left( h + \dfrac{h_c}{2} - \bar{z} \right) $$

(5)

where h is the thickness of the beam, $d_{31}$ is the piezoelectric constant, $E_c$ is the Young’s modulus of the piezoelectric material and $\bar{z}$ is the effective neutral axis [28]. These expressions assume a monolithic piezoceramic actuator perfectly bonded to the beam; Bilgen et al. [29] considered the effect of the structure of a Macro-Fiber Composite (MFC) on the coupling coefficient, and also the effect of the bond and the insulating Kapton layers.

On the electrical side the piezoelectric patches may be considered as a capacitor, and the electrical circuit is represented by a resistive shunt connected across the piezoelectric patch. The electrical equation then becomes

$$ C_p \dot{V} + \frac{V}{R_l} + \Theta _1 \dot{v} + \Theta _2 v^2 \dot{v} = 0 $$

(6)

where $R_l$ is the load resistor and $C_p$ is the capacitance of the piezoelectric patch.

2.1 Equilibrium positions

The equilibrium positions with no forcing are obtained by setting the velocity and acceleration terms to zero in Eq. (3) to give,

$$ \left[ EI N_6 - N_9 \rho A g - N_4 M_t g + 2 EI N_7 v^2 \right] v = 0. $$

(7)

This equation has either one or three solutions, and $v=0$ is always a solution. Since $N_4>0$, there are three solutions if

$$ M_t > \dfrac{EI N_6 - N_9 \rho A g}{N_4 g} =M_{tb}, $$

(8)

where $M_{tb}$ is the tip mass so that the beam is about to buckle.

3 Numerical simulations and results

Following [20] we use the same set of system parameters, as given in Table 1. The beam-mass system is excited at the base with harmonic excitation. Figure 2 shows the equilibrium position of the tip mass, using the analysis described in Sect. 2.1, and shows that the post buckled response has two stable equilibrium positions above the critical tip mass $M_{tb}=10$ g. In the vicinity of these equilibrium points small amplitude vibrations can appear provided that excitation is also present. To observe its influence on the system dynamical response we used the harmonic base excitation at a fixed amplitude, $z_0$, and frequency, $f=\omega /(2 \pi )$ and varied the tip mass $M_t$. The corresponding bifurcation results are presented in Fig. 3. As expected the dynamical bifurcation pattern follows the split in the equilibrium positions, highlighting the significant change above the critical value tip mass $M_{tb}=10$ g. The character of the oscillations change by undergoing a series of bifurcations starting from the single frequency (in the limit for small $M_t$) to non-periodic vibrations (for relatively large $M_t$), that correspond to single point and a widely distributed set of points in the bifurcation diagram, respectively. Looking more closely at the bifurcation diagram, one can identify periodic windows characterised by distributions of discrete points among the non-periodic solutions. It is also possible that in this regions several solutions are present. However we used the same initial conditions for every frequency, and thus our approach was not able to capture all of the solutions simultaneously.

Table 1 Parameter values used in the simulation

Fig. 2

The effect of the tip mass on the equilibrium position. The dashed line denotes unstable equilibrium positions

Additionally, Fig. 4 shows the energy harvesting performance, i.e. the power output is plotted versus the tip mass. One can see that the power output increases above the value of $M_t$ corresponding to the critical buckling mass. Moreover the periodic windows visible in Fig. 3 give a higher power output.

Fig. 3

Bifurcation diagram of the displacement of the tip mass versus the tip mass for a base excitation of $z_0 = 16$ mm at frequency 0.5 Hz. The results were obtained using zero initial conditions for the tip mass displacement and velocity. Triangles indicate the cases used for more detailed studies, namely $M_t = 9.69$, 9.79, 10.19, 10.24, 10.39, and 10.59 g

Fig. 4

Average harvested power for the same conditions as shown in Fig. 3

Fig. 5

Time series for the tip mass displacement, corresponding velocity, and voltage for tip masses $M_t$ = 9.69 g (a), 9.79 g (b), 10.19 g (c), 10.24 g (d), 10.39 g (e), and 10.59 g (f)

Fig. 6

The corresponding Fourier spectra for $M_t$ = 9.79, 10.24, 10.39, and 10.59 g (for the cases b, d–f plotted in Fig. 5), starting from the top

Fig. 7

Phase portraits for $M_t$ = 9.79 g (b), 10.24 g (d), 10.39 g (e), and 10.59 g (f), from top right to left, respectively. The points correspond to the Poincaré maps. Note that the present plots are projections to the displacement–velocity plane for the tip mass

For better clarity we selected six values of $M_t$ marked by triangles in Figs. 3 and 4 corresponding to different solutions and calculated the corresponding time series of the displacement, velocity and the voltage output. The results are plotted in Fig. 5 for $M_t$ = 9.69, 9.79, 10.19, 10.24, 10.39, and 10.59 g, for Fig. 5a–f, respectively. One can easily see the evolution of the system response. Figure 5a shows a single frequency, while Fig. 5b shows symmetric oscillations with two frequencies indicating single well oscillations around the central equilibrium point (see Fig. 2). Figure 5c corresponds to a small amplitude single frequency non-symmetric solution indicating that the stable equilibrium point has already bifurcated. Finally, Fig. 5d–f show cross well oscillatory responses including periodic (Fig. 5e) and non-periodic cases (Fig. 5d, f). Furthermore, the displacement, velocity and voltage signals have the same generic nature. The non-periodicity in the kinematics are reflected in the voltage output (see Fig. 5d, f).

The cases b, d–f (cases numerated as in Fig. 5) are considered in more detail in the frequency domain by calculating the Fourier spectrum of the mechanical resonator displacement, as shown in Fig. 6. The corresponding phase portraits (the displacement–velocity phase portraits of the tip mass) are shown in Fig. 7. It should be noted that these qualitative measures clearly indicate the appearance of chaotic motion in cases d and f. Interestingly, the subharmonic visible in Fig. 5b corresponds to $f_1=0.167$ Hz, and this is one third of the excitation frequency $f=0.5$ Hz. The nature of this solution is illustrated in Fig. 7b with three loops in the phase portrait and three isolated Poincaré points. The chaotic solutions are characterised by strange attractors with complex trajectories and the wide distributions of the Poincaré points. It should, however, be noted that these plots are projections onto the displacement–velocity plane (neglecting the voltage coordinate).

The next step is to determine the quantitative parameter showing the chaotic character of the solutions. This can be done by means of the 0–1 test [30, 31] which is especially simple in systems with many degrees-of-freedom. The corresponding analysis and the estimation results will be presented in the next section.

4 The 0–1 test

The ‘0–1 test’, invented by Gottwald and Melbourne [30, 31], can be applied for any system of finite dimension to identify chaotic dynamics, but it is based on the statistical properties of a single coordinate only. Thus it is suitable to quantify the response where only one parameter is measured in time. The test is related to the universal properties of dynamical systems, such as spectral measures, and can therefore distinguish a chaotic system from a regular one using a single variable.

A particular advantage of the 0–1 test over the frequency spectrum is that it provides information regarding the dynamics in a single parameter value, similar to the Lyapunov exponent. However, the Lyapunov exponent can be difficult to estimate in any non-smooth simulated system or measured data [32]. Therefore the 0–1 test can provide a suitable algorithm to identify the chaotic solution [33, 36–38].

To start the analysis, we discretize the investigated time series $v(t) \rightarrow v(i)$ using the characteristic delay time $\delta t$ equal to one quarter of the excitation period $2 \pi / \omega$. This roughly indicates the vanishing of the mutual information [33, 39]. Starting from one of the initial map coordinate v(i), for sampling points $i=1,\ldots ,N$, we define new coordinates p(n) and q(n) as

$$\begin{aligned}&p(n) = \sum _{j=0}^{n} \frac{(v(j) - \overline{v})}{\sigma _v} \cos (j c), \\&q(n) = \sum _{j=0}^{n} \frac{v(j)- \overline{v})}{\sigma _v} \sin (j c), \end{aligned}$$

(9)

where $\overline{v}$ denotes the average value of v, $\sigma _v$ the corresponding standard deviation, and c is a constant $\in [0,\pi ]$. Note that q(n) is a complementary coordinate in the two dimensional space. Furthermore, starting from bounded coordinate v(i) we build a new series p(n) which can be either bounded or unbounded depending on the dynamics of the examined process.

Continuing the calculation procedure, the total mean square displacement is defined as

$$ M_c(n) = \lim _{N \rightarrow \infty } \frac{1}{N} \sum _{j=1}^N \left[ \left( p(j+ n) - p(j)\right) ^2 + \left( q(j+ n) -q(j)\right) ^2\right] . $$

(10)

The asymptotic growth of $M_c(n)$ can be easily characterised by the corresponding ratio $K'_c(n)$

$$ K'_c(n)= \frac{\ln (M(n))}{\ln n}. $$

(11)

In the limit as $n \rightarrow \infty$ (in present calculations $n =n_{max}=150$ while $N=1350$) we obtain the corresponding values of $K_c$ for a chosen value of c. Note, our choice of $n_{max}$ and N limits (in Eqs. 4, 5) is consistent with that proposed by Gottwald and Melbourne [34, 35, 40]. $N, n_{max} \rightarrow \infty$ but simultaneously $n_{max}$ should be about N/10.

It is important to note that the parameter c acts like a frequency in a spectral calculation. If c is badly chosen, it could resonate with the excitation frequency or its super- or sub- harmonics. In the 0–1 test, regular motion would yield an expanding behaviour in the (p, q)-plane [34] and the corresponding $M_c(n)$ has an asymptotic growth rate even for a regular system. The disadvantage of the test, its strong dependence on the chosen parameter c, can be overcome by a proposed modification. Gottwald and Melbourne [34, 36, 37] suggested randomly chosen values of c are taken and the median of the corresponding $K_c$-values are computed.

Consequently, the new covariance formulation is

$$ K_c= \frac{{\mathrm{cov}}({\mathbf{X}},{\mathbf{M}}_c)}{\sqrt{{\mathrm{var}}({\mathbf{X}}) {\mathrm{var}} ({\mathbf{M}}_c})}, $$

(12)

where vectors ${\mathbf{X}}=[1, 2, \ldots , n_{max}]$, and ${\mathbf{M}}_c= [M_c(1), M_c(2), \ldots , M_c(n_{max})]$.

In the above, the covariance ${\mathrm{cov}}({\mathbf{x}}, {\mathbf{y}})$ and variance ${\mathrm{var}}({\mathbf{x}})$, for arbitrary vectors ${\mathbf{x}}$ and ${\mathbf{y}}$ of $n_{max}$ elements, and the corresponding averages $\overline{x}$ and $\overline{y}$ respectively, are defined as

$$\begin{aligned}{\mathrm{cov}}({\mathbf{x}},{\mathbf{y}})&= \frac{1}{n_{max}} \sum _{n=1}^{n_{max}} (x(n)-\overline{x})(y(n)-\overline{y}), \\ {\mathrm{var}}({\mathbf{x}})&= {\mathrm{cov}}({\mathbf{x}}, {\mathbf{x}}). \end{aligned}$$

(13)

Finally, the median is taken of the $K_{c}$-values in Eq. (6), corresponding to 100 random values of $c \in (0,\pi )$. Such an average K-value can now be estimated for various tip masses, $M_t$.

Fig. 8

Average value of 0–1 test parameter, $\langle K\rangle$, versus the tip mass value. The corresponding limit in the summations (Eqs. 10, 13) were truncated at $n =n_{max}=150$ while $N=1350$. The triangles indicate the selected cases of $M_t$ studied in the previous section

Figure 8 shows $\langle K\rangle$ versus the tip mass. Here the chaotic solutions are clearly distinguished as $\langle K\rangle \approx 1$, from any type regular solutions where $\langle K\rangle \approx 0$. This is consistent with the previous qualitative methods based on the frequency spectrum (Fig. 6), phase portraits and the Poincaré maps (Fig. 7). It is worth noting that for all cases with maximal energy outputs (Fig. 4) their dynamical responses were periodic (Fig. 8).

5 Conclusions

The examined response vibrational energy harvester exhibited regular and chaotic oscillations. We have reported the corresponding transition in the system behaviour around the equilibrium bifurcation from a single point to two equilibrium points. We observe this transition by changing the tip mass. The system was excited by harmonic inertial force at a constant frequency, and the harvester responded at this frequency and also with additional subharmonics dependent on the value of the tip mass.

The mechanical vibrational energy was continuously converted to the electrical power through the piezoelectric patch. Interestingly, we observed the rise of the power output once the system changed from single well to cross barrier vibrations. Furthermore the appearance of the chaotic response lowered the power output considerably.

The bifurcation between regular and chaotic vibrations was reported using the bifurcation diagram, the corresponding Fourier spectra, and the phase portraits, and confirmed by the 0–1 test. We noticed that the appearance of chaotic vibrations significantly reduced the harvested energy.

Appendix

The constants $N_1$ to $N_9$ are given by

$$\begin{aligned} N_1&= \int _0^L{(\psi (s))^2 \hbox {d}s} = \left( \frac{3 \pi -8}{2\pi } \right) L, \\ N_2&= \int _0^L{\psi (s) \hbox {d}s} = \left( \frac{\pi -2}{\pi } \right) L, \\ N_3&= \int _0^L \left( \int _0^s (\psi '(\xi ))^2 \hbox {d}\xi \right) ^2 \hbox {d}s = \frac{\pi ^2 (2 \pi ^2-9)}{384} \frac{1}{L}, \quad \\ N_4&= \int _0^L (\psi '(s))^2 \hbox {d}s = \frac{\pi ^2}{8} \frac{1}{L}, \\ N_5&= \psi '(L) = \frac{\pi }{2} \frac{1}{L}, \\ N_6&= \int _0^L (\psi ''(s))^2 \hbox {d}s = \frac{\pi ^4}{32} \frac{1}{L^3} \\ N_7&= \int _0^L ( \psi '(s) \psi ''(s) )^2 \hbox {d}s = \frac{\pi ^6}{2^9} \frac{1}{L^5} \\ N_8&= \int _0^L (\psi '(s))^4 (\psi ''(s))^2 \hbox {d}s = \frac{\pi ^8}{4096} \frac{1}{L^7} \\ N_9&= \int _0^L \left[ \int _0^s (\psi '(\xi ))^2 \hbox {d}\xi \right] \hbox {d}s = - \frac{1}{4} + \frac{1}{16} \pi ^2 \end{aligned}$$

(14)