Axisymmetric motion of a porous sphere through a spherical envelope subject to a stress jump condition

Abstract

The flow problem of an incompressible axisymmetrical quasisteady translation and steady rotation of a porous sphere in an eccentric spherical container is discussed using a combined analytical–numerical technique. A continuity of velocity components and normal stress together with the stress jump condition for the tangential stress are used at the interface between porous and clear-fluid regions. The fluid flow outside the particle is governed by the classical Stokes equations while the fluid flow inside the porous region is treated by Brinkman model. In order to solve the Stokes equations for the flow field, a general solution is constructed from the superposition of the basic solutions in the two spherical coordinate systems based on both the porous sphere and spherical envelope. Solutions for translational and rotational motion of porous eccentric spherical particle in a spherical envelope are obtained using the boundary collocation technique. The hydrodynamic drag force and couple exerted by the surrounding fluid on the porous particle which is proportional to the translational and angular velocities, respectively, are calculated with good convergence for various values of the ratio of porous-to-container radii, the relative distance between the centers of the porous and container, the stress jump coefficient, and a coefficient that is proportional to the permeability. In the limits of the motions of a porous sphere in a concentric container and near a container surface with a small curvature, the numerical values of the normalized drag force and the normalized coupling coefficient are in good agreement with the available values in the literature.

Appendices

Appendix 1

The functions appearing in Eqs. (2.23)–(2.36) are defined as

$$A_{1n}(r,\theta )=-r^{-n-1}\,(n+1)\,{\mathfrak {I}}_{n+1}(\cos \theta )\,\csc \theta,$$

(4.7)

$$B_{1n}(r,\theta )=-r^{1-n}\,\left( (n+1)\,{\mathfrak {I}}_{n+1}(\cos \theta )\,\csc \theta -2{\mathfrak {I}}_{n}(\cos \theta )\,\cot \theta \right),$$

(4.8)

$$C_{1n}(r,\theta )=-r^{n-2}\,\left( (n+1)\,{\mathfrak {I}}_{n+1}(\cos \theta )\,\csc \theta -(2n-1)\,{\mathfrak {I}}_{n}(\cos \theta )\,\cot \theta \right) =E_{{1n}}(r,\theta ),$$

(4.9)

$$D_{1n}(r,\theta )=-r^{n}\,\left( (n+1)\,{\mathfrak {I}}_{n+1}(\cos \theta )\,\csc \theta -(2n+1)\,{\mathfrak {I}}_{n}(\cos \theta )\,\cot \theta \right),$$

(4.10)

$$F_{1n}(r,\theta )=r^{-3/2}\left( r\,\alpha \,I_{n-3/2}(r\,\alpha )\,{\mathfrak {I}}_{n}(\cos \theta )\,\cot \theta -(n+1)\,I_{n-1/2}(r\,\alpha )\,{\mathfrak {I}}_{n+1}(\cos \theta )\,\csc \theta \right),$$

(4.11)

$$A_{2n}(r,\theta )=-r^{-n-1}\,P_{n}(\cos \theta ),$$

(4.12)

$$B_{2n}(r,\theta )=-r^{1-n}\,\left( 2\,{\mathfrak {I}}_{n}(\cos \theta )+P_{n}(\cos \theta )\right),$$

(4.13)

$$C_{2n}(r,\theta )=-r^{n-2}\,\left( (2n-1)\,{\mathfrak {I}}_{n}(\cos \theta )+P_{n}(\cos \theta )\right) =E_{2n}(r,\theta ),$$

(4.14)

$$D_{2n}(r,\theta )=-r^{n}\,\left( (2n+1)\,{\mathfrak {I}}_{n}(\cos \theta )+P_{n}(\cos \theta )\right),$$

(4.15)

$$F_{2n}(r,\theta )=-r^{-3/2}\,\left( r\,\alpha \,I_{n-3/2}(r\,\alpha )\,{\mathfrak {I}}_{n}(\cos \theta )+I_{n-1/2}(r\,\alpha )\,P_{n}(\cos \theta )\right),$$

(4.16)

$$A_{3n}(r,\theta )=2\mu \,(n+1)\,r^{-n-2}\,P_{n-1}(\cos \theta ),$$

(4.17)

$$B_{3n}(r,\theta )=2\mu \,\left( n+1-\frac{3}{n}\right) \,r^{-n}\,P_{n-1}(\cos \theta ),$$

(4.18)

$$C_{3n}(r,\theta )=2\mu \,(2-n)\,r^{n-3}\,P_{n-1}(\cos \theta ),$$

(4.19)

$$D_{3n}(r,\theta )=-2\mu \,\left( n-2-\frac{3}{n-1}\right) \,r^{n-1}\,P_{n-1}(\cos \theta ),$$

(4.20)

$$E_{3n}(r,\theta )=\tilde{\mu }\,\left( 4-2n-\frac{\alpha ^2\,r^2}{n-1}\right) \,r^{n-3}\,P_{n-1}(\cos \theta ),$$

(4.21)

$$F_{3n}(r,\theta )=-2\tilde{\mu }\,r^{-5/2}\,\left( r\,\alpha \,I_{n+1/2}(r\,\alpha )+(n-2)\,I_{n-1/2}(r\,\alpha )\right) \,P_{n-1}(\cos \theta ),$$

(4.22)

$$A_{4n}(r,\theta )=2\mu \,(n^2-1)\,r^{-n-2}\,{\mathfrak {I}}_{n}(\cos \theta )\,\csc \theta,$$

(4.23)

$$B_{4n}(r,\theta )=2\mu \,n\,(n-2)\,r^{-n}\,{\mathfrak {I}}_{n}(\cos \theta )\,\csc \theta,$$

(4.24)

$$C_{4n}(r,\theta )=2\mu \,n\,(n-2)\,r^{n-3}\,{\mathfrak {I}}_{n}(\cos \theta )\,\csc \theta =\frac{\mu }{\tilde{\mu }}\,E_{{4n}}(r,\theta ),$$

(4.25)

$$D_{4n}(r,\theta )=2\mu \,(n^2-1)\,r^{n-1}\,{\mathfrak {I}}_{n}(\cos \theta )\,\csc \theta,$$

(4.26)

$$F_{4n}(r,\theta )=-\tilde{\mu }\,r^{-5/2}\left( 2r\,\alpha \,I_{n+1/2}(r\,\alpha )-(2n^2-4n+r^2\,\alpha ^2)\,I_{n-1/2}(r\,\alpha )\right) \,{\mathfrak {I}}_{n}(\cos \theta )\,\csc \theta,$$

(4.27)

$$A_{5n}(r,\theta )=A_{1n}(r,\theta )\,\tan \theta _2+A_{2n}(r,\theta ),$$

(4.28)

$$B_{5n}(r,\theta )=B_{1n}(r,\theta )\,\tan \theta _2+B_{2n}(r,\theta ),$$

(4.29)

$$C_{5n}(r,\theta )=C_{1n}(r,\theta )\,\tan \theta _2+C_{2n}(r,\theta ),$$

(4.30)

$$D_{5n}(r,\theta )=D_{1n}(r,\theta )\,\tan \theta _2+D_{2n}(r,\theta ),$$

(4.31)

$$E_{5n}(r,\theta )=\mu \,\xi \,\alpha /\eta \,\left( E_{1n}(r,\theta )\,\cos \theta _1-E_{2n}(r,\theta )\,\sin \theta _1\right) - E_{4n}(r,\theta),$$

(4.32)

$$F_{5n}(r,\theta )=\mu \,\xi \,\alpha /\eta \,\left( F_{1n}(r,\theta )\,\cos \theta _1-F_{2n}(r,\theta )\,\sin \theta _1\right) -F_{4n}(r,\theta ),$$

(4.33)

$$A_{6n}(r,\theta )=A_{1n}(r,\theta )\,\cot \theta _2-A_{2n}(r,\theta ),$$

(4.34)

$$B_{6n}(r,\theta )=B_{1n}(r,\theta )\,\cot \theta _2-B_{2n}(r,\theta ),$$

(4.35)

$$C_{6n}(r,\theta )=C_{1n}(r,\theta )\,\cot \theta _2-C_{2n}(r,\theta ),$$

(4.36)

$$D_{6n}(r,\theta )=D_{1n}(r,\theta )\,\cot \theta _2-D_{2n}(r,\theta ),$$

(4.37)

where $\eta =\sqrt{\mu /\tilde{\mu }}.$

1.1 Translation of a porous sphere in a concentric spherical container

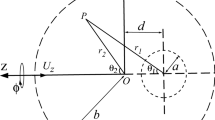
For appropriate comparison, we consider the quasisteady translational motion of a porous spherical particle of radius a in a concentric spherical envelope of radius b filled with an incompressible viscous fluid. We assume that the flow within the spherical container is Stokesian, and Brinkman’s model governs the flow inside the porous spherical particle. Under Stokes approximation the fundamental equation for the axisymmetric steady flow in terms of Stokes stream functions $\psi ^{e,i}$ for the outside and inside regions of the porous sphere satisfy Eqs. (2.7) and (2.8), respectively.

The boundary conditions used here are as follows:

At the interface between the homogeneous fluid and porous-medium regions ($r=1$):

Continuity of the velocity components

$$\psi ^{i}=\psi ^{e},$$

(4.38)

$$\frac{\partial \psi ^{i}}{\partial r}=\frac{\partial \psi ^{e}}{\partial r},$$

(4.39)

Continuity of the normal stress

$$p^{i}-p^{e}+\frac{2\mu }{\sin \theta }\,\frac{\partial }{\partial r}\left[ \frac{1}{r^2}\left( \frac{1}{\eta ^2}\,\frac{\partial \psi ^{i}}{\partial \theta }-\frac{\partial \psi ^{e}}{\partial \theta }\right) \right] =0.$$

(4.40)

As mentioned earlier, Ochoa-Tapia stress jump boundary condition for tangential stress given by

$$2r\,\frac{\partial }{\partial r}\left[ \frac{1}{r}\,\left( \frac{1}{\eta ^2}\,\frac{\partial \psi ^{i}}{\partial r}-\frac{\partial \psi ^{e}}{\partial r}\right) \right] +L_{-1}\left( \psi ^{e}-\frac{1}{\eta ^2}\,\psi ^{i}\right) =\frac{\xi \,\alpha }{\eta }\,\frac{\partial \psi ^{i}}{\partial \theta }.$$

(4.41)

On the envelope surface ($r=\lambda ^{-1}$):

Condition of impenetrability may be written as

$$\frac{\partial \psi ^{e}}{\partial \theta }-r^2\,U_z\,\cos \theta \,\sin \theta =0,$$

(4.42)

$$\frac{\partial \psi ^{e}}{\partial r}-r\,U_z\,\sin ^2\theta =0,$$

(4.43)

The suitable solutions for satisfying the boundary conditions on spherical surfaces for the stream functions, appropriate to the external and internal motions in the spherical coordinates, is given by [3]

$$\psi ^{e}=\left( A\,r^{-1}+B\,r+C\,r^2+D\,r^4\right) \,{\mathfrak {I}}_2(\cos \theta ),$$

(4.44)

$$\psi ^{i}=\left( E\,r^2+\sqrt{r}\,F\,I_{3/2}(\alpha \,r)\right) \,{\mathfrak {I}}_2(\cos \theta ),$$

(4.45)

where $A,\,B,\,C,\,D,\,E$ and F are arbitrary constants to be determined from the above boundary conditions (4.38)–(4.43).

The drag force is found to be

$$F_z=4\pi \,\mu \,a\,B=\frac{24\pi \,\mu \,U_z\,a\,\alpha }{\Delta _1}\,\left( 10\delta _1\,\delta _2\,\eta ^2+(\lambda ^5-1)\,[2\delta _1\,\delta _2\,(3\eta ^2+2)-\alpha ^3\,\delta _1-\delta _2\,\alpha ^2\,(2+\delta _1)]\right),$$

(4.46)

where

$$\begin{aligned} \Delta _1=\,& 4\left( 2\delta _1\,\delta _2\,\alpha \,(2+3\eta ^2) -\alpha ^4\,\delta _1-\delta _2\,\alpha ^3\,(2+\delta _1)\right) \,\lambda ^6 +9\left( \alpha ^4\,\delta _1+\delta _2\,\alpha ^3\,(2+\delta _1) +2\eta ^2\,\alpha ^2\,(3\delta _1-2)\right. \\&\left. +\,2\delta _1\,\delta _2\,\alpha \,(\eta ^2-2) +4\eta ^2\,\delta _1\,(2+3\eta ^2)\right) \,\lambda ^5 -10\left( \alpha ^4\,\delta _1+\delta _2\,\alpha ^3\,(2+\delta _1) +6\eta ^2\,\alpha ^2\,\delta _1\right. \\&\left. +\,2\delta _1\,\delta _2\,\alpha \,(3\eta ^2-2)\right) \,\lambda ^3 +9\left( \alpha ^4\,\delta _1+\delta _2\,\alpha ^3\,(2+\delta _1) +4\delta _1\,\delta _2\,\alpha \,(\eta ^2-1)\right) \,\lambda -4\alpha ^4\,\delta _1\\&-\,4\delta _2\,\alpha ^3\,(2+\delta _1)+6\eta ^2\,\alpha ^2\,(6+\delta _1) -2\delta _1\,\delta _2\,\alpha \,(9\eta ^2-8)+72\eta ^2\,\delta _1\,(\eta ^2-1). \end{aligned}$$

with $\delta _1=\Lambda \,\alpha ^2-3,\;\delta _2=2\xi \,\eta -\alpha,\;\Lambda =(\alpha \,\coth \alpha -1)^{-1}.$

As $\eta =1,$ i.e., the case of effective Brinkman viscosity equal to the fluid viscosity, the drag is given by

$$F_z=\frac{24\pi \,\mu \,U_z\,a\,\alpha }{\Delta _2}\,\left( 10\delta _1\,\delta _3+(\lambda ^5-1)\,[10\delta _1\,\delta _3-\alpha ^3\,\delta _1-\delta _3\,\alpha ^2\,(2+\delta _1)]\right),$$

(4.47)

where

$$\begin{aligned} \Delta _2=\, & {} 4\left( 10\delta _1\,\delta _3\,\alpha -\alpha ^4\,\delta _1 -\delta _3\,\alpha ^3\,(2+\delta _1)\right) \,\lambda ^6 +9\left( \alpha ^4\,\delta _1+\delta _3\,\alpha ^3\,(2+\delta _1) +2\alpha ^2\,(3\delta _1-2)\right. \\&\left. -\,2\delta _1\,\delta _3\,\alpha +20\delta _1\right) \,\lambda ^5 -10\left( \alpha ^4\,\delta _1+\delta _3\,\alpha ^3\,(2+\delta _1) +6\alpha ^2\,\delta _1+2\delta _1\,\delta _3\,\alpha \right) \,\lambda ^3\\&+\,9\left( \alpha ^4\,\delta _1 +\delta _3\,\alpha ^3\,(2+\delta _1)\right) \,\lambda -4\alpha ^4\,\delta _1 -4\delta _3\,\alpha ^3\,(2+\delta _1)+6\alpha ^2\,(6+\delta _1) -2\delta _1\,\delta _3\,\alpha. \end{aligned}$$

with $\delta _3=2\xi -\alpha.$ This agrees with the drag on the porous sphere case derived in [37]. Also, the same authors derived the drag force for $\xi =0$ (the continuity of the tangential stress at the porous-fluid interface).

When permeability k vanishes, i.e. permeability parameter $\alpha \rightarrow \infty,$ then the above model behave like a system of solid spherical particle in a spherical container. The hydrodynamic drag force in this case reduces to the following expression:

$$F_z=\frac{24\pi \,\mu \,U_z\,a\,(\lambda ^4+\lambda ^3+\lambda +1)}{(\lambda -1)^3\,(4\lambda ^2+7\lambda +4)}.$$

(4.48)

This result agrees with the earlier result [3].

Appendix 2

The functions appearing in Eqs. (3.14)–(3.16) are given by

$$a_{1n}(r,\theta )=r^{-n-1}\,P_{n}^1(\cos \theta ),$$

(4.49)

$$b_{1n}(r,\theta )=r^{n}\,P_{n}^1(\cos \theta ),$$

(4.50)

$$c_{1n}(r,\theta )=-r^{-1/2}\,I_{n+1/2}(r\,\alpha )\,P_{n}^1(\cos \theta ),$$

(4.51)

$$a_{2n}(r,\theta )=r^{-n-2}\,(n+2)\,P_{n}^1(\cos \theta ),$$

(4.52)

$$b_{2n}(r,\theta )=-r^{n-1}\,(1-n)\,P_{n}^1(\cos \theta ),$$

(4.53)

$$c_{2n}(r,\theta )=\eta ^{-2}\,r^{-3/2}\,\left( r\,\alpha \,I_{n+3/2}(r\,\alpha )-(1-n+r\,\xi \,\eta \,\alpha )\,I_{n+1/2}(r\,\alpha )\right) \,P_{n}^1(\cos \theta ),$$

(4.54)

$$a_{3n}(r,\theta )=\frac{1}{r_2\,\sin \theta _2}\,a_{1n}(r,\theta ),$$

(4.55)

$$b_{3n}(r,\theta )=\frac{1}{r_2\,\sin \theta _2}\,b_{1n}(r,\theta ).$$

(4.56)

1.1 Rotation of a porous sphere in a concentric spherical container

We now consider the steady rotational motion of a porous spherical particle of radius a located at the centre of a spherical vessel of radius b containing an incompressible viscous fluid. We have used the Brinkman’s model for the flow inside the porous sphere and Stokes model for the flow within the spherical container. The aim of this section is to obtain the hydrodynamic couple acting on the porous sphere in the presence of the container. The flow field in the porous region inside the porous sphere and in the clear region outside the porous sphere are still governed by Eqs. (3.3) and (3.5).

They must be solved subject to the following boundary conditions resulting from the continuity of velocity, and the stress jump condition at the porous-medium/clear fluid interface as well as the uniform velocity at the container surface:

At the fluid–porous interface ($r=1$):

$$q_\phi ^e=q_\phi ^i,$$

(4.57)

$$t_{r\phi }^i-t_{r\phi }^e=\frac{\xi \,\mu }{\sqrt{k}}\,q_\phi ^i.$$

(4.58)

On the container surface ($r=\lambda ^{-1}$):

$$q_\phi ^e=-\Omega _z\,a\,r\,\sin \theta.$$

(4.59)

The suitable solutions of the field Eqs. (3.3) and (3.5) for the present case, which are nonsingular everywhere in the flow outside and inside regions of the porous sphere [3], are

$$q_\phi ^e=\Omega _z\,a\,\left( A'\,r^{-2}+B'\,r\right) \,\sin \theta,$$

(4.60)

$$q_\phi ^i= \Omega _z\,a\,C'\,r^{-1/2}\,I_{3/2}(\alpha \,r)\,\sin \theta.$$

(4.61)

Moreover the corresponding shear stress components are given by

$$t_{r\phi }^e=-3\mu \,\Omega _z\,r^{-3}\,A'\,\sin \theta,$$

(4.62)

$$t_{r\phi }^i=\tilde{\mu }\,\Omega _z\,r^{-3}\,C'\,\left( \alpha \,r\,I_{1/2}(\alpha \,r)-3I_{3/2}(\alpha \,r)\right) \,\sin \theta.$$

(4.63)

The coefficients $A',\,B'$ and $C'$ are arbitrary constants to be determined from the above boundary conditions (4.57)–(4.59). Thus, we have

$$A'=\frac{\Delta _3}{(1-\lambda ^3)\,\Delta _3+3\eta ^2},$$

(4.64)

$$B'=-\frac{3\eta ^2+\Delta _3}{(1-\lambda ^3)\,\Delta _3+3\eta ^2},$$

(4.65)

$$C'=-\frac{3\alpha \,\eta ^2\,\Lambda ^3}{I_{1/2}(\alpha )\,[(1-\lambda ^3)\,\Delta _3+3\eta ^2]},$$

(4.66)

The hydrodynamic couple acting on the porous particle inside the spherical envelope is found to be

$$T_z=-8\pi \,\mu \,\Omega _z\,a^3\,A'=-\frac{8\pi \,\mu \,\Omega _z\,a^3\,\Delta _3}{(1-\lambda ^3)\,\Delta _3+3\eta ^2}.$$

(4.67)

If $\eta =1,$ the hydrodynamic couple acting on the porous sphere in a concentric spherical container with the stress jump boundary condition at the porous-fluid interface is reduced to

$$T_z=\frac{8\pi \,\mu \,\Omega _z\,a^3\,(3+\xi \,\alpha -\Lambda ^3\,\alpha ^2)}{(1-\lambda ^3)\,(\Lambda ^3\,\alpha ^2-\xi \,\alpha )+3\lambda ^3}.$$

(4.68)

which agrees with the result obtained in [38]. Also, for the steady rotational motion of a porous sphere in a spherical container with continuity of tangential stress ($\xi =0$), the expression for the hydrodynamic couple in this case reduces to the corresponding result of Saad [21].

In the limit $\alpha \rightarrow \infty$ (or $k=0$), the present system of porous particles reduces to that of a system of impermeable solid particles, and we have

$$T_z=\frac{8\pi \,\mu \,\Omega _z\,a^3}{1-\lambda ^3},$$

(4.69)

which is the well-known result [21].