Skip to main content
SpringerLink
Log in

Natural frequency analysis of functionally graded rectangular nanoplates with different boundary conditions via an analytical method

  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

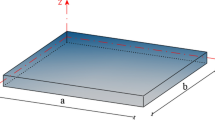
In this paper, the natural frequencies of a functionally graded nanoplate are analyzed for different combinations of boundary conditions. Application of new materials and specially the functionally graded materials in the micro- and nano-scale devices and systems is increasingly spread. Therefore, the study of the natural frequencies of functionally graded materials for different boundary conditions seems to be necessary in the micro/nano-structures. The article presented here covers broad types of common boundary conditions for the free vibration of functionally graded rectangular nanoplates for the first time. The analytical solution method used here is new for this subject and solves the governing equations with no approximation. The size dependency is considered according to Eringen’s differential form of nonlocal elasticity theory. The elasticity modulus and mass density of the plate are varied along the thickness of the plate according to a power-law distribution of the constituents’ volume fractions. As the in-plane and out-of-plane displacement variables are coupled in the equations of motion, a new exact solution method is introduced to solve the displacement fields analytically. The method is capable of dealing with new combinations of boundary conditions which have not been studied before in the literature. The validity and accuracy of the present method is investigated by comparing some of the present results to their counterparts reported in the literature. The results presented here are new and discussed for the first time in this subject. As a novelty a detailed study is carried out to examine the effects of power-law distribution, the characteristic internal length, the plate aspect ratio and the mode number on the natural frequencies of functionally graded rectangular plates for different boundary conditions. It’s shown that the type of boundary condition affects considerably on the values of natural frequency but the behavior of the frequency variations is in the same manner for different combinations of boundary conditions. These results can be used as benchmark for future studies.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Rahaeifard M, Kahrobaiyan MH, Ahmadian MT (2009) Sensitivity analysis of atomic force microscope cantilever made of functionally graded materials. Paper presented at the 3rd international conference on micro- and nano-systems

  2. Tighe TS, Worlock JM, Roukes ML (1997) Direct thermal conductance measurements on suspended monocrystalline nanostructures. Appl Phys Lett 70(20):2687–2689. doi:10.1063/1.118994

    Article  ADS  Google Scholar 

  3. Zalalutdinov MK, Baldwin JW, Marcus MH, Reichenbach RB, Parpia JM, Houston BH (2006) Two-dimensional array of coupled nanomechanical resonators. Appl Phys Lett. doi:10.1063/1.2190448

    Google Scholar 

  4. Waleed F, Eihab A-R, Ali N (2002) Mechanical behavior of an electrostatically actuated micropump. In: 43rd AIAA/ASME/ASCE/AHS/ASC structures, structural dynamics, and materials conference. Structures, structural dynamics, and materials and co-located conferences. American Institute of Aeronautics and Astronautics. doi:10.2514/6.2002-1303

  5. Zhang XM, Chau FS, Quan C, Lam YL, Liu AQ (2001) A study of the static characteristics of a torsional micromirror. Sens Actuators A Phys 90(1–2):73–81. doi:10.1016/S0924-4247(01)00453-8

    Article  Google Scholar 

  6. Xiaopeng Z, Eihab MA-R, Ali HN (2004) A reduced-order model for electrically actuated microplates. J Micromech Microeng 14(7):900

    Article  Google Scholar 

  7. Chong ACM, Yang F, Lam DCC, Tong P (2001) Torsion and bending of micron-scaled structures. J Mater Res 16(04):1052–1058

    Article  ADS  Google Scholar 

  8. Stölken JS, Evans AG (1998) A microbend test method for measuring the plasticity length scale. Acta Mater 46(14):5109–5115. doi:10.1016/S1359-6454(98)00153-0

    Article  Google Scholar 

  9. Baughman RH, Zakhidov AA, de Heer WA (2002) Carbon nanotubes–the route toward applications. Science (New York, NY) 297(5582):787–792. doi:10.1126/science.1060928

    Article  ADS  Google Scholar 

  10. Li C, Chou T-W (2003) A structural mechanics approach for the analysis of carbon nanotubes. Int J Solids Struct 40(10):2487–2499. doi:10.1016/S0020-7683(03)00056-8

    Article  MATH  Google Scholar 

  11. Li C, Chou T-W (2003) Single-walled carbon nanotubes as ultrahigh frequency nanomechanical resonators. Phys Rev B 68(7):073405

    Article  ADS  Google Scholar 

  12. Wang CM, Tan VBC, Zhang YY (2006) Timoshenko beam model for vibration analysis of multi-walled carbon nanotubes. J Sound Vib 294(4–5):1060–1072. doi:10.1016/j.jsv.2006.01.005

    Article  ADS  Google Scholar 

  13. Wang Q, Varadan VK (2006) Wave characteristics of carbon nanotubes. Int J Solids Struct 43(2):254–265. doi:10.1016/j.ijsolstr.2005.02.047

    Article  MATH  Google Scholar 

  14. Fleck NA, Hutchinson JW (1997) Strain gradient plasticity. In: John WH, Theodore YW (eds) Advances in applied mechanics, vol 33. Elsevier, Amsterdam, pp 295-361. doi:10.1016/S0065-2156(08)70388-0

  15. Zhou SJ, Li ZQ (2001) Length scales in the static and dynamic torsion of a circular cylindrical micro-bar. J Shandong Univ Technol 31:401–407

    Google Scholar 

  16. Yang F, Chong ACM, Lam DCC, Tong P (2002) Couple stress based strain gradient theory for elasticity. Int J Solids Struct 39(10):2731–2743. doi:10.1016/S0020-7683(02)00152-X

    Article  MATH  Google Scholar 

  17. Eringen AC (1983) On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J Appl Phys 54(9):4703–4710. doi:10.1063/1.332803

    Article  ADS  Google Scholar 

  18. Gibson RF, Ayorinde EO, Wen Y-F (2007) Vibrations of carbon nanotubes and their composites: a review. Compos Sci Technol 67(1):1–28. doi:10.1016/j.compscitech.2006.03.031

    Article  Google Scholar 

  19. Tounsi A, Heireche H, Berrabah HM, Benzair A, Boumia L (2008) Effect of small size on wave propagation in double-walled carbon nanotubes under temperature field. J Appl Phys. doi:10.1063/1.3018330

    Google Scholar 

  20. Lee H-L, Chang W-J (2008) Free transverse vibration of the fluid-conveying single-walled carbon nanotube using nonlocal elastic theory. J Appl Phys. doi:10.1063/1.2822099

    Google Scholar 

  21. Lu P, Lee HP, Lu C, Zhang PQ (2007) Application of nonlocal beam models for carbon nanotubes. Int J Solids Struct 44(16):5289–5300. doi:10.1016/j.ijsolstr.2006.12.034

    Article  MATH  Google Scholar 

  22. Wang CM, Zhang YY, Sai Sudha R, Kitipornchai S (2006) Buckling analysis of micro- and nano-rods/tubes based on nonlocal Timoshenko beam theory. J Phys D Appl Phys 39(17):3904

    Article  ADS  Google Scholar 

  23. Murmu T, Pradhan SC (2009) Small-scale effect on the vibration of nonuniform nanocantilever based on nonlocal elasticity theory. Phys E Low Dimens Syst Nanostruct 41(8):1451–1456. doi:10.1016/j.physe.2009.04.015

    Article  ADS  Google Scholar 

  24. Sarrami-Foroushani S, Azhari M (2014) Nonlocal vibration and buckling analysis of single and multi-layered graphene sheets using finite strip method including van der Waals effects. Phys E Low Dimens Syst Nanostruct 57:83–95. doi:10.1016/j.physe.2013.11.002

    Article  ADS  Google Scholar 

  25. Hosseini-Hashemi S, Zare M, Nazemnezhad R (2013) An exact analytical approach for free vibration of Mindlin rectangular nano-plates via nonlocal elasticity. Compos Struct 100:290–299. doi:10.1016/j.compstruct.2012.11.035

    Article  Google Scholar 

  26. Karamooz Ravari MR, Talebi S, Shahidi AR (2014) Analysis of the buckling of rectangular nanoplates by use of finite-difference method. Meccanica 49(6):1443–1455. doi:10.1007/s11012-014-9917-x

    Article  MathSciNet  MATH  Google Scholar 

  27. Witvrouw A, Mehta A (2005) The use of functionally graded poly-SiGe layers for MEMS applications. Mater Sci Forum 492–493:255–260

    Article  Google Scholar 

  28. Moser Y, Gijs MAM (2007) Miniaturized flexible temperature sensor. J Microelectromech Syst 16(6):1349–1354. doi:10.1109/JMEMS.2007.908437

    Article  Google Scholar 

  29. Hosseini-Hashemi S, Fadaee M, Atashipour SR (2011) A new exact analytical approach for free vibration of Reissner–Mindlin functionally graded rectangular plates. Int J Mech Sci 53(1):11–22. doi:10.1016/j.ijmecsci.2010.10.002

    Article  Google Scholar 

  30. Jomehzadeh E, Saidi AR, Atashipour SR (2009) An analytical approach for stress analysis of functionally graded annular sector plates. Mater Des 30(9):3679–3685. doi:10.1016/j.matdes.2009.02.011

    Article  MATH  Google Scholar 

  31. Ke L-L, Yang J, Kitipornchai S (2010) An analytical study on the nonlinear vibration of functionally graded beams. Meccanica 45(6):743–752. doi:10.1007/s11012-009-9276-1

    Article  MathSciNet  MATH  Google Scholar 

  32. Reddy JN (2011) Microstructure-dependent couple stress theories of functionally graded beams. J Mech Phys Solids 59(11):2382–2399. doi:10.1016/j.jmps.2011.06.008

    Article  ADS  MathSciNet  MATH  Google Scholar 

  33. Şimşek M, Reddy JN (2013) Bending and vibration of functionally graded microbeams using a new higher order beam theory and the modified couple stress theory. Int J Eng Sci 64:37–53. doi:10.1016/j.ijengsci.2012.12.002

    Article  MathSciNet  Google Scholar 

  34. Eltaher MA, Emam SA, Mahmoud FF (2012) Free vibration analysis of functionally graded size-dependent nanobeams. Appl Math Comput 218(14):7406–7420. doi:10.1016/j.amc.2011.12.090

    MathSciNet  MATH  Google Scholar 

  35. Rahmani O, Pedram O (2014) Analysis and modeling the size effect on vibration of functionally graded nanobeams based on nonlocal Timoshenko beam theory. Int J Eng Sci 77:55–70. doi:10.1016/j.ijengsci.2013.12.003

    Article  MathSciNet  Google Scholar 

  36. Ansari R, Gholami R, Faghih Shojaei M, Mohammadi V, Sahmani S (2013) Size-dependent bending, buckling and free vibration of functionally graded Timoshenko microbeams based on the most general strain gradient theory. Compos Struct 100:385–397. doi:10.1016/j.compstruct.2012.12.048

    Article  Google Scholar 

  37. Natarajan S, Chakraborty S, Thangavel M, Bordas S, Rabczuk T (2012) Size-dependent free flexural vibration behavior of functionally graded nanoplates. Comput Mater Sci 65:74–80. doi:10.1016/j.commatsci.2012.06.031

    Article  Google Scholar 

  38. Thai H-T, Kim S-E (2013) A size-dependent functionally graded Reddy plate model based on a modified couple stress theory. Compos B Eng 45(1):1636–1645. doi:10.1016/j.compositesb.2012.09.065

    Article  Google Scholar 

  39. Thai H-T, Choi D-H (2013) Size-dependent functionally graded Kirchhoff and Mindlin plate models based on a modified couple stress theory. Compos Struct 95:142–153. doi:10.1016/j.compstruct.2012.08.023

    Article  Google Scholar 

  40. Hosseini-Hashemi S, Bedroud M, Nazemnezhad R (2013) An exact analytical solution for free vibration of functionally graded circular/annular Mindlin nanoplates via nonlocal elasticity. Compos Struct 103:108–118. doi:10.1016/j.compstruct.2013.02.022

    Article  MATH  Google Scholar 

  41. Sahmani S, Ansari R (2013) On the free vibration response of functionally graded higher-order shear deformable microplates based on the strain gradient elasticity theory. Compos Struct 95:430–442. doi:10.1016/j.compstruct.2012.07.025

    Article  Google Scholar 

  42. Mohammadimehr M, Salemi M (2014) Bending and buckling analysis of functionally graded Mindlin nano-plate model based on strain gradient elasticity theory. Indian J Sci Res 1(2):587–598

    Google Scholar 

  43. Ansari R, Gholami R, Faghih Shojaei M, Mohammadi V, Sahmani S (2015) Bending, buckling and free vibration analysis of size-dependent functionally graded circular/annular microplates based on the modified strain gradient elasticity theory. Eur J Mech A Solids 49:251–267. doi:10.1016/j.euromechsol.2014.07.014

    Article  MathSciNet  Google Scholar 

  44. Salehipour H, Nahvi H, Shahidi AR (2015) Exact analytical solution for free vibration of functionally graded micro/nanoplates via three-dimensional nonlocal elasticity. Phys E Low Dimens Syst Nanostruct 66:350–358. doi:10.1016/j.physe.2014.10.001

    Article  ADS  Google Scholar 

  45. Reddy JN (2003) Mechanics of laminated composite plates and shells: theory and analysis, 2nd edn. Taylor & Francis, New York

    Google Scholar 

  46. Lu P, Zhang PQ, Lee HP, Wang CM, Reddy JN (2007) Non-local elastic plate theories. Proc R Soc A Math Phys Eng Sci 463(2088):3225–3240. doi:10.1098/rspa.2007.1903

    Article  ADS  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, Iran University of Science and Technology, 16842-13114, Narmak, Tehran, Iran

    Mojtaba Zare & Shahrokh Hosseini-Hashemi

  2. School of Engineering, Damghan University, 36716-41167, Damghan, Semnan, Iran

    Reza Nazemnezhad

  3. Center of Excellence in Railway Transportation, Iran University of Science and Technology, 16842-13114, Narmak, Tehran, Iran

    Shahrokh Hosseini-Hashemi

Authors
  1. Mojtaba Zare
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Reza Nazemnezhad
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Shahrokh Hosseini-Hashemi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mojtaba Zare.

Appendix: Characteristic determinant for different boundary conditions

Appendix: Characteristic determinant for different boundary conditions

SCSC:

$$ \left| {\begin{array}{*{20}c} 0 & 1 & 0 & 1 & 0 & 1 & 0 & 0 \\ {Sin[\eta \lambda_{1} ]} & {Cos[\eta \lambda_{1} ]} & {Sin[\eta \lambda_{2} ]} & {Cos[\eta \lambda_{2} ]} & {Sin[\eta \lambda_{3} ]} & {Cos[\eta \lambda_{3} ]} & 0 & 0 \\ 0 & {m\pi c_{1} } & 0 & {m\pi c_{2} } & 0 & {m\pi c_{3} } & {\lambda_{4} } & 0 \\ {m\pi Sin[\eta \lambda_{1} ]c_{1} } & {m\pi Cos[\eta \lambda_{1} ]c_{1} } & {m\pi Sin[\eta \lambda_{2} ]c_{2} } & {m\pi Cos[\eta \lambda_{2} ]c_{2} } & {m\pi Sin[\eta \lambda_{3} ]c_{3} } & {m\pi Cos[\eta \lambda_{3} ]c_{3} } & {Cos[\eta \lambda_{4} ]\lambda_{4} } & { - Sin[\eta \lambda_{4} ]\lambda_{4} } \\ {c_{1} \lambda_{1} } & 0 & {c_{2} \lambda_{2} } & 0 & {c_{3} \lambda_{3} } & 0 & 0 & {m\pi } \\ {Cos[\eta \lambda_{1} ]c_{1} \lambda_{1} } & { - Sin[\eta \lambda_{1} ]c_{1} \lambda_{1} } & {Cos[\eta \lambda_{2} ]c_{2} \lambda_{2} } & { - Sin[\eta \lambda_{2} ]c_{2} \lambda_{2} } & {Cos[\eta \lambda_{3} ]c_{3} \lambda_{3} } & { - Sin[\eta \lambda_{3} ]c_{3} \lambda_{3} } & {m\pi Sin[\eta \lambda_{4} ]} & {m\pi Cos[\eta \lambda_{4} ]} \\ {\lambda_{1} } & 0 & {\lambda_{2} } & 0 & {\lambda_{3} } & 0 & 0 & 0 \\ {Cos[\eta \lambda_{1} ]\lambda_{1} } & { - Sin[\eta \lambda_{1} ]\lambda_{1} } & {Cos[\eta \lambda_{2} ]\lambda_{2} } & { - Sin[\eta \lambda_{2} ]\lambda_{2} } & {Cos[\eta \lambda_{3} ]\lambda_{3} } & { - Sin[\eta \lambda_{3} ]\lambda_{3} } & 0 & 0 \\ \end{array} } \right| $$

SCSF:

$$ \left| {\begin{array}{*{20}c} {c_{1} \lambda_{1} } & 0 & {c_{2} \lambda_{2} } & 0 & {c_{3} \lambda_{3} } & 0 & 0 & {m\pi } \\ {Cos[\eta \lambda_{1} ]\;\left. \varPi \right|_{i = 1} } & { - Sin[\eta \lambda_{1} ]\;\left. \varPi \right|_{i = 1} } & {\left. {Cos[\eta \lambda_{2} ]\;\varPi } \right|_{i = 2} } & { - Sin[\eta \lambda_{2} ]\;\left. \varPi \right|_{i = 2} } & {Cos[\eta \lambda_{3} ]\;\left. \varPi \right|_{i = 3} } & { - Sin[\eta \lambda_{3} ]\;\left. \varPi \right|_{i = 3} } & {Sin[\eta \lambda_{4} ]\;\varGamma } & {Cos[\eta \lambda_{4} ]\;\varGamma } \\ 0 & {m\pi c_{1} } & 0 & {m\pi c_{2} } & 0 & {m\pi c_{3} } & {\lambda_{4} } & 0 \\ {Cos[\eta \lambda_{1} ]\;\left. \varOmega \right|_{i = 1} } & { - Sin[\eta \lambda_{1} ]\;\left. \varOmega \right|_{i = 1} } & {Cos[\eta \lambda_{2} ]\;\left. \varOmega \right|_{i = 2} } & { - Sin[\eta \lambda_{2} ]\;\left. \varOmega \right|_{i = 2} } & {Cos[\eta \lambda_{3} ]\;\left. \varOmega \right|_{i = 3} } & { - Sin[\eta \lambda_{3} ]\;\left. \varOmega \right|_{i = 3} } & {Sin[\eta \lambda_{4} ]\;\varUpsilon } & {Cos[\eta \lambda_{4} ]\;\varUpsilon } \\ {\lambda_{1} } & 0 & {\lambda_{2} } & 0 & {\lambda_{3} } & 0 & 0 & 0 \\ {Sin[\eta \lambda_{1} ]\;\left. \varPsi \right|_{i = 1} } & {Cos[\eta \lambda_{1} ]\;\left. \varPsi \right|_{i = 1} } & {Sin[\eta \lambda_{2} ]\;\left. \varPsi \right|_{i = 2} } & {Cos[\eta \lambda_{2} ]\;\left. \varPsi \right|_{i = 2} } & {Sin[\eta \lambda_{3} ]\;\left. \varPsi \right|_{i = 3} } & {Cos[\eta \lambda_{3} ]\;\left. \varPsi \right|_{i = 3} } & { - Cos[\eta \lambda_{4} ]A_{1} \;\varXi } & {Sin[\eta \lambda_{4} ]A_{1} \;\varXi } \\ 0 & 1 & 0 & 1 & 0 & 1 & 0 & 0 \\ {Sin[\eta \lambda_{1} ]\;\left. \varLambda \right|_{i = 1} } & {Cos[\eta \lambda_{1} ]\;\left. \varLambda \right|_{i = 1} } & {Sin[\eta \lambda_{2} ]\;\left. \varLambda \right|_{i = 2} } & {Cos[\eta \lambda_{2} ]\;\left. \varLambda \right|_{i = 2} } & {Sin[\eta \lambda_{3} ]\;\left. \varLambda \right|_{i = 3} } & {Cos[\eta \lambda_{3} ]\;\left. \varLambda \right|_{i = 3} } & { - Cos[\eta \lambda_{4} ]A_{0} \;\varXi } & {Sin[\eta \lambda_{4} ]A_{0} \;\varXi } \\ \end{array} } \right| $$

SFSF:

$$ \left| {\begin{array}{*{20}c} {\left. \varPi \right|_{i = 1} } & 0 & {\left. \varPi \right|_{i = 2} } & 0 & {\left. \varPi \right|_{i = 3} } & 0 & 0 & \varGamma \\ {Cos[\eta \lambda_{1} ]\;\left. \varPi \right|_{i = 1} } & { - Sin[\eta \lambda_{1} ]\;\left. \varPi \right|_{i = 1} } & {\left. {Cos[\eta \lambda_{2} ]\;\varPi } \right|_{i = 2} } & { - Sin[\eta \lambda_{2} ]\;\left. \varPi \right|_{i = 2} } & {Cos[\eta \lambda_{3} ]\;\left. \varPi \right|_{i = 3} } & { - Sin[\eta \lambda_{3} ]\;\left. \varPi \right|_{i = 3} } & {Sin[\eta \lambda_{4} ]\;\varGamma } & {Cos[\eta \lambda_{4} ]\;\varGamma } \\ {\left. \varOmega \right|_{i = 1} } & 0 & {\left. \varOmega \right|_{i = 2} } & 0 & {\left. \varOmega \right|_{i = 3} } & 0 & 0 & \varUpsilon \\ {Cos[\eta \lambda_{1} ]\;\left. \varOmega \right|_{i = 1} } & { - Sin[\eta \lambda_{1} ]\;\left. \varOmega \right|_{i = 1} } & {Cos[\eta \lambda_{2} ]\;\left. \varOmega \right|_{i = 2} } & { - Sin[\eta \lambda_{2} ]\;\left. \varOmega \right|_{i = 2} } & {Cos[\eta \lambda_{3} ]\;\left. \varOmega \right|_{i = 3} } & { - Sin[\eta \lambda_{3} ]\;\left. \varOmega \right|_{i = 3} } & {Sin[\eta \lambda_{4} ]\;\varUpsilon } & {Cos[\eta \lambda_{4} ]\;\varUpsilon } \\ 0 & {\;\left. \varPsi \right|_{i = 1} } & 0 & {\;\left. \varPsi \right|_{i = 2} } & 0 & {\;\left. \varPsi \right|_{i = 3} } & { - A_{1} \;\varXi } & 0 \\ {Sin[\eta \lambda_{1} ]\;\left. \varPsi \right|_{i = 1} } & {Cos[\eta \lambda_{1} ]\;\left. \varPsi \right|_{i = 1} } & {Sin[\eta \lambda_{2} ]\;\left. \varPsi \right|_{i = 2} } & {Cos[\eta \lambda_{2} ]\;\left. \varPsi \right|_{i = 2} } & {Sin[\eta \lambda_{3} ]\;\left. \varPsi \right|_{i = 3} } & {Cos[\eta \lambda_{3} ]\;\left. \varPsi \right|_{i = 3} } & { - Cos[\eta \lambda_{4} ]A_{1} \;\varXi } & {Sin[\eta \lambda_{4} ]A_{1} \;\varXi } \\ 0 & {\left. \varLambda \right|_{i = 1} } & 0 & {\left. \varLambda \right|_{i = 2} } & 0 & {\left. \varLambda \right|_{i = 3} } & { - A_{0} \;\varXi } & 0 \\ {Sin[\eta \lambda_{1} ]\;\left. \varLambda \right|_{i = 1} } & {Cos[\eta \lambda_{1} ]\;\left. \varLambda \right|_{i = 1} } & {Sin[\eta \lambda_{2} ]\;\left. \varLambda \right|_{i = 2} } & {Cos[\eta \lambda_{2} ]\;\left. \varLambda \right|_{i = 2} } & {Sin[\eta \lambda_{3} ]\;\left. \varLambda \right|_{i = 3} } & {Cos[\eta \lambda_{3} ]\;\left. \varLambda \right|_{i = 3} } & { - Cos[\eta \lambda_{4} ]A_{0} \;\varXi } & {Sin[\eta \lambda_{4} ]A_{0} \;\varXi } \\ \end{array} } \right| $$

SCSS:

$$ \left| {\begin{array}{*{20}c} 0 & 1 & 0 & 1 & 0 & 1 & 0 & 0 \\ {Sin[\eta \lambda_{1} ]} & {Cos[\eta \lambda_{1} ]} & {Sin[\eta \lambda_{2} ]} & {Cos[\eta \lambda_{2} ]} & {Sin[\eta \lambda_{3} ]} & {Cos[\eta \lambda_{3} ]} & 0 & 0 \\ 0 & {m\pi c_{1} } & 0 & {m\pi c_{2} } & 0 & {m\pi c_{3} } & {\lambda_{4} } & 0 \\ {m\pi Sin[\eta \lambda_{1} ]c_{1} } & {m\pi Cos[\eta \lambda_{1} ]c_{1} } & {m\pi Sin[\eta \lambda_{2} ]c_{2} } & {m\pi Cos[\eta \lambda_{2} ]c_{2} } & {m\pi Sin[\eta \lambda_{3} ]c_{3} } & {m\pi Cos[\eta \lambda_{3} ]c_{3} } & {Cos[\eta \lambda_{4} ]\lambda_{4} } & { - Sin[\eta \lambda_{4} ]\lambda_{4} } \\ {c_{1} \lambda_{1} } & 0 & {c_{2} \lambda_{2} } & 0 & {c_{3} \lambda_{3} } & 0 & 0 & {m\pi } \\ {Sin[\eta \lambda_{1} ]\;\left. \varPsi \right|_{i = 1} } & {Cos[\eta \lambda_{1} ]\;\left. \varPsi \right|_{i = 1} } & {Sin[\eta \lambda_{2} ]\;\left. \varPsi \right|_{i = 2} } & {Cos[\eta \lambda_{2} ]\;\left. \varPsi \right|_{i = 2} } & {Sin[\eta \lambda_{3} ]\;\left. \varPsi \right|_{i = 3} } & {Cos[\eta \lambda_{3} ]\;\left. \varPsi \right|_{i = 3} } & { - Cos[\eta \lambda_{4} ]A_{1} \;\varXi } & {Sin[\eta \lambda_{4} ]A_{1} \;\varXi } \\ {\lambda_{1} } & 0 & {\lambda_{2} } & 0 & {\lambda_{3} } & 0 & 0 & 0 \\ {Sin[\eta \lambda_{1} ]\;\left. \varLambda \right|_{i = 1} } & {\text{Cos} [\eta \lambda_{1} ]\;\left. \varLambda \right|_{i = 1} } & {Sin[\eta \lambda_{2} ]\;\left. \varLambda \right|_{i = 2} } & {\text{Cos} [\eta \lambda_{2} ]\;\left. \varLambda \right|_{i = 2} } & {Sin[\eta \lambda_{3} ]\;\left. \varLambda \right|_{i = 3} } & {\text{Cos} [\eta \lambda_{3} ]\;\left. \varLambda \right|_{i = 3} } & { - Cos[\eta \lambda_{4} ]A_{0} \;\varXi } & {Sin[\eta \lambda_{4} ]A_{0} \;\varXi } \\ \end{array} } \right| $$

SFSS:

$$ \left| {\begin{array}{*{20}c} {\left. \varPi \right|_{i = 1} } & 0 & {\left. \varPi \right|_{i = 2} } & 0 & {\left. \varPi \right|_{i = 3} } & 0 & 0 & \varGamma \\ {Sin[\eta \lambda_{1} ]} & {Cos[\eta \lambda_{1} ]} & {Sin[\eta \lambda_{2} ]} & {Cos[\eta \lambda_{2} ]} & {Sin[\eta \lambda_{3} ]} & {Cos[\eta \lambda_{3} ]} & 0 & 0 \\ {\left. \varOmega \right|_{i = 1} } & 0 & {\left. \varOmega \right|_{i = 2} } & 0 & {\left. \varOmega \right|_{i = 3} } & 0 & 0 & \varUpsilon \\ {m\pi Sin[\eta \lambda_{1} ]c_{1} } & {m\pi Cos[\eta \lambda_{1} ]c_{1} } & {m\pi Sin[\eta \lambda_{2} ]c_{2} } & {m\pi Cos[\eta \lambda_{2} ]c_{2} } & {m\pi Sin[\eta \lambda_{3} ]c_{3} } & {m\pi Cos[\eta \lambda_{3} ]c_{3} } & {Cos[\eta \lambda_{4} ]\lambda_{4} } & { - Sin[\eta \lambda_{4} ]\lambda_{4} } \\ 0 & {\;\left. \varPsi \right|_{i = 1} } & 0 & {\;\left. \varPsi \right|_{i = 2} } & 0 & {\;\left. \varPsi \right|_{i = 3} } & { - A_{1} \;\varXi } & 0 \\ {Sin[\eta \lambda_{1} ]\;\left. \varPsi \right|_{i = 1} } & {Cos[\eta \lambda_{1} ]\;\left. \varPsi \right|_{i = 1} } & {Sin[\eta \lambda_{2} ]\;\left. \varPsi \right|_{i = 2} } & {Cos[\eta \lambda_{2} ]\;\left. \varPsi \right|_{i = 2} } & {Sin[\eta \lambda_{3} ]\;\left. \varPsi \right|_{i = 3} } & {Cos[\eta \lambda_{3} ]\;\left. \varPsi \right|_{i = 3} } & { - Cos[\eta \lambda_{4} ]A_{1} \;\varXi } & {Sin[\eta \lambda_{4} ]A_{1} \;\varXi } \\ 0 & {\left. \varLambda \right|_{i = 1} } & 0 & {\left. \varLambda \right|_{i = 2} } & 0 & {\left. \varLambda \right|_{i = 3} } & { - A_{0} \;\varXi } & 0 \\ {Sin[\eta \lambda_{1} ]\;\left. \varLambda \right|_{i = 1} } & {Cos[\eta \lambda_{1} ]\;\left. \varLambda \right|_{i = 1} } & {Sin[\eta \lambda_{2} ]\;\left. \varLambda \right|_{i = 2} } & {Cos[\eta \lambda_{2} ]\;\left. \varLambda \right|_{i = 2} } & {Sin[\eta \lambda_{3} ]\;\left. \varLambda \right|_{i = 3} } & {Cos[\eta \lambda_{3} ]\;\left. \varLambda \right|_{i = 3} } & { - Cos[\eta \lambda_{4} ]A_{0} \;\varXi } & {Sin[\eta \lambda_{4} ]A_{1} \;\varXi } \\ \end{array} } \right| $$

SSSS:

$$ \left| {\begin{array}{*{20}c} 0 & 1 & 0 & 1 & 0 & 1 & 0 & 0 \\ {Sin[\eta \lambda_{1} ]} & {Cos[\eta \lambda_{1} ]} & {Sin[\eta \lambda_{2} ]} & {Cos[\eta \lambda_{2} ]} & {Sin[\eta \lambda_{3} ]} & {Cos[\eta \lambda_{3} ]} & 0 & 0 \\ 0 & {m\pi c_{1} } & 0 & {m\pi c_{2} } & 0 & {m\pi c_{3} } & {\lambda_{4} } & 0 \\ {m\pi Sin[\eta \lambda_{1} ]c_{1} } & {m\pi Cos[\eta \lambda_{1} ]c_{1} } & {m\pi Sin[\eta \lambda_{2} ]c_{2} } & {m\pi Cos[\eta \lambda_{2} ]c_{2} } & {m\pi Sin[\eta \lambda_{3} ]c_{3} } & {m\pi Cos[\eta \lambda_{3} ]c_{3} } & {Cos[\eta \lambda_{4} ]\lambda_{4} } & { - Sin[\eta \lambda_{4} ]\lambda_{4} } \\ 0 & {\;\left. \varPsi \right|_{i = 1} } & 0 & {\;\left. \varPsi \right|_{i = 2} } & 0 & {\;\left. \varPsi \right|_{i = 3} } & { - A_{1} \;\varXi } & 0 \\ {Sin[\eta \lambda_{1} ]\;\left. \varPsi \right|_{i = 1} } & {Cos[\eta \lambda_{1} ]\;\left. \varPsi \right|_{i = 1} } & {Sin[\eta \lambda_{2} ]\;\left. \varPsi \right|_{i = 2} } & {Cos[\eta \lambda_{2} ]\;\left. \varPsi \right|_{i = 2} } & {Sin[\eta \lambda_{3} ]\;\left. \varPsi \right|_{i = 3} } & {Cos[\eta \lambda_{3} ]\;\left. \varPsi \right|_{i = 3} } & { - Cos[\eta \lambda_{4} ]A_{1} \;\varXi } & {Sin[\eta \lambda_{4} ]A_{1} \;\varXi } \\ 0 & {\left. \varLambda \right|_{i = 1} } & 0 & {\left. \varLambda \right|_{i = 2} } & 0 & {\left. \varLambda \right|_{i = 3} } & { - A_{0} \;\varXi } & 0 \\ {Sin[\eta \lambda_{1} ]\;\left. \varLambda \right|_{i = 1} } & {\text{Cos} [\eta \lambda_{1} ]\;\left. \varLambda \right|_{i = 1} } & {Sin[\eta \lambda_{2} ]\;\left. \varLambda \right|_{i = 2} } & {\text{Cos} [\eta \lambda_{2} ]\;\left. \varLambda \right|_{i = 2} } & {Sin[\eta \lambda_{3} ]\;\left. \varLambda \right|_{i = 3} } & {\text{Cos} [\eta \lambda_{3} ]\;\left. \varLambda \right|_{i = 3} } & { - Cos[\eta \lambda_{4} ]A_{0} \;\varXi } & {Sin[\eta \lambda_{4} ]A_{0} \;\varXi } \\ \end{array} } \right| $$

In which:

$$ \begin{array}{l} \varPi = (A_{2} - A_{1} c_{i} )\lambda_{i} ( - m^{2} \pi^{2} ( - 2 + \nu ) + \lambda_{i}^{2} )\quad \varOmega = m\pi ( - 1 + \nu )(A_{1} - A_{0} c_{i} )\lambda_{i} \hfill \\ \varPsi = (A_{2} - A_{1} c_{i} )(m^{2} \pi^{2} \nu + \lambda_{i}^{2} )\quad \varLambda = (A_{1} - A_{0} c_{i} )(m^{2} \pi^{2} \nu + \lambda_{i}^{2} ) \hfill \\ \varGamma = m^{3} \pi^{3} ( - 1 + \nu )A_{1} \quad \varXi = m\pi ( - 1 + \nu )\lambda_{4} \quad \varUpsilon = \frac{( - 1 + \nu )}{2}A_{0} ( - m^{2} \pi^{2} + \lambda_{4}^{2} ) \hfill \\ \end{array} $$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zare, M., Nazemnezhad, R. & Hosseini-Hashemi, S. Natural frequency analysis of functionally graded rectangular nanoplates with different boundary conditions via an analytical method. Meccanica 50, 2391–2408 (2015). https://doi.org/10.1007/s11012-015-0161-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-015-0161-9

Keywords

Search

Navigation