Abstract
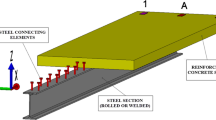
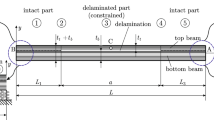
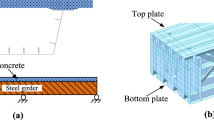
The end shear restraint, which is an un-classical type of end support, has a significant effect on the behavior of elastic composite beams. The principal aim of this paper is to present a numerical model for studying the effect of end shear restraint on static and free vibration behavior of elastic composite beams with various end conditions. The elastic composite beam, considered in this study, is composed of an upper concrete slab and a lower steel beam, connected at the interface by shear transmitting studs. This type of beam is widely used in constructions especially for highway bridges. The three types of end conditions considered in this study are simple, fixed and free supports. The numerical model is based on the combination of transfer matrix and analog beam methods. The field transfer matrices for the element of the elastic composite beam are derived. The present model is applied to the beam systems with and without end shear restraint and the static response and natural frequencies are calculated. the effect of shear stiffness between the upper slab and lower beam is also demonstrated.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Ranzi G, Zona A (2007) A steel–concrete composite beam model with partial interaction including the shear deformability of the steel component. Eng Struct 29:3026–3041
Ranzi G, Bradford MA, Uy B (2003) A general method of analysis of composite beams with partial interaction. Steel Compos Struct 3(3):169–184
Faella C, Martinelli E, Nigro E (2002) Steel and concrete composite beams with flexible shear connection: “exact” analytical expression of the stiffness matrix and applications. Comput Struct 80:1001–1009
Macorini L, Fragiacomo M, Amadio C, Izzuddin BA (2006) Long-term analysis of steel–concrete composite beams: FE modeling for effective width evaluation. Eng Struct 28:1110–1121
Ayoub A (2005) A force-based model for composite steel–concrete beams with partial interaction. J Construct Steel Res 61:387–414
Dilena M, Morassi A (2009) Vibrations of steel–concrete composite beams with partially degraded connection and applications to damage detection. J Sound Vibr 320:101–124
Gjelsvik A (1991) Analog-beam method for determining shear-lag effects. J Eng Mech 117(7):1575–1595
Betti R, Gjelsvik A (1996) Elastic composite beams. Comput Struct 59(3):437–451
Pestel EC, Leckie FA (1963) Matrix method in elastomechanics. McGraw-Hill, New York
Edward ED, Mark SS, Robert GL (1985) Combined finite element—transfer matrix method based on a mixed formulation. Comput Struct 20(3):173–180
Ohga M, Shigematsu T, Hara T (1991) Boundary element—transfer matrix method for plated structures. J Eng Mech 177(11):2509–2526
Geradin M, Chen SL (1995) An exact model reduction technique for beam structures: combination of transfer and stiffness matrices. J Sound Vib 185(3):431–440
Ellakany AM (2001) Static analysis of non-uniform elastic composite beams. Pakistan J Appl Sci 1(4):466–471
Ellakany AM, Elawadly Kh, Ellakany Ah (2001) Transfer matrix—analog beam method to calculate natural frequencies of elastic composite beams. In: Proceeding of the seventh international conference on computer aided optimum design of structures, Bologna, Italy, pp 259–268
Ellakany AM, Elawadly Kh, Elhamaky B (2004) A combined transfer matrix and analog beam method for free vibration analysis of composite beams. J Sound Vibr 227:765–781
Ellakany AM (2008) Calculation of higher natural frequencies of simply supported elastic composite beams using Riccati matrix method. Meccanica 43:523–532
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Ellakany, A.M., Tablia, H.A. A numerical model for static and free vibration analysis of elastic composite beams with end shear restraint. Meccanica 45, 463–474 (2010). https://doi.org/10.1007/s11012-009-9268-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11012-009-9268-1