Skip to main content
SpringerLink
Log in

On the Distribution of the Length of the Longest Increasing Subsequence in a Random Permutation

  • Published:
Methodology and Computing in Applied Probability Aims and scope Submit manuscript

Abstract

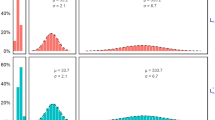
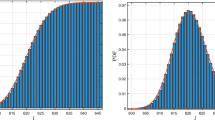
The distribution of the longest increasing subsequence in a random permutation has attracted many researchers in statistics, computer sciences and mathematics. There are considerable manuscripts studying the distribution especially for large n. In this short manuscript, we provide a simple probabilistic approach to obtain the exact distribution of the length of the longest increasing subsequence of a random permutation, based on the insertion procedure and the finite Markov chain imbedding technique.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Aldous D, Diaconis P (1995) Hammersley’s interacting particle process and longest increasing subsequences. Probab Theory Related Fields 103(2):199–213

    Article  MATH  MathSciNet  Google Scholar 

  2. Aldous D, Diaconis P (1999) Longest increasing subsequences: from patience sorting to the Baik-Deift-Johansson theorem. Bull Am Math Soc (NS) 36(4):413–432

    Article  MATH  MathSciNet  Google Scholar 

  3. Baer RM, Brock P (1968) Natural sorting over permutation spaces. Math Comput 22:385–410

    Article  MathSciNet  Google Scholar 

  4. Baik J, Deift P, Johansson K (1999) On the distribution of the length of the longest increasing subsequence of random permutations. J Am Math Soc 12(4):1119–1178

    Article  MATH  MathSciNet  Google Scholar 

  5. Fu J (2012) On the distribution of the number of occurrences of an order-preserving pattern of length three in a random permutation. Methodol Comput Appl Probab 14:831–842

    Article  MATH  MathSciNet  Google Scholar 

  6. Fu JC (1995) Exact and limiting distributions of the number of successions in a random permutation. Ann Inst Stat Math 47(3):435–446

    MATH  Google Scholar 

  7. Logan BF, Shepp LA (1977) A variational problem for random Young tableaux. Adv Math 26(2):206–222

    Article  MATH  MathSciNet  Google Scholar 

  8. Odlyzko AM, Rains EM (1998) On longest increasing subsequences in random permutations. Technical report, AT&T Labs

  9. Schensted C (1961) Longest increasing and decreasing subsequences. Can J Math 13:179–191

    Article  MATH  MathSciNet  Google Scholar 

  10. Ulam SM (1961) Monte Carlo calculations in problems of mathematical physics. In: Modern mathematics for the engineer: second series. McGraw-Hill, New York, pp 261–281

    Google Scholar 

  11. Vershik AM, Kerov SV (1977) Asymptotics of the plancherel measure of the symmetric group and the limiting form of young tables. Soviet Math Dokl 18:527–531. Translation of Dokl Acad Nauk SSSR 233:1024–1027

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Statistics, University of Manitoba, Winnipeg, MB, Canada, R3T 2N2

    James C. Fu & Yu-Fei Hsieh

Authors
  1. James C. Fu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yu-Fei Hsieh
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yu-Fei Hsieh.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Fu, J.C., Hsieh, YF. On the Distribution of the Length of the Longest Increasing Subsequence in a Random Permutation. Methodol Comput Appl Probab 17, 489–496 (2015). https://doi.org/10.1007/s11009-013-9376-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11009-013-9376-1

Keywords

AMS 2000 Subject Classification

Search

Navigation