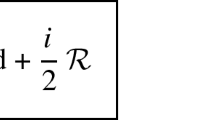Deformed $\sigma$-models, Ricci flow and Toda field theories

Abstract

It is shown that the Pohlmeyer map of a $\sigma$-model with a toric two-dimensional target space naturally leads to the ‘sausage’ metric. We then elaborate the trigonometric deformation of the $\mathbb {CP}^{n-1}$-model, proving that its T-dual metric is Kähler and solves the Ricci flow equation. Finally, we discuss a relation between flag manifold $\sigma$-models and Toda field theories.

1 Introduction and main results

The present paper is dedicated to two-dimensional $\sigma$-models with complex homogeneous target spaces and their deformations. By the results of [1,2,3,4], these models are classically integrable, at least in the sense that their e.o.m. admits a zero-curvature representation. This is a generalization and extension of the results about $\sigma$-models with symmetric target spaces, in particular projective spaces $\mathbb {CP}^{n-1}$ and Grassmannians Gr(k, n), that were widely studied in the 1980s [5,6,7,8,9,10,11,12,13]. (This is only an indicative list of references, as the literature on the subject is rather vast.) The complex homogeneous spaces are torus bundles over flag manifolds [14], and flag manifolds provide the basic and representative examples. The results of [4] (building on earlier work [15, 16]) provide a way of constructing the so-called trigonometric and elliptic deformations of these models. The trigonometric deformation, also known as the $\eta$-deformation, was first considered by Cherednik [17], extended and elaborated by Fateev [18] at the example of the principal chiral model, and substantially elucidated and generalized in the work of Klimčík [19,20,21]. In their work [22], Delduc, Magro and Vicedo constructed the $\eta$-deformation for the general case of symmetric target spaces, which is the setup relevant for the present paper. Further generalizations were proposed and elaborated later on in [23,24,25,26,27,28,29,30,31,32,33,34,35]. We should also mention that a lot of work has been dedicated to the study of the AdS/CFT applications of such deformations, cf. [37,38,39,40,41].

Below we mostly study the case of the trigonometrically deformed $\mathbb {CP}^{n-1}$ model. The corresponding manifold will be denoted $\mathbb {CP}^{n-1}_\eta$. In the case of $n=2$, and for a certain range of values of the deformation parameter $\eta$, the geometry is that of the so-called sausage [42]. In Sect. 2, we provide an alternative derivation of the model. We start with a most general two-dimensional target space with a U(1) isometry, in which case the geometry is described by a single function, which we call $g(\mu )$. It turns out that this function may be determined from the requirement of the integrability of the model. The first guess that comes to mind is that one could perform a dimensional reduction and require the integrability of the geodesic flow. For the two-dimensional geometry with a U(1) symmetry, this does not, however, impose any restrictions. Instead, we perform the Pohlmeyer reduction of the model [43] (perhaps more properly called the Pohlmeyer map in the case at hand) and require the integrability of its mechanical version. The reduction itself rules out certain classical solutions, such as geodesics, which are ‘trivially’ integrable anyway. The result of the analysis is that the integrable geometry turns out to be the ‘sausage,’ and a certain non-compact cousin thereof.

We view our derivation for $n=2$ as an empirical way of deducing the integrable geometry. For higher values of n, one could presumably follow the same route, but we leave this generalization for the future, and for the moment, we utilize the machinery of [22] to construct the $\eta$-deformed version of the $\mathbb {CP}^{n-1}$ model. We note that the analysis of this geometry has been undertaken in the recent papers [44,45,46]. In particular, it was noticed in [44] that it is useful to perform T-duality on all of the angles (the projective space, as well as its deformation, are toric manifolds), in order to get rid of the B-field. We will follow the same strategy here and mostly analyze the deformed model in the T-dual ‘frame.’ Sometimes, we refer to the dual geometry as $(\mathbb {CP}^{n-1}_\eta )^{\vee }$. We derive, in explicit form, the metric of the dual model, which is the subject of proposition 2. The second result, formulated as proposition 3, is that the dual manifold is Kähler (which is also a statement that ${\mathcal {N}}=(2, 2)$ supersymmetry [46] is preserved after T-duality). We obtain an explicit and compact expression for the Kähler potential, the main ingredient in this formula being the dilogarithm ${\mathrm {Li}}_2(z)$.

In our paper, we relate the $\eta$-deformed $\sigma$-models to the Ricci flow. There is vast mathematical and physical literature on the Ricci flow. A nice review of the history of the developments around the Ricci flow equation, in particular in low dimensions, may be found in [47]. Some other classic works on the subject (in three and two dimensions, respectively) are [48, 49]. One may also consult [51] as a concise general review of the theory of Ricci flow. Integrable structures of the Ricci flow equation for two-dimensional target spaces, related to the so-called continual Toda system, were found in [50, 51]. Similar integrable structures have been used to find solutions of the supergravity equations of motion [52]. Ricci flow has also been recently discussed in the context of the swampland distance conjectures [53]. Here, we will show that, after a linear change of variables, the metric of the dual space $(\mathbb {CP}^{n-1}_\eta )^{\vee }$ satisfies the pure¹ Kähler Ricci flow equation (proposition 4). The flow parameter, i.e., the time $\tau$ in this equation, is related to the deformation parameter $\eta$ in a simple way. The results of [54, 55] then imply that the Ricci flow equation is satisfied in the original frame as well, this time with a dilaton and a nonzero B-field.² The important role of the emerging dilaton is in the analysis of the effects of the Ricci flow on the metric: One has to take into account that the coordinates that were left intact by the Ricci flow in the T-dual frame start ‘running’ (depending on $\tau$) in the original frame, due to the presence of the dilaton. One has to take this into account in analyzing the asymptotic behavior of the metric under the Ricci flow.

In Sect. 3.5, we point out that the recent work of Costello and Yamazaki [4] paves a way to constructing another integrable deformation of the $\mathbb {CP}^{n-1}$ model and indeed of other models with complex homogeneous target spaces. This approach uses the language of $\beta \gamma$-systems. In fact, in this framework one quickly arrives at the flag manifold $\sigma$-models and related models introduced in [1,2,3]. As it has been shown in the recent work [58], the Lax connections of a class of models closely related to these ones have ultra-local Poisson brackets. On the other hand, at least for $\mathbb {CP}^{n-1}$ the deformation based on the $\beta \gamma$-system formulation is different from the $\eta$-deformation, unless $n=2$. Perhaps, this is due to the fact that the $\beta \gamma$-systems feature an anomaly in these cases, and the corresponding models might not be well-defined quantum-mechanically. In view of this it is interesting, whether the ultralocal Poisson structure may be preserved for the $\eta$-deformed models when $n>2$. (For $n=2$, the answer is affirmative [59, 60].)

Finally, in Sect. 4 we turn to the discussion of the flag manifold $\sigma$-models of [1,2,3]. We consider an analogue of ‘Pohlmeyer map’ for these models. Whereas in the $\mathbb {CP}^1$-case this leads to a sin-Gordon model, in the case of complete flags $U(n)\over U(1)^n$ we obtain a field-theoretic incarnation of a (periodic) Toda chain, interacting with some additional fields, which we call $U_{ij}$. When $U_{ij}=0$, we obtain a pure Toda field theory, and the map is the one that has been discussed in the math literature in the context of special harmonic maps (called primitive maps) to flag manifold target spaces [61, 62]. Our approach provides an embedding of these rather special maps into a full-fledged $\sigma$-model, with a non-topological B-field. If one drops the $U_{ij}$ fields, the zero-curvature representation for the $\sigma$-model reduces to the Lax pair of Flaschka–Manakov type.

Notation Throughout the paper, the worldsheet $\Sigma$ will be assumed a Riemann surface, with complex coordinates $z, {\overline{z}}$. Derivatives with respect to these coordinates will be denoted $\partial :=\partial _z$ and ${\overline{\partial }}:=\partial _{{\overline{z}}}$. We will also make use of worldsheet covariant derivatives, acting on sections of $T{\mathcal {M}}\big |_{\Sigma }$, i.e., on target space vectors restricted to the worldsheet, and these will be denoted $\nabla :=\nabla _z$ and $\overline{\nabla }:=\nabla _{{\overline{z}}}$. Similar notation is adopted for all other covariant derivatives, whose meaning is explained later on, i.e., $D, {\overline{D}}, {\mathscr {D}}, \overline{{\mathscr {D}}}$.

2 Target space with a U(1)-isometry: the Pohlmeyer map

To start with, we consider $\sigma$-models with a two-dimensional target space, i.e., maps $X: \Sigma \rightarrow {\mathcal {M}}_2$, where $\Sigma =\Sigma _2$ is the worldsheet and ${\mathcal {M}}_2$ is the target-space with a U(1)-isometry. In particular, the metric on ${\mathcal {M}}_2$ has the form (in toric coordinates)

Here, $g^{-1}=H_{\mu \mu }$ may be understood as the second derivative of a ‘symplectic potential’ $H(\mu )$, $\mu$ being the moment map for the U(1)-action. In this section, we will not need this detail, but we will return to it in Sect. 3.2 in the discussion of higher-dimensional toric manifolds.

We wish to decide, for which geometries (i.e., for which functions $g(\mu )$) the $\sigma$-model associated with the above metric is classically integrable. The first thing to note is that the direct mechanical reduction of the model does not give any clues, as the resulting mechanical system is integrable for any $g(\mu )$. Indeed, it possesses two integrals of motion: the energy and the angular momentum (corresponding to the shifts of $\phi$). For this reason, we will take another route and look at the generalized Pohlmeyer reduction of the model.

Following the original approach of Pohlmeyer [43], we may set

$$\begin{aligned} G_{ij}\,\partial X^i \partial X^j=1=G_{ij}\,{\overline{\partial }}X^i {\overline{\partial }}X^j, \end{aligned}$$

(2.2)

using conformal invariance of the $\sigma$-model action. An analogue of the Cauchy–Schwarz inequality for the complex vector $\partial X^i$ implies $G_{ij}\,\partial X^i {\overline{\partial }}X^j\ge 1$; therefore,

$$\begin{aligned} G_{ij}\,\partial X^i {\overline{\partial }}X^j=\cosh {\chi }. \end{aligned}$$

(2.3)

The equations of motion of the $\sigma$-model have the form $\overline{\nabla }\nabla X^j=0$.

We will now derive the equation of motion for the field $\chi$. In the undeformed case, when ${\mathcal {M}}_2=S^2$ is a sphere, this equation is the sinh-Gordon equation, as observed by Pohlmeyer.³

Proposition 1

Suppose the e.o.m. of the $\sigma$-model with metric (2.1), as well as the Pohlmeyer conditions (2.2), are satisfied. Then, $\chi (z, {\overline{z}}), \;\mu (z, {\overline{z}})$ satisfy the equations

$$\begin{aligned}&{\overline{\partial }}\partial \chi -2g''(\mu )\,\sinh {\chi }=0 \end{aligned}$$

(2.4)

$$\begin{aligned}&\partial {\overline{\partial }}\mu -2\,g'(\mu )\, \cosh {\chi }=0. \end{aligned}$$

(2.5)

Proof

First of all, let us assume that the vectors $\partial X^i$ and ${\overline{\partial }}X^i$ are linearly independent at generic points. In this case, since the target space is two-dimensional, we may decompose any vector field $v\big |_\Sigma$ in this basis. For example,

$$\begin{aligned} \nabla ^2 X^i=a_z\,\nabla X^i+b_z\,\overline{\nabla }X^i. \end{aligned}$$

(2.6)

To calculate the coefficients, we take scalar products with the respective vectors and use the conditions (2.2), as well as the e.o.m. for $X^i$ (the brackets $\langle \bullet , \bullet \rangle$ indicate the scalar product w.r.t. the metric $G_{ij}$):

$$\begin{aligned}&\langle \nabla X, \nabla ^2 X \rangle ={1\over 2}\partial \langle \nabla X, \nabla X \rangle =0=a_z+b_z\,\cosh {\chi } \end{aligned}$$

(2.7)

$$\begin{aligned}&\langle \overline{\nabla }X, \nabla ^2 X \rangle =\partial (\cosh {\chi })=a_z\,\cosh {\chi }+b_z. \end{aligned}$$

(2.8)

One finds

$$\begin{aligned} a_z=\partial \chi \cdot \frac{\cosh {\chi }}{\sinh {\chi }},\quad \quad b_z=-\frac{\partial \chi }{\sinh {\chi }}. \end{aligned}$$

(2.9)

Analogously

$$\begin{aligned}&\overline{\nabla }^2 X^i=a_{{\overline{z}}}\,\nabla X^i+b_{{\overline{z}}}\,\overline{\nabla }X^i, \end{aligned}$$

(2.10)

$$\begin{aligned}&{\text {where}}\quad \quad a_{{\overline{z}}}=-\frac{{\overline{\partial }}\chi }{\sinh {\chi }},\quad \quad b_{{\overline{z}}}={\overline{\partial }}\chi \cdot \frac{\cosh {\chi }}{\sinh {\chi }}. \end{aligned}$$

(2.11)

To derive the e.o.m. of $\chi$, we compute the mixed derivative ${\overline{\partial }}\partial$ of the definition $\langle \overline{\nabla }X, \nabla X \rangle =\cosh {\chi }$:

$$\begin{aligned} \cosh {\chi }\,{\overline{\partial }}\chi \, \partial \chi +\sinh {\chi }\,\partial {\overline{\partial }}\chi =\langle \overline{\nabla }^2X, \nabla ^2 X\rangle +\langle \overline{\nabla }X, \overline{\nabla }\nabla ^2 X\rangle . \end{aligned}$$

(2.12)

From (2.6) and (2.10), we see that the first terms in both sides are equal. On the other hand, for the last term we use the following identity:

$$\begin{aligned} \overline{\nabla }\nabla ^2 X^i=[\overline{\nabla }, \nabla ] \nabla X^i+\nabla \overline{\nabla }\nabla X^i=R^i_{\;mkn}\;\overline{\nabla }X^k\,\nabla X^m\,\nabla X^n, \end{aligned}$$

(2.13)

where R is the Riemann tensor of metric (2.1). For a two-dimensional target space with complex coordinate w and line element $ds^2=\Omega \,dw\,d{\overline{w}}$, we get $R_{w{\overline{w}}w{\overline{w}}}={\Omega \over 2} \,\overline{\partial }\partial \log {\Omega }$ and

$$\begin{aligned} \langle \overline{\nabla }X, \overline{\nabla }\nabla ^2 X\rangle =-{1\over 8}\Omega ^2 \left( {\overline{\partial }}w \partial {\overline{w}}-\partial w {\overline{\partial }}{\overline{w}}\right) ^2\,R\,, \end{aligned}$$

(2.14)

where R is the scalar curvature $R=-4\,\Omega ^{-1}\,\overline{\partial }\partial \log {\Omega }$. Since ${\Omega \over 2} \left( {\overline{\partial }}w \partial {\overline{w}}+\partial w {\overline{\partial }}{\overline{w}}\right) =\cosh {\chi }$, taking into account (2.2), we find

$$\begin{aligned} \langle \overline{\nabla }X, \overline{\nabla }\nabla ^2 X\rangle =-{1\over 2}\,\sinh ^2{\chi }\,R, \end{aligned}$$

(2.15)

and therefore, the e.o.m. for $\chi$ takes the form

$$\begin{aligned} {\overline{\partial }}\partial \chi +{1\over 2}\,R\,\sinh {\chi }=0. \end{aligned}$$

(2.16)

In fact, so far we have not made use of the toric structure (2.1) of the target space. Now, for the toric metric (2.1) the scalar curvature is

$$\begin{aligned} R=-4\,\frac{d^2 g}{d\mu ^2}. \end{aligned}$$

(2.17)

For example, in the case of a sphere $g={1\over 2}(1-\mu ^2)$, so that the scalar curvature $R=4$ (compatible with the Gauss–Bonnet formula ${1\over 4\pi }\,\int \,{1\over 2}\,d\mu \,d\phi \,R=2$), and one arrives at the sinh-Gordon equation. In all other cases, however, $R=R(\mu )$ is a non-constant function, and therefore, the equation for $\chi$ involves the target-space field $\mu$. One therefore needs to write out the e.o.m. for $\mu$, which easily follows from the $\sigma$-model action with metric (2.1):

$$\begin{aligned} \partial {\overline{\partial }}\mu -2\,g'\, \cosh {\chi }=0. \end{aligned}$$

(2.18)

Here, we also used definition (2.3) of $\chi$. (For completeness, we also record the e.o.m. for the remaining target-space variable $\phi$: ${\overline{\partial }}(g(\mu )\,\partial \phi )+\partial (g(\mu )\,{\overline{\partial }}\phi )=0.$) $\square$

Now, equations (2.16) and (2.18) follow from a single Lagrangian

$$\begin{aligned} {\mathscr {L}}={1\over 2 } \partial \mu {\overline{\partial }}\mu +{1\over 2} \partial \chi {\overline{\partial }}\chi +f(\mu )\,\cosh {\chi } \end{aligned}$$

(2.19)

if the following conditions are satisfied: $f=-{R\over 2}=2g''$, $f'=2 g'$, which leads to the equation $f''-f=0$. As a result, $f=2a_1 \,e^\mu +2a_2\, e^{-\mu }$. The function $g(\mu )$ entering metric (2.1) is

$$\begin{aligned} g(\mu )=b+a_1\, e^{ \mu }+a_2\, e^{-\mu }, \end{aligned}$$

(2.20)

where $a_1, a_2, b$ are apriori arbitrary constants. Interestingly, for certain choices of these parameters the corresponding metric corresponds to the so-called sausage (an elongated sphere). For the moment, let us assume that ${\mathrm {sgn}}(a_1)={\mathrm {sgn}}(a_2)$, in which case, by a rescaling and shift of $\mu$, we can bring the function g to the form

$$\begin{aligned} g(\mu )=b+a\,\cosh {\mu }. \end{aligned}$$

(2.21)

If we wish ${\mathcal {M}}_2$ to be of finite volume, we should assume that the function $g(\mu )$ has two zeros, $g(\pm \mu _0)=0$. Provided the angle $\phi$ has periodicity $2\pi$, the non-singularity at these points requires that $g'(\pm \mu _0)=\mp 1$. This leads to the conditions $b+a\,\cosh {\mu _0}=0,\; a\,\sinh {\mu _0}=-1$, i.e.,

Metric (2.1) with this function $g(\mu )$ is the so-called sausage geometry [42], which is a deformation of the round sphere $S^2$. Here, $\mu _0$ is the deformation parameter, and the round sphere metric is recovered in the limit $\mu _0\rightarrow 0, \mu =\mu _0 \widetilde{\mu }$, with $\widetilde{\mu }\in [-1, 1]$.

We obtained the above results by requiring that the $\mu , \chi$-equations follow from a single Lagrangian. One could argue that this requirement is too stringent, since it is known that typically Pohlmeyer’s reduction may lead to non-Lagrangian equations [63]. A justification is that our goal is to understand, whether the original (and hence the resulting) model is integrable. One simple check of this consists in performing a mechanical reduction. For the mechanical system, however, the requirement that the two equations follow from a single Lagrangian is the same as the requirement that the system possesses an integral of motion, the energy. Miraculously, the second integral of motion, necessary for a system with two degrees of freedom, appears automatically. Indeed, let us write out the Lagrangian (2.19) for the function $f(\mu )=2a\,\cosh {\mu }$:

$$\begin{aligned} {\mathscr {L}}= & {} {1\over 2} \partial \mu {\overline{\partial }}\mu +{1\over 2} \partial \chi {\overline{\partial }}\chi +2a\,\cosh {\mu }\,\cosh {\chi } \end{aligned}$$

(2.23)

$$\begin{aligned}= & {} \left( {1\over 2} \partial \widetilde{\mu } \,{\overline{\partial }}\widetilde{\mu }+a\,\cosh {(\sqrt{2}\widetilde{\mu })}\right) +\left( {1\over 2} \partial \widetilde{\chi }\, {\overline{\partial }}\widetilde{\chi }+a\,\cosh {(\sqrt{2}\widetilde{\chi })}\right) , \end{aligned}$$

(2.24)

$$\begin{aligned}&{\text {where}}\quad \quad \widetilde{\mu }={\mu +\chi \over \sqrt{2}},\quad \quad \widetilde{\chi }={\mu -\chi \over \sqrt{2}}. \end{aligned}$$

(2.25)

We have arrived at a system of two independent fields. Their respective energies are conserved, leading to the second integral of motion in the mechanical setting.

It would be interesting to extend this analysis to higher-dimensional homogeneous spaces, whose Pohlmeyer reductions have been studied extensively, cf. [63,64,65] and references therein.

Comment In the derivation above, we assumed ${\mathrm {sgn}}(a_1)={\mathrm {sgn}}(a_2)$. If, on the contrary, ${\mathrm {sgn}}(a_1)=-{\mathrm {sgn}}(a_2)$, after a shift of $\mu$ the function g is found to be $g(\mu )=\frac{\sinh {\mu }-\sinh {\mu _0}}{\cosh {\mu _0}},\;{\mu \ge \mu _0}.$ This is clearly an unbounded geometry. In the limit $\mu _0\rightarrow 0, \mu =\mu _0 \widetilde{\mu }$, with $\widetilde{\mu }\in [1, \infty )$, one obtains the flat space ${\mathbb {R}}^2$.

2.1 The round sphere: ${\mathcal {M}}_2=S^2$

In the case of a sphere, when $g=g_0:={1\over 2}(1-\mu ^2)$, the equations for $\chi , \mu , \phi$ take the form:

$$\begin{aligned}&\partial {\overline{\partial }}\chi +2\sinh {\chi }=0. \end{aligned}$$

(2.26)

$$\begin{aligned}&\partial {\overline{\partial }}\mu +2\mu \,\cosh {\chi }=0. \end{aligned}$$

(2.27)

$$\begin{aligned}&{\overline{\partial }}(g_0(\mu )\,\partial \phi )+\partial (g_0(\mu )\,{\overline{\partial }}\phi )=0. \end{aligned}$$

(2.28)

Therefore, the only essentially nonlinear equation is the first one, and the remaining two are merely a set of nested linear equations.

Let us now derive the Lax pair of the sinh-Gordon model from the Lax pair of the $\mathbb {CP}^1$-model. The latter arises from the condition of zero curvature of the family of connections

$$\begin{aligned}&A_u={1-u\over 2} K_z dz+{1-u^{-1}\over 2} K_{{\overline{z}}} d{\overline{z}},\quad {\text {where}} \end{aligned}$$

(2.29)

$$\begin{aligned}&K_z=g\begin{pmatrix} 0 &{}\quad 2\,(J_{12})_z \\ 0 &{}\quad 0 \end{pmatrix}g^\dagger ,\quad \quad K_{{\overline{z}}}=-K_z^\dagger =g\begin{pmatrix} 0 &{}\quad 0 \\ 2\,(J_{21})_{{\overline{z}}} &{}\quad 0 \end{pmatrix}g^\dagger .\qquad \end{aligned}$$

(2.30)

Here, $J_{12}={\overline{u}}_1\circ du_2$ and $J_{21}={\overline{u}}_2\circ du_1$ are components of the Maurer–Cartan current $J=g^\dagger dg$, where the matrix $g=(u_1, u_2)$, and we assume ${\mathrm {det}}(g)=1$. Upon a gauge transformation by the group element g, we obtain

$$\begin{aligned} {\mathscr {A}}_u= \begin{pmatrix} (J_{11})_z dz+(J_{11})_{{\overline{z}}} d{\overline{z}} &{}\quad u\, (J_{12})_z dz+(J_{12})_{{\overline{z}}} d{\overline{z}} \\ u^{-1}\, (J_{21})_{{\overline{z}}} d{\overline{z}}+(J_{21})_{z} dz &{}\quad -(J_{11})_z dz-(J_{11})_{{\overline{z}}} d{\overline{z}}. \end{pmatrix} \end{aligned}$$

(2.31)

Pohlmeyer’s condition (2.2) may be formulated as $(J_{12})_z (J_{21})_z={1\over 2}$. We set $(J_{12})_z:={1\over \sqrt{2}}e^y$. Due to our parametrization of $\mathbb {CP}^1\simeq {SU(2)\over U(1)}$, we have the gauge group U(1) acting on $J_{12}$ by phase rotations $J_{12}\rightarrow e^{i \alpha }\,J_{12}$; therefore, we can choose a gauge, in which y is real. Then, $(J_{21})_z={1\over \sqrt{2}}e^{-y}, (J_{12})_{{\overline{z}}}=-((J_{21})_z)^*=-{1\over \sqrt{2}}e^{-y}, (J_{21})_{{\overline{z}}}=-((J_{12})_z)^*=-{1\over \sqrt{2}}e^{y}$. From the e.o.m. $D_{{\overline{z}}}(J_{12})_z=(\partial _{{\overline{z}}}+2(J_{11})_{{\overline{z}}})(J_{12})_z =0$, we find $(J_{11})_{{\overline{z}}}=-{1\over 2} \partial _{{\overline{z}}}y$. The connection takes the form

$$\begin{aligned} {\mathscr {A}}_u=\begin{pmatrix} {1\over 2}\,\partial _z y\, dz- {1\over 2}\,\partial _{{\overline{z}}} y \,d{\overline{z}} &{}\quad {1\over \sqrt{2}}\,u\, e^y dz-{1\over \sqrt{2}}\,e^{-y} d{\overline{z}}\\ -{1\over \sqrt{2}}\,u^{-1}\, e^{y} d{\overline{z}}+{1\over \sqrt{2}}\,e^{-y} dz &{}\quad {1\over 2}\,\partial _{{\overline{z}}} y \,d{\overline{z}}-{1\over 2}\,\partial _z y\, dz. \end{pmatrix} \end{aligned}$$

(2.32)

The zero-curvature equation $dA_u+A_u\wedge A_u=0$ then results in the sinh-Gordon equation $\partial {\overline{\partial }}y+\,{\mathrm {sinh}}(2y)=0$. Setting $y={\chi \over 2}$, we return to (2.26). In Sect. 4.2, we will generalize this construction to the case of complete flag manifolds in arbitrary dimension, arriving at a Toda field theory as the relevant counterpart of the sinh-Gordon model.

3 The deformed model $\mathbb {CP}^{n-1}_\eta$

Before starting this section, we point out that the $\eta$-deformation of the $\mathbb {CP}^{n-1}$-model has been recently considered in the works [44,45,46]. We will comment below on the relation of their results to our discussion.

3.1 $\eta$-deformation

The trigonometric deformation (often called $\eta$-deformation) of the principal chiral model was introduced by Klimčík [19,20,21], and the result was generalized by Delduc–Magro–Vicedo to the case of symmetric spaces in [22]. To describe the latter prescription, first we introduce some notation. Let $g\in G$ be the group element, $J=g^{-1}dg$ the standard Maurer–Cartan current, ${\mathfrak {g}}={\mathfrak {h}}\oplus {\mathfrak {m}}$ the decomposition of the Lie algebra of the group G, and $\Pi _{{\mathfrak {h}}}, \Pi _{{\mathfrak {m}}}$ the projectors on the corresponding subspaces. The $\eta$-deformed model of [22] is formulated as follows:

$$\begin{aligned} {\mathscr {L}}= & {} {\mathrm {Tr}}\left( (J_{{\overline{z}}})_{\mathfrak {m}}\, \frac{1}{1-\eta \,\Pi _{\mathfrak {m}}\,R_g\,\Pi _{\mathfrak {m}}}\,(J_z)_{\mathfrak {m}}\right) , \end{aligned}$$

(3.1)

$$\begin{aligned} R_g= & {} {\mathrm {Ad}}_{g^{-1}}\circ {\mathcal {R}}\circ {\mathrm {Ad}}_g, \end{aligned}$$

(3.2)

where ${\mathcal {R}}\in {\mathrm {End}}({\mathfrak {g}})$ is defined as follows: ${\mathcal {R}}=i\,(\pi _+-\pi _-)$, $\pi _\pm$ being the projections on the upper/lower-triangular matrices. First of all, we get rid of the denominator by introducing auxiliary fields⁴$M_z, M_{{\overline{z}}}=M_z^\dagger \in {\mathfrak {g}}_\mathbb {C}$:

$$\begin{aligned} {\mathscr {L}}={\mathrm {Tr}}\left( (J_{{\overline{z}}})_{\mathfrak {m}}\,M_z\right) +{\mathrm {Tr}}\left( M_{{\overline{z}}}(J_z)_{\mathfrak {m}}\right) + {\mathrm {Tr}}\left( {\mathrm {Ad}}_{g}((M_{{\overline{z}}})_{\mathfrak {m}})\,\left( 1 -\eta \,{\mathcal {R}}\,\right) \,{\mathrm {Ad}}_g((M_z)_{\mathfrak {m}})\right) .\nonumber \\ \end{aligned}$$

(3.3)

Now, we wish to formulate the model in terms of the homogeneous coordinates $U_i$, rather than in terms of the unitary group element g. The relation between the two is as follows. Introduce the ‘pseudo-metric’ $\Lambda ={\mathrm {Diag}}(1, -1, \ldots , -1)$ and the group element

$$\begin{aligned} G=g\Lambda g^\dagger ,\quad \quad (G^\dagger =G, \quad G^2=\mathbbm {1}). \end{aligned}$$

(3.4)

The virtue of G is that it is gauge-invariant w.r.t. the gauge group $H=U(1)\times U(n-1)$ (the stabilizer of the quotient space $\mathbb {CP}^{n-1}=\frac{U(n)}{U(1)\times U(n-1)}$). Such gauge-invariant parametrizations were first considered in the context of $\sigma$-models in [8]. In fact, the map $g\rightarrow G$ is an explicit form of Cartan’s embedding $\mathbb {CP}^{n-1}\hookrightarrow U(n)$, which can be written out in the homogeneous coordinates, as desired:

$$\begin{aligned} G=\mathbbm {1}-2\,\frac{U\otimes {\overline{U}}}{\Vert U\Vert ^2}. \end{aligned}$$

(3.5)

It follows from definition (3.4) that

$$\begin{aligned} {\mathcal {J}}:=G^\dagger dG=-\,g\,\left( g^\dagger dg-\Lambda g^\dagger dg \Lambda \right) \,g^\dagger =-2\,g\,J_{{\mathfrak {m}}}\,g^\dagger . \end{aligned}$$

(3.6)

Since $\Pi _{{\mathfrak {m}}}=\frac{1-{\mathrm {Ad}}_\Lambda }{2}$, we can write $(M_z)_{\mathfrak {m}}={1\over 2}\left( M_z-\Lambda M_z \Lambda \right)$. If we now make a field redefinition $M_z \rightarrow g^\dagger M_z g$, we can recast the Lagrangian in the form

$$\begin{aligned} {\mathscr {L}}= & {} -{1\over 2}{\mathrm {Tr}}\left( ({\mathcal {J}}_{{\overline{z}}} )_{\mathfrak {m}}\,{\widetilde{M}}_z\right) -{1\over 2}{\mathrm {Tr}} \left( {\widetilde{M}}_{{\overline{z}}}({\mathcal {J}}_z)_{\mathfrak {m}} \right) + {\mathrm {Tr}}\left( ({\widetilde{M}}_{{\overline{z}}})\,\left( 1 -\eta \,{\mathcal {R}}\,\right) \,({\widetilde{M}}_z)\right) ,\nonumber \\&{\text {where}}\quad \quad {\widetilde{M}}_z={1\over 2}\left( M_z-G M_z G\right) . \end{aligned}$$

(3.7)

The last line contains a projector, which projects on matrices M satisfying $M+G M G=0$. Such matrices can be described as follows:

Lemma 1

A matrix M satisfying $M+G M G=0$ can be parametrized as follows:

$$\begin{aligned} M=U\otimes {\overline{W}}+V\otimes {\overline{U}}\,, \end{aligned}$$

(3.8)

where ${\overline{W}}\circ U={\overline{U}}\circ V=0$, i.e., V, W are two vectors orthogonal to U.

Proof

We write out the equation explicitly:

$$\begin{aligned} M+G M G=2M+4 \,\frac{U\otimes {\overline{U}}\,({\overline{U}} M U)}{\Vert U\Vert ^4}-2\,\frac{U\otimes {\overline{U}}M}{\Vert U\Vert ^2}-2\,\frac{MU\otimes {\overline{U}}}{\Vert U\Vert ^2}=0.\qquad \end{aligned}$$

(3.9)

Multiplying by ${\overline{U}}$, one finds ${\overline{U}} M U=0$; therefore, $M=\frac{U\otimes {\overline{U}}M}{\Vert U\Vert ^2}+\frac{MU\otimes {\overline{U}}}{\Vert U\Vert ^2}$. Denoting $V=\frac{MU}{\Vert U\Vert ^2}$ and ${\overline{W}}=\frac{{\overline{U}}M}{\Vert U\Vert ^2}$, we bring M to the desired form. The vectors V and W are orthogonal to U due to ${\overline{U}} M U=0$. Conversely, a matrix of form (3.8) satisfies $M+G M G=0$. $\square$

Next, we need to substitute M from (3.8) in place of ${\widetilde{M}}_z$ and $M^\dagger$ in place of ${\widetilde{M}}_{{\overline{z}}}$ accordingly. To this end, it is useful to write an explicit expression for the current ${\mathcal {J}}$:

$$\begin{aligned} {1\over 2}{\mathcal {J}}={1\over 2}G^\dagger dG=\frac{U\otimes D{\overline{U}}-DU\otimes {\overline{U}}}{\Vert U\Vert ^2},\quad \quad DU=dU-\frac{{\overline{U}}\circ dU}{\Vert U\Vert ^2}\,U.\qquad \end{aligned}$$

(3.10)

Besides, we introduce the constraints ${\overline{W}}\circ U=0$ and ${\overline{U}}\circ V=0$ using the complex Lagrange multipliers ${\mathcal {B}}$ and ${\mathcal {C}}$:

$$\begin{aligned} {\mathscr {L}}= & {} \left( {\overline{U}}({\mathcal {D}}_{{\overline{z}}}V)\right) +\left( {\overline{U}} ({\mathcal {D}}_{z}W)\right) -\left( ({\mathcal {D}}_{{\overline{z}}} {\overline{W}})U\right) -\left( ({\mathcal {D}}_{z}{\overline{V}})U\right) \\&+ {\mathrm {Tr}}\left( W\otimes {\overline{U}} \,\rho (U\otimes {\overline{W}})\right) +{\mathrm {Tr}}\left( U\otimes {\overline{V}} \,\rho (V\otimes {\overline{U}})\right) \nonumber \\&+ {\mathrm {Tr}}\left( U\otimes {\overline{V}} \,\rho (U\otimes {\overline{W}})\right) +{\mathrm {Tr}}\left( W\otimes {\overline{U}} \,\rho (V\otimes {\overline{U}})\right) ,\nonumber \\&{\text {where}}\quad \quad {\mathcal {D}}_{z}W=\partial _z W-i \,{\mathcal {B}}\,W,\quad \quad {\mathcal {D}}_{{\overline{z}}}V=\partial _{{\overline{z}}} V-i\, {\mathcal {C}}\,V,\nonumber \end{aligned}$$

(3.11)

where we have introduced the notation $\rho =1-\eta \,{\mathcal {R}}$. As elaborated in [46], this is really an example of generalized Kähler geometry. In particular, the quadratic form in the last two lines of (3.11) encodes the generalized Kähler metric [66].

The matrix $\rho$ is closely related to the (trigonometric) classical r-matrix. We recall a few facts about the latter. In the analysis of the Yang–Baxter equation (see App. A), one usually assumes that the r-matrix takes values in ${\mathfrak {g}}\otimes {\mathfrak {g}}$; however, for the purposes of this paper it is more useful to think of it as taking values in ${\mathrm {End}}({\mathfrak {g}})$, the two definitions being related by raising/lowering an index using the Killing metric on ${\mathfrak {g}}$. The r-matrix then has the form (we assume ${\mathfrak {g}}\simeq \mathfrak {su}_n$)

$$\begin{aligned} r_s= & {} \alpha _s\,\pi _++\beta _s \,\pi _-+\gamma _s\,\pi _0, \end{aligned}$$

(3.12)

$$\begin{aligned} \alpha _s= & {} \frac{1}{1-s},\quad \quad \beta _s=\frac{s}{1-s},\quad \quad \gamma _s={1\over 2}\,\frac{1+s}{1-s}, \end{aligned}$$

(3.13)

where $\pi _\pm$ are projections on the upper-/lower-triangular matrices and $\pi _0$ is the projection on the diagonal. The rational limit is achieved by setting $s=e^{-v}$ and taking the limit $v\rightarrow 0$, in which case $r_s\rightarrow \frac{\mathbbm {1}}{v}$. Now, the relation of $r_s$ to $\rho$ is $r_s={\rho \over 2i\eta }$, if one assumes the following relation between the parameters:

$$\begin{aligned} s=\frac{1-i\,\eta }{1+i\,\eta }. \end{aligned}$$

(3.14)

In fact, this suggests introducing the notation $\eta =\tan {({t_n\over 2})}$, in which case $s=e^{-i \,t_n}$. We will be using this parametrization later on.

Incidentally, formula (3.14) is the same one that relates the parameter $\eta$ of the Yang–Baxter $\eta$-deformation to the parameter $\lambda =s$ of the so-called $\lambda$-deformation [67, 68] via Poisson-Lie T-duality⁵ [69,70,71]. The RG-flow of the $\lambda$-parameter in the case of deformed symmetric space models is particularly simple: ${d\lambda \over d\tau }\sim n\,\lambda$ [72] ($\tau$ being the RG-time), which coincides with the result that we will obtain below, see Sect. 3.4, in our study of the $\eta$-deformation ($t_n=n \tau$, so that $s=e^{-i n\tau }$). This can be explained by the fact that RG-flow commutes with Poisson-Lie T-duality [73, 74].

We return to the Lagrangian (3.11). There are several ways to proceed from this starting point. One can integrate out the fields V, W (the quadratic part is a Hermitian form in the variables $(V, {\overline{W}}), ({\overline{V}}, W)$) and get a deformed $\mathbb {CP}^{n-1}_\eta$ Lagrangian that depends on the U-fields. The calculation along these lines seems rather formidable and leads to a generalized Kähler manifold [46]. As it has already been observed in [44], a simpler answer can be obtained if one performs T-duality in all the angular directions of the deformed space. The reason is that the B-field of the above model has the form $B=\sum \,b_i\wedge d\phi _i$, where $b_i$ are some one-forms that do not depend on $\phi _j$. In this case, according to the Buscher rules [75] (for a review of T-duality see also [76]), T-duality along all the directions $\phi _i$ eliminates the B-field altogether. We will also follow this path, but first we recall how T-duality works for Kähler manifolds.

3.2 T-duality for toric Kähler manifolds

Although the $\eta$-deformed manifold $\mathbb {CP}^{n-1}_\eta$ is not Kähler in general (unless $n=2$), let us first recall that, in the Kähler setup, T-duality may be implemented by performing a Legendre transform on the Kähler potential. This is especially easy to see in the case of a toric variety (see [77, 78] for background on toric Kähler manifolds), and when T-duality is performed on all angles simultaneously. Indeed, suppose we have a Kähler manifold of complex dimension n, with complex coordinates $W_1, \ldots , W_n$. Assume that the torus acts by shifting $W_k \rightarrow W_k +i\, \delta \phi _k$, i.e., the imaginary parts of $W_k$ are the angles. On a toric manifold, the Kähler potential may be then assumed to be of the form

(3.15)

The line element is

$$\begin{aligned} ds^2=\sum \limits _{j,k=1}^n\,\left( {1\over 4}\frac{\partial ^2 {\mathcal {K}} }{\partial t_j \partial t_k}\,dt_j\,dt_k+\frac{\partial ^2 {\mathcal {K}} }{\partial t_j \partial t_k}\,d\phi _j\,d\phi _k\right) . \end{aligned}$$

(3.16)

It is also useful to define the moment map variables $\mu _k={\partial {\mathcal {K}}\over \partial t_k}$, and the dual potential $H(\mu _1, \ldots , \mu _n)$, also known as the symplectic potential. It is related to ${\mathcal {K}}$ by a Legendre transform: $H(\mu _1, \ldots , \mu _n)=\sum \nolimits _{j=1}^n\,\mu _j\,t_j-{\mathcal {K}}(t_1, \ldots , t_n)$. An elementary property of the Legendre transform is that the Hessian of H is inverse to the Hessian of K, i.e., suppressing the matrix indices we may write ${\partial ^2 H\over \partial \mu ^2}=({\partial ^2 K\over \partial t^2})^{-1}$. In terms of these new variables, the metric takes the form

$$\begin{aligned} ds^2=\sum \limits _{j,k=1}^n\,\left( {1\over 4}\frac{\partial ^2 H }{\partial \mu _j \partial \mu _k}\,d\mu _j\,d\mu _k+\left( \frac{\partial ^2 H }{\partial \mu ^2}\right) ^{-1}_{jk}\,d\phi _j\,d\phi _k\right) . \end{aligned}$$

(3.17)

We note in passing that, for $n=1$, this gives essentially formula (2.1) for the metric of the two-dimensional space that we studied in Sect. 2. One of the virtues of the symplectic potential H is that its domain of definition is of geometric significance—it is the moment polytope of the manifold.

If we now perform T-duality on all angles $\phi _k$ simultaneously, this will not generate any B-field, but the matrix in the second term of (3.17) will be inverted. In this case, the metric takes form (3.16), but with the replacement $K\leftrightarrow H, t_k \leftrightarrow \mu _k$. In other words, T-duality works by interchanging the Kähler potential with its Legendre-dual, the symplectic potential.

From the point of view of supersymmetric theory, Kähler target spaces correspond to ${\mathcal {N}}=(2, 2)$ worldsheet supersymmetry. The complex coordinates correspond to chiral superfields, and partial T-dualities replace chiral superfields by twisted chiral superfields [79, 80]. In general, the presence of both chiral and twisted chiral superfields leads to a non-topological B-field. However, if we T-dualize all variables, all chiral superfields are replaced by twisted chiral superfields, which is effectively the same as having all chiral superfields and leads again to Kähler geometry, described by the dual potential.

This leads us then to the following curious question. We start with the $\eta$-deformed geometry $\mathbb {CP}^{n-1}_\eta$, which is a toric manifold and has, in general, a non-topological B-field. Next, we T-dualize all angles and get rid of the B-field completely. Since we expect ${\mathcal {N}}=(2, 2)$ supersymmetry to be preserved, the resulting manifold should be Kähler, again with n commuting isometries. If its Kähler potential was of form (3.15), the metric would have form (3.16)–(3.17), but in this case the inverse T-duality would not generate any B-field and therefore would not lead us to the original geometry. So, how is this apparent puzzle resolved? In Sect. 3.3, we will analyze the T-dual Kähler geometry in detail, but the ultimate answer will be that, due to the fact that this manifold is no longer simply connected, the moment map variables $\mu _k$ are not well defined (only the one-forms $d\mu _k$ are). As a result, the T-dual metric cannot really be brought to form (3.16)–(3.17). Before passing over to this derivation, we briefly recall the symplectic geometry of the $\mathbb {CP}^{n-1}$ space. This will be useful for the following sections, since essentially the same variables may be used for the description of the deformed geometry.

3.2.1 The undeformed $\mathbb {CP}^{n-1}$ geometry and its T-dual

The complex projective space is defined as the set of equivalence classes of n-tuples of complex numbers $(Q_1, \ldots , Q_n )\in \mathbb {C}^n{\setminus }\{0\}$ w.r.t. to the $\mathbb {C}^\times$-action $Q_i \rightarrow \lambda \,Q_i$. One may also describe it using a symplectic (Kähler) quotient of $\mathbb {C}^n$ w.r.t. a U(1)-action that preserves the standard symplectic form. This leads to the Kähler potential that in homogeneous coordinates takes the form

$$\begin{aligned} {\mathcal {K}} =\log {\left( \sum \limits _{j=1}^n |Q_j|^2\right) }. \end{aligned}$$

(3.18)

In the previous section, we assumed an additive, rather than multiplicative, action of the torus; therefore, we set $Q_j=e^{W_j}$, so that ${\mathcal {K}}=\log {\left( \sum \nolimits _{j=1}^n e^{{\widetilde{t}}_j}\right) }$. We have marked the t-variables with a tilde, since ultimately we will be interested in the T-dual Kähler potential, and we reserve the unmarked t-variables for that case. The moment map variables are then $\mu _j={\partial {\mathcal {K}}\over \partial {\widetilde{t}}_j}=\frac{e^{{\widetilde{t}}_j}}{\sum \nolimits _{j=1}^n e^{{\widetilde{t}}_j}}$. The symplectic potential has the form

$$\begin{aligned} H=\sum \limits _{j=1}^n\,\mu _j\,\log {\mu _j},\quad \quad {\text {where}}\quad \mu _j\ge 0 \quad \text {and}\quad \sum \limits _{j=1}^n\,\mu _j=1. \end{aligned}$$

(3.19)

This expression has a particularly simple interpretation in terms of the Kähler quotient. Indeed, $\sum \nolimits _{j=1}^n\,\mu _j\,\log {\mu _j}$ is the symplectic potential of $\mathbb {C}^n$, and the constraint $\sum \nolimits _{j=1}^n\,\mu _j=1$ is the restriction of the moment map, corresponding to the diagonal U(1)-action. The constraints in (3.19) define the moment polytope of $\mathbb {CP}^{n-1}$, which is an $(n-1)$-dimensional simplex.

Let us now derive, again in the undeformed case, the Kähler potential of the T-dual metric. As discussed earlier, it is equal to the symplectic potential H of the original metric. Solving the moment map constraint by setting $\mu _k=t_k-t_{k-1}$, where $t_n-t_0=1$ ($t_0$ and $t_n$ are parameters), and using (3.19), we find

$$\begin{aligned} {\mathcal {K}}^{\vee }=\sum \limits _{j=1}^n\,(t_j-t_{j-1})\, \log {(t_j-t_{j-1})},\quad \quad {\text {where}}\quad t_j\ge t_{j-1}. \end{aligned}$$

(3.20)

We will be using this formula as a test of our result for the deformed metric in the limit $\eta \rightarrow 0$.

3.2.2 The ‘sausage’ and its T-dual

Let us consider in detail the case $n=2$, i.e. the deformation of the sphere $\mathbb {CP}^1\simeq S^2$ that we discussed in Sec. 2. We start from the metric written in the ‘stereographic’ complex coordinates

which is another form of the sausage metric that may be obtained from (2.1), (2.22) by passing to conformal coordinates and setting $s=e^{-\mu _0}$. To bring the metric to the form that was originally found in [42], we parametrize $W=e^{{\widetilde{t}\over 2}+i \phi }$, in which case ($s^{-1}=e^{2\tau }$)

$$\begin{aligned} ds^2=\sinh {(2\tau )}\,\frac{{1\over 4}\,d\widetilde{t}^2+d\phi ^2}{\cosh (\widetilde{t})+\cosh {(2\tau )}}\,,\quad \quad \widetilde{t}\in (-\infty , \infty ), \;\phi \in [0, 2\pi )\,. \end{aligned}$$

(3.22)

Interestingly, apart from the U(1) isometry $\phi \rightarrow \phi +\mathrm {const.}$, there are two $\mathbb {Z}_2$-isometries: $\phi \rightarrow -\phi$ and $\widetilde{t}\rightarrow -\widetilde{t}$. From the point of view of the complex coordinate W, they may be combined to the following two isometries: $W\rightarrow \overline{W}$ and $W\rightarrow {1\over W}$.

So far we have encountered several forms of the sausage metric. It is particularly instructive to compare the moment-map form (2.22) and the conformally flat form (3.22). If one performs a T-duality on the $\phi$-angle of the metric (2.22) and makes a change of variables $\mu _0= 2\tau +i\,\pi ,$ $\mu = \widetilde{t}$, one arrives at the metric (3.22). Therefore T-duality is effectively performed in this case by a simple analytic continuation of the parameter. Of course this is a formal manipulation, since the range of coordinates also needs to be changed. For example, the range of the moment map of the T-dual metric is in fact infinite, and the metric has singularities at infinite values of this variable.

Let us see, how this analytic continuation works at the level of the Kähler potential, which can be read off from the metric (3.22) by comparing to the general toric Kähler metric (3.16). It follows that $\mathcal {K}''(\widetilde{t})=\frac{\sinh {(2\tau )}}{\cosh (\widetilde{t})+\cosh {(2\tau )}}$, so that⁶

T-duality simply flips the sign, $s\rightarrow -s$. After this sign flip, as can be seen from (3.21), the range of the coordinates is $|W|^2\in [s, {1\over s}]$. Since T-duality is implemented by a Legendre transform at the level of the potential, we come to the following statement:

Lemma 2

The Legendre transform maps $\mathcal {K}_s(\widetilde{t})=\mathrm {Li}_2(-s e^{\widetilde{t}})-\mathrm {Li}_2(-s^{-1} e^{\widetilde{t}})$ to $\mathcal {K}_{-s}(t)$.

Proof

The proof is an application of the five-term identity for the dilogarithm. It is easier to work with Rogers’ dilogarithm L(x) defined as $L(x)=\mathrm {Li}_2(x)+{1\over 2}\log {x}\,\log {(1-x)}$ for $0<x<1$. A suitable analytic continuation to the whole real axis is described in [81]. We start from the so-called Abel identity [81] $L({1-a\over 1-b})+L({b\over a})=L({1-a\over 1-b}\cdot {b\over a})+L(1-a)+L(b)$. Since $L(a)+L(1-a)=\mathrm {const.}$, we find $L({1-a\over 1-b})+L({b\over a})\simeq L({1-a\over 1-b}\cdot {b\over a})+L(b)-L(a)$. Next we calculate the moment map $\mu -\log {s}={d \mathcal {K}_s(\widetilde{t})\over d\widetilde{t}}=\log {({1+s^{-1}e^{\widetilde{t}}\over 1+s e^{\widetilde{t}}})}$ and substitute $a=-s^{-1} e^{\widetilde{t}}, b=-s e^{\widetilde{t}}$ in the identity to find $L(s^{-1}\,e^\mu )+L(s^2)\simeq L(s\, e^\mu )+L(-s e^{\widetilde{t}})-L(-s^{-1} e^{\widetilde{t}})$. Returning to the dilogarithm $\mathrm {Li}_2$, we may rewrite this, up to inessential terms that are linear in either $\widetilde{t}$ or $\mu$: $\widetilde{t}\mu -\mathcal {K}_s(\widetilde{t})\simeq \mathcal {K}_{-s}(\mu )$, which is the definition of the Legendre transform. Finally, we recall that the moment map variable $\mu$ on the original manifold is relabelled as t, when viewed as a coordinate on the T-dual manifold. $\square$

Let us record for the future, that in the metric (3.21) the limit $s\rightarrow 1$ (up to a vanishing factor) corresponds to the round metric on $S^2$, whereas the limit $s\rightarrow 0$ corresponds to the flat metric $\frac{|dW|^2}{|W|^2}$ on a cylinder $\mathbb {R}\times S^1$.

The metric (3.21) has another important regime, where it is still well-defined, namely $s\in \mathbb {C}$, $|s|=1$. We denote $s=e^{2i\tau }$. In this case, when rescaled by a factor of i, the metric takes the form $ds^2=\sin {(2\tau )}\,\frac{{1\over 4}\,d\widetilde{t}^2+d\phi ^2}{\cosh (\widetilde{t})+\cos {(2\tau )}}$. If we now perform T-duality and bring the dual metric to the conformal form, we obtain $(ds^2)^{\vee }=\sin {(2\tau )}\,\frac{{1\over 4}\,dt^2+d\phi ^2}{\cos (t)-\cos {(2\tau )}}$, and the range of the new variable t is $t\in [-2\tau , 2\tau ]$. The dual Kähler potential is, in this regime,

$$\begin{aligned} \mathcal {K}^{\vee }=i\,(\mathrm {Li}_2(e^{i(t+2\tau )})-\mathrm {Li}_2 (e^{i(t-2\tau )})),\quad \quad \quad s=e^{2i\tau }\,. \end{aligned}$$

(3.24)

Strictly speaking, this expression has a non-zero imaginary part. The imaginary part is, however, an elementary function [82], and moreover it is linear in t, therefore not contributing to the metric. We note that in our generalizations to the case of $\mathbb {CP}^{n-1}_\eta$ we will mostly encounter formulas similar to (3.24), i.e. with the dilogarithm evaluated on the unit circle. Indeed, this is the Kähler potential for the metric, T-dual to the unitary deformation of the $\mathbb {CP}^{n-1}$ model (that is, with $\eta$ real, see (3.14)).

3.3 The T-dual Kähler geometry for all n

We pass to the derivation of the T-dual model for arbitrary n. Let $\mathcal {R}_{jk}=1$ for $j<k$, $\mathcal {R}_{jk}=-1$ for $j>k$ and $\mathcal {R}_jj=0$ (these are the coefficients of the operator $\mathcal {R}$ defined earlier). The metric can then be described as follows:

Proposition 2

Define the matrix $N_{jk}:=x_j\,(i\,{\mathcal {R}}_{jk})$ ($j, k =1, \ldots , n$). The metric, T-dual to the $\mathbb {CP}^{n-1}_\eta$ geometry, has the form:

$$\begin{aligned} ds^2= & {} \sum \limits _{j=1}^n\,\frac{d \psi _j^2+\left( dx_j -\eta \,M_j\right) ^2}{2 x_j}, \end{aligned}$$

(3.25)

$$\begin{aligned} M_j= & {} \sum \limits _{k=1}^n\,\left( N_{jk}-\sum \limits _{i=1}^n \,N_{ik}\,\delta _{jk}\right) \,d\psi _k,\end{aligned}$$

(3.26)

$$\begin{aligned}&{\text {where}}\quad \quad x_j\ge 0,\quad \quad \sum \limits _{j=1}^n\,x_j=1,\quad \quad \sum \limits _{j=1}^n \,\psi _j=0. \end{aligned}$$

(3.27)

Comment In the limit $\eta \rightarrow 0$, the variables $x_j$ become the moment map variables of the original $\mathbb {CP}^{n-1}$ manifold, albeit viewed as coordinates on the T-dual $(\mathbb {CP}^{n-1})^\vee$ manifold. This explains the constraints $x_j\ge 0, \;\sum \nolimits _j\,x_j=1$ as originating from the analogous constraints for $\mathbb {CP}^{n-1}$, see (3.19). Note that these are not the same as the moment map variables of the dual $(\mathbb {CP}^{n-1})^\vee$, which coincide with the ${\widetilde{t}}$-variables of the original $\mathbb {CP}^{n-1}$. In an attempt to avoid this confusion, we call our variables $x_j$, rather than $\mu _j$. The relation between x- and t-variables on $(\mathbb {CP}^{n-1}_\eta )^\vee$ follows from the proof of Proposition 3 below.

Proof

We start from the Lagrangian (3.11), parametrizing the variables as $U_j=e^{Y_j}=x_j^{1/2}e^{i\,\phi _j}$. We will also make a change of variables $V_j\rightarrow e^{-{\overline{Y}}_j}\,V_j,\;\;W_j\rightarrow e^{-{\overline{Y}}_j}\,W_j$. The Lagrangian then takes the form

$$\begin{aligned} {\mathscr {L}}= & {} {\overline{W}}_k{\overline{\partial }}Y_k+{\overline{V}}_k\partial Y_k-W_k\partial {\overline{Y}}_k-V_k{\overline{\partial }}{\overline{Y}}_k \end{aligned}$$

(3.28)

$$\begin{aligned}&+\sum \limits _{i, \,j}\,\frac{x_j}{x_i}\,(W_i\,{\overline{W}}_i\,\rho _{ji} +V_i\,{\overline{V}}_i\,\rho _{ij})+\sum \limits _{i, \,j}\,\rho _{ji} (V_jW_i+{\overline{V}}_j{\overline{W}}_i),\end{aligned}$$

(3.29)

$$\begin{aligned}&\text {and}\quad \quad \sum \limits _{k} W_k=\sum \limits _{k} V_k=0. \end{aligned}$$

(3.30)

Note that the constraints are linear in the new variables. The constants $\rho _{ij}$ are defined as follows: $\rho (A)=B, B_{ij}=\rho _{ij} A_{ij}$, i.e., $\rho _{pq}=1-i\eta \epsilon (q-p)$ ($\epsilon$ is the skew-symmetric step function). The Lagrangian is invariant under shifts of the angular variables, $\phi _j\rightarrow \phi _j+\alpha _j$. The e.o.m. for $\phi _j$ is simply ${\overline{\partial }}(V_k+{\overline{W}}_k)+\partial ({\overline{V}}_k+W_k)=0$. According to the standard lore of T-duality, we ‘solve’ it by setting

$$\begin{aligned} V_k+{\overline{W}}_k=i\,\partial \psi _k,\quad \quad {\overline{V}}_k+W_k=-i\,{\overline{\partial }}\psi _k, \end{aligned}$$

(3.31)

where $\psi _k$ are the new (real) variables that are dual to the $\phi$-angles. Due to the constraints (3.30) one also has $\sum \limits _{k}\,\psi _k=0$, up to an inessential overall shift. It is now clear, where the main simplification comes from—we have gotten rid of half of the variables (V, W) that we needed to ‘integrate over.’ Leaving just the V-variables, we obtain the Lagrangian

$$\begin{aligned} {\mathscr {L}}= & {} i\,\sum \limits _k\,\frac{\partial \psi _k {\overline{\partial }}x_k+{\overline{\partial }}\psi _k \partial x_k}{2\,x_k}+2\,\sum \,\frac{x_j}{x_i}\,|V_i|^2+\sum \,\rho _{ji}\,\frac{x_j}{x_i}\,\partial \psi _i {\overline{\partial }}\psi _i\nonumber \\&+ \sum \limits _k\,V_k\,{1\over x_k}\,\left( -{\overline{\partial }}x_k+i\,\left( \sum \limits _j\,x_j\,\rho _{jk}\right) \,{\overline{\partial }}\psi _k-i\,x_k\,\sum \limits _j\,\rho _{kj}\,{\overline{\partial }}\psi _j+{\mathcal {C}}\,x_k\right) \nonumber \\&+ \sum \limits _k\,{\overline{V}}_k\,{1\over x_k}\,\left( \partial x_k-i\,\left( \sum \limits _j\,x_j\,\rho _{jk}\right) \,\partial \psi _k+i\,x_k\,\sum \limits _j\,\rho _{kj}\,\partial \psi _j-\overline{{\mathcal {C}}}\,x_k\right) .\nonumber \\ \end{aligned}$$

(3.32)

In this derivation, we have used the property $\rho _{ij}+\rho _{ji}=2$. Besides, ${\mathcal {C}}$ is the Lagrange multiplier imposing $\sum \limits _k\,V_k=0$. Upon introducing the new variables $P_i=\sum \limits _j\,\rho _{ji}\,x_j$ and $R:=\sum \limits _j\,x_j$, we eliminate $V_k$:

$$\begin{aligned} {\mathscr {L}}= & {} i\,\sum \limits _k\,\frac{\partial \psi _k {\overline{\partial }}x_k+{\overline{\partial }}\psi _k \partial x_k}{2\,x_k}+\sum \limits _i\,{P_i\over x_i}\,\partial \psi _i {\overline{\partial }}\psi _i\nonumber \\&-{1\over 2 R}\,\sum \limits _k\,{1\over x_k}\, \left( - {\overline{\partial }}x_k+i\,P_k\,{\overline{\partial }}\psi _k-i\,x_k\,\sum \limits _j\,\rho _{kj}\,{\overline{\partial }}\psi _j+{\mathcal {C}}\,x_k\right) \nonumber \\&\left( \partial x_k-i\,P_k\,\partial \psi _k+i\,x_k\,\sum \limits _j\,\rho _{kj}\,\partial \psi _j-\overline{{\mathcal {C}}}\,x_k\right) . \end{aligned}$$

(3.33)

Differentiating w.r.t. $\overline{{\mathcal {C}}}$, we find ${\mathcal {C}}={\overline{\partial }}\log {R}$. In fact, using the projective freedom it is convenient to set $R=\sum \limits _j x_j=1$, and therefore, ${\mathcal {C}}=\overline{{\mathcal {C}}}=0$. In this case,

$$\begin{aligned} {\mathscr {L}}= & {} i\,\sum \limits _k\,\frac{\partial \psi _k {\overline{\partial }}x_k+{\overline{\partial }}\psi _k \partial x_k}{2\,x_k}+\sum \limits _i\,{P_i\over x_i}\,\partial \psi _i {\overline{\partial }}\psi _i\nonumber \\&-{1\over 2 }\,\sum \limits _k\,{1\over x_k}\, \left( - {\overline{\partial }}x_k+i\,P_k\,{\overline{\partial }}\psi _k-i\,x_k\,\sum \limits _j\,\rho _{kj}\,{\overline{\partial }}\psi _j\right) \nonumber \\&\left( \, \partial x_k-i\,P_k\,\partial \psi _k+i\,x_k\,\sum \limits _j\,\rho _{kj}\,\partial \psi _j\right) . \end{aligned}$$

(3.34)

We can read off the metric of the target space ($P_k=1+i\,\eta \,\tau _k$):

$$\begin{aligned} ds^2= & {} i\,\sum \limits _k\,{d \psi _k d x_k\over x_k}+\sum \limits _k\,{ 1+i\,\eta \,\tau _k\over x_k}\,d \psi _k^2\nonumber \\&+{1\over 2 }\,\sum \,{1\over x_k} \,(dx_k-i\,d\psi _k-\eta \,M_k)^2 \end{aligned}$$

(3.35)

$$\begin{aligned} M_k= & {} -\tau _k\,d\psi _k-x_k\,\sum \limits _j\,(i\,{\mathcal {R}}_{kj})\,d\psi _j. \end{aligned}$$

(3.36)

A direct simplification (getting rid of the fictitious imaginary part) leads to the expression declared in the Proposition. $\square$

Comment For some purposes, it is useful to restore the projective invariance (i.e., $x\rightarrow \lambda \,x$) in the metric. Namely, we wish to drop the gauge $\sum \nolimits _j\,x_j=1$ and work in a gauge-invariant way. In that case, the metric may be written as follows:

$$\begin{aligned} ds^2=\sum \limits _{j=1}^n\,\left( \frac{R\,d \psi _j^2}{2 x_j} +\frac{\left( dx_j-x_j\,d\log {R}-\eta \,M_j\right) ^2}{2\,R\,x_j}\right) , \quad \quad R=\sum \limits _k\,x_k. \end{aligned}$$

(3.37)

This has the local rescaling invariance $x_j \rightarrow \lambda x_j$, with $\lambda$ an arbitrary function.

We come to the description of the Kähler structure of the metric (we drop the superscript $\vee$ in $\mathcal {K}^\vee$ in what follows, since this is the only Kähler potential we will be dealing with):

Proposition 3

The metric defined in (3.25)–(3.27) is Kähler. In the complex coordinates $Z_j, j=1, \ldots , n-1$, the Kähler potential may be written as ($\eta >0$, $t_0$ and $t_n$ are parameters)

$$\begin{aligned} {\mathcal {K}}= & {} \sum \limits _{j=2}^{n-1}\,i\,\eta (Z_j {\overline{Z}}_{j-1} -{\overline{Z}}_j Z_{j-1})+{1\over 2\eta }\,\sum \limits _{j=1}^n\,P \left( 2\eta (t_j-t_{j-1})\right) ,\\&{\text {where}}\quad \quad P(t)=i\left( {\mathrm {Li}}_2 (e^{i t})+{t(2\pi -t)\over 4}\right) ,\quad \quad \text {and} \quad \quad t_j:=Z_j+{\overline{Z}}_j.\nonumber \end{aligned}$$

(3.38)

$$\begin{aligned}&\text {Coordinate range:} \; -\pi \le 2\eta \,t_0\le 2\eta t_1 \le \cdots \le 2\eta t_{n-1} \le 2\eta t_n=-2\eta t_0 \le \pi .\nonumber \\ \end{aligned}$$

(3.39)

Comment Before passing to the proof, we perform an elementary check by taking the limit $\eta \rightarrow 0$. Note that $P''(t)={1\over 2}\mathrm {ctg}({t\over 2})$, so that in the limit $\eta \rightarrow 0$ the asymptotic behavior is $P(2\eta t)\rightarrow 2\eta t\log {(t)}$, up to linear terms. The potential then coincides with potential (3.20) of the undeformed $(\mathbb {CP}^{n-1})^{\vee }$ model. In the case $n=2$ the potential (3.38) can be matched with (3.24) by using an elementary dilogarithm identity.

Proof

Let us write the metric in the form $ds^2=\sum \nolimits _{j=1}^n\,\frac{\theta _j \overline{\theta }_j}{2 x_j}$, where $\theta _j=d \psi _j+i\,(dx_j-\eta \,M_j)$. We will denote $M_j:=\sum \nolimits _k\,M_{jk}\,d\psi _k$. Due to (3.27), the $\theta$-forms are subject to the condition $\sum \nolimits _{j=1}^n\,\theta _j=0$.

Now, $\theta _j$ may be taken as a basis of (0, 1)-forms of an integrable complex structure. To see this, we need to check that $\Omega ^*({\mathcal {M}})(\theta _1, \ldots , \theta _n)$ is a differential ideal in the ring of forms $\Omega ^*({\mathcal {M}})$. In other words, one needs to show that the (2, 0) part of $d\theta _i$ vanishes. We compute $d\theta _j=\eta \,\sum \limits _k\,{\mathcal {R}}_{jk}(dx_j \wedge d\psi _k+dx_k\wedge d\psi _j)$. Using the fact that $d\psi _j={\theta _j+\overline{\theta }_j\over 2}$ and $dx_j={\theta _j-\overline{\theta }_j\over 2i}+{\eta \over 2}\,\sum \limits _s\,M_{js}\,(\theta _s+\overline{\theta }_s)$, after a simple calculation we find that

$$\begin{aligned} (d\theta _j)^{(2, 0)}=-\frac{i\,\eta ^2}{4}\,\sum \limits _{k, s}\,x_s\,\left( {\mathcal {R}}_{js}{\mathcal {R}}_{sk}+{\mathcal {R}}_{jk} {\mathcal {R}}_{sj}-{\mathcal {R}}_{jk}{\mathcal {R}}_{sk} +\delta _{jk}\,\delta _{sk}\right) \,\overline{\theta }_j\wedge \overline{\theta }_k.\nonumber \\ \end{aligned}$$

(3.40)

We have added the term $\delta _{jk}\,\delta _{sk}$, since it does not affect the result due to the wedge product $\overline{\theta }_j\wedge \overline{\theta }_k$, but it ensures that the expression in brackets is identically 1. When $j=k=s$, this is due to the delta-symbols. In all other cases, one can decide, which index takes the largest value, which makes it easy to check that the ${\mathcal {R}}{\mathcal {R}}$-terms add up to unity. As a result, $(d\theta _j)^{(2, 0)}=-\frac{i\,\eta ^2}{4}\,\sum \nolimits _{k}\,\overline{\theta }_j\wedge \overline{\theta }_k=0$.

The fundamental Hermitian form, corresponding to the metric, is

$$\begin{aligned} \Omega= & {} {i\over 2}\sum \limits _{j=1}^n\,\frac{\theta _j \wedge \overline{\theta }_j}{2 x_j} =\sum \limits _{j=1}^n\,\frac{d\psi _j\wedge (dx_j-\eta \,x_j\,\sum \nolimits _k (i\,{\mathcal {R}}_{jk})\,d\psi _k)}{2 x_j} \nonumber \\= & {} \sum \limits _{j=1}^n\,\frac{d\psi _j\wedge dx_j}{2 x_j}-{\eta \over 2}\,\sum \limits _{j,\,k}\, (i\,{\mathcal {R}}_{jk})\,d\psi _j\wedge d\psi _k. \end{aligned}$$

(3.41)

Clearly, it is closed: $d\Omega =0$.

Next, we come to the actual determination of the complex coordinates. In other words, we need to find the integrating multipliers for the set of one-forms $\{\theta _k\}_{k=1 \ldots n}$. We introduce the new coordinates $y_k:=\sum \nolimits _{i=1}^k\,x_i$ and $\chi _k:=\sum \nolimits _{i=1}^k\,\psi _i$, as well as the new one-forms $\Theta _k:=\sum \nolimits _{i=1}^k\,\theta _i$. Note that $y_n=1, \chi _n=0, \Theta _n=0$. Besides, since the $x_k$-variables are non-negative, we find that $y_{k+1}\ge y_k$. It turns out that

$$\begin{aligned} \Theta _k=(1+i\eta \,(1-2y_k))\,d\chi _k+i\,dy_k. \end{aligned}$$

(3.42)

To prove this, we recall that $(i{\mathcal {R}})_{jk}=-1$ for $j<k$ and $(i{\mathcal {R}})_{jk}=1$ for $j>k$. Therefore $\sum \nolimits _m\,(i{\mathcal {R}})_{jm} d\psi _m=-\sum \nolimits _{m\ge j}\,d\psi _m+\sum \nolimits _{m\le j}\,d\psi _m=d\chi _{j-1}+d\chi _j$. Besides, we express ${d\psi _k=d\chi _k-d\chi _{k-1}}$, so that

$$\begin{aligned} \sum \limits _{j=1}^k M_j= & {} \sum \limits _{j=1}^k\,d\chi _j\,\left( x_j+\sum \limits _{m<j} \,x_m-\sum \limits _{m>j}\,x_m\right) \\&+\sum \limits _{j=2}^k\,d\chi _{j-1}\, \left( x_j+\sum \limits _{m>j}\,x_m-\sum \limits _{m<j}\,x_m\right) \\= & {} -\sum \limits _{j=1}^k\,d\chi _j\,(1-2\,y_j)+\sum \limits _{j=2}^k\, d\chi _{j-1}\,(1-2\,y_{j-1})=-d\chi _k\,(1-2\,y_k). \end{aligned}$$

Equality (3.42) then follows. It is convenient to make a shift $\chi _k\rightarrow \chi _k+{1\over 4\eta } \log {\left( 1+\eta ^2\,(1-2 \,y_k)^2\right) }$, in which case we get

$$\begin{aligned} \Theta _k= & {} (1+i\eta \,(1-2 y_k))\,\left( d\chi _k+i\,\frac{dy_k}{1+\eta ^2 \,(1-2 y_k)^2}\right) \nonumber \\= & {} (1-i\tan {(\eta \,t_k)})\,(d\chi _k+{i\over 2}\,dt_k) =\frac{e^{-i\,\eta \,t_k}}{\cos {(\eta \,t_k)}}\,(d\chi _k+{i\over 2}\,dt_k)\nonumber \\:= & {} \frac{i\,e^{-i\,\eta \,t_k}}{\cos {(\eta \,t_k)}}\,dZ_k, \end{aligned}$$

(3.43)

where $\tan {(\eta \,t_k)}=\eta \,(2 y_k-1)$ and we have introduced the complex variable $Z_k:={1\over 2}\,t_k-i\,\chi _k$. Due to the constraint $y_{k+1}\ge y_k$, we get $t_{k+1}\ge t_k$. Since $\theta _j=\Theta _j-\Theta _{j-1}$, the metric has the form

$$\begin{aligned} ds^2=\sum \limits _{j=1}^n\,\eta \,\frac{\Vert \Theta _j-\Theta _{j-1}\Vert ^2}{\tan {(\eta \,t_j)}-\tan {(\eta \,t_{j-1})}}, \end{aligned}$$

(3.44)

where we assume $\tan {(\eta \,t_{0})}=-\eta$ and $\tan {(\eta \,t_{n})}=\eta$. Therefore, in these coordinates the metric is tri-diagonal. Let us first of all analyze the off-diagonal terms. An elementary calculation shows that these terms have the form $-\eta \frac{e^{-i\eta \, (t_j-t_{j-1})}}{\sin {(\eta \,(t_j-t_{j-1}))}} \,dZ_j \,d{\overline{Z}}_{j-1}$. Let us denote the part of the Kähler potential, which describes these terms, by $K(Z_j, {\overline{Z}}_j, Z_{j-1}, {\overline{Z}}_{j-1})$. It is not difficult to see that

$$\begin{aligned} K(Z_j, {\overline{Z}}_j, Z_{j-1}, {\overline{Z}}_{j-1})=i\,\eta (Z_j {\overline{Z}}_{j-1}-{\overline{Z}}_j Z_{j-1})+{1\over 2\eta }\,P(2\eta (t_j-t_{j-1})),\nonumber \\ \end{aligned}$$

(3.45)

then P satisfies $P''(t)={1\over 2}\,\mathrm {ctg}{({t\over 2})}$. Next, we come to the diagonal terms. A typical diagonal term has the form

$$\begin{aligned}&{\eta \over \cos {(\eta \,t_{j})}}\,\left( \frac{\cos {(\eta \,t_{j-1})}}{\sin {(\eta (t_j-t_{j-1}))}}+\frac{\cos {(\eta \,t_{j+1})}}{\sin {(\eta (t_{j+1}-t_{j}))}}\right) \,dZ_j \,d{\overline{Z}}_{j}\\&\quad =\eta \,\left( \mathrm {ctg}{(\eta \,(t_j-t_{j-1}))} +\mathrm {ctg}{(\eta \,(t_{j+1}-t_{j}))}\right) \,dZ_j. \,d{\overline{Z}}_{j}. \end{aligned}$$

These terms come from the differentiation of the ‘pairwise’ potentials ${\widetilde{K}}(Z_j, {\overline{Z}}_j, Z_{j-1}, {\overline{Z}}_{j-1})+{\widetilde{K}}(Z_{j+1}, {\overline{Z}}_{j+1}, Z_{j}, {\overline{Z}}_{j})$, so there is no extra contribution. As a result, we get expression (3.38) for the full Kähler potential. $\square$

Finally, we are in a position to resolve the ‘paradox’ observed in Sect. 3.2. The question was: How is it possible to get a non-Kähler toric manifold after performing T-duality on all angles of a toric Kähler manifold? Indeed, this would not have been possible if the Kähler potential was invariant under the action of the torus (in which case it would have form (3.15)). In the case at hand, however, potential (3.38) is not invariant under the action of the torus. This is due to the non-invariance of the first term, quadratic in the $Z_j, \overline{Z_j}$, as the imaginary parts of $Z_j$ are the angles. Under a shift of an angular variable, the Kähler potential shifts by terms linear in $Z_j, \overline{Z_j}$, which do not contribute to the metric. As a result, the metric is still invariant. A related fact is that the moment map variables are not well-defined, as the $(\mathbb {CP}^{n-1})^\vee$ is not simply connected. Indeed, a standard argument says that, if a vector field $\xi$ preserves the symplectic form $\Omega$, i.e., ${\mathcal {L}}_\xi \Omega =0$, it follows that $d(i_\xi \Omega )=0$. If the manifold is simply-connected, or more generally if $[i_\xi \Omega ]=0\in H^1({\mathcal {M}}, {\mathbb {R}})$, one can define a moment map $\mu$ by $i_\xi \Omega =d\mu$. In the present case $[i_\xi \Omega ]\ne 0\in H^1({\mathcal {M}}, {\mathbb {R}})$, as can be easily seen from expression (3.41) for the symplectic form. Indeed, $i_{\partial \over \partial \psi _j}\Omega =\frac{ dx_j}{2 x_j}-\eta \,\sum \nolimits _{k}\, (i\,{\mathcal {R}}_{jk})\, d\psi _k$, so that the would-be moment map variables $\mu _j$ turn out to be linear in the angles for $\eta \ne 0$ and $n>2$. In this situation, the Kähler metric inevitably has cross-terms between the angular variables $\psi$ and the radial variables x, which produce a non-topological B-field upon T-duality.

3.4 Ricci flow

We are now in a position to prove that the $\eta$-deformed metric satisfies the Ricci flow equation, if the parameter $\eta$ is assumed to flow accordingly. To simplify the notation, in potential (3.38) we make a rescaling $t_j\rightarrow {t_j\over 2 \eta }$ and drop the overall factor of $1\over 4\eta$. The dependence on $\eta$ is now only hidden in the dependence of the non-dynamical parameters $t_0, t_n$: $\tan {({t_0\over 2})}=-\eta ,\;\tan {({t_n\over 2})}=\eta$. More importantly, we make a shift $t_k\rightarrow t_k+2k\tau$, to arrive at the following statement:

Proposition 4

The metric described by the Kähler potential

$$\begin{aligned} {\mathcal {K}}=\sum \limits _{j=2}^{n-1}\,i\,(Z_j {\overline{Z}}_{j-1} -{\overline{Z}}_j Z_{j-1})+2\,\sum \limits _{j=1}^n\,P\left( t_j-t_{j-1}+2\tau \right) , \end{aligned}$$

(3.46)

where $P(t)=i\left( {\mathrm {Li}}_2(e^{i t})+{t(2\pi -t)\over 4}\right)$, satisfies the Ricci flow equation ${d g_{i{\overline{j}}}\over d\tau }=4\,R_{i{\overline{j}}}$.

Proof

For brevity, it will be convenient to denote $a_j:=\mathrm {ctg}({t_j-t_{j-1}\over 2}+\tau )$. After the shift, the components of the Hermitian metric are

The determinant $d_k$ of a tri-diagonal matrix of size $k\times k$ satisfies a well-known recursion relation $d_{k+1}=A_{k+1}\,d_k-B_kC_k\,d_{k-1}$ (where $A_k$ are the diagonal values and $B_k, C_k$ are the values on the leading sub/superdiagonals). In our case, one computes directly $d_1=\frac{\sin {({t_2-t_0\over 2}+2\tau )}}{\sin {({t_1-t_0\over 2}+\tau )}\sin {({t_2-t_1\over 2}+\tau )}}$ and $d_2=\frac{\sin {({t_3-t_0\over 2}+3\tau )}}{\sin {({t_1-t_0\over 2}+\tau )}\sin {({t_2-t_1\over 2}+\tau )}\sin {({t_3-t_2\over 2}+\tau )}}$. Using elementary trigonometric identities, one can then check that the expression

$$\begin{aligned} d_k=\frac{\sin {\left( {t_{k+1}-t_0\over 2}+(k+1)\,\tau \right) }}{\prod \nolimits _{j=1}^{k+1}\,\sin {\left( {t_j-t_{j-1}\over 2}+\tau \right) }} \end{aligned}$$

(3.47)

satisfies the recursion relation. Therefore, the determinant is ${\mathrm {det}}\,g=d_{n-1}$. Note that $t_0$ and $t_n$ are constant parameters, which leads to the following expression for the Ricci tensor:

$$\begin{aligned} R_{i{\overline{j}}}=-\,\partial _i\partial _{{\overline{j}}}\log {({\mathrm {det}}\,g)} =\partial _i\partial _{{\overline{j}}}\left( \sum \limits _{j=1}^n\,\log {\left( \sin {\left( {t_j-t_{j-1}\over 2}+\tau \right) }\right) }\right) . \end{aligned}$$

(3.48)

Since $P''(t)={1\over 2}\mathrm {ctg}({t\over 2})$, it follows that $P'(t)=\log {(\sin {t\over 2})}$, so that the Ricci potential is $1\over 4$ times the derivative of the Kähler potential w.r.t. $\tau$. The assertion follows immediately. $\square$

Comment Note that the Ricci flow equation is satisfied without the need for introducing any compensating vector field $\xi ^\mu$, or the dilaton $\Phi$.

3.4.1 The complex hyperbolic space

As a preparation for the discussion of what the Ricci flow really does to the metric, let us consider one more limit of the metric (3.46). We set $\tau =0$ and consider the following limit: $t_0, t_1, \ldots , t_S\rightarrow -\pi$, $t_{S+1}, \ldots , t_{n-1}, t_n\rightarrow \pi$. Note that since $\tan \frac{t_n}{2}=\eta$ and $\tan \frac{t_0}{2}=-\eta$, this limit implies $\eta \rightarrow \infty$. We denote $\pi -t_n:=\epsilon$ and rescale all variables accordingly: $t_j=-\pi +\epsilon \,\hat{t}_j$ for $j=0, \ldots , S$ and $t_j=\pi +\epsilon \,\hat{t}_j$ for $j=S+1, \ldots , n$. Taking into account that $t_0=-t_n$, we find $\hat{t}_0=1$ and $\hat{t}_n=-1$. The Kähler potential takes the form

$$\begin{aligned} \mathcal {K}= & {} \epsilon ^2\,\sum \limits _{j=1}^n\,{i\over 2}\,(\hat{Z}_j \overline{\hat{Z}}_{j-1}-\overline{\hat{Z}}_j \hat{Z}_{j-1})\\&+\epsilon \,\left( \sum \limits _{\begin{array}{c} j=1, \\ j\ne S+1 \end{array}}^n\,(\hat{t}_j-\hat{t}_{j-1})\log {(\hat{t}_j-\hat{t}_{j-1})} -(\hat{t}_S-\hat{t}_{S+1})\log {(\hat{t}_S-\hat{t}_{S+1})}\right) \end{aligned}$$

(since $\hat{t}_S\ge 0$ and $\hat{t}_{S+1}\le 0$, the difference $\hat{t}_S-\hat{t}_{S+1}\ge 0$). Denoting $\mu _j:={1\over 2}(\hat{t}_j-\hat{t}_{j-1})$ and dropping the first term as subleading, we get

$$\begin{aligned} \mathcal {K}\sim 2\epsilon \sum \limits _{\begin{array}{c} j=1 \end{array}}^n\,\mu _j\,\log {|\mu _j|},\quad \quad \sum \limits _{j=1}^n\,\mu _j=-1,\quad \quad \mu _{j\ne S+1}\ge 0, \quad \quad \mu _{S+1}\le 0 \,.\qquad \end{aligned}$$

(3.49)

This expression coincides with the symplectic potential of the complex hyperbolic space $U(1, n-1)\over U(1)\times U(n-1)$ (compare with an analogous expression (3.19) for the case of $\mathbb {CP}^{n-1}$) and can be easily verified using its Kähler potential $\mathcal {K}_0=\log {\left( 1-\sum \limits _{j=1}^{n-1}\,|W_j|^2\right) }$. This means that the original manifold $\mathbb {CP}^{n-1}_\eta$ coincides, in this limit, with the complex hyperbolic space. In the case of $\mathbb {CP}^1_\eta$ this was observed in [22]. The factor of $\epsilon$ in front in the formula (3.49) indicates that the manifold shrinks in the limit $\epsilon \rightarrow 0$ (i.e. $\eta \rightarrow \infty$), just like it does in the limit $\eta \rightarrow 0$.

Note that there are n ways to take the limit that we just described. They correspond to the number of ways to split the times $t_1, \ldots , t_{n-1}$ into two groups, as above, i.e. $S=0, \ldots , n-1$. This is easy to understand at the example of the sphere $\mathbb {CP}^1$, i.e. when $n=2$. In this case one should consider the metric (3.21) in the limit $s\rightarrow -1$. Then one arrives at two copies of the Poincaré disc, which correspond to the cases $|W|<1$ and $|W|>1$. These are of course connected by the equator $|W|=1$, which serves as the common boundary of the two discs – it is at infinite distance.

3.4.2 Endpoints of the Ricci flow

Earlier we considered the Ricci flow for the Kähler metric on $(\mathbb {CP}^{n-1}_\eta )^\vee$. From proposition 4, after shifting the t-variables $t_k\rightarrow t_k-(2k-n)\tau$, we see that the only effect of the flow is that $t_n=n\tau$ (and $t_0=-n\tau$). Therefore $\eta =\tan {({t_n\over 2})}=\tan {({n\tau \over 2})}$, and the solution interpolates between two endpoints: $t_n=0$ ($\eta \rightarrow 0$) and $t_n=\pi$ ($\eta \rightarrow \infty$). As the solution approaches $t_n=0$, i.e. when $t_n=\epsilon$ is small and positive, since all the variables satisfy $-\epsilon \le t_k\le \epsilon$, one should rescale these variables $t_k\rightarrow \epsilon \, t_k$ and take the limit $\epsilon \rightarrow 0$. This is the same as taking the $\eta \rightarrow 0$ limit in the original potential (3.38). As was described in the Comment after Proposition 3, the resulting geometry is that of the undeformed $(\mathbb {CP}^{n-1})^\vee$. The other limit, $t_n\rightarrow \pi$, corresponds to $\eta \rightarrow \infty$.

The general properties of T-duality guarantee that the original $\eta$-deformed geometry also satisfies the Ricci flow equations [54, 55]. In order to analyze the implications of the Ricci flow for the original geometry, one should recall that, in the process of performing T-duality, a dilaton $\Phi (\mu )=-{1\over 2}\log {\mathrm {det}({\partial ^2 \mathcal {K}\over \partial t^2})}\big |_{t\rightarrow \mu }$ is generated [75] (according to our conventions, we relabel the $t_j$-variables as $\mu _j$ upon passing to the original manifold $\mathbb {CP}^{n-1}_\eta$). It contributes to the Ricci flow equation in the original frame, but its effect is fully accounted by the evolution of coordinates according to the gradient flow equation ${d \mu ^k\over d\tau }=-g^{km}\partial _m\Phi$ (cf. [83]). Although we do not demonstrate it here in full generality, we believe that the solutions $\mu _k(\tau )$ behave, in the limit $t_n=n\tau \rightarrow \pi$, as described in the previous section, namely the set $(\mu _1, \ldots , \mu _{n-1})$ splits into two groups, the variables from each group approaching the values $-\pi$ and $\pi$, respectively.

As a justification of this claim, we consider the case $n=2$, where this effect can already be observed. The metric of $(\mathbb {CP}^1_\eta )^\vee$ is (we encountered it in Sec. 3.2.2)

$$\begin{aligned} (ds^2)^{\vee }=\sin {(2\tau )}\,\frac{{1\over 4}\,dt^2+d\phi ^2}{\cos (t)-\cos {(2\tau )}}\,. \end{aligned}$$

(3.50)

If we perform T-duality on $\phi$, we get the dilaton $\Phi =-{1\over 2}\log {\left( \frac{\sin {(2\tau )}}{\cos (\mu )-\cos {(2\tau )}}\right) }$ (where we have relabelled t by $\mu$, since it has the meaning of moment map on $\mathbb {CP}^1_\eta$). The dilaton-induced gradient flow then takes the form

$$\begin{aligned} {d \mu \over d\tau }=-g^{00}\frac{\partial \Phi }{\partial \mu }={2\sin {\mu }\over \sin {(2\tau )}}\,, \end{aligned}$$

(3.51)

and as a result $e^{\widetilde{t}}:=\frac{\sin (\tau +{\mu \over 2})}{\sin (\tau -{\mu \over 2})}$ is a constant along the flow. The metric on $\mathbb {CP}^1_\eta$, obtained by T-dualizing (3.50), has the form $ds^2={1\over 4}\left( \,\frac{\sin {(2\tau )}}{\cos (\mu )-\cos {(2\tau )}}\right) \,d\mu ^2+\left( \,\frac{\sin {(2\tau )}}{\cos (\mu )-\cos {(2\tau )}}\right) ^{-1}d\phi ^2=\sin {(2\tau )}\,\frac{{1\over 4}d\widetilde{t}^{\,\,2}+d\phi ^2}{\cosh {\widetilde{t}}+\cos {(2\tau )}}$. This metric, when expressed in the $\widetilde{t}$-variable, satisfies the pure Ricci flow equation (just like $(ds^2)^\vee$ in (3.50)) and interpolates between the sphere metric at $\tau =0$ and the Lobachevsky metric at $\tau ={\pi \over 2}$. The two attractor sets referred to above correspond to $\mu >0$ and $\mu <0$ or, equivalently, to $\widetilde{t}\in (-\infty , 0)$ and $\widetilde{t} \in (0, \infty )$. At $\tau ={\pi \over 2}$ these are two copies of the Lobachevsky plane, the border between them being at $\mu =0$.

For higher n the $\eta$-deformed model will interpolate, along the Ricci flow, between $\mathbb {CP}^{n-1}$ with its Fubini-Study metric and the complex hyperbolic space $U(1, n-1)\over U(1)\times U(n-1)$ with the Bergman metric, described in the previous section.

Another possibility is to consider a sausage-like deformation, which means taking $\eta$ imaginary, as explained earlier in Sec. 3.2.2. From the point of view of the Kähler potential, it suffices to make a replacement $\eta \rightarrow -i\,\eta$. Note however that, after such a replacement, the function $\mathcal {K}$ is no longer real, which reflects the fact that the deformation is not unitary, and the ‘metric’ has an imaginary part (so it should more properly be referred to as a non-degenerate bilinear form on the tangent space). This is the regime studied in [44, 45], and within this approach one can analyze the $\sigma$-model as a deformation of a conformal field theory. Just like we did earlier in the unitary case, we rescale the variables $t_k\rightarrow {t_k \over 2\eta }$ and, accordingly, $Z_k \rightarrow {Z_k \over 2\eta }$, so as to get rid of the parameter $\eta$ in most places. We then get the Kähler potential in this regime:

$$\begin{aligned}&\mathcal {K}=\sum \limits _{j=1}^n\,(Z_j \overline{Z}_{j-1}-\overline{Z}_j Z_{j-1})+2\,\sum \limits _{j=1}^n\,\widetilde{P}(t_j-t_{j-1})\,,\quad \quad t_j\ge t_{j-1}\,,\\&\quad \text {where}\quad \quad \widetilde{P}(t)=\mathrm {Li}_2(e^{-t})+{t^2\over 4}\,, \quad \quad \text {and} \quad \quad t_j:=Z_j+\overline{Z}_j \,.\nonumber \end{aligned}$$

(3.52)

One still has the restrictions $t_0 \le t_1\le \cdots \le t_{n-1}\le t_n$, albeit without an upper bound on $t_n$. The Ricci flow looks exactly as before, i.e. provided one replaces $t_k\rightarrow 2k\tau +t_k$, the Kähler potential satisfies the Ricci flow equation in $\tau$. Let us now analyze the endpoints of the Ricci flow, starting with the limit $\tau \rightarrow \infty$. In the shifted variables the dilogarithms entering the Kähler potential are of the form $\mathrm {Li}_2(e^{-(t_j-t_{j-1}+2\tau )})$, and they all vanish in the limit $\tau \rightarrow \infty$, since $\mathrm {Li}_2(x)\sim x$ for $x\rightarrow 0$. Besides, the range restriction on the shifted variables is $t_j\ge t_{j-1}-2\tau$, so the constraints are lifted in the limit $\tau \rightarrow \infty$. Asymptotically, the potential looks as follows (dropping all irrelevant terms):

$$\begin{aligned} \mathcal {K}\sim \sum \limits _{j=1}^n\,(Z_j \overline{Z}_{j-1}-\overline{Z}_j Z_{j-1})+\sum \limits _{j=1}^n\,{(t_j-t_{j-1})^2\over 2}\sim 2\,\sum \limits _{j=1}^n\,(|Z_j|^2-\overline{Z}_j Z_{j-1})\,.\nonumber \\ \end{aligned}$$

(3.53)

In this formula $Z_0=Z_n=0$. This is a potential for a flat ‘metric’ on an $(n-1)$-dimensional cylinder $(\mathbb {C}^\times )^{n-1}$, meaning that the $\sigma$-model is free in this regime, although non-unitary. The limit $\tau \rightarrow 0$ of the Ricci flow may be taken exactly as for the unitary case and produces the undeformed space $(\mathbb {CP}^{n-1})^{\vee }$.

3.5 The $\mathbb {CP}^{n-1}$-model as a $\beta \gamma$-system and its deformation

Apart from the deformation described in the previous sections, there is another integrable deformation of the $\mathbb {CP}^{n-1}$-model that can be described by considering the latter as a coupling of two $\beta \gamma$-systems [4]. (see also [84, 85]) for related developments). It is convenient to start with the gauged linear sigma-model (GLSM) formulation of the model, which was constructed in [86]. In the case of the $\mathbb {CP}^{n-1}$-model, one starts with three matrices $U\in \mathrm {Hom}(\mathbb {C}, \mathbb {C}^n),\, V\in \mathrm {Hom}(\mathbb {C}^n, \mathbb {C}),\, \Phi \in \mathrm {End}(\mathbb {C}^n)$. In other words, U is a column vector and V is a row vector, whereas $\Phi$ is an $n\times n$-matrix. Inspired by [4], we start from the $\beta \gamma$-system Lagrangian of the following form:

$$\begin{aligned} {\mathscr {L}}=\mathrm {Tr}\left( V \overline{{\mathscr {D}}} U\right) +\mathrm {Tr}\left( V \overline{{\mathscr {D}}} U\right) ^\dagger +\mathrm {Tr}\left( r_s^{-1}(\Phi _z) \Phi _{{\overline{z}}}\right) , \end{aligned}$$

(3.54)

where $\overline{{\mathscr {D}}}$ is the “elongated” covariant derivative $\overline{{\mathscr {D}}} U={\overline{\partial }}U+i \,U {\mathcal {A}}_{{\overline{z}}}+i\,\Phi _{{\overline{z}}} U$ and $r_s$ is the classical r-matrix, depending on the deformation parameter s, that we already encountered in the previous sections. One can eliminate the auxiliary field $\Phi$ that enters the Lagrangian quadratically. As a result, one arrives at the following:

$$\begin{aligned} {\mathscr {L}}= & {} \mathrm {Tr}\left( V {\overline{D}} U\right) +\mathrm {Tr} \left( V {\overline{D}} U\right) ^\dagger -\mathrm {Tr}\left( r_s(U\otimes V) (U\otimes V)^\dagger \right) , \end{aligned}$$

(3.55)

$$\begin{aligned}&{\text {where}}\quad \quad {\overline{D}} U={\overline{\partial }}U+i\, U{\mathcal {A}}_{{\overline{z}}}. \end{aligned}$$

(3.56)

Note that the latter is the usual GLSM $\mathbb {C}^\times$-covariant derivative. We are talking about $\mathbb {C}^\times$ rather than U(1) as the gauge group, since so far no normalization condition on U is assumed.

Following [4], we can construct a family of flat connections by the following procedure. Define

$$\begin{aligned} {\mathscr {A}}=r_{\kappa _1}(J_z)\,dz-r_{\kappa _2}(J_{{\overline{z}}})\,d{\overline{z}}. \end{aligned}$$

(3.57)

Here, $\kappa _1, \kappa _2$ are complex parameters that will be related below, and J is a certain one-form, which in the undeformed case, when $r_s\sim \mathbbm {1}$, coincides with the Noether current one form of model (3.55): $J=J_z\,dz+J_{{\overline{z}}}\,d{\overline{z}}=UV\,dz-V^\dagger U^\dagger \,d{\overline{z}}.$ The connection ${\mathscr {A}}$ is flat, if two requirements are fulfilled. First, the currents satisfy the equations

$$\begin{aligned}&{\overline{\partial }}J_z=[r_{s^{-1}}(J_{{\overline{z}}}), J_z],\quad \quad \partial J_{{\overline{z}}}=[J_{{\overline{z}}}, r_s(J_z)]. \end{aligned}$$

(3.58)

These equations follow from the equations of motion of model (3.55). Besides, the matrix r has to obey the equation

$$\begin{aligned} r_{\kappa _2}([J_{{\overline{z}}}, r_s(J_z)])+r_{\kappa _1}([r_{s^{-1}}(J_{{\overline{z}}}), J_z])+[r_{\kappa _1}(J_z), r_{\kappa _2}(J_{{\overline{z}}})]=0. \end{aligned}$$

(3.59)

This can be identified with the classical Yang–Baxter equation (CYBE) written out in “Appendix A,” if one identifies the parameters as $\kappa _1=e^u,\; \kappa _2=e^{u+v},\; e^v=s^{-1}$. In particular, this implies $\kappa _1=\kappa _2\,s.$ In the trigonometric case, the r-matrix satisfying this equation is given by (3.12).

Deformation (3.55) is generally different from the $\eta$-deformation that we considered earlier. The case where the two deformations coincide is $n=2$, i.e., when we are again in the situation of the deformed sphere $\mathbb {CP}^1$. The reason why the Lagrangian (3.11) in this case leads to the same theory is that its last line vanishes for $n=2$. Indeed, consider the term $\mathrm {Tr}(U\otimes {\overline{V}}\,\rho (U\otimes {\overline{W}}))=\sum \nolimits _{i, j}\,U_i {\overline{V}}_j U_j {\overline{W}}_i (1-\eta \,{\mathcal {R}}_{ji})=-{\eta \over 2}\,\sum \nolimits _{i, j}\,U_i U_j \,{\mathcal {R}}_{ji}\,({\overline{V}}_j {\overline{W}}_i-{\overline{V}}_i {\overline{W}}_j )$, where we took into account that the vectors U and V are orthogonal, ${\overline{V}}\circ U=0$. The case $n=2$ is special for the following reason: Since both V and W are orthogonal to U, they have to be collinear, thereby leading to the vanishing of the combination in brackets in the above formula. Integrating out V and W from the remaining terms will produce, after some simple rewritings, a model equivalent to the one of (3.55). In fact, the authors of [4] used, in their Section 6.3, exactly the formalism of (3.55) to derive the sausage model.

On the other hand, model (3.55) for $n>2$ is subject to the so-called Pontryagin anomaly [87, 88], as was also mentioned in [4]. The anomaly is governed by the fact that $p_1(\mathbb {CP}^{n-1})\ne 0$ for $n>2$. For a discussion of fermionic generalizations of the models (in which this issue is likely resolved), as well as $\beta$-functions, Ricci flow, etc. see [89].

4 Flag manifold models and Toda field theories

In the previous sections, we discussed in detail the $\eta$-deformation of $\mathbb {CP}^{n-1}$ target spaces. It would be desirable to eventually extend those results to the case of generic flag manifold target spaces. As a first step in this direction, we turn to the analysis of the Pohlmeyer map for complete flag manifolds

$$\begin{aligned} {\mathcal {M}}=\frac{U(n)}{U(1)^n}, \end{aligned}$$

(4.1)

which, in a sense, is the case polar to the one of symmetric target spaces (for $n>2$). A point in this manifold is an n-tuple of ordered orthonormal vectors in $\mathbb {C}^n$: $(u_1, \ldots , u_n):=g$, which we have grouped into a unitary matrix g. It is customary to introduce a Maurer–Cartan current $J=g^{-1}dg$ that satisfies the zero-curvature equation $dJ+J\wedge J=0$. Let us also introduce the notation $G=U(n), \;H=U(1)^n$, the corresponding Lie algebras being ${\mathfrak {g}}$ and ${\mathfrak {h}}$. Now,

$$\begin{aligned} {\mathfrak {g}}= & {} {\mathfrak {h}}\oplus {\mathfrak {m}}\quad \quad \quad \;\;\; ({\mathfrak {m}}= \text {off-diagonal matrices})\end{aligned}$$

(4.2)

$$\begin{aligned} {\mathfrak {m}}= & {} {\mathfrak {m}}_+\oplus {\mathfrak {m}}_- \quad \quad ({\mathfrak {m}}_\pm = \text {upper/lower-triangular matrices}). \end{aligned}$$

(4.3)

We can decompose the current accordingly: $J=J_0+J_++J_-$. We will take the $\sigma$-models of [1,2,3] as the relevant generalizations of symmetric space $\sigma$-models. As shown in [3], the e.o.m. of these models may be concisely written as (here ${\mathscr {D}}$ is the H-covariant derivative)

$$\begin{aligned}&\overline{{\mathscr {D}}}(J_+)_z-[(J_+)_z, (J_+)_{{\overline{z}}}]=0.\end{aligned}$$

(4.4)

$$\begin{aligned}&{\mathscr {D}}(J_-)_{{\overline{z}}}+[(J_-)_z, (J_-)_{{\overline{z}}}]=0. \end{aligned}$$

(4.5)

The projection of the zero-curvature condition $dJ+J\wedge J=0$ onto ${\mathfrak {m}}_-$ has the form

$$\begin{aligned} {\mathscr {D}}(J_-)_{{\overline{z}}}-\overline{{\mathscr {D}}}(J_-)_z+[(J_-)_z, (J_-)_{{\overline{z}}}]+[(J_+)_z, (J_-)_{{\overline{z}}}]_{{\mathfrak {m}}_-}+[(J_-)_z, (J_+)_{{\overline{z}}}]_{{\mathfrak {m}}_-}=0.\nonumber \\ \end{aligned}$$

(4.6)

Taking into account (4.4), we obtain

$$\begin{aligned} \overline{{\mathscr {D}}}(J_-)_z-[(J_+)_z, (J_-)_{{\overline{z}}}]_{{\mathfrak {m}}_-}-[(J_-)_z, (J_+)_{{\overline{z}}}]_{{\mathfrak {m}}_-}=0. \end{aligned}$$

(4.7)

We can now derive an important conservation law. First of all, (4.4) implies that $\overline{{\mathscr {D}}}(J_+)_z\in [{\mathfrak {m}}_+, {\mathfrak {m}}_+]$; therefore, $\overline{{\mathscr {D}}}(J_z)_{i,i+1}=0, \;\;i=1, \ldots n-1$. Besides, (4.7) implies that $\overline{{\mathscr {D}}}(J_-)_z\in {\mathfrak {m}}_-\cap [{\mathfrak {m}}_+, {\mathfrak {m}}_-]$, so that $\overline{{\mathscr {D}}}(J_z)_{n, 1}=0$. This leads to the conservation law ${\overline{\partial }}\left( \prod \nolimits _{i=1}^n\,(J_z)_{i, i+1} \right) =0,$ where we have assumed a cyclic labeling of the currents, $J_{n, n+1}\equiv J_{n, 1}$. Using conformal invariance and assuming that $(J_{i, i+1})_z\ne 0$ for all i, we may set

$$\begin{aligned} \prod \limits _{i=1}^n\,(J_z)_{i, i+1}=1. \end{aligned}$$

(4.8)

This is a generalization to arbitrary n of Pohlmeyer’s constraint (2.2). The constraint can be ‘solved’ by setting

$$\begin{aligned} (J_{i, i+1})_z=e^{X_{i}-X_{i+1}},\quad \quad X_i\in \mathbb {C}\quad \text {mod}\quad 2\pi i\,{\mathbb {Z}}. \end{aligned}$$

(4.9)

Note that the definition of the flag manifold implies a gauge symmetry $u_k\rightarrow e^{i\alpha _k} \,u_k$. In terms of the variables $X_i$, this is a shift symmetry $X_k\rightarrow X_k-i\,\alpha _k$. In particular, a suitable gauge is taken by assuming that these variables are real: $X_k\in {\mathbb {R}}.$ In what follows, this choice of gauge will be implied.

The equations $\overline{{\mathscr {D}}}(J_z)_{i,i+1}=0$ may now be solved by identifying ${\overline{u}}_i \circ {\overline{\partial }}u_i=-{\overline{\partial }}X_i$. In other words, in the new variables the connection $A_k=i \,J_{kk}=i {\overline{u}}_k \circ d u_k$ entering the covariant derivative ${\mathscr {D}}$ may be written as

$$\begin{aligned} A_k=i \,J_{kk}=i (\partial X_k \,dz-{\overline{\partial }}X_k \,d{\overline{z}}). \end{aligned}$$

(4.10)

4.1 Toda parametrization

In this section, we consider the simplest (non-symmetric) flag manifold $U(3)\over U(1)^3$. We will assume that ${\prod \limits _{i=1}^3\,(J_z)_{i, i+1} \ne 0}$, so that (4.8) may be achieved by a conformal transformation.⁷

The expression for $J_z$ in the X-variables has the form:

$$\begin{aligned} J_z= \begin{pmatrix} \partial X_1 &{}\quad e^{X_1-X_2}&{}\quad (J_{13})_z\\ (J_{21})_z &{}\quad \partial X_2 &{}\quad e^{X_2-X_3}\\ e^{X_3-X_1}&{}\quad (J_{32})_z &{}\quad \partial X_3 \end{pmatrix},\quad \quad \quad J_{{\overline{z}}}=-J_z^\dagger . \end{aligned}$$

(4.11)

$(J_+)_z$ and $(J_-)_z$ are, respectively, the upper- and lower-triangular parts of the above matrix, and $(J_+)_{{\overline{z}}}=-((J_-)_z)^\dagger$, $(J_-)_{{\overline{z}}}=-((J_+)_z)^\dagger$. To write down the equations, we introduce the ‘twisted currents’ $(U_{21})_z=e^{X_1-X_2} (J_{21})_z, (U_{13})_z=e^{X_3-X_1} (J_{13})_z, (U_{32})_z=e^{X_2-X_3} (J_{32})_z$. The first equation (4.4) then gives:

$$\begin{aligned} {\overline{\partial }}(U_{13})_z+e^{2(X_3-X_2)}\,\bar{(U_{32})_z} -e^{2(X_2-X_1)}\,\bar{(U_{21})_z}=0. \end{aligned}$$

(4.12)

The remaining equations, which follow from (4.7), are

$$\begin{aligned}&{\overline{\partial }}(U_{21})_z+e^{2(X_1-X_3)}\,\bar{(U_{13})_z}-e^{2(X_3-X_2)} \,\bar{(U_{32})_z}=0,\end{aligned}$$

(4.13)

$$\begin{aligned}&{\overline{\partial }}(U_{32})_z-e^{2(X_1-X_3)}\,\bar{(U_{13})_z}+e^{2(X_2-X_1)} \,\bar{(U_{21})_z}=0 \end{aligned}$$

(4.14)

The equations imply the conservation law ${\overline{\partial }}((U_{13})_z+(U_{21})_z+(U_{32})_z)=0$, where $T_{zz}:=(U_{13})_z+(U_{21})_z+(U_{32})_z$ is the holomorphic component of the energy-momentum tensor.

One still has the equations arising from the ${\mathfrak {h}}$-projection of the zero-curvature equation ${dJ+J\wedge J=0}$:

$$\begin{aligned}&2 \,\partial {\overline{\partial }}X_1+e^{2(X_1-X_2)}-e^{2(X_3-X_1)}+e^{2(X_1-X_3)} \Vert (U_{13})_z\Vert ^2-e^{2(X_2-X_1)}\Vert (U_{21})_z\Vert ^2=0\nonumber \\&2 \,\partial {\overline{\partial }}X_2+e^{2(X_2-X_3)} -e^{2(X_1-X_2)}+e^{2(X_2-X_1)}\Vert (U_{21})_z\Vert ^2-e^{2(X_3-X_2)}\Vert (U_{32})_z\Vert ^2=0\nonumber \\&2 \,\partial {\overline{\partial }}X_3+e^{2(X_3-X_1)} -e^{2(X_2-X_3)}+e^{2(X_3-X_2)}\Vert (U_{32})_z\Vert ^2-e^{2(X_1-X_3)}\Vert (U_{13})_z\Vert ^2=0.\nonumber \\ \end{aligned}$$

(4.15)

These are the generalized Toda equations—a system describing the interaction of the Toda fields with the additional U-fields. In particular, if one sets $(U_{13})_z=(U_{21})_z=(U_{32})_z=0$, one obtains the pure Toda equations. Note that since the equations for $U_{ij}$ are of first order, a curious prospect would be in devising a fermionic interpretation for these variables.

In this section, we consider in detail the case $n=3$, but the results are generalizable to arbitrary n, that is, to flag manifolds of the type (4.1). It would also be interesting to construct an analogous parametrization for flag manifolds of arbitrary type, i.e., allowing for non-abelian denominators.

4.2 Toda reduction in the general case

In this section, we will derive a Toda field theory from a flag manifold $\sigma$-model for general n. In doing so, we will restrict ourselves to the pure Toda field theory, i.e., when all the additional U-fields are set to zero. For general n, this condition may be formulated, using the ${\mathbb {Z}}_n$-grading on the Lie algebra ${\mathfrak {g}}\simeq \mathfrak {su}_n$. The latter means a decomposition ${\mathfrak {g}}=\oplus _{i=0}^{n-1}\,{\mathfrak {g}}_i$, such that $[{\mathfrak {g}}_i, {\mathfrak {g}}_j]\subset {\mathfrak {g}}_{i+j\;\;\mathrm {mod}\;\; n}$. The subspaces ${\mathfrak {g}}_i$ are in fact uniquely determined by ${\mathfrak {g}}_1$, and we define ${\mathfrak {g}}_1=\mathrm {Span}(E_{i, i+1})_{i=1, \ldots n}$, where $E_{i, i+1}$ are the elementary ‘unit’-matrices, and $E_{n, n+1}\equiv E_{n, 1}$. It follows that ${\mathfrak {g}}_{-1}=\mathrm {Span}(E_{i+1, i})_{i=1, \ldots n}$ (again $E_{n+1, n}\equiv E_{1, n}$). The reduction to zero U-fields is then formulated as follows:

$$\begin{aligned} J_z\in {\mathfrak {g}}_0\oplus {\mathfrak {g}}_1,\quad \quad J_{{\overline{z}}}\in {\mathfrak {g}}_0\oplus {\mathfrak {g}}_{-1}\;. \end{aligned}$$

(4.16)

Therefore, $[(J_+)_z, (J_-)_{{\overline{z}}}]\in {\mathfrak {h}},\, [(J_-)_z, (J_+)_{{\overline{z}}}]\in {\mathfrak {h}}$, and equations (4.4), (4.7) reduce to ${\mathscr {D}}_{{\overline{z}}}(J_{i, i+1})_z=0$, which are automatically solved by (4.9), (4.10). The remaining non-trivial equations are the diagonal components of $dJ+J\wedge J=0$, and these are the Toda chain equations

$$\begin{aligned} 2\,\partial {\overline{\partial }}X_k-[J_z, J_{{\overline{z}}}]_{kk}=2\,\partial {\overline{\partial }}X_k+e^{2(X_k-X_{k+1})}-e^{2(X_{k-1}-X_k)}=0.\qquad \end{aligned}$$

(4.17)

In the literature on harmonic maps, cf. [61, 62], it has been observed that these Toda equations arise in the context of the so-called n-primitive maps to flag manifolds. These are maps $g: \Sigma \rightarrow {U(n)\over U(1)^n}$, whose associated current $J=g^{-1}dg$ satisfies the constraints (4.16). The virtue of our approach is that we have a full theory, of which the Toda chain is a subsector that can be described by simple constraints.

To illustrate the last point, let us derive the Lax pair of Flaschka–Manakov type from the Lax pair of the flag manifold $\sigma$-model. We start from the flag manifold generalization of Pohlmeyer’s family of flat connections (2.29) discussed earlier in the context of the $\mathbb {CP}^1$-model:

$$\begin{aligned} A_u= & {} {1-u\over 2} K_z dz+{1-u^{-1}\over 2} K_{{\overline{z}}} d{\overline{z}},\quad {\text {where}}\end{aligned}$$

(4.18)

$$\begin{aligned} K_z= & {} g\begin{pmatrix} 0 &{}\quad 2 \,(J_{12})_z &{}\quad 0 &{}\quad \cdots &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 2\,(J_{23})_z &{}\quad 0 &{}\quad \vdots \\ \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \vdots \\ 0 &{}\quad \cdots &{}\quad \cdots &{}\quad 0 &{}\quad 2 \,(J_{n-1, n})_z \\ 0 &{}\quad \cdots &{}\quad \cdots &{}\quad \cdots &{}\quad 0 \end{pmatrix}g^\dagger ,\quad \quad K_{{\overline{z}}}=-K_z^\dagger .\qquad \end{aligned}$$

(4.19)

Performing a gauge transformation by the group element g and introducing the X-variables according to (4.9), (4.10), we obtain

$$\begin{aligned}&{\mathscr {A}}_u\nonumber \\&\quad =\begin{pmatrix} {\overline{\partial }}X_1\,d{\overline{z}}-\partial X_1 \,dz &{}\quad -u \,e^{X_1-X_2}\,dz &{}\quad 0 &{}\quad \cdots &{}\quad e^{X_n-X_1}\,d{\overline{z}} \\ u^{-1} \,e^{X_1-X_2}\,d{\overline{z}} &{}\quad {\overline{\partial }}X_2\,d{\overline{z}}-\partial X_2 \,dz &{}\quad -u\,e^{X_2-X_3}\,dz &{}\quad 0 &{}\quad \vdots \\ 0 &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \vdots \\ \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \vdots \\ 0 &{}\quad \cdots &{}\quad \ddots &{}\quad {\overline{\partial }}X_{n-1}\,d{\overline{z}}-\partial X_{n-1} \,dz &{}\quad -u \,e^{X_{n-1}-X_n}\,dz \\ -e^{X_n-X_1}\,dz &{}\quad 0 &{}\quad \cdots &{}\quad u^{-1} \,e^{X_{n-1}-X_n}\,d{\overline{z}} &{}\quad {\overline{\partial }}X_n\,d{\overline{z}}-\partial X_n \,dz. \end{pmatrix}\nonumber \\ \end{aligned}$$

(4.20)

${\mathscr {A}}_u$ furnishes a one-parameter family of flat connections, describing Toda field theory. One can also perform a mechanical reduction by postulating ${\overline{\partial }}=\partial ={d\over dt}$, in which case one is led to the mechanical Toda chain [90]. If one additionally sets $u=1$, the zero-curvature equation (which in this case coincides with the flatness condition for J) takes the form discovered by Manakov [91] (in a different form by Flaschka [92])

$$\begin{aligned} {\dot{L}}=[L, M],\quad \quad {\text {where}}\quad \quad L=({\mathscr {A}}_{1})_{{\overline{z}}}-({\mathscr {A}}_{1})_{z},\quad M={1\over 2}\left( ({\mathscr {A}}_{1})_{{\overline{z}}}+({\mathscr {A}}_{1})_{z}\right) .\nonumber \\ \end{aligned}$$

(4.21)

For a review of mechanical Toda chains and their Lax representations, one can consult [93].

5 Conclusion and outlook

Let us summarize the main findings of the present paper, outlining some open problems and directions for future research. First, in Sect. 2 we consider a $\sigma$-model with a U(1)-invariant target space, construct its ‘Pohlmeyer-reduced’ cousin and show that the requirement of its integrability naturally leads, in a unique way, to the so-called sausage metric, first considered in [42]. It would be interesting to generalize this argument to higher-dimensional target spaces, for example to the case of the deformed $\mathbb {CP}^{n-1}$ model.

In Sect. 3, we study the $\eta$-deformed $\mathbb {CP}^{n-1}$ model, starting from ‘first principles.’ This manifold is toric, and it turned out useful to pass to the T-dual frame, i.e., to dualize all the angles simultaneously. Whereas the original geometry is generalized Kähler [46], we proved that the dual geometry is Kähler and derived its Kähler potential in explicit form. It would be interesting to derive the generalized Kähler potential for any n as well (the cases $n=2$ and $n=3$ were studied in [46]). At least when the Kähler potential is invariant under the action of the torus, the dual potential is given by a Legendre transform [79]. As explained at the end of Sect. 3.3, in our case the Kähler potential is not invariant, despite the fact that the metric is. On the other hand, the expression in [46] for the generalized Kähler potential at $n=3$ is strikingly similar to our expression (3.38), which is reminiscent of the phenomenon described in our lemma 2.

We then showed that the $\eta$-deformed metric satisfies the Kähler Ricci flow equation in the T-dual frame. The original geometry then interpolates, along the Ricci flow, between the $\mathbb {CP}^{n-1}$ manifold with its Fubini–Study metric and the complex hyperbolic space $U(1, n-1)\over U(1)\times U(n-1)$ with the Bergman metric. One can also achieve an ‘asymptotically free’ regime, if one chooses the deformation parameter to be imaginary.

Finally, in Sect. 4 we turn to the classically integrable $\sigma$-models with flag manifold target spaces, introduced by one of the authors [1,2,3]. We considered the class of complete flag manifolds and demonstrated that, if a certain non-degeneracy condition (4.8) holds, the model may be rewritten as a Toda field theory interacting with additional fields (which we call $U_{ij}$). The fact that the Toda chain arises in the context of harmonic maps into flag manifolds (the so-called primitive maps) has been known for a while [61, 62]; however, in Sect. 4 we derive this as a reduction ($U_{ij}=0$) of a complete nonlinear $\sigma$-model. The mapping of the flag manifold $\sigma$-model to the Toda chain is akin to Pohlmeyer’s reduction [43, 63,64,65], and it would be interesting to extend this map to the case of generic flag manifolds—a vast class ranging between complete flag manifolds and Grassmannians.

Appendix A: The classical Yang–Baxter equation

In its conventional form, the classical Yang–Baxter equation involves the classical r-matrix $r(u)\in {\mathfrak {g}}\otimes {\mathfrak {g}}$. The equation itself takes values in ${\mathfrak {g}}\otimes {\mathfrak {g}}\otimes {\mathfrak {g}}$ and has the following form:

$$\begin{aligned}{}[r_{12}(u), r_{13}(u+v)]+[r_{12}(u), r_{23}(v)]+[r_{13}(u+v), r_{23}(v)]=0. \end{aligned}$$

(A.1)

Here, we write the equation in additive form, i.e., when the spectral parameters u and v take values in $\mathbb {C}$. The notation $r_{12}(u)$ means $r_{12}(u)=r(u)\otimes \mathbbm {1}$, and analogously for other pairs of indices. Solutions to the above equation have been extensively investigated in the classical paper of Belavin and Drinfeld [94].

For the purposes of the present paper, it is more convenient to think of the r-matrix as a map $r: {\mathfrak {g}} \rightarrow {\mathfrak {g}}$, or equivalently $r\in \mathrm {End}({\mathfrak {g}})\simeq {\mathfrak {g}}\otimes {\mathfrak {g}}^*$. To rewrite the equation accordingly, first of all we expand the r-matrix in the basis of generators $\tau _a \in {\mathfrak {g}}$:

$$\begin{aligned} r(u)=\sum \limits _{i,\,j=1}^{{\mathrm {dim}}\,{\mathfrak {g}}} \,\lambda _{ij}(u)\,\tau _i\otimes \tau _j. \end{aligned}$$

(A.2)

The three terms in the equation can then be written as (we assume that the generators form an orthonormal basis w.r.t. the Killing metric, and $[\tau _a, \tau _b]=f_{abc}\,\tau _c$)

$$\begin{aligned} {[}r_{12}(u), r_{13}(u+v)]= & {} \sum \,\lambda _{ij}(u) \lambda _{mn}(u+v) [\tau _i, \tau _m]\otimes \tau _j\otimes \tau _n \end{aligned}$$

(A.3)

$$\begin{aligned} {[}r_{12}(u), r_{23}(v)]= & {} \sum \,\lambda _{ij}(u) \lambda _{mn}(v)\,f_{jms} \,\tau _i\otimes \tau _s \otimes \tau _n \end{aligned}$$

(A.4)

$$\begin{aligned} {[}r_{13}(u+v), r_{23}(v)]= & {} \sum \,\lambda _{ij}(u+v) \lambda _{mn}(v) \,f_{jns}\,\tau _i\otimes \tau _m\otimes \tau _s. \end{aligned}$$

(A.5)

We will now drop the index 12, 13, 23-notation and write $r_u(a)\in {\mathfrak {g}}$ for the r-matrix acting on a Lie algebra element $a\in {\mathfrak {g}}$. Inserting the Lie algebra elements a, b in the second and third slots of the equation, we obtain

$$\begin{aligned} {[}r_{12}(u), r_{13}(u+v)](a, b)= & {} [r_u(a), r_{u+v}(b)] \end{aligned}$$

(A.6)

$$\begin{aligned} {[}r_{12}(u), r_{23}(v)](a, b)= & {} r_u([r_v(b), a]) \end{aligned}$$

(A.7)

$$\begin{aligned} {[}r_{13}(u+v), r_{23}(v)](a, b)= & {} r_{u+v}([b, r_{-v}(a)]). \end{aligned}$$

(A.8)

To derive the last equality, we have used the assumed ‘unitarity’ property of the r-matrix: $\lambda _{ji}(u)=-\lambda _{ij}(-u)$. As a result, the CYBE takes the form

$$\begin{aligned} {[}r_u(a), r_{u+v}(b)]+r_u([r_v(b), a])+r_{u+v}([b, r_{-v}(a)])=0. \end{aligned}$$

(A.9)