Teaching Numerical Groundwater Flow Modeling with Spreadsheets

Abstract

The use of spreadsheets for numerical groundwater flow modeling is not a novelty; however, its potential in the classroom has not been emphasized enough. This Teachers Aid provides a step-by-step implementation of a steady-state, vertically integrated two-dimensional groundwater flow model in a confined irregular aquifer with boundary conditions of the three kinds and subject to pumping and recharge that will enhance the learning experience of students that are confronted for the first time with the numerical solution of the groundwater flow partial differential equation.

1 Introduction

The numerical solution of the groundwater flow equation using spreadsheets is not new. It was pioneered by Olsthoorn (1985), who, in his Ph.D. thesis (Olsthoorn 1999), recalls working on groundwater flow modeling using the Lotus 1,2,3 program as early as 1983. Since then, many papers have been written in which the use of spreadsheets for steady-state and transient groundwater modeling have been published; some examples are the works by Akhter et al. (2006), Ankor and Tyler (2019), Bair and Lahm (2006), Bhattacharjya (2011), Elfeki and Bahrawi (2015), Fox (1996), Karahan and Ayvaz (2005a), Karahan and Ayvaz (2005b), Molano (2014), Niazkar and Afzali (2015), Olsthoorn (1999), Ousey (1986).

In this paper, the emphasis is placed on the mechanics of building a model from scratch for someone who has no experience in numerical modeling or programming, starting by establishing the basic equation that governs groundwater flow in an aquifer and continuing with its implementation in an Excel spreadsheet.

The paper contains a description of the problem, the establishment of the numerical equations that provide the solution, a detailed implementation in Excel and a couple of examples. The paper ends discussing some potential extensions and conclusions.

2 The Problem

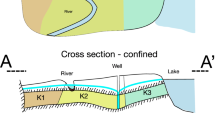
Consider the aquifer depicted in Fig. 1. It is a quasi-rectangular confined aquifer that is crossed by a river from north to south, impermeable in all its boundaries except for the east boundary, where it is in contact with a lake to which it is perfectly connected. There are three pumping wells, and there is also infiltration over the entire aquifer through a leaky confining layer. Aquifer transmissivity takes three different values in three zones as shown in the figure. It is assumed that the aquifer is at steady state.

Fig. 1

Aquifer sketch

The aquifer can be circumscribed by a rectangular mesh of 19 rows and 33 columns of 100 m by 100 m cells. The discretized representation of the aquifer is shown in Fig. 2.

Fig. 2

Aquifer discretization

The steady-state groundwater flow equation is nothing other than a balance equation that can be explicitly written in a generic cell considering the different flows that cross the cell borders. Figure 3 shows this generic cell that receives water from the adjacent cells at the north ($Q_N$), south ($Q_S$), east ($Q_E$) and west ($Q_W$) and also from the exterior ($Q_{Ext}$). Mass balance at steady state, assuming water of constant density, implies that

$$\begin{aligned} Q_N + Q_S + Q_E + Q_W + Q_{Ext} = 0. \end{aligned}$$

(1)

Fig. 3

A generic cell

The four flows entering through the sides are given by Darcy’s equation (Woessner and Poeter 2020, p. 25) and can be approximated by

$$\begin{aligned} Q_N\approx & {} T_N' \frac{h_N - h}{\varDelta }\varDelta , \end{aligned}$$

(2)

$$\begin{aligned} Q_S\approx & {} T_S' \frac{h_S - h}{\varDelta }\varDelta , \end{aligned}$$

(3)

$$\begin{aligned} Q_W\approx & {} T_W' \frac{h_W - h}{\varDelta }\varDelta , \end{aligned}$$

(4)

$$\begin{aligned} Q_E\approx & {} T_E' \frac{h_E - h}{\varDelta }\varDelta , \end{aligned}$$

(5)

where h is the hydraulic head at the generic cell, $h_N, h_S, h_W$ and $h_E$ are the hydraulic heads at the neighboring cells, $\varDelta$ is the cell width and height (in this case they are equal since the cells are squares), and $T_N', T_S', T_W'$ and $T_E'$ are the transmissivities at the cell interfaces. These transmissivities are generally approximated by the harmonic means of the transmissivities at both sides of the interface (Woessner and Poeter 2020, p. 166).

$$\begin{aligned} T_N'\approx & {} \frac{2T_N T}{T_N + T}, \end{aligned}$$

(6)

$$\begin{aligned} T_S'\approx & {} \frac{2T_S T}{T_S + T}, \end{aligned}$$

(7)

$$\begin{aligned} T_W'\approx & {} \frac{2T_W T}{T_W + T}, \end{aligned}$$

(8)

$$\begin{aligned} T_E'\approx & {} \frac{2T_E T}{T_E + T}, \end{aligned}$$

(9)

where T is the transmissivity of the generic cell and $T_N, T_S, T_W$ and $T_E$ are the transmissivities of the adjacent cells.

The external flow component $Q_{Ext}$ will have three components corresponding to the input water through the wells, through recharge and through the river.

$$\begin{aligned} Q_{Ext} = Q_{Well} + Q_{Inf} + Q_{Riv}, \end{aligned}$$

(10)

with

$$\begin{aligned} Q_{Well} = -W, \end{aligned}$$

(11)

where W [L$^{3}$T$^{-1}$] is the water flow being pumped at the cell,

$$\begin{aligned} Q_{Inf} = N \varDelta ^2, \end{aligned}$$

(12)

where N [LT$^{-1}$] is the net infiltration measured as water height per time, and

$$\begin{aligned} Q_{Riv} = \left\{ \begin{matrix} K'\frac{h_R - h }{b}A_{Riv},&{} h > h_B\\ K'\frac{h_R - h_B }{b} A_{Riv},&{} h \le h_B \end{matrix} \right. , \end{aligned}$$

(13)

where it is assumed that the river is connected to the aquifer through a semi-pervious riverbed of conductivity $K'$ and thickness b and whose bottom elevation is $h_b$; water infiltrates into the aquifer through the intersecting area of the riverbed with the cell $A_{Riv}$ (Harbaugh 2005, p. 6–6). The river stage is at $h_R$ and the piezometric head in the aquifer is at h; when h is above the riverbed bottom, then the flow into the aquifer is controlled by $h_R - h$, but if h is below the bottom, the river infiltration is independent of h and is computed as a function of $h_R - h_B$. The product $K' A_{Riv} b^{-1}$ [LT$^2$] is known as the riverbed conductance, R (Anderson et al. 1992, p. 126), and is the river parameter that has to be provided for each cell crossed by the river and that will control how much water goes from the river into the aquifer.

$$\begin{aligned} Q_{Riv} = \left\{ \begin{matrix} R(h_R - h ),&{} h > h_B\\ R(h_R - h_B),&{} h \le h_B \end{matrix} \right. . \end{aligned}$$

(14)

Substituting (234)–(13) into (1), the balance equation provides an expression for the hydraulic head at the generic cell as a function of the neighboring cell heads and the rest of the parameters mentioned.

$$\begin{aligned} h=\frac{T_N'h_N+T_S'h_S+T_W'h_W+T_E'h_E-W+N\varDelta ^2+Q_{Riv}}{T_N'+T_S'+T_W'+T_E'}. \end{aligned}$$

(15)

This is the equation that applies to all active cells in the aquifer and solves the groundwater flow equation under steady state and for a two-dimensional depth-integrated confined aquifer.

3 Implementation

The groundwater flow equation will be implemented in an Excel workbook containing the following 19 spreadsheets (the names used for the spreadsheets coincide with the ones used in the file provided and downloadable from the URL https://bit.ly/AquiferSolverByExcel).

Final results (5 sheets)

• h: final results with the hydraulic heads in the aquifer [L]

• QNorth: flows through cell north boundaries [L$^3$T$^{-1}$]

• QSouth: flows through cell south boundaries [L$^3$T$^{-1}$]

• QWest: flows through cell west boundaries [L$^3$T$^{-1}$]

• QEast: flows through cell east boundaries [L$^3$T$^{-1}$]

Input parameters (8 sheets)

• i: active cells

• hfix: prescribed heads [L]

• T: transmissivities [L$^2$T$^{-1}$]

• W: pumping well extraction [L$^3$T$^{-1}$] (negative if injection)

• QN: infiltration flow [L$^3$T$^{-1}$]

• hR: river stage [L]

• hB: elevation of riverbed bottom [L]

• R: riverbed conductance [L$^2$T$^{-1}$]

Intermediate variables (6 sheets)

• TN: Transmissivity at the interface with the north cell [L$^2$T$^{-1}$] computed as the harmonic average of adjacent transmissivities

• TS: Transmissivity at the interface with the south cell [L$^2$T$^{-1}$]

• TW: Transmissivity at the interface with the west cell [L$^2$T$^{-1}$]

• TE: Transmissivity at the interface with the east cell [L$^2$T$^{-1}$]

• TT: Sum of TN, TS, TW and TE

• Qriv: River recharge flow [L$^3$T$^{-1}$]

Each spreadsheet shows a spatial representation of the respective variable.

The user must choose a consistent set of units to describe each of the input parameters; the intermediate results and the final results will be in consonance with that decision. In the example shown herein, meters and days have been chosen as the basic units to represent all variables.

The setup of this workbook follows the subsequent four steps:

Step 0. Create workbook. Create a new workbook. Go to calculation preferences and enable iterative calculation. This is necessary because, when Eq. (15) is introduced in all active cells, there is an error of circular references since the value of each cell depends on the cell values of all adjacent cells, and vice versa. This error disappears when iterative calculations are enabled and the spreadsheet is allowed to keep iterating until the circular references are satisfied. When to stop the iterations is controlled by two parameters that have to be defined in the calculation preferences panel: the maximum number of iterations and the maximum change between iterations (for the solution of the groundwater flow equation, start with 10,000 iterations and a maximum change of 10$^{-5}$). Save the first five columns for annotations; the model will be implemented starting at column F. Modify the row heights and the column widths starting at column F to create a square mesh (good values are row height equal to 30, column width equal to 5); name this sheet h. Create 18 copies of the first sheet and name them i, hfix, T, W, QN, hR, hB, R, TN, TS, TW, TE, TT, Qriv, QNorth, QSouth, QWest and QEast.

Step 1. Define active cells and cells with prescribed heads. Move to sheet i, select 19 rows by 33 columns starting at cell I5 and mark a thick contour—this will be the enclosing rectangle of the aquifer. This rectangle is impermeable; no water will enter or exit it. Next, mark with 1s the active cells of the aquifer and with 0s the inactive cells, according to the discretization of Fig. 2. Figure 4 shows this sheet; it has been conditionally formatted to highlight the active part of the aquifer (to conditionally format a range of cells, select the range and then go to menu Format and choose item Conditional Formatting); also, row and column numbers have been added for reference, although they play no role in the calculations. This sheet is particularly important since it defines on which cells computations will be performed; its layout should coincide with the layouts in the rest of the sheets containing the input parameters. Before starting to fill the rest of the parameters, it is convenient to copy this layout to the rest of the sheets and position the enclosing rectangle starting at I5.

Besides the active cells, it is necessary to indicate the cells with prescribed heads and their prescribed head values. These values are specified in sheet hfix; the rectangle enclosing the aquifer in that sheet should contain empty cells (with no values) except for those cells with prescribed heads, where the prescribed head values are specified. Figure 5 shows sheet hfix; in this example, the prescribed heads coincide with the water elevation at the lake (100 m) on those cells where the lake connects to the aquifer.

Fig. 4

Sheet with active cells

Fig. 5

Sheet with prescribed head cells and their values

Step 2. Input data. The next step consists in filling up the data in the corresponding spreadsheets, keeping the same layout for all sheets. In sheet T, transmissivity values are introduced. In this case, since there are three zones of transmissivity, three named variables are defined in the first columns of the sheet and the values are introduced making reference to these variables. Using named variables, it will be easy to see the aquifer response to changes in the zone values by only acting in the variables defined on the left. Figure 6 shows the T sheet; the named variables are placed in the buffer columns at the left of the sheet; the values chosen for the three zones are 1,000, 2,000 and 500 m$^2$ day$^{-1}$. (Refer to the Excel user manual on how to define a named range; in this case, the named range is a single cell to which a name is attached, then the names are used to fill in the cell values within the aquifer). In sheet W, the three well rates are introduced using named cells on the left side of the sheet. Figure 7 shows the W sheet; the values chosen are 10,000, 20,000 and 5,000 m$^3$ day$^{-1}$. In sheet QN, the input flow as leaky infiltration is given; in this case, only one infiltration zone is defined over all the active cells. On the left side of the sheet, two variables have been defined, one with the infiltration rate N and the other with the cell size $\varDelta$. The active cells already contain the product $N\varDelta ^2$, which is the infiltration flow. Figure 8 shows the QN sheet; the infiltration rate chosen is 0.0001 m day$^{-1}$, and the cell size 100 m. The next and final three spreadsheets include the river parameters along the discretized version of the river according to Fig. 2. Figure 9 shows the three sheets with the river parameters: river stage, riverbed bottom and conductance; the river flows from north to south with a mild slope of about 0.1%; a conductance value of 50 m$^2$ day$^{-1}$ results for a riverbed with a conductivity of 10$^{-2}$ m day$^{-1}$, a riverbed thickness of 1 m and an intersecting area of 5000 m$^2$. (In all these sheets, the 0 values at the inactive cells are kept to highlight the contour of the aquifer; they will not have any influence in the final results, since being on inactive cells do not enter into the computations.)

Fig. 6

Sheet with transmissivity values

Fig. 7

Sheet with extraction wells

Fig. 8

Sheet with infiltration rates

Fig. 9

Sheets with river parameters

Step 3. Compute intermediate variables. Now, it is time to compute the intermediate variables $T_N', T_S', T_W'$ and $T_E'$ that appear in (15). A unique expression is written that takes into account whether or not a cell is fully surrounded by active cells; if it is not, some of these values must be set to zero. The expression used to compute the north interblock transmissivity for cell I5 at the upper left corner of the rectangle enclosing the aquifer is

This expression reads as follows:

• If the current cell is inactive, leave $T'_N$ as an empty string; otherwise

  • If the current cell is active and the adjacent cell to the north is inactive, then set $T'_N$ to zero; otherwise

    • Set $T'_N$ equal to the harmonic mean of the two adjacent cells.

This expression is copied within the range I5:AO23 enclosing the aquifer.

Similar expressions are written for the other three interblock transmissivities. The values of the intercell transmissivities are computed once at the beginning and do not change during the iterative solution of the equation.

The resulting interblock transmissivity values can be seen in Fig. 10. In addition, to speed up the calculations, sheet TT is constructed with the sum of $T_N', T_S', T_W'$ and $T_E'$, which appears in the denominator of Eq. (15).

Fig. 10

Sheets with interblock conductivities. The zero values along the north, south, west and east borders indicate which are $T_N', T_S', T_W'$ and $T_E'$

Another intermediate variable is the flow entering from the river, $Q_{Riv}$. This intermediate variable will be recomputed at each iteration since it depends on the value of the piezometric head at the current cell. As the spreadsheet iterates, the computed piezometric heads get updated and so is the exchange flow with the river. The expression to compute the river inflow to the aquifer for cell I5 is

This expression reads as follows:

• If the current cell is inactive, leave $Q_{Riv}$ as an empty string; otherwise

  • If the piezometric head at the current cell is below the bottom of the riverbed then use the second line in Eq. (14) to compute the flow into the aquifer; otherwise

    • Use the first line in Eq. (14) to compute the flow into the aquifer.

Step 4. Iterative solution for piezometric heads. Since there are multiple circular references for the expressions of the head at any given cell as a function of the surrounding cells, the spreadsheet uses iterative calculations to find the values of the piezometric heads satisfying the expression given by (15). There are three named variables on the left of the sheet that control the calculations. Since calculations are iterative, there is a need to first initialize the active cells with some initial guess value; variables Restart and hini control this initialization; when Restart is positive, all active cells are set to the initial value hini. When Restart is zero, then calculations begin. There is a third variable, hundef, with an easily identifiable value to be given to the inactive cells within the rectangular range enclosing the aquifer; in this case the value chosen is $-99$. With these considerations, the expression for the piezometric at cell I5 is

This expression reads as follows:

• If the current cell is inactive, set the piezometric head to value hundef; otherwise

  • If the cell corresponds to a prescribed head cell, set the piezometric head equal to the prescribed head value; otherwise

    • If the Restart flag is set to a value larger than zero, initialize the cell with the value hini; otherwise

      • Compute the piezometric head using Eq. (15).

Because of the way Excel treats empty cells, a VALUE! error may appear when the head expression is populated within the aquifer range. If this happens, there are two quick and easy fixes. The first one is to add a ring of zeros (inactive cells) around the rectangle enclosing the aquifer in sheet i. The second one is to add a ring of zeros around the rectangle enclosing the aquifer in sheet h. To remove the VALUE! errors and try again, the only thing needed is to set the Restart flag to a number larger than zero, thus reinitializing the heads within the aquifer domain. If the second option is chosen, the ring of zeros can be removed once the VALUE! error has disappeared.

Once all input data have been entered, the intermediate spreadsheets constructed, and the piezometric head sheet populated with the last expression, the solution is obtained by first setting an initial head value to start the iterative calculations (this is done by setting the Restart flag to a positive value and variable hini to the initial head value) followed by setting the restart flag to zero, which launches the calculations. Iterative calculations in Excel use a Gauss–Seidel-like iterative approach (Fetter 2014, p. 522); Excel will perform as many iterations as indicated in Step 0 or until the changes from one iteration to the next in the piezometric head values are below the tolerance also set in Step 0. On some occasions, these number of iterations may not be enough and a new batch should be run; hitting F9 or clicking on the Calculate label at the bottom of the spreadsheet edge will trigger a new run. When the number of iterations is small or the tolerance large, it will be apparent to the user how the heads change from one iteration batch to another. Convergence is achieved only when these changes are unnoticeable.

Figure 11 shows the resulting piezometric heads for the input parameters described before. The same Excel worksheet can generate a surface plot like the one in Fig. 12, where the cones of depression induced by the wells can be seen and also the steep gradient next to the lake induced by the low transmissivity zone in the eastern part of the aquifer. To produce such a plot in Excel, simply select the range containing the aquifer heads (h!I5:h!AO23, in the example), and then choose to insert a Surface Chart.

Fig. 11

Piezometric head solution of the groundwater flow problem for the parameters shown in the previous figures

Fig. 12

Surface rendering of the piezometric head solution by Excel shown in the previous figure

A global balance is a convenient tool to check the goodness of the solution. To compute it, first, it is necessary to evaluate all cell-to-cell flows. For this purpose, the spreadsheets QNorth, QSouth, QWest and QEast are constructed evaluating the expressions in Eqs. (234)–(5). As an example, the expression for QNorth at cell I5 is

This expression reads as follows:

• If the current cell is inactive leave QNorth as an empty string; otherwise

  • If the current cell is active and the adjacent cell to the north is inactive, then set QNorth to zero; otherwise

    • Set QNorth equal to expression (234).

Similar expressions are written for the flows entering the cell through the other three faces.

The components of the flow balance, reported on sheet h in the example, will be (i) the input through the wells computed as the negative sum of all values in sheet W within the aquifer range; (ii) the input by infiltration computed as the sum of all values in sheet QN within the aquifer range; (iii) the input through the river computed as the sum of all values in sheet Qriv within the aquifer range; and (iv) the input through the prescribed head cells computed as the negative sum of all the inputs to the prescribed head cells; this last sum is obtained using the SUMIF command in Excel as follows

where each summand in this expression is the summation of the fluxes in the QNorth, QSouth, QWest and QEast spreadsheets but only for those cells in which the prescribed head value in sheet hfix is larger than variable hundef, that is, only for the prescribed head cells. The total will be the flow going into the prescribed head cells; therefore, the negative sum will be the flow going from the prescribed head cells into the aquifer.

The sum of all four components should be equal or close to zero.

In the particular example shown here, the input through wells is −35,000 m$^{3}$ day$^{-1}$, the input by infiltration is 5070 m$^{3}$ day$^{-1}$, the river is hanging over the aquifer and loses 4435 m$^{3}$ day$^{-1}$ and the input from the lake is 25,645 m$^{3}$ day$^{-1}$. The sum of all these inputs should be zero but is 150 m$^{3}$ day$^{-1}$, which amounts to a 0.4% of the total extractions, a very small error.

4 Examples

Once the model is set up, it is very simple to demonstrate how changing different parameters will influence the final solution. Just for the sake of illustration, two examples are shown. Figure 13 shows the piezometric head distribution under the same stresses but with the low transmissivity zone T3 increased from 500 to 1500 m$^2$ day$^{-1}$. Note that the color scale has changed and that the gradient on the eastern side is much smaller. Figure 14 shows the piezometric head distribution under the same stresses and transmissivities as in the previous example, but assuming that the west border is also in contact with a lake that prescribes the head along the first column at 100 m. Notice that the color scale has changed again, and that the gradients are even smaller; also, checking spreadsheet Qriv, it is found that the river becomes a gaining river in its southern section and, overall, it gains more than it loses.

Another interesting exercise is to see how the iterative solution progresses. By reducing the maximum number of iterations in the preferences to 100, the spreadsheet can be commanded to keep iterating by asking to calculate again (by hitting F9). In this way it can be seen how the solution converges to the solution found when 10,000 iterations are set as the maximum value. The sensitivity of the final solution to the tolerance is another exercise worth doing, one might think that a tolerance of 1 cm could be enough, but testing such value will show that the iterations stop very far from the solution obtained when a tolerance of 10${^{-6}}$ m is used.

Fig. 13

New solution after increasing the transmissivity of zone 3 from 500 to 1,500 m$^2$ day$^{-1}$

Fig. 14

New solution after increasing the transmissivity of zone 3 from 500 to 1,500 m$^2$ day$^{-1}$ and setting the western boundary to a prescribed head value of 100 m, the same as the lake in the opposite side

5 Possible Extensions

The example described here has been done for steady-state flow in a vertically integrated confined aquifer. It will not be too difficult to extend the results for an unconfined aquifer, in which case, transmissivity would not be an input parameter but rather computed as the product of conductivity (a new input parameter) and saturated thickness given by the difference of piezometric head and aquifer bottom elevation (another new input parameter).

Trying to go multilayer will be tedious but possible. The simplest approach is to have all layers in each spreadsheet, for instance, for an aquifer like the one in the example but with three layers; the upper layer would be placed in rows 5 to 23, the middle layer in rows 25 to 43, and the bottom layer in rows 45 to 63. Expression (1) will be changed to include the input flows from the top and bottom cells, which will modify the expression for h.

Trying to model transient flow will not be difficult to implement for a single time step. It will be necessary to input initial heads and storage coefficient values. Implementing multiple time steps with time varying pumping, recharge, prescribed heads or river stages would be very complicated.

Finally, inverse modeling would be possible using Excel solver, which can be requested to identify, for instance, the value of T1 in the example that yields a head distribution that matches a number of observations.

6 Conclusions

Spreadsheets provide an easy and understandable way to implement sophisticated groundwater flow models. They can be used to teach the non-programmer student how to construct an aquifer numerical model with the simple combination of spreadsheets in which input data are collected and intermediate variables computed. The construction of such a model is, certainly, much faster than writing a dedicated computer program, with the added advantage that Excel already provides numerous graphical tools to display the results. The final results can be post-processed to evaluate, for instance, specific components of the flow balance and to check for the residual error incurred by the iterative solution of the equation. Once the model is constructed, it is very simple and very interactive to modify specific parameters and make scenario analysis, such as the impact of diminished infiltration due to climate change, or the impact that lowering the water levels in a connected lake may have. It would also be very simple to include further external flows, such as those due to evapotranspiration, drains or springs, or to modify the main expression (15) to account for rectangular cells or for transmissivity anisotropy.