1 Introduction

Stochastic simulation methods are used to quantify the spatial uncertainty and variability of pertinent attributes of natural phenomena in geosciences and geoengineering. Initial simulation methods were based on Gaussian assumptions and second-order statistics of corresponding random field models (Journel and Huijbregts 1978; David 1988; Goovaerts 1997). To address the limits of such Gaussian approaches, multiple point statistics (MPS)-based simulation methods were introduced (Guardiano and Srivastava 1993; Strebelle 2002; Zhang et al. 2006; Arpat and Caers 2007; Remy et al. 2009; Mariethoz et al. 2010; Mariethoz and Caers 2014; Mustapha et al. 2014; Chatterjee et al. 2016; Li et al. 2016; Zhang et al. 2017) to remove distributional assumptions, as well as to enable the reproduction of complex curvilinear and other geologic features by replacing the random field model with a framework built upon extraction of multiple point patterns from a training image (TI) or geological analogue. The main limitations of MPS methods are that they do not explicitly account for high-order statistics, nor do they provide consistent mathematical models as they generate TI-driven realizations. Previous studies have shown resulting realizations that comply with the TI used but do not necessarily reproduce the spatial statistics inferred from the data (Osterholt and Dimitrakopoulos 2007; Goodfellow et al. 2012). As an alternative, to address the above limitations, a high-order simulation (HOSIM) framework has been proposed as a natural generalization of the second-order-based random field paradigm (Dimitrakopoulos et al. 2010; Mustapha and Dimitrakopoulos 2010a, b, 2011; Minniakhmetov and Dimitrakopoulos 2017a, b; Minniakhmetov et al. 2018; Yao et al. 2018). The HOSIM framework does not make any assumptions about the data distribution, and the resulting realizations reproduce the high-order spatial statistics of the data. Similar to the MPS and most Gaussian simulation approaches, HOSIM methods generate realizations at the point support scale, whereas in most major areas of application, simulated realizations must be at the block support scale. Typically, the change of support scale needed is addressed by generating simulated realizations on a very dense grid of nodes that is then postprocessed to generate realizations at the block support size needed. This is a computationally demanding process, as related configurations may require extremely dense grids with on the order of many millions to billions of nodes. Thus, there is a need for computationally efficient methods that simulate directly at the block support scale.

In the context of conventional second-order geostatistics, direct block support simulation has been proposed. An approach termed “direct block simulation” was presented by Godoy (2003), which discretizes each block into several internal nodes, but only stores a single block value in memory for the next group simulation. This mechanism drastically reduces the amount of data stored in memory and saves considerable computational effort. The sequential direct block simulation method was expanded by Boucher and Dimitrakopoulos (2009) to incorporate multiple correlated variables by applying min/max autocorrelation factors. An explicit change of the support model and direct simulation at block support scale were used by Emery (2009). Although efficient, these methods carry all the limitations of a Gaussian simulation framework, and the related spatial connectivity is limited to two-point spatial statistics, thus they remain unable to characterize non-Gaussian variables, complex nonlinear geological geometries, and the critically important connectivity of extreme values (Journel 2018). Alternatives are, therefore, needed.

High-order sequential simulation methods use high-order spatial cumulants to describe complex geologic configurations and high-order connectivity. At the same time, simulated realizations remain consistent with respect to the statistics of the available data, while capitalizing on the additional information that TIs can provide. These high-order spatial cumulants are described by Dimitrakopoulos et al. (2010) as combinations of moment statistical parameters. A high-order simulation algorithm was proposed by Mustapha and Dimitrakopoulos (2010a), where the conditional probability density functions (cpdf) are approximated by Legendre polynomials and high-order spatial cumulants. A template is defined based on the central node to be simulated and the nearest conditioning data. The replicates of this configuration are obtained from both the data and TI, and are used as input for the calculation of the Legendre coefficients in the cpdf approximation. Advantages of this method lie in the absence of assumptions on the distribution of the data and in being a data-driven approach. The Legendre polynomial was replaced by Legendre-like splines as the basis function for the estimation of conditional probabilities by Minniakhmetov et al. (2018). Results show a more stable approximation of the related cpdf. Improving upon the computational performance, Yao et al. (2018) proposed a new approach, where the calculation of the cpdf is simplified and no explicit calculation of cumulants is required. Although effective, the methods described above are performed at point support scale.

This paper presents a new method that generates high-order stochastic simulations directly at the block support scale. The technique considers overlapping grids representing a study area at two support scales, viz. point and block, where the simulation process is implemented at the latter. In the sequential simulation process followed, only the initial point support data and previously simulated blocks are added to the set of conditioning values, thus drastically reducing the number of elements stored in memory. The block to be simulated and the nearest conditioning data, at the point or block support scale, define the spatial configuration of the template used. Similarly, the TI is represented at both support scales to provide replicates of related spatial template configurations. The conditional cross-support joint density function estimated at each block is approximated by Legendre-like splines.

The remainder of the paper is organized as follows: First, the proposed model for high-order block support simulation is presented. Subsequently, a case study in a controlled environment assesses the performance of the current approach. Next, the method is applied to an actual gold deposit to demonstrate its practical aspects. Conclusions follow.

2 High-Order Block Support Simulation

2.1 Sequential Simulation

In the following description, the index \( V \) relates to elements at the block support, while \( P \) represents point support. Consider a stationary and ergodic non-Gaussian random field (RF) \( Z_{P} \left( {u_{j} } \right) \) in \( R^{n} \), where \( u_{j} \) defines the location of nodes j in the domain \( D \subseteq R^{n} . \) Now, consider a transformation function that takes the above point support RF to the block support RF. Any upscaling function can be applied, but assume Eq. (1) for simplicity

$$ Z_{V} \left( v \right) = \frac{1}{\left| V \right|}\int\limits_{{u_{j} \in \, v}} {Z_{P} \left( {u_{j} } \right){\text{d}}u_{j} } . $$
(1)

\( Z_{V} \left( {v_{i} } \right) \) is also a RF, indexed as \( v_{i} \in D \subseteq R^{n} ,i = 1, \ldots ,N_{V}, \) where \( N_{V} \) represents the total number of blocks to be simulated within the domain \( D \subseteq R^{n} \). \( Z_{V} \left( {v_{i} } \right) \) is the upscaled RF from \( Z_{P} (u_{j} ) \) considering all nodes \( u_{j} \) that are discretized within the block centered in \( v_{i} \), where V is the volume.

The outcomes from the above RFs are denoted as \( z_{j}^{P} = z_{P} \left( {u_{j} } \right) \) and \( z_{i}^{V} = z_{V} \left( {v_{i} } \right) \), respectively, for the point and block support RF \( Z_{P} \left( {u_{j} } \right) = Z_{j}^{P} \) and \( Z_{V} \left( {v_{i} } \right) = Z_{i}^{V} \). Herein, the objective is to simulate a realization of the RF \( Z_{i}^{V} \) given the set of initial conditioning values at point support scale denoted as \( d_{p} = \left\{ {z_{1}^{P} , \ldots ,z_{{N_{P} }}^{P} } \right\} \), \( N_{P} \) being the total of the conditioning point support values. According to the sequential simulation theory in the geostatistical field, the joint probability density function (jpdf) \( f_{{Z_{1}^{V} , \ldots ,Z_{k}^{V} }} \) can be decomposed into the products of the respective univariate distributions (Johnson 1987; Journel and Alabert 1989; Journel 1994; Goovaerts 1997; Dimitrakopoulos and Luo 2004)

$$ \begin{aligned} & f_{{_{{Z_{1}^{V} , \ldots ,Z_{{N_{V} }}^{V} }} }} \left( {z_{1}^{V} ,z_{2}^{V} , \ldots ,z_{{N_{V} }}^{V} \left| {d_{P} } \right.} \right) = f_{{Z_{1}^{V} }} \left( {z_{1}^{V} \left| {d_{P} } \right.} \right)f_{{Z_{2}^{V} , \ldots ,Z_{{N_{V} }}^{V} }} \left( {z_{2}^{V} , \ldots ,z_{{N_{V} }}^{V} \left| {d_{P} ,z_{1}^{V} } \right.} \right) \\ & \qquad = f_{{Z_{1}^{V} }} \left( {z_{1}^{V} \left| {d_{P} } \right.} \right)f_{{Z_{2}^{V} }} \left( {z_{2}^{V} \left| {d_{P} ,z_{1}^{V} } \right.} \right) \ldots f_{{Z_{{N_{V} }}^{V} }} \left( {z_{{N_{V} }}^{V} \left| {d_{P} ,z_{1}^{V} ,z_{2}^{V} , \ldots ,z_{{N_{V} - 1}}^{V} } \right.} \right). \\ \end{aligned} $$
(2)

According to Eq. (2), each block \( v^{k} \) is simulated based on the estimation of the conditional cross-support probability density function \( f_{{Z_{k}^{V} }} \left( {z_{k}^{{_{V} }} \left| {d_{P} ,z_{1}^{V} ,z_{2}^{V} , \ldots ,z_{k - 1}^{V} } \right.} \right) \), which according to Bayes’ rule (Stuart and Ord 1987) is

$$ f_{{Z_{k}^{V} }} \left( {z_{k}^{{_{V} }} \left| {d_{P} ,z_{1}^{V} ,z_{2}^{V} , \ldots ,z_{k - 1}^{V} } \right.} \right) = \frac{{f_{\text{Z}} \left( {d_{P} ,z_{1}^{V} ,z_{2}^{V} , \ldots ,z_{k - 1}^{V} ,z_{k}^{{_{V} }} } \right)}}{{\int\limits_{D} {f_{\text{Z}} \left( {d_{P} ,z_{1}^{V} ,z_{2}^{V} , \ldots ,z_{k - 1}^{V} ,z_{k}^{{_{V} }} } \right)dv_{k} } }}, $$
(3)

where \( {\text{Z}} = Z_{1}^{P} , \ldots ,Z_{{N_{P} }}^{P} ,Z_{1}^{V} , \ldots ,Z_{k}^{V} \). It is sufficient to approximate only the cross-support joint probability density function \( f_{\text{Z}} \left( {d_{P} ,z_{1}^{V} ,z_{2}^{V} , \ldots ,z_{k - 1}^{V} ,z_{k}^{{_{V} }} } \right) \). In this paper, this cross-support joint probability density function is approximated using Legendre-like orthogonal splines (Wei et al. 2013; Minniakhmetov et al. 2018).

2.2 Joint Probability Density Function Approximation

For simplicity, let \( f\left( z \right) \) be the pdf of a random variable \( Z \) defined in \( \varOmega = \left[ {a,b} \right] \) and let \( \varphi_{1} \left( z \right),\varphi_{2} \left( z \right), \ldots \) be a set of orthogonal functions defined in the same space \( \varOmega \). Then, a fixed number \( \omega \) of those orthogonal functions can approximate \( f\left( z \right) \) (Lebedev 1965; Mustapha and Dimitrakopoulos 2010a; Minniakhmetov et al. 2018; Yao et al. 2018), when multiplied by the coefficients \( L_{i} \)

$$ f\left( z \right) \approx \sum\limits_{i = 0}^{\omega } {L_{i} \varphi_{i} \left( z \right)} . $$
(4)

Since the sets of functions are orthogonal

$$ \int\limits_{a}^{b} {\varphi_{i} \left( z \right)\varphi_{j} \left( z \right)} {\text{d}}z = \delta_{ij} , $$
(5)

where \( \delta_{ij} \) is the Kronecker delta indexed by \( i \) and \( j \), such that it take a unitary value if \( i = j \) and 0 otherwise, using the definition of the expected value of one for a basis function

$$ E\left[ {\varphi_{i} \left( z \right)} \right] = \int\limits_{a}^{b} {\varphi_{i} \left( z \right)f\left( z \right)} {\text{d}}z. $$
(6)

Replacing \( f\left( z \right) \) as in Eq. (4) yields

$$ \begin{aligned} & E\left[ {\varphi_{i} \left( z \right)} \right] \approx \int\limits_{a}^{b} {\varphi_{i} \left( z \right)\sum\limits_{j = 0}^{\omega } {L_{j} \varphi_{j} \left( z \right)} {\text{d}}z} = \sum\limits_{j = 0}^{\omega } {L_{j} \int\limits_{a}^{b} {\varphi_{j} \left( z \right)\varphi_{i} \left( z \right){\text{d}}z} } \\ & \quad = \sum\limits_{j = 0}^{\omega } {L_{j} \delta_{ij} } = L_{i} . \\ \end{aligned} $$
(7)

The coefficient \( L_{i} \) can be obtained experimentally from an available sample, thus \( f\left( z \right) \) is approximated by Eq. (4).

Moving to the multivariate cross-support case, at every block location \( v^{k} \) the cross-support jpdf \( f_{\text{Z}} \left( {d_{P} ,z_{1}^{V} ,z_{2}^{V} , \ldots ,z_{k - 1}^{V} ,z_{k}^{V} } \right) \) can be defined in a similar sense. Considering in practice that not all the samples are included as conditioning, \( n_{V} \) and \( n_{P} \) are the maximum number of elements at block support and point support scale, respectively, in the calculation. Hereinafter, the above cross-support jpdf is referred to as \( f\left( {z_{0}^{V} , \ldots ,z_{{n_{V} }}^{V} ,z_{1}^{P} , \ldots ,z_{{n_{P} }}^{P} } \right) \) to simplify the notation and ensure better understanding of the variables in both the block and point support layers. Also note that, without loss of generality, \( z_{0}^{V} \) is the value to be simulated at location \( v_{0} \). The cross-support jpdf is defined in the domain \( \left[ {a,b} \right]^{{n_{V} + 1}} \times \left[ {a,b} \right]^{{n_{P} }} \). Note that the interval for the block support is not necessarily the same as for the point support. This also applies to the basis functions \( \varphi_{j} \left( z \right) \), which could be discretized differently for both supports. Similarly to the univariate case, the cross-support jpdf can be approximated as

$$\begin{aligned}& f\left( {z_{0}^{V} , \ldots ,z_{{n_{V} }}^{V} ,z_{1}^{P} , \ldots ,z_{{n_{P} }}^{P} } \right) \approx \sum\limits_{{k_{0}^{V} }}^{\omega } \ldots \sum\limits_{{k_{V}^{{n_{V} }} }}^{\omega } \sum\limits_{{k_{P}^{1} }}^{\omega } \ldots \sum\limits_{{k_{P}^{{n_{P} }} }}^{\omega } \left[ L_{{k_{0}^{V} \ldots k_{{n_{V} }}^{V} k_{1}^{P} \ldots k_{{n_{P} }}^{P} }} \varphi_{{k_{0}^{V} }} \left( {z_{0}^{V} } \right) \right.\\ &\left. \quad \ldots \varphi_{{k_{{n_{V} }}^{V} }} \left( {z_{{n_{V} }}^{V} } \right)\varphi_{{k_{1}^{P} }} \left( {z_{1}^{P} } \right) \ldots \varphi_{{k_{{n_{P} }}^{P} }} \left( {z_{{n_{P} }}^{P} } \right) \right] .\end{aligned} $$
(8)

The coefficients \( L_{i \ldots jk \ldots l} \) can be calculated experimentally, since they can be obtained from the orthogonality property of the basis functions. Following the definition of the expected value of a basis function, this is expressed as

$$ \begin{aligned} & E\left[ {\varphi_{i} \left( {z_{0}^{V} } \right) \ldots \varphi_{j} \left( {z_{{n_{V} }}^{V} } \right)\varphi_{k} \left( {z_{1}^{P} } \right) \ldots \varphi_{l} \left( {z_{{n_{P} }}^{P} } \right)} \right] \\ & \quad = \int\limits_{a}^{b} { \ldots \int\limits_{a}^{b} {\int\limits_{a}^{b} { \ldots \int\limits_{a}^{b} {\varphi_{i} \left( {z_{0}^{V} } \right) \ldots \varphi_{j} \left( {z_{{n_{V} }}^{V} } \right)\varphi_{k} \left( {z_{1}^{P} } \right)} } } } \\ & \qquad \ldots \varphi_{l} \left( {z_{{n_{P} }}^{P} } \right)f\left( {z_{0}^{V} , \ldots ,z_{{n_{V} }}^{V} ,z_{1}^{P} , \ldots ,z_{{n_{P} }}^{P} } \right){\text{d}}z_{0}^{V} \ldots {\text{d}}z_{{n_{V} }}^{V} {\text{d}}z_{1}^{P} \ldots {\text{d}}z_{{n_{P} }}^{P} . \\ \end{aligned} $$
(9)

Replacing \( f\left( {z_{V}^{0} , \ldots ,z_{V}^{{n_{V} }} ,z_{P}^{1} , \ldots ,z_{P}^{{n_{P} }} } \right) \) as in Eq. (8) yields

$$ \begin{aligned} & E\left[ {\varphi_{i} \left( {z_{0}^{V} } \right) \ldots \varphi_{j} \left( {z_{{n_{V} }}^{V} } \right)\varphi_{k} \left( {z_{1}^{P} } \right) \ldots \varphi_{l} \left( {z_{{n_{P} }}^{P} } \right)} \right] \\ & \quad \approx \int\limits_{a}^{b} { \ldots \int\limits_{a}^{b} {\int\limits_{a}^{b} { \ldots \int\limits_{a}^{b} {\varphi_{i} \left( {z_{0}^{V} } \right) \ldots \varphi_{j} \left( {z_{{n_{V} }}^{V} } \right)\varphi_{k} \left( {z_{1}^{P} } \right) \ldots \varphi_{l} \left( {z_{{n_{P} }}^{P} } \right)} } } } \\ & \qquad \times\sum\limits_{{k_{0}^{V} }}^{\omega } { \ldots \sum\limits_{{k_{{n_{V} }}^{V} }}^{\omega } {\sum\limits_{{k_{1}^{P} }}^{\omega } {} } }\ldots \sum\limits_{{k_{{n_{P} }}^{P} }}^{\omega } \left[ L_{{k_{0}^{V} \ldots k_{{n_{V} }}^{V} k_{1}^{P} \ldots k_{{n_{P} }}^{P} }} \varphi_{{k_{0}^{V} }} \left( {z_{0}^{V} } \right) \right.\\ &\qquad\left.\ldots \varphi_{{k_{{n_{V} }}^{V} }} \left( {z_{{n_{V} }}^{V} } \right)\varphi_{{k_{1}^{P} }} \left( {z_{1}^{P} } \right) \ldots \varphi_{{k_{{n_{P} }}^{P} }} \left( {z_{{n_{P} }}^{P} } \right)\right] {\text{d}}z_{0}^{V} \ldots {\text{d}}z_{{n_{V} }}^{V} {\text{d}}z_{1}^{P} \ldots {\text{d}}z_{{n_{P} }}^{P} \\ &\quad = \sum\limits_{{k_{0}^{V} }}^{\omega } { \ldots \sum\limits_{{k_{{n_{V} }}^{V} }}^{\omega } {\sum\limits_{{k_{1}^{P} }}^{\omega } { \ldots \sum\limits_{{k_{{n_{P} }}^{P} }}^{\omega } {\left[ {L_{{k_{0}^{V} \ldots k_{{n_{V} }}^{V} k_{1}^{P} \ldots k_{{n_{P} }}^{P} }} \int\limits_{a}^{b} { \ldots \int\limits_{a}^{b} {\int\limits_{a}^{b} { \ldots \int\limits_{a}^{b} {\varphi_{i} \left( {z_{0}^{V} } \right)\varphi_{{k_{0}^{V} }} \left( {z_{0}^{V} } \right)} } } } } \right.} } } } \\ & \left. {\qquad \ldots \varphi_{j} \left( {z_{{n_{V} }}^{V} } \right)\varphi_{{k_{V}^{{n_{V} }} }} \left( {z_{{n_{V} }}^{V} } \right)\varphi_{k} \left( {z_{1}^{P} } \right)\varphi_{{k_{P}^{1} }} \left( {z_{1}^{P} } \right) \ldots \varphi_{l} \left( {z_{{n_{P} }}^{P} } \right)\varphi_{{k_{{n_{P} }}^{P} }} \left( {z_{{n_{P} }}^{P} } \right)} \right]\\ &\qquad {\text{d}}z_{0}^{V} \ldots {\text{d}}z_{{n_{V} }}^{V} {\text{d}}z_{1}^{P} \ldots {\text{d}}z_{{n_{P} }}^{P} \\ & \quad = \sum\limits_{{k_{0}^{V} }}^{\omega } { \ldots \sum\limits_{{k_{{n_{V} }}^{V} }}^{\omega } {\sum\limits_{{k_{1}^{P} }}^{\omega } { \ldots \sum\limits_{{k_{{n_{P} }}^{P} }}^{\omega } {\left[ {L_{{k_{0}^{V} \ldots k_{{n_{V} }}^{V} k_{1}^{P} \ldots k_{{n_{P} }}^{P} }} \delta_{{i_{{k_{0}^{V} }} }} \ldots \delta_{{j_{{k_{{n_{V} }}^{V} }} }} \delta_{{k_{{k_{1}^{P} }} }} \delta_{{l_{{k_{{n_{P} }}^{P} }} }} } \right]} } } } = L_{i \ldots jk \ldots l} . \\ \end{aligned} $$
(10)

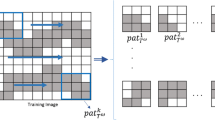
Now, to determine \( L_{i \ldots jk \ldots l} \), the expected value from Eq. (10) is calculated from replicates of the training image according to a template defined from the simulation grid and sampling data.

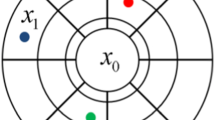
Let \( \tau = \left[ {v_{0} , \ldots ,v_{{n_{V} }} ,u_{1} , \ldots ,u_{{n_{P} }} } \right] \) be a template as in Fig. 1, where \( v_{0} \) and \( v_{1} \) represent locations of block support, and \( u_{1} ,u_{2}, {\text{ and }}u_{3} \) represent point support locations. \( v_{0} \) is the location of the block to be simulated, and \( n_{P} \) and \( n_{V} \) are, respectively, the total number of points and blocks used as conditioning. In the figure, the grids at point and block support scale appear separated, but this is for visualization purposes only. In reality, they overlap with each other, and the distance between the layers is set to 0. \( \tau \) is defined considering limited conditioning values, which are chosen in order of Euclidean proximity from the central block to be simulated. Having the specified template \( \tau \), the TI is scanned, and the replicates of such a template are retrieved. Note that \( \tau \) has elements that belong to the point and block support scales. Similarly, the TI must be available at both scales. Therefore, assuming a TI input at the point support scale, it is rescaled to block support scale, and both are retrieved during the simulation process, each in its respective layer.

Fig. 1
figure 1

Example template \( \tau \) with conditioning data capturing values at both point and block support scales

Full size image

The algorithm for the block support high-order simulation method is as follows:

  1. 1.

    Upscale the TI from point to block support scale.

  2. 2.

    Define a random path to visit all the unsampled block locations on the simulation grid.

  3. 3.

    At each \( v^{0} \) block location:

    1. (a)

      Find the nearest conditioning point and block support values.

    2. (b)

      Obtain the template \( \tau \) according to the configuration of the central block and related conditioning values at both support scales.

    3. (c)

      Scan the training images, searching for replicates of the template \( \tau \) and corresponding values.

    4. (d)

      Calculate all the spatial cross-support coefficients \( L_{i \ldots jk \ldots l} \) using Eq. (10).

    5. (e)

      Derive the conditional cross-support jpdf \( f_{{Z_{0}^{V} }} \left( {z_{0}^{V} \left| {d_{P} ,z_{1}^{V} ,z_{2}^{V} , \ldots ,z_{k}^{V} } \right.} \right) \) according to Eqs. (8) and (3).

    6. (f)

      Draw a uniform value from \( \left[ {0,1} \right] \) to sample \( z_{0}^{V} \) from the conditional cumulative distribution derived from the above.

    7. (g)

      Add \( z_{0}^{V} \) to the simulation grid at block support scale so that it can be a conditioning value for the next block.

  4. 4.

    Repeat steps 2 and 3 for additional realizations.

2.3 Approximation of a Joint Probability Density Using Legendre-Like Orthogonal Splines

The current paper uses Legendre-like splines (Wei et al. 2013; Minniakhmetov et al. 2018) as a means to obtain the basis function mentioned above. In short, those splines are a combination of Legendre polynomials (Lebedev 1965) up to order \( r \) and linear combinations of B-splines (de Boor 1978). B-splines are a particular class of piecewise polynomials (splines) connected by some condition of continuity, and by themselves do not form an orthogonal basis. Thus, as introduced in Wei et al. (2013), the first \( r \) +1 splines are the Legendre polynomials, which can be defined as (Lebedev 1965)

$$ \varphi_{r} = \frac{1}{{2^{r} r!}}\left( {\frac{{{\text{d}}^{r} }}{{{\text{d}}z^{r} }}} \right)\left[ {\left( {z^{2} - 1} \right)^{r} } \right],\quad - 1 \le z \le 1. $$
(11)

The additional functions are constructed given the domain

$$ T = \{ \underbrace {{a,a, \ldots ,t_{0} = a}}_{r + 1} < t_{1} \le t_{2} \le \ldots \le t_{{m_{\rm{max} } }} < \underbrace {{t_{{m_{\rm{max} } + 1}} = b,b, \ldots ,b}}_{r + 1}\} , $$
(12)

where the elements \( t_{i} \) are referred to as knots and \( m_{\rm{max} } \) represents the maximum number of knots; note that Minniakhmetov et al. (2018) present a study on how to choose \( m_{\hbox{max} } \) to obtain computationally stable polynomial approximations. The final Legendre-like splines are defined as

$$ \varphi_{r + m} (t) = \frac{{{\text{d}}^{r + 1} }}{{{\text{d}}t^{r + 1} }}f_{m} (t),\quad m = 1 \ldots m_{\rm{max} } . $$
(13)

\( f_{m} (t) \) is the determinant of the following matrix:

$$ f_{m} (t) = \det \left( {\begin{array}{*{20}c} {B_{ - r,2r + 1,m} (t)} & {B_{ - r + 1,2r + 1,m} (t)} & \cdots & {B_{ - r + m - 1,2r + 1,m} (t)} \\ {B_{ - r,2r + 1,m} (t_{1} )} & {B_{ - r + 1,2r + 1,m} (t_{1} )} & \vdots & {B_{ - r + m - 1,2r + 1,m} (t_{1} )} \\ \vdots & \vdots & \ddots & \vdots \\ {B_{ - r,2r + 1,m} (t_{m - 1} )} & {B_{ - r + 1,2r + 1,m} (t_{m - 1} )} & \cdots & {B_{ - r + m - 1,2r + 1,m} (t_{m - 1} )} \\ \end{array} } \right), $$
(14)

which is constructed from the auxiliary splines \( B_{i,r,m} \left( t \right) \) of order \( r \), obtained according to the recursive rule

$$ \begin{aligned} & B_{i,0,m} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & \quad{t_{i,m} \le t \le t_{i + 1,m} } \hfill \\ {0,} \hfill & \quad{\text{otherwise}} \hfill \\ \end{array} } \right., \\ & B_{i,r,m} \left( t \right) = \frac{{t - t_{i,m} }}{{t_{i + r - 1,m} - t_{i,m} }}B_{i,r - 1,m} \left( t \right) + \frac{{t_{i + r,m} - t}}{{t_{i + r,m} - t_{i + 1,m} }}B_{i + 1,r - 1,m} \left( t \right). \\ \end{aligned} $$
(15)

These auxiliary functions are defined on the knot sequence \( T_{m} = \left\{ {t_{i,m} } \right\}_{i = - r}^{r + m + 1} \), \( m = 1 \ldots \)\( m_{\rm{max} } - 1 \), and the term \( t_{i,m} \) is defined as

$$ t_{i,m} = \left\{ {\begin{array}{*{20}l} {a,} \hfill &\quad { - r \le i \le 0} \hfill \\ {t_{i} ,} \hfill &\quad { 1\le i \le m} \hfill \\ {b,} \hfill &\quad {m + 1 \le i \le m + r + 1} \hfill \\ \end{array} } \right.. $$
(16)

3 Testing with an Exhaustive Dataset

The method outlined above is tested using the two-dimensional image of the Walker Lake dataset (Isaaks and Srivastava 1989). This exhaustive dataset comprises two correlated variables U and V with sizes of 260 × 300 pixels. Random stratified sampling is used to retrieve 234 values from or 0.3 % of the exhaustive image V to be used as the dataset in the direct block simulation of V, to test the proposed method. The full dataset V is converted from the point to a block support representation by averaging over 5 × 5 pixels. This block support version is referred to here as the fully known reference image and is used for comparisons. Figure 2 shows V at the point and block support scale, as well as the dataset to be used. The image U is chosen as the training image in the simulation process. Figure 3 presents the TI at both point and block support (5 × 5 unit size) scales. To help the method find more meaningful spatial patterns of the potential conditioning templates, the histogram of the TI is matched to that of the dataset. Histograms of the exhaustively known image, TI, and dataset are displayed in Fig. 4, and basic statistics are presented in Table 1.

Fig. 2
figure 2

Exhaustive image Va at point support scale, b at block support scale, and c 234 samples from the image in a

Full size image
Fig. 3
figure 3

Training image U at a point support scale and b block support scale

Full size image
Fig. 4
figure 4

Histogram of data, reference, and training image at point support scale

Full size image
Table 1 Basic statistics of dataset, training image, and fully known image at point support scale
Full size table

The test conducted consists of generating 15 simulated realizations of the V dataset at block support scale, using the data and the training image mentioned above. Note that the maximum number of knots used (Eq. 12) is 50, which provides computationally efficient and stable polynomial approximations, as appropriate. Figure 5 shows three of the simulated realizations generated, and Table 2 presents the statistics related to the average of the 15 simulations, training image, and reference image at block scale. Comparison of Figs. 2b and 5 suggests that the simulations reproduce the main structures of low and high values of the fully known reference image V. The histograms and variograms presented in Figs. 6 and 7 reasonably follow the behavior exhibited by the variogram model from the data and training image, respectively. Note that the variograms of the data are computed at point scale and rescaled to represent the corresponding volume–variance relation (Journel and Huijbregts 1978).

Fig. 5
figure 5

Three example simulated realizations of the Walker Lake reference image V

Full size image
Table 2 Basic statistics of the average of the simulations, training image, and reference image at block support scale
Full size table
Fig. 6
figure 6

Histograms of the simulations at block support scale, and comparison with reference and training image also at block support scale

Full size image
Fig. 7
figure 7

Variograms of simulated realizations, exhaustive image, TI, and variogram from data rescaled to block support variance: a WE direction, and b NS direction

Full size image

Spatial cumulants (Dimitrakopoulos et al. 2010) can quantify the spatial relationships between three and more points and are used herein to assess high-order spatial patterns. The third-order cumulant maps are presented along with the template used for its calculation in Fig. 8. Figure 9 shows the fourth-order cumulant map, where three slices of the complete cumulant map and the related template are displayed. In both figures, the color ranges from blue to red, representing lower to higher spatial intercorrelation between values. Note that the reference and training image high-order maps are calculated on block support scale, while the cumulant maps related to each simulation are averaged to a single map using the 15 stochastic simulated realizations at block support scale. During the calculation of the high-order spatial statistics from the data, only a few replicates are obtained and Fig. 8a presents a smooth interpolation using B-splines. Regarding the third-order maps, the average of the simulations match the spatial features observed in the data and fully known dataset. It also shares similarities with the third-order cumulants map from TI; this is somewhat expected as the process captures high-order relations from the TI at block support scale at well. These spatial relations present in the TI end up being present in the realizations as well.

Fig. 8
figure 8

Third-order cumulant maps for a point support data used, b fully known block support image V, c training image, and d the average map of the 15 simulated realizations

Full size image
Fig. 9
figure 9

Slices of the fourth-order cumulant maps for a fully known image V, b training image, and c average map of the 15 simulations, all at block support scale

Full size image

The fourth-order cumulant map reproduces the characteristics that are closer to the TI than the fully known image, as expected. Note that, by explicitly calculating the spatial high-order cumulants, the information received from the training image to infer local cross-support distributions is conditioned to the data.

4 Application at a Gold Deposit

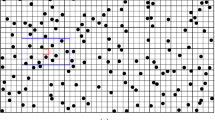
This section applies the proposed method at a gold deposit. The dataset comprises 2300 drillholes spaced approximately in a 35 × 35 m2 configuration, covering an area of 4.5 km2. The training image is defined on 405 × 445 × 43 grid blocks of size 5 × 5 × 10 m3 and is based on blasthole samples. Both inputs are composited in a 10 m bench and are considered to be at point support scale. Figure 10 presents the drillholes available and the training image at block scale. The deposit to be simulated is represented by 510,800 blocks, each measuring 10 × 10 × 10 m3.

Fig. 10
figure 10

a Cross-section of the available drillhole locations, and b training image at block support scale

Full size image

Fifteen simulated realizations are generated; cross-sections from two of them are presented in Fig. 11 to show similarities with the data and TI in the corresponding cross-section in Fig. 10. Notable is the reproduction of a sharp transition from high to low grades. Figure 12 shows the histograms of the simulations and TI at block support scale. Table 3 presents the related statistics. Variograms at block support scale are displayed in Fig. 13, where the data variogram is regularized to reflect the corresponding volume–variance relation. The second-order spatial statistics of the simulations match reasonably with the pattern followed by the data and are close to those of the TI. Results for third- and fourth-order cumulants and related maps for the data, TI, and simulated realizations are shown in Figs. 14 and 15, respectively. Note that the high-order statistics of the simulated realizations match those of the data and TI.

Fig. 11
figure 11

Cross-section of two simulated realizations

Full size image
Fig. 12
figure 12

Histograms of simulated realizations and training image

Full size image
Table 3 Basic statistics of the average of the simulations and training image at block support scale and dataset at point scale
Full size table
Fig. 13
figure 13

Variograms of simulated realizations and training image and data variograms rescaled to represent block variance: WE direction (left) and NS direction (right)

Full size image
Fig. 14
figure 14

Third-order cumulant maps, obtained with the template on the left, for the a dataset, b training image at block support, and c average map of the 15 simulations

Full size image
Fig. 15
figure 15

Three slices of the fourth-order cumulant maps, obtained with the template at the bottom, for the a dataset, b training image at block support, and c average map of the 15 simulations

Full size image

Further highlighting the advantages of the proposed direct block high-order simulation method, note that, for this case study, the runtime of the related algorithm was approximately 5.5 h, while the point high-order simulation requires approximately 24 h. Both approaches are tested with the same specifications and computing equipment: Intel® Core™ i7-7700 CPU with 3.60 GHz, 16 GB of RAM, running under Windows 7.

5 Conclusions

This paper presents a new high-order simulation method that simulates directly at block support scale by estimating, at every block location, the cross-support joint probability density function. Legendre-like splines are the set of basis functions used to approximate the above density function. The related coefficients are calculated from replicates of a spatial template employed. The latter template is generated from the configuration of the block to be simulated and associated conditioning values, whose support can be at both point and block scale. The high-order character of the proposed direct block simulation method ensures that the generated realizations reflect the complex, nonlinear spatial characteristics of the variables being simulated and reproduce the connectivity of extreme values.

The proposed algorithm is tested using an exhaustive image, showing that the different realizations generated can reasonably reproduce spatial architectures observed in the exhaustive image. An application at a gold deposit shows the practical aspects of the method. In addition, it documents that the method works well, while simulated realizations are shown to reproduce the spatial statistics of the available data up to the cumulants of fourth order that were calculated. Further work will focus on improving the computational efficiency, generating training images that are consistent with the high-order relations in the available data, and extending the proposed method to jointly simulate multiple variables.