1 Introduction

In recent years, there has been a major upsurge of research activity in the statistics of extreme events for spatial settings. One reason for this is the realisation among stakeholders (such as climate scientists, environmental engineers, and insurance companies) that in an evolving climate it may be changes in the sizes and frequencies of rare events, rather than changes in the averages, that lead to the most devastating losses of life, damage to infrastructure, and so forth. While it is difficult or even impossible to attribute particular events to the effect of climatic change, the types of events that have long been forecast to increase in frequency by the modeling community—such as heatwaves leading to crop failure and major brush fires, or heavy summer rainfall leading to widespread flooding—do indeed seem to be appearing more often than in the recorded past. This motivates attempts to model such events, in order to understand their likely future impacts, and to assess the related risks.

Classical geostatistics is a well-developed field surveyed in numerous textbooks (Cressie 1993; Wackernagel 2003; Banerjee et al. 2004; Diggle and Ribeiro 2007; Cressie and Wikle 2011), with much software available and a wide range of user communities corresponding to its many applications. Its basis in Gaussian distributions makes it unsuitable for extremal modeling, however, because the Gaussian density function has an exceptionally light tail and, therefore, can badly underestimate probabilities associated to extreme events. Moreover, the tails of the multivariate Gaussian distribution lead to independent extremes, for any underlying correlation that is less than unity, resulting in potentially disastrous underestimation of the probabilities of the simultaneous occurrence of two rare events. This is the formula that killed Wall Street which, at least according to Wired magazine (Salmon 2009), has played a key role in the ongoing international financial crisis by providing wildly incorrect assessment of economic risks.

2 Basic Ideas

2.1 Univariate Extremes

Since Gaussian densities do not provide suitable models for extremes, it is natural to ask what distributions can arise as limits for maxima of independent random variables. An argument originally due to Fisher and Tippett (1928) and subsequently greatly extended (Leadbetter et al. 1983; Galambos 1987; Resnick 2006; de Haan and Ferreira 2006) shows that the suitably rescaled maxima of independent random variables, and of a wide variety of random processes, follow the generalized extreme-value distribution (GEV)

$$ H(y) = \begin{cases} \exp [- \{1 + \xi{(y-\mu)/\tau} \}_+^{-1/\xi} ],&\xi \neq0,\\\exp [-\exp \{-(y-\mu)/\tau \} ],&\xi=0, \end{cases} $$
(1)

where a +=max(a,0), \(\mu\in \mathbb {R}\), τ>0 and \(\xi\in \mathbb {R}\). The quantities μ and τ in Eq. (1) are respectively location and scale parameters, and the shape parameter ξ determines the weight of the upper tail of the density, with increasing ξ corresponding to higher probabilities of large events. Environmental data rarely display |ξ|>1, and often estimates of ξ lie in the interval (−1/2,1/2), but data from finance and telecommunications applications may have heavier tails, with ξ>1. The value of ξ has implications for inference, since the rth moment of Eq. (1) exists only if ξ<1/r, and the regularity conditions for standard likelihood inference hold only for ξ>−1/2. Thus, moment- or likelihood-based inference may perform poorly, and alternative approaches, such as probability-weighted moments (Hosking et al. 1985; Hosking and Wallis 1987) or penalised likelihood (Martins and Stedinger 2000), have been promoted for use in simple settings. However, in more complex applications such as those described below, their flexibility and generality have made likelihood and Bayesian approaches essential.

Equation (1) provides the natural class of models for maxima, from which corresponding models for other definitions of extremes, such as exceedances over high thresholds, may be derived. To be more precise, if extremes of a stream of independently identically distributed random variates are defined in terms of exceedances over a threshold u, then under the rescaling that yields Eq. (1) as the distribution of a maximum and a suitable time rescaling, exceedances of u arise as a Poisson process on the set [0,1]×[u,∞) with measure

$$ \varLambda\bigl\{[t_1,t_2]\times[x,\infty) \bigr\} = (t_2-t_1) \times \bigl\{1 + \xi {(x-\mu)/\tau} \bigr\}_+^{-1/\xi},\quad x>u, \xi\neq0, $$
(2)

and with the same parameters as in Eq. (1); when ξ=0 the second factor on the right of Eq. (2) is replaced by exp{−(x−μ)/τ}. This implies that the times of exceedances of u occur according to a Poisson process of constant rate \(\lambda= \{ 1 + \xi{(u-\mu)/\tau} \}_{+}^{-1/\xi}\), and that conditional on there being an exceedance X>u at time t, we have

$$ \operatorname{Pr}(X>x+u\mid X>u) = \begin{cases} (1 + \xi x/\sigma )_+^{-1/\xi},&\xi\neq0,\\\exp(-x/\sigma), &\xi=0, \end{cases} \quad x>0, $$
(3)

where σ=τ+ξu is a scale parameter, and ξ takes the same value as in Eq. (1), so that ξ=0 corresponds to an exponential distribution of exceedances. Equation (3) is the survivor function of the generalized Pareto distribution (GPD). This provides a semiparametric approximation to the distribution function underlying a random sample, whereby the empirical distribution function of the data is used below the threshold u, and the generalized Pareto distribution is fitted to those observations that exceed u. This involves the estimation of three parameters: the probability of exceeding u, and the GPD parameters σ and ξ.

Equation (1) satisfies the max-stability property: for any \(m\in \mathbb {N}\) there exist real numbers a m >0 and b m such that

$$ H^m(b_m+a_mx) =H(x),\quad x\in \mathbb {R}. $$
(4)

This necessary condition for a limiting distribution for maxima is satisfied only by the GEV, giving it strong mathematical support as a suitable distribution for fitting to maxima of scalar random variables. A corresponding notion of threshold stability gives cogent arguments for fitting of the GPD to exceedances over high thresholds. Lower extrema are treated simply by noting that min(X 1,…,X n )=−max(−X 1,…,−X n ). The results for maxima or for exceedances over a threshold are simply applied to a transformed version of the original variables, followed by a back-transformation. If the observations are identically distributed but not independent, then under fairly mild conditions the renormalized maxima continue to follow Eq. (1) with the same value of ξ, but threshold exceedances occur as a compound Poisson process, with clusters of mean size θ −1, where θ∈(0,1] is known as the extremal index. The limiting distribution of cluster maxima remains Eq. (3), and this is the same distribution as that of an arbitrary exceedance. For more details, see Leadbetter et al. (1983), Hsing (1987), Hsing et al. (1988), and Leadbetter (1991).

2.2 Outline

Statistical models derived from Eqs. (1), (2), and (3) have been widely used in applications for decades (Gumbel 1958; Smith 1989; Davison and Smith 1990; Coles 2001; Beirlant et al. 2004), but modeling in the spatial and space-time domains is much more recent. It rests on extensions of Eq. (1) that satisfy an appropriate generalization of Eq. (4). In Sect. 3, we outline the construction of max-stable processes, and then sketch how inference for them is conducted. Other reviews, also involving comparisons with other approaches, include Davison et al. (2012) and Cooley et al. (2012a).

Max-stable processes Z(x) defined on a spatial domain \({\mathcal{X}}\) are asymptotically dependent: the conditional probability distribution of their values at two spatial locations, or sites, x 1 and x 2, that differ by a lag vector h, satisfies

$$ \chi_h=\lim_{z \rightarrow\infty} \Pr\bigl \{Z(x_1)>z \mid Z(x_2)>z\bigr\} , \quad x_1,x_2 \in {\mathcal{X}}, $$
(5)

where a strictly positive limit implies that a large event at x 2 leads to a non-zero probability of a similarly large event at x 1. However, in some applications, it seems that χ h =0, and then so-called asymptotic independence models may be preferred; Gaussian process models are asymptotically independent. In this case, the rate at which the limit in Eq. (5) is approached is of critical importance. Apart from the Gaussian model, one class of such models consists of the so-called inverted max-stable models discussed in Sect. 4.1. In Sect. 4.2, we describe measures of dependence that are suitable either for asymptotic dependence or independence models, or to help to discriminate between them, and in Sect. 5 we discuss two applications of these different models for extremes in geosciences.

3 Max-Stable Processes

3.1 Basic Ideas

Consider annual maxima of some phenomenon, such as temperature or daily rainfall, observed at a set of sites \({\mathcal{D}}=\{x_{1},\ldots, x_{D}\}\) within a spatial domain \({\mathcal{X}}\). It is natural to treat the corresponding observations Z(x 1),…,Z(x D ) as stemming from a process Z(x) defined for all \(x\in {\mathcal{X}}\) (with the natural model for each of these individually given by Eq. (1)) but with location, scale and shape parameters taken to be spatially-varying surfaces, giving μ(x), τ(x) and ξ(x), for \(x\in {\mathcal{X}}\). These surfaces may also depend on explanatory variables, such as distance from a coast or altitude. In applications, they may be taken to be polynomials or use basis functions such as thin-plate splines, and their parameters may be estimated using likelihood methods. A closely related approach, typically used in Bayesian modeling using Markov chain Monte Carlo simulation, is to represent variation in extremal parameters through spatial Gaussian processes. For example, Cooley et al. (2007) fit rainfall exceedances using a GPD model (Eq. (3)) in which logσ follows such a process, but the shape parameter has two values, and many similar models have appeared in the literature (Coles and Casson 1998; Casson and Coles 1999; Sang and Gelfand 2009, 2010). Chavez-Demoulin et al. (2011) point out that inclusion of covariates in the usual parameterization of the GPD model leads to a lack of invariance to the choice of threshold that can be resolved using the GEV parameterization. One major difference between models such as that of Cooley et al. (2007) and those proposed below is that the former fit univariate extremal distributions to data at particular spatial locations, but treat the margins as independent, conditional on the covariates, so risk estimates for spatial quantities may be poor, though those at individual locations can be expected to improve because of borrowing of strength across the spatial domain. By contrast, the models described here aim to capture joint spatial properties of extremes in addition to their marginal variation.

The exposition below is simplified if we assume that these marginal surfaces are known, in which case we can transform the original data so that Z(x) has a unit Fréchet distribution, that is, \(\operatorname{Pr}\{Z(x)\leq z\} = \exp(-1/z)\), for z>0 and each \(x\in {\mathcal{X}}\). The notion of max-stability extending Eq. (4) is that for each m=1,2,… , there exist continuous functions a m (x)>0 and b m (x) such that for suitable functions z(x)

$$ \operatorname{Pr}\bigl\{Z(x)\leq b_m(x) + a_m(x)z(x) , x\in {\mathcal{X}}\bigr\}^m = \operatorname{Pr}\bigl\{Z(x)\leq z(x), x\in {\mathcal{X}}\bigr\}, $$
(6)

or, equivalently, Z(x) and the maximum of m independent copies of {Z(x)−b m (x)}/a m (x) have the same distribution. A continuity argument implies that this is true for any m>0. The natural extension of the GEV is the class of max-stable processes, which, under mild conditions, comprise the only possible non-degenerate limits of linearly rescaled component-wise maxima of identically distributed processes (de Haan and Ferreira 2006). They thus provide natural models for processes of maxima. Max-stable processes may be represented in the form (de Haan 1984; Schlather 2002)

$$ Z(x) = \max_{i=1,\ldots, \infty} W_i(x)/T_i, \quad x\in {\mathcal{X}}, $$
(7)

where 0<T 1<T 2<⋯ are the points of a unit rate Poisson process on \(\mathbb {R}_{+}\) and the W i (x) are independent replicates of a positive continuous stochastic process W(x) on \({\mathcal{X}}\) that satisfies E{W(x)}≡1 and certain technical conditions. The representation of Eq. (7) may be interpreted in terms of a storm process, where the W i (x) are storm shapes and the \(T_{i}^{-1}\) their intensities, and the largest storm observed at each site x is recorded. Following Schlather (2002), it is possible to check that Eq. (7) satisfies Eq. (6) and has unit Fréchet marginal distributions, and that

$$ \operatorname{Pr}\bigl\{ Z(x)\leq z(x), x\in {\mathcal{X}}\bigr\} = \exp \biggl( -\mathrm{E}\biggl[ \sup_{x\in {\mathcal{X}}} \biggl\{ {W(x)\over z(x)} \biggr\} \biggr] \biggr). $$
(8)

By setting z(x d )=z d for d=1,…,D and z(x)=+∞ elsewhere, we see that the joint cumulative distribution function of Z(x 1),…,Z(x D ) equals exp{−V(z 1,…,z D )}, where the function

$$ V(z_1,\ldots, z_D) = \mathrm{E}\biggl[\max _{d\in\{1,\ldots, D\}} \biggl\{ {W(x_d)\over z_d} \biggr\} \biggr], $$
(9)

is known as the exponent measure. This is easily shown to be homogeneous of order −1, and must satisfy V(∞,…,z d ,…,∞)=1/z d in order that each of the marginal distributions is unit Fréchet. To sketch one important implication of the homogeneity, let us write z=z(x) and define the pseudo-polar coordinates r=∥z∥ and w=z/∥z∥, where ∥⋅∥ represents a norm. Then it can be shown that the exponent measure factorizes as a product of two measures, one depending on the pseudo-radius r and the other on the pseudo-angle w. This factorization underpins extrapolation to high levels, since it implies that the angular component can be estimated from observed data, and then used to extrapolate beyond the observations, through the regularity of the radial component. See de Haan and Resnick (1977) and Beirlant et al. (2004, Sect. 8.2.3). Equation (9) may be used to compute V(z 1,…,z D ) for certain choices of W(x), but typically it is only explicitly available for D=2 (Genton et al. 2011; Huser and Davison 2013; Wadsworth and Tawn 2013), so that full likelihood inference based on Eq. (8) seems unattainable in general; see Sect. 3.3.

For any pairs of sites \(x_{1},x_{2}\in {\mathcal{X}}\), the strength of dependence between Z(x 1) and Z(x 2) may be summarized by the extremal coefficient θ(h)=V(1,1)∈[1,2], where h=x 1−x 2 is the lag vector, with θ(h)=1 corresponding to perfect dependence and θ(h)=2 to independence. There is an equivalence with the limiting probability χ h in Eq. (5), since χ h =2−θ(h), so χ h =1 for perfectly dependent models, and χ h =0 for independent and asymptotically independent cases. Thus, one expects θ(h) to be monotonic increasing in ∥h∥, analogous to the variogram of a spatial process. Analogues to θ(h) may be defined for more than two sites (Schlather and Tawn 2003), and are useful for model-checking.

3.2 Models

Equation (7) and suitable choices of W(x) can be used to construct max-stable models. The Gaussian extreme value process (Smith 1990), often referred to as the Smith model, a realization of which is shown in the left panel of Fig. 1, is constructed by taking W(x) to be a bivariate Gaussian density centered at a random point that is uniformly distributed in the spatial domain. This model seems too smooth to be useful in applications, and in this respect it is unfortunate that it was the first model to be fitted (Padoan et al. 2010), and thus has in some sense become a standard. Non-smooth processes are more suited for modeling natural phenomena. The Schlather (2002) model, a realization of which is shown in the right panel of Fig. 1, takes

$$ W(x)=\sqrt{2\pi}\max\bigl\{0,\varepsilon (x)\bigr\}, $$
(10)

where ε(x) is a stationary centred Gaussian process with unit variance and correlation function ρ(h). The smoothness of the resulting process can be controlled by the choice of correlation function. However, the Schlather model is not ergodic in the sense that it cannot attain independence of Z(x 1) and Z(x 2) unless corr{ε(x 1),ε(x 2)}=−1; equivalently its extremal coefficient θ(h) is bounded below 2 for any h (Kabluchko and Schlather 2010; Davison and Gholamrezaee 2012). To circumvent this, Schlather (2002) proposed to introduce a random set element that ensures that sites that are distant enough cannot be covered by the same random function W i (x) in Eq. (7), and thus yields exact independence between maxima at such sites. Another possibility, which can be viewed as extending the Smith model (Huser and Davison 2013), is the Brown–Resnick process (Brown and Resnick 1977; Kabluchko et al. 2009), sometimes called the geometric Gaussian process. This is constructed by using Eq. (7) with

$$ W(x) = \exp\bigl\{\varepsilon (x)- \gamma(x)\bigr\}, $$
(11)

where ε(x) is an intrinsically stationary Gaussian process with mean zero, semivariogram γ(h), and ε(0)=0 almost surely. Brown–Resnick processes can be shown to be essentially the only limit of properly rescaled maxima of Gaussian processes (Kabluchko et al. 2009) and have been found to yield good fits in applications (Davison et al. 2012; Jeon and Smith 2012). Their flexibility, and the recent development of efficient inference procedures (Engelke et al. 2012; Wadsworth and Tawn 2013), make them particularly attractive. Although Brown–Resnick processes are based on nonstationary Gaussian models, the construction in Eq. (7) ensures that their distributions are stationary and highly non-Gaussian. Furthermore, methods for simulating Brown–Resnick processes have been developed (Oesting et al. 2012; Schlather 2002; Ribatet 2011), though they are more computationally intensive than for the Schlather or Smith models. As for the univariate case with the GPD and the Poisson process of exceedances sketched in Sect. 2.1, the results for maxima can be generalized naturally to the modeling of threshold exceedances. Loosely speaking, it can be shown that under similar conditions, the dependence structure of very high spatial events, not necessarily maxima, converges to that of a max-stable process, so the models described above can also be applied for excesses of very large thresholds.

Fig. 1
figure 1

Max-stable processes, with unit Fréchet margins, simulated from (a) the Smith model, for which W(x) is a Gaussian density with covariance matrix whose diagonal and off-diagonal elements equal 0.1 and 0.05, respectively; (b) the Schlather model, ε(x) having stable correlation function ρ(h)=exp(−2∥h∥)

Full size image

3.3 Inference

Owing to the complicated form of the density stemming from differentiation of Eq. (8) with Eq. (9), classical likelihood inference for the parameters of max-stable models is not possible in general, and recourse has been made to composite likelihoods (Varin et al. 2011) based on lower-order marginal densities, such as bivariate margins of all pairs of maxima. Under mild conditions, maximum composite likelihood estimators are strongly consistent and have asymptotic normal distributions, though they may be much more variable than ordinary maximum likelihood estimators (Huser and Davison 2013; Davis and Yau 2011). The composite likelihood information criterion, CLIC, the analogue of the AIC for composite likelihoods, allows model comparison (Varin and Vidoni 2005; Davison and Gholamrezaee 2012). More recently, inference methods based on the full likelihood have been proposed for a special class of max-stable processes that includes the Brown–Resnick processes (Wadsworth and Tawn 2013), and Engelke et al. (2012) proposed to fit Brown–Resnick processes based on the full likelihood of extremal increments of the process. From the Bayesian perspective, Ribatet et al. (2012) have developed a Monte Carlo Markov chain algorithm for fitting such models by sampling the composite posterior distribution using a modified acceptance rate. Reich and Shaby (2012) and Shaby and Reich (2012) describe the fitting of a Bayesian hierarchical model built from a finite approximation to a max-stable process, based on latent α-stable variates.

When individual events are recorded, more efficient inference is feasible. Since the max-stable models are suitable only above some predetermined high threshold, inference is usually made using a censored approach (Huser and Davison 2013, 2013; Jeon and Smith 2012; Thibaud et al. 2013). Furthermore, following Stephenson and Tawn (2005), Davison and Gholamrezaee (2012) and Wadsworth and Tawn (2013) show how to incorporate the occurrence times of extreme events, use of which both simplifies the likelihood and allows much more efficient inference in cases of moderate to low spatial dependence.

4 Asymptotic Dependence and Independence

4.1 Models for Asymptotic Independence

As mentioned in Sect. 1, stationary max-stable processes Z(x) with unit Fréchet marginal distributions are asymptotically dependent in the sense that

$$ \chi_h=\lim_{z \rightarrow\infty} \Pr\bigl \{Z(x_1)>z \mid Z(x_2)>z\bigr\} = 2 - \theta(h), \quad x_1,x_2 \in {\mathcal{X}}, $$
(12)

where h=x 1−x 2 is the lag vector, and χ h may be strictly positive. In practice it may be difficult to identify independence of extremes based on finite samples, since the data may display residual dependence for any finite threshold, however high. Asymptotic independence models, for which the limit in Eq. (12) equals zero, but which can also model the dependence present before the limit is reached, may therefore be preferred for modeling at finite thresholds. The Gaussian model is asymptotically independent for all correlations ρ(h)≠1, but Gaussian processes are too restrictive in the bulk of extremal applications, so broader classes of models are needed to allow flexible modeling. Let Z(x) denote a stationary process for spatial extremes with unit Fréchet margins. In order to smoothly link asymptotic dependence and independence in two dimensions, Ledford and Tawn (1996) proposed a model in which

$$ \Pr\bigl\{Z(x_1)>z \mid Z(x_2)>z\bigr\} \sim\mathcal{L}(z) z^{1-1/\eta(h)}, \quad z\to\infty, $$
(13)

where the function \(\mathcal{L}(z)\) is slowly varying at infinity, that is, \(\lim_{t\to\infty} \mathcal{L}(ta)/\mathcal{L}(t)=1\), for any a>0, and η(h)∈(0,1] is called the coefficient of tail dependence. If η(h)=1, then the limit in Eq. (13) depends on \(\mathcal{L}(z)\) and is typically non-zero, cf. Eq. (12), whereas if η(h)<1, then asymptotic independence arises: the dependence decreases with the size z of the rare event, at a rate determined by η(h). In the case of a Gaussian process, η(h)={1+ρ(h)}/2. The variables are positively associated when η(h)>1/2 and negatively associated when η(h)<1/2. So-called near-independence corresponds to η(h)=1/2, since in that case the conditional survivor function Eq. (13) corresponds to that of a Fréchet distribution. Further bivariate asymptotic independence models have been proposed, notably by Ledford and Tawn (1997) and Ramos and Ledford (2009, 2011). It turns out that the lower tail of a multivariate max-stable distribution is asymptotically independent, and this motivated Wadsworth and Tawn (2012) to introduce the class of inverted max-stable processes, which are defined in terms of a max-stable process Z(x) by

$$ Z'(x) = - 1/\log\bigl[1-\exp\bigl\{-1/Z(x)\bigr\}\bigr], \quad x\in \mathcal{X}, $$
(14)

and which provide spatial models for asymptotic independence. For these processes, η(h)=1/θ(h), where θ(h) is the extremal coefficient of Z(x). With this construction, each max-stable model Z(x) may be transformed to provide an asymptotically independent counterpart Z′(x). Figure 2 depicts conditional exceedance probabilities for max-stable, Gaussian and inverted max-stable processes, for various levels of dependence. The difference between these asymptotic dependence and asymptotic independence models is striking; for the former, the conditional probabilities are convex in z and converge to a positive value, whereas for the latter they are concave in z and tend to zero. The probabilities for the Gaussian and inverted max-stable processes tend very slowly to zero, and although both models are asympotically independent they can be quite different at finite thresholds due to differences in the slowly varying functions in Eq. (13).

Fig. 2
figure 2

Theoretical conditional exceedance probabilities p(z)=Pr{Z(x 1)>z∣Z(x 2)>z} for (a) a max-stable process with θ(h)=1, 1.2, 1.4, 1.6, 1.8, 2 (from top to bottom); (b) a Gaussian process with correlation ρ(h)=0, 0.25, 0.75, 0.9, 0.95, 1 (from bottom to top); (c) an inverted max-stable process with η(h)={1+ρ(h)}/2, and the same values of ρ(h) as in (b) (also from bottom to top). The margins are uniform on [0,1]

Full size image

Wadsworth and Tawn (2012) proposed the use of hybrid models, that is, mixtures of max-stable and inverted max-stable processes that can assure asymptotic dependence at short distances and asymptotic independence at larger ones. As with max-stable processes, such models can be fitted using composite likelihood, and can be compared using the CLIC.

4.2 Measures of Extremal Dependence

Different measures of extremal dependence have been proposed. The extremal coefficient θ(h), introduced in Sect. 3, is suitable for asymptotically dependent processes, whose renormalized maxima converge to a nontrivial max-stable process. Empirical estimators of θ(h), based on the assumption of max-stability, have been suggested by Schlather and Tawn (2003) and Naveau et al. (2009), the latter based on the madogram, an analogue of the variogram for extremal processes. These estimators appear to yield satisfactory results within the max-stable framework, but cannot distinguish different degrees of asymptotic independence. The coefficient of tail dependence η(h), introduced in Sect. 4.1, is suited for asymptotically independent variables, and can be estimated by maximum likelihood (Ledford and Tawn 1996) using min{Z(x),Z(x+h)}. However, since the case η(h)=1 corresponds to the entire class of max-stable processes, it provides no information about the strength of dependence of a given max-stable process. Moreover, discriminating between asymptotic dependence and asymptotic independence is difficult, because the dependence between variables may vanish very slowly as the level increases; see Fig. 2. Ledford and Tawn (1996) discuss testing for asymptotic independence. Coles et al. (1999) suggested model-free diagnostics χ h (u) and \(\bar{\chi}_{h}(u)\) for distinguishing among these different types of tail dependence. If Z(x 1) and Z(x 2) are assumed to have uniform marginal distributions, then these coefficients can be expressed as

$$ \chi_h(u)=2-{\log C(u,u)\over\log u}, \qquad\bar{\chi}_h(u)={2 \log (1-u)\over\log\bar{C}(u,u)}-1, \quad0\leq u\leq1, $$
(15)

where C is the joint cumulative distribution function of Z(x 1) and Z(x 2), also called their copula (Nelsen 2006), and

$$\bar{C}(u_1, u_2) = \operatorname{Pr}\bigl\{Z(x_1)>u_1, Z(x_2)>u_2\bigr\} $$

is the corresponding bivariate survivor function. The dependence measures in Eq. (15) are often estimated by their empirical rank-based counterparts, though the model-based estimators mentioned above will be more efficient, at least when the underlying model is reasonable. Note that lim u→1 χ h (u)=χ h , as defined in Eq. (5). The coefficient χ h (u), whose sign indicates whether the variables are positively or negatively associated for a given u (Nelsen 2006), is equivalent to the conditional probability Pr{Z(x 1)>u∣Z(x 2)>u} when u→1. In case of asymptotic independence, lim u→1 χ h (u)=0, and χ h (u)≡0 for exactly independent variables. If the variables are max-stable with extremal coefficient θ(h), then χ h (u)≡2−θ(h)≥0.

The coefficient \(\bar{\chi}_{h}(u)\) provides a measure of dependence within the class of asymptotically independent processes. One can show that under Eq. (13), \(\bar{\chi}_{h}(u)\to2\eta(h)-1\), as u→1. Furthermore, for any inverted max-stable process, \(\bar{\chi}_{h}(u)\equiv 2\eta(h)-1\). Figure 3 displays χ h (u) and \(\bar{\chi}_{h}(u)\) for max-stable, Gaussian and inverted max-stable processes. For max-stable processes, χ h (u) is constant and \(\bar{\chi}_{h}(u)\) increases to unity; for Gaussian processes, χ h (u) decreases to zero and \(\bar{\chi}_{h}(u)\) increases to 2η(h)−1; and for inverted max-stable processes, χ h (u) decreases to zero and \(\bar{\chi}_{h}(u)\) takes the constant value 2η(h)−1. Hence, in this sense, the Gaussian model has even lighter tails than the left tail of a max-stable process.

Fig. 3
figure 3

The dependence measures χ h (u) and \(\bar{\chi}_{h}(u)\) for a max-stable process with θ(h)=1.7 (red), a Gaussian process with ρ(h)=0.7 (blue) and an inverted max-stable process with η(h)={1+ρ(h)}/2=0.85 (green)

Full size image

Similar dependence measures for extremes of time series are described by Ledford and Tawn (2003) and Davis and Mikosch (2010).

5 Applications

The ideas outlined above have been applied to a variety of extremal problems, often with further explanatory variables used to account for variation in the surfaces μ(x), τ(x), and ξ(x), though ξ(x) is often found to be constant. Buishand et al. (2008) take a semiparametric approach to max-stable modeling for rainfall data in a homogeneous region of the Netherlands. Padoan et al. (2010) fit the Smith model to annual maximum daily rainfall at 46 sites in the Appalachian mountains, and find that their best max-stable model fits reasonably well. Blanchet and Davison (2011) use similar models, but with regional effects and a third dimension, namely altitude, in a study of maximum snow depth in the Swiss Alps. Davison et al. (2012) compare a variety of models for extreme rainfall, including some based on copulas, Bayesian hierarchical distributions and max-stable models, and conclude that the latter fit best, but that the Smith model is clearly beaten by rougher processes like those in the right-hand panel of Fig. 1. Davison and Gholamrezaee (2012) apply the Schlather model with a random set to data on extreme temperatures, a relatively large-scale phenomenon compared to rainfall, and Huser and Davison (2013) have extended this to space-time modeling of extreme rainfall. Shang et al. (2011) and Westra and Sisson (2011) use the Smith model to study dependence in extreme rainfall on regional scales, including the influence of climate variables such as the Southern Oscillation Index. Reich and Shaby (2012) and Shaby and Reich (2012) fit the Bayesian latent variable approximation to a max-stable process mentioned above to rainfall and extreme temperature data. Max-stable processes appear to be well suited for modeling rainfall and temperature processes at various scales. The use of inverted max-stable models is more recent. Wadsworth and Tawn (2012) show that max-stable processes are not well adapted for modeling wave height data in North Sea and that inverted models are preferred. Thibaud et al. (2013) compare the fits of Gaussian, max-stable, and inverted max-stable models for extreme spatial rainfall in a small mountain catchment, and conclude that the last fits their data best.

Below we discuss a small spatial application using data on air temperature and precipitation, and find that asymptotic dependence models may be preferred for the first dataset, but that asymptotic independence models seem to fit better for the second. Gaussian models perform less well in both cases. We consider winter daily temperature minima and summer daily cumulative rainfall, recorded at eight monitoring sites with similar altitudes and located in the so-called plateau region of Switzerland; see Fig. 4. The data were available from 1981 to 2012, giving a total of about 2,900 observations per site. For simplicity, we treat these daily data as independent over time, although this is false at least for the temperature data. A more complex spatiotemporal study was performed by Huser and Davison (2013), where further details about part of the rainfall data may be found. They fit several space-time max-stable models to hourly rainfall, of which the Schlather model with random set seemed to be well-suited, but did not compare them to asymptotic independence models.

Fig. 4
figure 4

Topographic map of monitoring sites (with their altitudes) from MeteoSwiss, where temperature and precipitation data were recorded. The most distant sites are 107 km apart, while the closest are 16 km apart

Full size image

We first transformed the temperature data by multiplication by −1, and then fitted the generalized Pareto distribution (Eq. (3)) to model events above the 98 % quantile, u 98, of the time series at each site separately, and used this fitted model to transform the data to have the unit Fréchet distribution. Since Bortot et al. (2000) and Coles and Pauli (2002) have shown that the choice between asymptotic dependence and asymptotic independence models can influence extrapolation and association of extremes far more than the particular model used in each of these model classes, we fit only a limited selection of spatial correlations for this illustrative analysis. For each dataset, we used a censored pairwise threshold-based approach (Huser and Davison 2013) to fit three models to the exceedances over u 98: (a) the max-stable Brown–Resnick model in Eq. (11), with variogram 2γ(h)=σ 2 I(h>0)+(∥h∥/λ)α, where σ>0 is a nugget effect, I(⋅) denotes the indicator function, λ>0 is a range parameter and α∈(0,2] is a smoothness parameter; (b) the corresponding inverted max-stable model; and (c) the multivariate Gaussian distribution, transformed to unit Fréchet margins, with correlation function ρ(h)=exp{−2γ(h)}. Larger values of α give smoother processes in each case. For the temperature data, α was always estimated very close to its upper boundary, so we set α=2 and estimated only the remaining parameters. Table 1 reports the estimated parameters and confidence intervals, and the corresponding scaled values of the log pairwise likelihood and CLIC, for each model and dataset. There is a strong difference in the scales and in the smoothness of the processes. The temperature data have \(\hat{\lambda}=210\) km or more, and α=2, corresponding to a relatively smooth process with large-scale dependence, though local variation is accommodated by the nugget σ 2, which is significantly larger than zero. The rainfall data have \(\hat{\lambda}>3\) km and \(0<\hat{\alpha}<1\), corresponding to a much rougher process, with a nugget whose confidence interval almost includes zero. There is a clear trade-off between including a nugget to allow local variation in a max-stable process, and of using an asymptotically independent process, in which local variation can be stronger; the availability of data at nearby locations might allow better discrimination between these. In each case the value of \(\hat{\lambda}\) is smallest for the max-stable process and seems unrealistically large for the Gaussian process. The rather wide confidence intervals for λ for the temperature data probably stem from the difficulty of estimating continental-scale events from data over a limited region of a small country.

Table 1 Estimated dependence parameters \(\hat{\sigma}^{2}\), \(\hat{\lambda}\) and \(\hat{\alpha}\) (with 95 % confidence intervals based on block bootstrap using seasonal blocks) from the models (a), (b), and (c), along with the value of the log pairwise likelihood, \(\hat{\ell}\), evaluated at the parameter estimates and scaled in such a way that its value is comparable to the log likelihood under independence, as suggested by Davison and Gholamrezaee (2012). The values of the CLIC⋆, a scaled version of the CLIC, are also reported
Full size table

Figure 5 displays binned empirical estimates of the extremal coefficient θ(h) for the temperature data, for which the best model is max-stable, and of the coefficient of tail dependence η(h) for the rainfall data, which seem asymptotically independent. Comparing these estimates to their fitted counterparts, it seems that the models capture spatial dependence quite flexibly. The graphs confirm that the natural processes considered here have decreasing extremal dependence with increasing distance, although dependence remains strong at long distances for temperatures, perhaps explaining the difficulty in estimating the range parameter. The huge uncertainty in these plots would be reduced by taking more sites. Moreover, since the monitoring sites are at least 16 km apart, small local variation represented by the nugget is difficult to estimate.

Fig. 5
figure 5

Extremal coefficient θ(h) (left) and coefficient of tail dependence η(h) (right), corresponding to the best fitted models for the temperatures and rainfall data, respectively. According to Table 1, these models are respectively max-stable and inverted max-stable. Circles are binned empirical estimates with 95 % confidence intervals in grey, while black solid lines are model-based estimates. The black points represent theoretical values of θ(0) and η(0)

Full size image

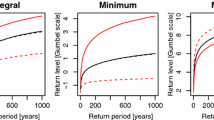
While the best model for the temperature data, according to the CLIC and the value of the log pairwise likelihood, is max-stable, the rainfall data appear to be asymptotically independent. Since max-stable models provide the only possible limiting dependence structure, the fit of these models should be better for higher thresholds, but as finite thresholds must be considered in practice, asymptotic independence models might provide better fits to the available data. If interest resides in extremely high joint return levels, it could be misleading to base inferences on asymptotic independence models. To assess this, Fig. 6 shows the empirical values for χ h (u) and \(\bar{\chi}_{h}(u)\) for the sites NEU (Neuchâtel) and PAY (Payerne), and their model-based counterparts. Although the fits at finite thresholds are similar for the different models, they differ at very extreme thresholds, and the probabilities of very extreme events might be strongly underestimated if an asymptotic independence model is used. The right panels of Fig. 6 display joint return levels for some spatial functionals of the daily temperature and rainfall data recorded at NEU and PAY. At observed timescales, the curves for the different models give more or less the same predictions, but at the 1000 year-return period, a discrepancy of around 7.6 mm appears for the rainfall data, underlining the ability of the max-stable model to capture dependence at high levels. This effect would probably increase for longer return periods and if more sites were to be considered simultaneously. In summary, if there were any guarantees that the data we consider are indeed asymptotically independent, the Gaussian or inverted max-stable models would potentially be suitable, but since it is very difficult, if not impossible, to have insight so far into the tail, it is safer to base risk assessments on max-stable models, which provide upper bounds for joint probabilities of extreme events.

Fig. 6
figure 6

Extremal diagnostics computed for the temperature (top row) and rainfall (bottom row) data for the pair of monitoring sites NEU and PAY. Left–Middle columns: Empirical estimates (circles) of χ h (u) (left) and \(\bar{\chi}_{h}(u)\) (middle) with their model-based counterparts: The solid lines show the fitted curves for (a) the max-stable model (red), (b) the inverted max-stable model (green) and (c) the Gaussian model (blue). The grey vertical lines are 95 % confidence intervals from a block bootstrap using seasonal blocks, and the vertical dashed line is the threshold used when fitting the dependence models. Right column: Empirical and model-based return levels for the spatial average (over both sites) of daily temperature minima (top) and cumulative rainfall (bottom), on the original scale

Full size image

6 Discussion

This paper sketches some of the statistical ideas useful for modeling spatial extremes. Classical geostatistical models based on the Gaussian distribution may provide poor models for maxima or threshold exceedances. Since the multivariate normal distribution belongs to the class of asymptotically independent processes, it may underestimate the probabilities of rare events and thus provide poor risk estimates for spatial functionals. This difficulty also arises for inverted max-stable processes, presented in Sect. 4.1, even though these appear to be more flexible than the Gaussian distribution. Max-stable processes, which assume a degree of dependence that does not change with the severity of the event, are natural models to capture extremal dependence. At finite thresholds these asymptotic dependence models may yield worse fits than flexible asymptotic independence models, but unless the data are truly asymptotically independent, which is difficult to assess in practice, max-stable processes provide a conservative basis for the estimation of probabilities of very rare events. In order to discriminate between asymptotic independence and max-stability, different measures of extremal dependence have been introduced, including the diagnostics χ h (u) and \(\bar{\chi}_{h}(u)\) of Coles et al. (1999). Unlike the extremal coefficient and the coefficient of tail dependence, these two measures are nonparametric. They can be used to check whether the assumption of max-stability is reasonable, but must be interpreted with care at high thresholds. Our data analysis suggests that daily temperature minima, which represent a large-scale phenomenon, tend to favor max-stable models, whereas daily rainfall totals show weaker spatial dependence and seem closer to asymptotic independence. Although spatial return levels at observed time-scales differ little, a discrepancy was visible for the rainfall data at the 1000 year-return period. For space-time data, hybrid models (Wadsworth and Tawn 2012) can capture different asymptotic properties at different distances and time lags, but they may be quite difficult to fit in practice. Coles and Pauli (2002) suggest an approach to merging the uncertainty arising from the dichotomy between the two types of asymptotic behavior, but it is unclear how it might be applied in the spatial context.

An alternative approach is the use of conditional models for extremes, in which the behavior of several variables is considered, conditioned on the event that one of them is extreme. Following its introduction by Heffernan and Tawn (2004), this approach has been developed from the theoretical viewpoint by Heffernan and Resnick (2007), Das and Resnick (2011), and Fougères and Soulier (2012), among others, and has been applied to spatial flood estimation by Keef et al. (2009, 2013). Related work is described by Cooley et al. (2012b). Extrapolation to estimate probabilities of events never yet seen rests entirely on assumptions about the behavior of distribution tails, but these can only be verified with respect to events that have already occurred. Thus, the likely validity of the model underlying the extrapolation needs exceptionally careful consideration. This is compounded in the spatial setting, in which extrapolation from a finite and perhaps unreliable dataset to an infinite-dimensional space is required. This task at first appears impossible, but if used with attention and supplemented with subject-matter knowledge, the ideas sketched in this paper provide initial steps toward a quantitative understanding of spatial rare events.