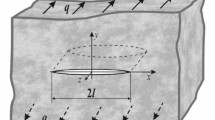
We obtain the solution of a plane problem of the theory of elasticity on the phenomenon of “healing” of a crack in an anisotropic body. By using the model of Winkler’s base, this problem is reduced to a singular integrodifferential equation for the displacements of points of the crack surface. In the case of a defect in the form of flattened ellipse, we obtain the exact analytic solution of the problem. The limit equilibrium state of the plate with a filled crack is estimated by using the energy criterion. We also determine the optimal strength of the injection material after hardening (maximizing the strength of the plate).

Similar content being viewed by others
References
S. G. Lekhnitskii, Anisotropic Plates, Gordon & Breach, New York (1968)
H. A. Elliot, “Three-dimensional stress distributions in hexagonal aeolotropic crystals,” Proc. Cambridge Philos. Soc., 44, Part 4, 522–533 (1948).
G. N. Savin, Distribution of Stresses near Holes [in Russian], Naukova Dumka, Kiev (1968).
G. C. Sih, P. C. Paris, and G. R. Irwin, “On cracks in rectilinearly anisotropic bodies,” Int. J. Fract. Mech., 1, No. 3, 189–203 (1965).
E. M. Wu, “Application of fracture mechanics to anisotropic plates,” J. Appl. Mech. Trans. ASME, 34, No. 4, 967–974 (1967).
L. T. Berezhnitskii, V. V. Panasyuk, and V. M. Sadivskii, “On the influence of the anisotropy of material on the stress intensity factors near cracklike defects,” Probl. Prochn., No. 4, 16–21 (1971).
L. A. Filshtinskii, “Elastic equilibrium of a plane anisotropic medium weakened by arbitrary curvilinear cracks. Limit transition to the isotropic medium,” Izv. Akad. Nauk SSSR, Mekh. Tverd. Tela, No. 5, 91–97 (1976).
N. I. Ioakimidis and P. S. Theocaris, “The problem of the simple smooth crack in an infinite anisotropic elastic medium,” Int. J. Solids Struct., 13, No. 4, 269–278 (1977).
G. I. Barenblatt and G. P. Cherepanov, “On the equilibrium and propagation of cracks in anisotropic media,” Prikl. Mat. Mekh., 25, Issue 1, 45–55 (1961).
S. V. Serensen and G. P. Zaitsev, Bearing Ability of Thin-Walled Structures Made of Reinforced Plastic Materials with Defects [in Russian], Naukova Dumka, Kiev (1982).
V. V. Bozhydarnik and O. V. Maksymovych, Elastic and Limit Equilibrium of Anisotropic Plates with Holes and Cracks [in Ukrainian], Luts'k State Technical University, Luts'k (2003).
V. V. Bozhydarnik, O. E. Andreikiv, and H. T. Sulym, Fracture Mechanics, Strength, and Durability of Continuously Reinforced Composites [in Ukrainian], Vol. 2, Nadstyr’ya, Luts’k (2007).
L. Czarnecki and P. H. Emmons, Naprava i Ochrona Konstrukcji Betonowych, Polski Cement, Krakow (2002).
V. I. Marukha, V. V. Panasyuk, and V. P. Sylovanyuk, Injection Technologies for the Restoration of the Serviceability of Damaged Structures Intended for the Long-Term Operation [in Ukrainian], Spolom, Lviv (2009).
V. V. Panasyuk, V. I. Marukha, and V. P. Sylovanyuk, Injection Technologies for the Repair of Damaged Concrete Structures, Springer, Berlin (2014).
V. P. Sylovanyuk, V. I. Marukha, and N. V. Onyshchak, “Strength of a body containing a crack partially filled with injection material,” Fiz.-Khim. Mekh. Mater., 45, No. 5, 77–80 (2009); English translation: Mater. Sci., 45, No. 5, 696–701 (2009).
V. P. Sylovanyuk, V. I. Marukha, and N. V. Onyshchak, “Residual strength of cylindrical elements with cracks healed by using the injection technology,” Fiz.-Khim. Mekh. Mater., 43, No. 1, 99–104 (2007); English translation: Mater. Sci., 43, No. 1, 109–116 (2007).
V. P. Sylovanyuk and A. V. Revenko, “Long-term strength of an elastic body with elliptic cracks filled with a viscoelastic material,” Fiz.-Khim. Mekh. Mater., 48, No. 1, 33–38 (2012); English translation: Mater. Sci., 48, No. 1, 29–35 (2012).
H. T. Sulym, Foundations of the Mathematical Theory of Thermoelastic Equilibrium of Deformable Solids with Thin Inclusions [in Ukrainian], T. Shevchenko Sci. Soc., Lviv (2007).
R. I. Asaro and D. M. Barnett, “The nonuniform transformation strain problem for an anisotropic ellipsoidal inclusion,” J. Mech. Phys. Solids, 23, No. 1, 77–83 (1975).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Fizyko-Khimichna Mekhanika Materialiv, Vol. 55, No. 6, pp. 26–31, November–December, 2019.
Rights and permissions
About this article
Cite this article
Sylovanyuk, V.P., Ivantyshyn, N.A. Healing of Cracks in Anisotropic Bodies. Mater Sci 55, 804–811 (2020). https://doi.org/10.1007/s11003-020-00373-6
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11003-020-00373-6