Global optimization based on active preference learning with radial basis functions

Abstract

This paper proposes a method for solving optimization problems in which the decision-maker cannot evaluate the objective function, but rather can only express a preference such as “this is better than that” between two candidate decision vectors. The algorithm described in this paper aims at reaching the global optimizer by iteratively proposing the decision maker a new comparison to make, based on actively learning a surrogate of the latent (unknown and perhaps unquantifiable) objective function from past sampled decision vectors and pairwise preferences. A radial-basis function surrogate is fit via linear or quadratic programming, satisfying if possible the preferences expressed by the decision maker on existing samples. The surrogate is used to propose a new sample of the decision vector for comparison with the current best candidate based on two possible criteria: minimize a combination of the surrogate and an inverse weighting distance function to balance between exploitation of the surrogate and exploration of the decision space, or maximize a function related to the probability that the new candidate will be preferred. Compared to active preference learning based on Bayesian optimization, we show that our approach is competitive in that, within the same number of comparisons, it usually approaches the global optimum more closely and is computationally lighter. Applications of the proposed algorithm to solve a set of benchmark global optimization problems, for multi-objective optimization, and for optimal tuning of a cost-sensitive neural network classifier for object recognition from images are described in the paper. MATLAB and a Python implementations of the algorithms described in the paper are available at http://cse.lab.imtlucca.it/~bemporad/glis.

1 Introduction

1.1 Learning and optimization from preferences

Taking an optimal decision is the process of selecting the value of certain variables that produces “best” results. When using mathematical programming to solve this problem, “best” means that the taken decision minimizes a certain cost function, or equivalently maximizes a certain utility function. However, in many problems an objective function is not quantifiable, either because it is of qualitative nature or because it involves several goals, whose relative importance is not well defined. Moreover, sometimes the “goodness” of a certain combination of decision variables can only be assessed by a human decision maker.

This situation arises in many practical cases. When calibrating the parameters of a deep neural network whose goal is to generate a synthetic painting or artificial music, artistic “beauty” is hardly captured by a numerical function, and a human decision-maker is required to assess whether a certain combination of parameters produces “beautiful” results. For example, Brochu et al. (2008) propose a tool to help digital artists to calibrate the parameters of an image generator so that the synthetic image “resembles” a given one. Another example is in industrial automation when calibrating the tuning knobs of a control system: based on engineering insight and rules of thumb, the task is usually carried out manually by trying a series of combinations until the calibrator is satisfied by the observed closed-loop performance. Another well-known example is A/B testing (Siroker and Koomen 2013), which aims at comparing two versions of a marketing asset to find which performs better. A frequent situation in which it is also hard to formulate an objective function is multi-objective optimization (Chinchuluun and Pardalos 2007). Here, selecting a-priori the correct weighted sum of the objectives to minimize in order to choose an optimal decision vector can be very difficult, and is often a human operator that needs to assess whether a certain Pareto optimal solution is better than another one, based on his or her (sometimes unquantifiable) feelings.

It is well known in neuroscience that humans are better at choosing between two options (“this is better than that”) than among multiple ones (Chau et al. 2014; Chernev et al. 2015). In consumer psychology, the “choice overload” effect shows that a human, when presented an abundance of options, has more difficulty to make a decision than if only a few options are given. On the other hand, having a large number of possibilities to choose from creates very positive feelings in the decision maker (Chernev et al. 2015). In economics, the difficulty of rational behavior in choosing the best option was also recognized in Simon (1955), due to the complexity of the decision problem exceeding the cognitive resources of the decision maker. The importance of focusing on discrete choices in psychology dates back at least to the 1920’s (Thurstone 1927).

Several authors have investigated algorithms to learn models that can predict the outcome of a preference query. In Hüllermeier et al. (2008) the authors classify four different ways of learning from preference information. They distinguish between modeling a utility function and modeling pairwise-preferences, and also between object ranking, i.e., learning how to rank a set of objects (Tesauro 1989; Cohen et al. 1999) and label ranking, i.e., learning (for a given instance) a preference relation between a finite set of labels (Har-Peled et al. 2002; Hüllermeier et al. 2008). In particular, the approach of Tesauro (1989) consists of training a neural-network architecture that, given the two samples to compare, predicts the outcome of the comparison. Consistency of comparisons is guarantee by a particular symmetry chosen for the architecture. Interestingly, the value of the final layer of the network corresponds to an absolute numerical score associated with the input sample, that can be reinterpreted as a utility value. The reader is referred to Wang (1994), Herbrich et al. (1998), Joachims (2002), Haddawy et al. (2003) for alternative methods to learn a utility function from pairwise-preferences.

Rather than learning a full preference model that, given any pair of objects (i.e., two vectors of decision variables), can predict the outcome of their comparison, in this paper we are interested in learning a model for the sole purpose of driving the search towards the most preferable object. In other words, rather than introducing a utility function as an instrument to model preferences, we want to maximize a (totally unknown) utility function from preference information, or equivalently to minimize an underlying objective function. The link between preferences and objective function can be simply stated as follows: given two decision vectors $x_1$, $x_2$, we say that $x_2$ is not “preferred” to $x_1$ if $f(x_1)\le f(x_2)$. Therefore, finding a global optimizer of f by preference information can be reinterpreted as the problem of looking for the vector $x^\star$ such that it is preferred to any other vector x. Such a preference-based optimization approach requires a solution method that only observes the outcome of the comparison $f(x_1)\le f(x_2)$, not the values $f(x_1),f(x_2)$, not even the value of the difference $f(x_1)-f(x_2)$.

1.2 Optimization of expensive black-box functions (not based on preferences)

Different methods were proposed in the global optimization literature for finding a global minimum of a function whose analytical expression is not available (black-box function) but can be evaluated, although the evaluation can be expensive (Rios and Sahinidis 2013). Some of the most successful methods rely on computing a simpler-to-evaluate surrogate of the objective function and use it to drive the search of new candidate optimizers to sample (Jones 2001). The surrogate is refined iteratively as new values of the actual objective function are collected at those points. Rather than minimizing the surrogate, which may easily lead to miss the global optimum of the actual objective function, an acquisition function is minimized instead to generate new candidates. The latter function consists of a combination of the surrogate and of an extra term that promotes exploring areas of the decision space that have not been yet sampled.

Bayesian Optimization (BO) is a very popular method exploiting surrogates to globally optimize functions that are expensive to evaluate. In BO, the surrogate of the underlying objective function is modeled as a Gaussian process (GP), so that model uncertainty can be characterized using probability theory and used to drive the search (Kushner 1964). BO is used in several methods such as Kriging (Matheron 1963), in Design and Analysis of Computer Experiments (DACE) (Sacks et al. 1989), material and drug design (Ueno et al. 2016; Pyzer-Knapp 2018), tuning of controllers (Piga et al. 2019), in the Efficient Global Optimization (EGO) algorithm (Jones et al. 1998), and is nowadays heavily used in machine learning for hyper-parameter tuning (Brochu et al. 2010).

Other methods for derivative-free optimization of expensive black-box functions are also available outside the BO literature (Ishikawa et al. 1999; Gutmann 2001; Regis and Shoemaker 2005). These approaches have the same rationale of Bayesian optimization, in the sense that they iteratively estimate a surrogate function fitting to the available observations of the objective function. The surrogate is then used (along with other terms promoting global search) to suggest the next query point. Bayesian optimization mainly differs from these methods as Bayesian inference is employed in BO to build the surrogate function, and its probability interpretation is used to select next query point.

The method proposed in this paper for preference-based optimization partially relies on the approach recently proposed by one of the authors in Bemporad (2020) for global optimization of known, but difficult to evaluate, functions. In Bemporad (2020), general radial basis functions (RBFs) are used to construct the surrogate, and inverse distance weighting (IDW) functions to promote exploration of the space of decision variables.

1.3 Preference-based optimization of expensive black-box function

As we assume that the function f is unknown, finding an optimal value of the decision variables that is “best”, in that the human operator always prefers it compared to all other tested combinations, may involve a lot of trial and error. For example, in parameter calibration the operator has to try many combinations before being satisfied with the winner one. Algorithms are therefore required that drive the trials by automatically proposing decision vectors to the operator for testing, so to converge to the best choice possibly within the least number of experiments.

In the derivative-free black-box global optimization literature there exist some methods for minimizing an objective function f that can be used also for preference-based optimization. For example particle swarm optimization (PSO) algorithms (Kennedy 2010; Vaz and Vicente 2007) drive the evolution of particles only based on the outcome of comparisons between function values and could be used in principle for preference-based optimization. However, although very effective in solving many complex global optimization problems, PSO is not conceived for keeping the number of evaluated preferences small, as it relies on randomness (of changing magnitude) in moving the particles, and would be therefore especially inadequate in solving problems where a human decision maker is involved in the loop to express preferences.

Therefore, optimization of expensive (unknown) black-box functions based only on preferences expressed by a user require specific approaches. In particular, active preference learning, in which the user is iteratively asked to express a preference between a paired comparison, have been proved a successful one.

Several algorithms were proposed in the literature for active preference learning. The survey paper (Busa-Fekete et al. 2018) presents an exhaustive review of different active learning algorithms proposed for multi-armed dueling bandit problems (Yue et al. 2012), where the goal is to find the most desirable choice from a finite set of possible options only based on pairwise preferences expressed by the user. Among others, we mention the methods based on Upper Confidence Bounds (Zoghi et al. 2014, 2015), Thompson Sampling (Yue and Joachims 2011; Wu and Liu 2016), and Minimum Empirical Divergence (Komiyama et al. 2015).

Algorithms for active preference learning were also developed in the field of reinforcement learning (see, e.g., Fürnkranz et al. 2012; Akrour et al. 2012; Wilson et al. 2012; Akrour et al. 2014; Christiano et al. 2017), for situations in which the quantitative evaluation of the reward function is not available, and the policy is learned only based a qualitative evaluation of the agent’s behavior expressed by the user in terms of preferences.

Bayesian optimization has been also adapted for preference-based optimization of expensive (unknown) black-box functions (Chu and Ghahramani 2005a; Brochu et al. 2008; González et al. 2017; Abdolshah et al. 2019). In these works, the surrogate function describing the observed set of preferences is described in terms of a GP, using a probit model to describe the observed pairwise preferences (Chu and Ghahramani 2005b). The posterior distribution of the latent function is then approximated (e.g., using Laplace’s method or Expectation Propagation). This approximation provides a probabilistic prediction of the preference that is used to define an acquisition function (like expected improvement) which is maximized in order to select the next query point. As in standard Bayesian optimization, the acquisition function used in Bayesian preference automatically balances exploration (selecting queries with high uncertainty on the preference) and exploitation (selecting queries which are expected to lead to improvements in the objective function).

Successful applications of active preference learning include optimal scheduling of calenders shared by multiple users (Gervasio et al. 2005), medical applications such as recovering motor function after a spinal-cord injury (Sui and Burdick 2014; Sui et al. 2017), semi-automated calibration of optimal controllers (Zhu et al. 2020), and robotics (Wilde et al. 2020a; Sadigh et al. 2017; Wilde et al. 2020b), just to cite a few.

1.4 Contribution

In this paper we propose a new approach for optimization based on active preference learning in which the surrogate function is modeled by RBFs. The surrogate function only needs to satisfy, if possible, the preferences already expressed by the decision maker at sampled points. The weights of the RBFs defining the surrogate are computed by solving a linear or quadratic programming problem aiming at satisfying the available training set of pairwise preferences. The training dataset of the surrogate function is actively augmented in an incremental way by the proposed algorithm according to two alternative criteria. The first criterion, similarly to Bemporad (2020), is based on a trade off between minimizing the surrogate and maximizing the distance from existing samples using IDW functions. The second alternative criterion is based on quantifying the probability of getting an improvement based on a maximum-likelihood interpretation of the RBF weight selection problem, which allows quantifying the probability of getting an improvement based on the surrogate function. Based on one of the above criteria, the proposed algorithm constructs an acquisition function that is very cheap to evaluate and is minimized to generate a new sample and to query a new preference.

Compared to preferential Bayesian optimization (PBO), the proposed approach is computationally lighter, due to the fact that computing the surrogate simply requires solving a convex quadratic or linear programming problem. Instead, in PBO one has to first compute the Laplace approximation of the posterior distribution of the preference function, which requires to calculate (via a Newton–Raphson numerical optimization algorithm) the mode of the posterior distribution, and then solve a system of linear equations, whose size is equal to the number of observations. Moreover, the IDW term used by our approach to promote exploration does not depend on the surrogate, which guarantees that the space of optimization variables is well explored even if the surrogate poorly approximates the underlying preference function.

Overall, our formulation does not require to derive posterior probability distributions, with the advantage that (1) it can be more easily generalized than PBO, for example additional constraints on the surrogate function can be immediately taken into account in the convex programming problem that might not have a probabilistic interpretation; (2) in particular the RBF+IDW version of the method is purely deterministic and delivers a similar level of performance with an easier interpretation than PBO; (3) the method does not require approximating posteriors that cannot be computed analytically and hence may result computationally involved. Such advantages do not compromise the performance of the algorithm in determining the best solution: compared to PBO that uses Laplace approximation of the posterior, within the same number of queried preferences our algorithm often achieves a better quality solution, as we will show in a set of benchmarks used in global optimization and in solving a multi-objective optimization problem.

1.5 Outline

The paper is organized as follows. In Sect. 2 we formulate the preference-based optimization problem we want to solve. Section 3 proposes the way to construct the surrogate function using linear or quadratic programming and Sect. 4 the acquisition functions that are used for generating new samples. The active preference learning algorithm is stated in Sect. 5 and its possible application to solve multi-objective optimization problems in Sect. 6. Section 7 presents numerical results obtained in applying the preference learning algorithm for solving a set of benchmark global optimization problems, a multi-objective optimization problem, and for optimal tuning of a cost-sensitive neural network classifier for object recognition from images. Finally, some conclusions are drawn in Sect. 8.

A MATLAB and a Python implementation of the proposed approach is available for download at http://cse.lab.imtlucca.it/ bemporad/glis.

2 Problem statement

Given two vectors $x_1,x_2\in {{\mathbb {R}}}^n$ of decision variables, consider the preference function $\pi :{{\mathbb {R}}}^n\times {{\mathbb {R}}}^n\rightarrow \{-1,0,1\}$ defined as

$$\begin{aligned} \pi (x_1,x_2)=\left\{ \begin{array}{ll} -1 &{}\hbox {if }x_1\hbox { ``better'' than }x_2\\ 0 &{}\hbox {if }x_1\hbox { ``as good as'' }x_2\\ 1 &{}\hbox {if }x_2\hbox { ``better'' than }x_1 \end{array}\right. \end{aligned}$$

where for all $x_1,x_2\in {{\mathbb {R}}}^n$ it holds $\pi (x_1,x_1)=0$, $\pi (x_1,x_2)=-\pi (x_2,x_1)$, and the transitive property

$$\begin{aligned} \pi (x_1,x_2) = \pi (x_2,x_3)=-1\ \Rightarrow \pi (x_1,x_3) = -1 \end{aligned}$$

Moreover, assume that we are interested in searching for decision vectors with values within lower and upper bounds $\ell ,u\in {{\mathbb {R}}}^n$ and within the set

$$\begin{aligned} {\mathcal {X}}=\{x\in {{\mathbb {R}}}^n:\ g(x)\le 0\} \end{aligned}$$

(1)

where $q\ge 0$ is the number of constraints defining ${\mathcal {X}}$, $g:{{\mathbb {R}}}^n\rightarrow {{\mathbb {R}}}^q$, and ${\mathcal {X}}={{\mathbb {R}}}^n$ when $q=0$ (no inequality constraint is enforced). We assume that the function g defining the condition $x\in {\mathcal {X}}$ in (1) is known. For example, in case of linear inequality constraints we have $g(x)=Ax-b$, $A\in {{\mathbb {R}}}^{q\times n}$, $b\in {{\mathbb {R}}}^q$, $q\ge 0$. We exclude equality constraints $A_{e}x=b_e$, as they can be eliminated by reducing the number of decision variables.

The objective of this paper is to solve the following constrained global optimization problem:

$$\begin{aligned} \hbox {find}\ x^\star \ \hbox {such that}\ \pi (x^\star ,x)\le 0,\ \forall x\in {\mathcal {X}},\ \ell \le x\le u \end{aligned}$$

(2)

that is to find the vector $x^\star \in {{\mathbb {R}}}^n$ of decision variables that is “better” (or “no worse”) than any other vector $x\in {{\mathbb {R}}}^n$ according to the preference function $\pi$ within the given admissible set.

The problem of minimizing an objective function $f:{{\mathbb {R}}}^n\rightarrow {{\mathbb {R}}}$ under constraints,

$$\begin{aligned} \begin{array}{rcrl} x^\star &{}&={}\arg {\min }_x&{} f(x)\\ &{} &{}\mathrm{s.t.}&{} \ell \le x\le u\\ &{} &{} &{}x\in {\mathcal {X}}\end{array} \end{aligned}$$

can be written as in (2) by defining

$$\begin{aligned} \pi (x_1,x_2)=\left\{ \begin{array}{ll} -1 &{}\hbox {if }f(x_1)<f(x_2)\\ 0 &{}\hbox {if }f(x_1)=f(x_2)\\ 1 &{}\hbox {if }f(x_1)>f(x_2) \end{array}\right. \end{aligned}$$

(3)

In this paper we assume that we do not have a way to evaluate the objective function f. The only assumption we make is that for each given pair of decision vectors $x_1,x_2\in {\mathcal {X}}$, $\ell \le x\le u$, only the value $\pi (x_1,x_2)$ is observed. The rationale of our problem formulation is that often one encounters practical decision problems in which a function f is impossible to quantify, but anyway it is possible to express a preference, for example by a human operator, for any given presented pair $(x_1, x_2)$. The goal of the preference-based optimization algorithm proposed in this paper is to suggest iteratively a sequence of samples $x_1,\ldots ,x_N$ to test and compare such that $x_N$ approaches $x^\star$ as N grows.

In what follows we implicitly assume that a function f actually exists but is completely unknown, and attempt to synthesize a surrogate function ${\hat{f}}:{{\mathbb {R}}}^n\rightarrow {{\mathbb {R}}}$ of f such that its associated preference function ${\hat{\pi }}:{{\mathbb {R}}}^n\times {{\mathbb {R}}}^n\rightarrow \{-1,0,1\}$ defined as in (3) coincides with $\pi$ on the finite set of sampled pairs of decision vectors.

3 Surrogate function

Assume that we have generated $N\ge 2$ samples $X=\{x_1\ \ldots \ x_N\}$ of the decision vector, with $x_i,x_j\in {{\mathbb {R}}}^n$ such that $x_i\ne x_j$, $\forall i\ne j$, $i,j=1,\ldots ,N$, and have evaluated a preference vector $B=[b_1\ \ldots \ b_{M}]'\in \{-1,0,1\}^{M}$

$$\begin{aligned} b_h=\pi (x_{i(h)},x_{j(h)}) \end{aligned}$$

(4)

where M is the number of expressed preferences, $1 \le M \le \left( {\begin{array}{c}N\\ 2\end{array}}\right)$, $h\in \{1,\ldots ,M\}$, $i(h), j(h)\in \{1,\ldots ,N\}$, $i(h) \ne j(h)$.

In order to find a surrogate function ${\hat{f}}:{{\mathbb {R}}}^{n} \rightarrow {{\mathbb {R}}}$ such that

$$\begin{aligned} \pi (x_{i(h)},x_{j(h)}) = {\hat{\pi }}(x_{i(h)},x_{j(h)}),\ \forall h=1,\ldots ,M \end{aligned}$$

(5)

where ${\hat{\pi }}$ is defined from ${\hat{f}}$ as in (3), we consider a surrogate function ${\hat{f}}$ defined as the following radial basis function (RBF) interpolant (Gutmann 2001; McDonald et al. 2007)

$$\begin{aligned} {\hat{f}}(x)=\sum _{i=1}^N\beta _i\phi (\epsilon d(x,x_i)) \end{aligned}$$

(6)

In (6) function $d:{{\mathbb {R}}}^{n}\times {{\mathbb {R}}}^{n}\rightarrow {{\mathbb {R}}}$ is the squared Euclidean distance

$$\begin{aligned} d(x_1,x_2)=\Vert x_1-x_2\Vert _2^2,\ x_1,x_2\in {{\mathbb {R}}}^n \end{aligned}$$

$\epsilon >0$ is a scalar parameter, $\phi :{{\mathbb {R}}}\rightarrow {{\mathbb {R}}}$ is a RBF, and $\beta _i$ are coefficients that we determine as explained below. Examples of RBFs are $\phi (\epsilon d)=\frac{1}{1+(\epsilon d)^2}$ (inverse quadratic), $\phi (\epsilon d)=e^{-(\epsilon d)^2}$ (Gaussian), $\phi (\epsilon d)=(\epsilon d)^2\log (\epsilon d)$ (thin plate spline), see more examples in Gutmann (2001); Bemporad (2020).

In accordance with (5), we impose the following preference conditions

$$\begin{aligned} \begin{array}{ll} {\hat{f}}(x_{i(h)})\le {\hat{f}}(x_{j(h)})-\sigma +\varepsilon _h,&{} \forall h=1,\ldots ,M\ \hbox {such that}\ \pi (x_{i(h)},x_{j(h)})=-1\\ {\hat{f}}(x_{i(h)})\ge {\hat{f}}(x_{j(h)})+\sigma -\varepsilon _h,&{} \forall h=1,\ldots ,M\ \hbox {such that}\ \pi (x_{i(h)},x_{j(h)})=1\\ |{\hat{f}}(x_{i(h)})-{\hat{f}}(x_{j(h)})|\le \sigma +\varepsilon _h,&{} \forall h=1,\ldots ,M\ \hbox {such that}\ \pi (x_{i(h)},x_{j(h)})=0 \end{array} \end{aligned}$$

(7)

where $\sigma >0$ is a given tolerance and $\varepsilon _h$ are slack variables, $\varepsilon _h\ge 0$, $h=1,\ldots ,M$.

Accordingly, the coefficient vector $\beta =[\beta _1\ \ldots \ \beta _N]'$ is obtained by solving the following convex optimization problem

$$\begin{aligned} \begin{array}{rll} \min _{\beta ,\varepsilon } &{}\displaystyle {\sum _{h=1}^{M} c_h\varepsilon _h+\frac{\lambda }{2}\sum _{k=1}^N\beta _{k}^2 }\\ \mathrm{s.t.}&{} \displaystyle {\sum _{k=1}^N\left (\phi \left( \epsilon d(x_{i(h)},x_{k})\right) -\phi \left( \epsilon d(x_{j(h)},x_{k})\right) \right )\beta _k\le -\sigma +\varepsilon _h},&{} \forall h:\ b_h=-1\\ &{}\displaystyle {\sum _{k=1}^N\left (\phi \left( \epsilon d(x_{i(h)},x_{k})\right) -\phi \left( \epsilon d(x_{j(h)},x_{k})\right) \right )\beta _k\ge \sigma -\varepsilon _h},&{} \forall h:\ b_h=1\\ &{}\displaystyle {\sum _{k=1}^N\left (\phi \left( \epsilon d(x_{i(h)},x_{k})\right) -\phi \left( \epsilon d(x_{j(h)},x_{k})\right) \right )\beta _k\le \sigma +\varepsilon _h},&{} \forall h:\ b_h=0\\ &{}\displaystyle {\sum _{k=1}^N\left (\phi \left( \epsilon d(x_{i(h)},x_{k})\right) -\phi \left( \epsilon d(x_{j(h)},x_{k})\right) \right )\beta _k\ge -\sigma -\varepsilon _h},&{} \forall h:\ b_h=0\\ &{} h=1,\ldots ,M \end{array} \end{aligned}$$

(8)

where $c_h$ are positive weights, for example $c_h=1$, $\forall h=1,\ldots ,M$. The scalar $\lambda$ is a regularization parameter. When $\lambda >0$ problem (8) is a quadratic programming (QP) problem that, since $c_h>0$ for all $h=1,\ldots ,M$, admits a unique solution. If $\lambda =0$ problem (8) becomes a linear program (LP), whose solution may not be unique.

The use of slack variables $\varepsilon _h$ in (8) allows one to relax the constraints imposed by the specified preference vector B. Constraint infeasibility might be due to an inappropriate selection of the RBF and/or to outliers in the acquired components $b_h$ of vector B. The latter condition may easily happen when preferences $b_h$ are expressed by a human decision maker (or by different decision makers) in an inconsistent way. Since each slack variable $\varepsilon _h$ is multiplied by a positive weight $c_h$, an (optional) “degree of confidence” $\mu _h$ can be associated with the outcome $b_h$ of the query, where small $\mu _h$ means low confidence, a high $\mu _h$ means high confidence. According to this interpretation of the “degree of confidence” $\mu _h$, the user can define the weights $c_h$ as inversely proportional to $\mu _h$, for example by setting $c_h=\frac{1}{\mu _h}$.

For a given set $X=\{x_1\ \ldots \ x_N\}$ of samples, setting up (8) requires computing the $N\times N$ symmetric matrix $\varPsi$ whose (i, j)-entry is

$$\begin{aligned} \varPsi _{ij}=\phi (\epsilon d(x_i,x_j)) \end{aligned}$$

with $\varPsi _{ii}=1$ for the inverse quadratic and Gaussian RBF, while for the thin plate spline RBF $\varPsi _{ii}=\lim _{d\rightarrow 0}\phi (\epsilon d)=0$. Note that if a new sample $x_{N+1}$ is collected, updating matrix $\varPsi$ only requires computing $\phi (d(x_{N+1},x_j),\epsilon )$ for all $j=1,\ldots ,N+1$.

Fig. 1

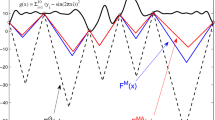
Example of surrogate function ${\hat{f}}$ (middle plot) based on preferences resulting from function f (top plot, blue) as in (9). Pairs of samples generating comparisons are connected by a green line. IDW exploration function z (bottom plot)

An example of surrogate function ${\hat{f}}$ constructed based on preferences generated as in (3) by the following scalar function (Bemporad 2020)

$$\begin{aligned} f(x)=\left( 1+\frac{x\sin (2x)\cos (3x)}{1+x^2}\right) ^2+\frac{x^2}{12}+\frac{x}{10} \end{aligned}$$

(9)

is depicted in Fig. 1. The surrogate is generated from $N=6$ samples by solving the LP (8) ($\lambda =0$) with matrix $\varPsi$ generated by the inverse quadratic RBF with $\epsilon =2$ and $\sigma =\frac{1}{N}$.

3.1 Self-calibration of RBF

Computing the surrogate ${\hat{f}}$ requires choosing the hyper-parameter $\epsilon$ defining the shape of the RBF $\phi$ (Eq. (6)), thus influencing the capability of the resulting surrogate model of capturing the latent objective function. Therefore, as typical in machine learning for hyper-parameter tuning, we adapt $\epsilon$ through K-fold cross-validation (Stone 1974), by splitting the M available pairwise comparisons into K (nearly equally sized) disjoint subsets. To this end, let us define the index sets ${\mathcal {S}}_{i}$, $i=1,\ldots ,K$, such that $\cup _{i=1}^K{\mathcal {S}}_{i}=\{1,\ldots ,M\}$, ${\mathcal {S}}_{i} \cap {\mathcal {S}}_{j} = \emptyset$, for all $i,j=1,\ldots ,K$, $i\ne j$. For a given $\epsilon$ and for all $i=1,\ldots ,K$, the preferences indexed by the set $\{1,\ldots ,M\} \setminus {\mathcal {S}}_{i}$ are used to fit the surrogate function ${\hat{f}}_\epsilon$ by solving (8), while the performance of ${\hat{f}}_\epsilon$ in predicting comparisons indexed by ${\mathcal {S}}_{i}$ is quantified in terms of number of correctly classified preferences ${\mathcal {C}}_i(\epsilon )=\sum _{h \in {\mathcal {S}}_{i}} \eta _h(\epsilon )$, where $\eta _h(\epsilon )=1$ if $\pi (x_{i(h)},x_{j(h)}) = {\hat{\pi _\epsilon }}(x_{i(h)},x_{j(h)})$ or 0 otherwise, and ${\hat{\pi _\epsilon }}$ is the preference function induced by ${\hat{f}}_\epsilon$ as in (3). Since the hyper-parameter $\epsilon$ is scalar, a fine grid search can be used to find the value of $\epsilon$ maximizing $\sum _{i=1}^K{\mathcal {C}}_i(\epsilon )$.

Since in active preference learning the number M of observed pairwise preferences is usually small, we use ${\mathcal {S}}_{h}=\{h\}$, $h=1,\ldots ,M$, namely M-fold cross validation or leave-one-out, to better exploit the M available comparisons.

Let $x^\star _N\in {{\mathbb {R}}}^n$ be the best vector of decision variables in the finite set $X=\{x_1,\ldots ,x_N\}$, corresponding to the smallest index $i^\star$ such that

$$\begin{aligned} \pi (x_{i^\star },x_i)\le 0,\ \forall i=1,\ldots ,N \end{aligned}$$

(10)

Since in active preference learning one is mostly interested in correctly predicting the preference w.r.t. the best optimal point $x^\star _N$, the solution of problem (8) and the corresponding score ${\mathcal {C}}_i(\epsilon )$ are not computed for all indexes h such that $x_{i(h)}=x^\star _N$, that is the preferences involving $x^\star _N$ are only used for training and not for testing.

For a given value of the hyper-parameter $\epsilon$, the K-fold cross-validation procedure for self-calibration requires to formulate and solve problem (8) K times ($M=N-1$ times in case of leave-one-out cross validation, or less when comparisons involving $x_N^\star$ are only used for training). As $\epsilon$ is a scalar value, the complexity trivially scales linearly with the number of values of $\epsilon$ for which the K-fold cross-validation procedure is executed. In order to reduce computations, we execute the self-calibration procedure and change $\epsilon$ only at a subset ${\mathcal {I}}_{\mathrm{{sc}}} \subseteq \{1,\ldots ,N_{\mathrm{max}}-1\}$ of iterations.

4 Acquisition function

Let $x^\star _N\in {{\mathbb {R}}}^n$ be the best vector of decision variables defined in (10). Consider the following procedure: (i) generate a new sample by pure minimization of the surrogate function ${\hat{f}}$ defined in (6),

$$\begin{aligned} x_{N+1}=\arg \min {\hat{f}}(x)\ \mathrm{s.t.}\ \ell \le x\le u,\ x\in {\mathcal {X}}\end{aligned}$$

with $\beta$ obtained by solving the LP (8), (ii) evaluate $\pi (x_{N+1},x^\star _N)$, (iii) update ${\hat{f}}$, and (iv) iterate over N. Such a procedure may easily miss the global minimum of (2), a phenomenon that is well known in global optimization based on surrogate functions: purely minimizing the surrogate function may lead to converge to a point that is not the global minimum of the original function (Jones 2001; Bemporad 2020). Therefore, the exploitation of the surrogate function ${\hat{f}}$ is not enough to look for a new sample $x_{N+1}$, but also an exploration objective must be taken into account to probe other areas of the feasible space. Such a balance between exploration and exploitation is addressed by defining a proper acquisition function $a:{{\mathbb {R}}}^n\rightarrow {{\mathbb {R}}}$, which is minimized instead of the surrogate function ${\hat{f}}(x)$. In the next paragraphs we propose two different acquisition functions that can be used to define the new sample $x_{N+1}$ to compare the current best sample $x^\star _N$ to.

4.1 Acquisition based on inverse distance weighting (IDW)

Following the approach suggested in Bemporad (2020), we construct an exploration function using ideas from inverse distance weighting (IDW). Consider the IDW exploration function $z:{{\mathbb {R}}}^n\rightarrow {{\mathbb {R}}}$ defined by

$$\begin{aligned} z(x)=\left\{ \begin{array}{ll} 0 &{} \hbox {if}\ x\in \{x_1,\ldots ,x_N\}\\ \tan ^{-1}\left( \frac{1}{\sum _{i=1}^Nw_i(x)}\right) &{} \hbox {otherwise}\end{array}\right. \end{aligned}$$

(11)

where $w_i:{{\mathbb {R}}}^n\rightarrow {{\mathbb {R}}}$ is defined by Shepard (1968)

$$\begin{aligned} w_i(x)=\frac{1}{d^2(x,x_i)} \end{aligned}$$

Clearly $z(x_i)=0$ for all $x_i\in X$ (namely, for all inputs $x_i$ already sampled), and $z(x)>0$ in ${{\mathbb {R}}}^n\setminus X$. Fig. 1 shows the IDW exploration function z obtained from (11) for the example generated from (9). Note that the IDW exploration function z(x) increases for inputs x far away from the sampled inputs X. Thus, maximization of z(x) promotes sampling in unexplored regions of the input space. The arc tangent function in (11) avoids that z(x) gets excessively large far away from all sampled points.

Given an exploration parameter $\delta \ge 0$, the acquisition function a is defined as

$$\begin{aligned} a(x)=\frac{{\hat{f}}(x)}{\varDelta {\hat{F}}}-\delta z(x) \end{aligned}$$

(12)

where

$$\begin{aligned} \varDelta {\hat{F}}=\max _i\{{\hat{f}}(x_i)\}-\min _i\{{\hat{f}}(x_i)\} \end{aligned}$$

is the range of the surrogate function on the samples in X. By setting

$$\begin{aligned} y=\varPsi \beta \end{aligned}$$

we get ${\hat{f}}(x_i)=y_i$, $\forall i=1,\ldots ,N$, and therefore

$$\begin{aligned} \varDelta {\hat{F}} = \max (y)-\min (y) \end{aligned}$$

Clearly $\varDelta {\hat{F}} \ge \sigma$ if at least one comparison $b_h=\pi (x_{i(h)},x_{i(h)}) \ne 0$. The scaling factor $\varDelta {\hat{F}}$ is used to simplify the choice of the exploration parameter $\delta$.

The following lemma immediately derives from Bemporad (2020, Lemma 2):

Lemma 1

Function a is differentiable everywhere on ${{\mathbb {R}}}^n$.

As we will detail below, given a set X of N samples $\{x_1,\ldots ,x_N\}$ and a vector B of preferences defined by (4), the next sample $x_{N+1}$ is defined by solving the global optimization problem

$$\begin{aligned} x_{N+1}=\arg \min _{\ell \le x\le u,\ x\in {\mathcal {X}}} a(x) \end{aligned}$$

(13)

Problem (13) can be solved very efficiently using various global optimization techniques, either derivative-free (Rios and Sahinidis 2013) or, if ${\mathcal {X}}=\{x: g(x)\le 0\}$ and g is also differentiable, derivative-based. In case some components of vector x are restricted to be integer, (13) can be solved by mixed-integer programming.

4.2 Acquisition based on probability of improvement (PI)

In this section, we show how the surrogate function ${\hat{f}}$ derived by solving problem (8) can be seen as a maximum-likelihood estimate of an appropriate probabilistic model. This will allow us to define an alternative acquisition function based on the probability of improvement (PI) with respect to the current best solution. The analyses described in the following are inspired by the probabilistic interpretation of support vector machines described in Franc et al. (2011).

Let $\lambda >0$ and let $\varPhi (\epsilon ,X,x_{i(h)},x_{j(h)})$ be the N-dimensional vector obtained by collecting the terms $\phi (\epsilon d( x_{i(h)},x_k))-\phi (\epsilon d( x_{j(h)},x_k))$, with $h=1,\ldots ,M$, $k=1,\ldots ,N$.

Let us rewrite the QP problem (8) without the slack variables $\varepsilon _i$ as

$$\begin{aligned} \begin{array}{rll} {\displaystyle \min _{\beta }}&{\displaystyle \sum _{h=1}^{M}} c_{h} \ell _{b_h}(\varPhi (\epsilon ,X,x_{i(h)},x_{j(h)})'\beta )+ \frac{\lambda }{2} \left\| \beta \right\| ^2 \end{array} \end{aligned}$$

(14)

where

$$\begin{aligned} \ell _{-1}(\varPhi (\epsilon ,X,x_{i(h)},x_{j(h)})'\beta ) &=\max \{0, \varPhi (\epsilon ,X,x_{i(h)},x_{j(h)})'\beta + \sigma ) \} \end{aligned}$$

(15a)

$$\begin{aligned} \ell _{1}(\varPhi (\epsilon ,X,x_{i(h)},x_{j(h)})'\beta ) &=\max \{0;-\varPhi (\epsilon ,X,x_{i(h)},x_{j(h)})'\beta + \sigma \} \end{aligned}$$

(15b)

$$\begin{aligned} \ell _{0}( \varPhi (\epsilon ,X,x_{i(h)},x_{j(h)})'\beta ) &=\max \{0, \pm \varPhi (\epsilon ,X,x_{i(h)},x_{j(h)})'\beta - \sigma \} \end{aligned}$$

(15c)

are piecewise linear convex functions of $\beta$, for all $h=1,\ldots ,M$.

Theorem 1

For a given hyper-parameter $\lambda >0$, let $\beta (\lambda )$ be the minimizer of problem (14) and let $\tau (\lambda ) = \left\| \beta (\lambda )\right\|$. Then vector $u^\star =\frac{\beta (\lambda )}{\tau (\lambda )}$ is the minimizer of the following problem

$$\begin{aligned} \min _{u: \Vert u\Vert =1} \sum _{h=1}^{M} c_{h} \ell _{b_h}(\tau (\lambda )\varPhi (\epsilon ,X,x_{i(h)},x_{j(h)})'u) \end{aligned}$$

(16)

Proof

See Appendix. $\square$

Theorem 1 thus provides a relation between the solution of the unconstrained regularized optimization problem (14) and the constrained, non-regularized, optimization problem (16). This allows us to focus on problem (16) instead of problem (14) (or equivalently, instead of the original QP problem (8)).

In order to avoid heavy notation, in the following we restrict the coefficients $c_h$ in (8) such that they are equal when the preference $b_h$ is the same, that is $c_h={\bar{c}}_{b_h}$ where ${\bar{c}}_{-1},{\bar{c}}_0,{\bar{c}}_{1}$ are given positive weights.

Let us now focus on problem (16) and consider the joint p.d.f.

$$\begin{aligned} p(\varPhi ,t;{\bar{c}},\tau ,u) = Z({\bar{c}},\tau ,u)e^{-{\bar{c}}_{t}\ell _{t}(\tau \varPhi 'u)} \kappa (\varPhi ), \end{aligned}$$

(17)

defined for $\varPhi \in {\mathbb {R}}^N$ and $t\in \{-1,0,1\}$, and parametrized by ${\bar{c}}=[{\bar{c}}_{-1}\ {\bar{c}}_0\ {\bar{c}}_1]'$, a strictly positive scalar $\tau$, and a generic unit vector u.

The distribution (17) is composed by three terms. The first term $Z({\bar{c}},\tau ,u)$ is a normalization constant. We will show next that $Z({\bar{c}},\tau ,u)$ does not depend on u when we restrict $\Vert u\Vert =1$. The second term $e^{-{\bar{c}}_{t}\ell _{t}(\tau \varPhi 'u)}$ depends on all the parameters $({\bar{c}},\tau ,u)$ and it is related to the objective function minimized in (16). The last term $\kappa (\varPhi )$ ensures integrability of $p(\varPhi ,t;{\bar{c}},\tau ,u)$ and that the normalization constant Z does not depend on u, as discussed next. A possible choice for $\kappa$ is $\kappa (\varPhi )=e^{-\varPhi '\varPhi }$.

The normalization constant Z in (17) guarantees that $p(\varPhi ,t;{\bar{c}},\tau ,u)$ is a probability density function, and thus it computed as

$$\begin{aligned} Z({\bar{c}},\tau ,u) = \frac{1}{\sum _{t\in \{-1,0,1\}}I_t({\bar{c}}_t,\tau ,u)} \end{aligned}$$

where for $t\in \{-1,0,1\}$ the term $I_t({\bar{c}}_t,\tau ,u)$ is the integral defined as

$$\begin{aligned} I_t({\bar{c}}_t,\tau ,u) = \int _{ \varPhi \in {\mathbb {R}}^N} e^{-{\bar{c}}_{t}\ell _{t}(\tau \varPhi 'u)}\kappa (\varPhi ) d\varPhi \end{aligned}$$

(18)

The following Theorem shows that $I_t({\bar{c}}_t,\tau ,u)$ does not depend on u, and so $Z({\bar{c}},\tau ,u)$ is also independent of u.

Theorem 2

Let $\kappa (\varPhi )$ in (17) be $\kappa (\varPhi )=e^{-\varPhi '\varPhi }$. For any $t \in \{-1, 0, 1\}$,

$$\begin{aligned} I_t({\bar{c}}_t,\tau ,u) = I_t({\bar{c}}_t,\tau ,{\bar{u}}) \ \ \forall u,{\bar{u}}: \Vert u\Vert =\Vert {\bar{u}}\Vert =1. \end{aligned}$$

Proof

See Appendix. $\square$

Because of Theorem 2, since now on, when we restrict $\Vert u\Vert =1$, we will drop the dependence on u of $Z({\bar{c}},\tau ,u)$ and simply write $Z({\bar{c}},\tau )$.

Let us assume that the samples of the training sequence $\{\varPhi (\epsilon ,X,h),b_h\}_{h=1}^M$ are i.i.d. and generated from the joint distribution $p(\varPhi ,t;{\bar{c}},\tau ,u)$ defined in (17). The negative log of the probability of the dataset $\{\varPhi (\epsilon ,X,x_{i(h)},x_{j(h)}),b_h\}_{h=1}^M$ given ${\bar{c}},\tau ,u$ is

$$\begin{aligned} L({\bar{c}},\tau ,u) &=-\sum _{h=1}^{M}\log p(\varPhi (\epsilon ,X,x_{i(h)}, x_{j(h)}),b_h;{\bar{c}},\tau ,u) = \\ &=-M\log Z({\bar{c}},\tau ) - \sum _{h=1}^{M} \log \kappa (\varPhi (\epsilon ,X,x_{i(h)},x_{j(h)}))\\&\quad + \sum _{h=1}^{M} {\bar{c}}_{b_h}\ell _{b_h}(\tau \varPhi (\epsilon ,X,x_{i(h)},x_{j(h)})'u) \end{aligned}$$

Thus, for fixed values of ${\bar{c}}$ and $\tau =\Vert \beta (\lambda )\Vert$, by Theorem 1 the minimizer $u^\star _L(\lambda )$ of

$$\begin{aligned} \min _{u:\ \Vert u\Vert =1}L({\bar{c}},\tau (\lambda ),u) \end{aligned}$$

is $u^\star _L=\frac{\beta (\lambda )}{\tau (\lambda )}$. In other words, for any fixed $\lambda >0$, the solution $\beta (\lambda )$ of the QP problem (8) can be reinterpreted as $\tau$ times the maximizer $u^\star _L(\lambda )$ of the joint likelihood $L({\bar{c}},\tau ,u)$ with respect to u, $\Vert u\Vert =1$, when $\tau =\Vert \beta (\lambda )\Vert$.

It is interesting to note that the marginal p.d.f. derived from the probabilistic model (17) is equal to

$$\begin{aligned} p(\varPhi ;{\bar{c}},\tau ,u) = \sum _{t=-1,0,1} p(\varPhi ,t;{\bar{c}},\tau ,u)= Z({\bar{c}},\tau )\kappa (\varPhi )\sum _{t=-1,0,1}e^{-{\bar{c}}_{t}\ell _{t}(\tau \varPhi 'u)} \end{aligned}$$

and therefore the corresponding preference posterior probability is

$$\begin{aligned} p(t|\varPhi ;{\bar{c}},\tau ,u) = \frac{p(\varPhi ,t;{\bar{c}},\tau ,u)}{p(\varPhi ;{\bar{c}},\tau ,u)} = \frac{ e^{-{\bar{c}}_{t}\ell _{t}(\varPhi '\beta )}}{\displaystyle {\sum _{t=-1,0,1}e^{-{\bar{c}}_{t}\ell _{t}( \varPhi '\beta )}}} \end{aligned}$$

(19)

where $\beta =\tau u$.

The preference posterior probability given in (19) can be used now to explore the vector space ${{\mathbb {R}}}^n$ and to define an alternative acquisition function, as described next.

Let $\beta$ be the vector obtained by solving (8) with N samples and M preferences. Let us treat again $x_{N+1}$ as a free sample x to optimize and consider (19) also for the new generic $(M+1)\hbox {th}$ comparison

$$\begin{aligned} \varPhi (\epsilon ,X,x,x^\star (N))=\left[ \begin{array}{c} \phi (\epsilon d(x,x_1)) -\phi (\epsilon d(x^\star _N,x_1)\\ \ldots \\ \phi (\epsilon d(x,x_N))-\phi (\epsilon d(x^\star _N,x_N) \end{array}\right] \end{aligned}$$

A criterion to choose $x_{N+1}$ is to maximize the preference posterior probability of obtaining a “better” sample compared to the current “best” sample $x^\star _N$ given by (19), or equivalently of getting $\pi (x_{N+1},x^\star _N)=-1$. This can be achieved by the following acquisition function

$$\begin{aligned} a(x)&=-p\left( t=-1\left| \varPhi (\epsilon ,X,x,x^\star _N); {\bar{c}},\Vert \beta \Vert ,\frac{\beta }{\Vert \beta \Vert }\right. \right) \nonumber \\ &=-\frac{ e^{-{\bar{c}}_{-1}\ell _{-1}(\varPhi (\epsilon ,X,x,x^\star _N)'\beta )}}{\displaystyle {\sum _{t=-1,0,1}e^{-{\bar{c}}_{t}\ell _{t}( \varPhi (\epsilon ,X,x,x^\star _N)'\beta )}}} \end{aligned}$$

(20)

Fig. 2

Example of acquisition functions a based on preferences resulting from function f as in (9) and Fig. 1. Top plot: RBF+IDW acquisition function a as in (12) with $\delta =1$ and $\delta =2$. Bottom plot: RBF+PI acquisition function a as in (20) based in probability of improvement. The minimum of a is highlighted with a diamond

Examples of acquisition functions a constructed based on preferences generated by the function f defined in (9) are depicted in Fig. 2, based on the same setting as in Fig. 1.

4.3 Scaling

Different components $x^j$ of x may have different upper and lower bounds $u^j$, $\ell ^j$. Rather than using weighted distances as in stochastic process model approaches such as Kriging methods (Sacks et al. 1989; Jones et al. 1998), we simply rescale the variables in optimization problem (2) to range in $[-1,1]$. As described in Bemporad (2020), we first tighten the given range $B_{\ell ,u}=\{x\in {{\mathbb {R}}}^n: \ell \le x\le u\}$ by computing the bounding box $B_{\ell _s,u_s}$ of the set $\{x\in {{\mathbb {R}}}^n:\ x\in {\mathcal {X}}\}$ and replacing $B_{\ell ,u}$ with $B_{\ell _s,u_s}$. The bounding box $B_{\ell _s,u_s}$ is obtained by solving the following 2n optimization problems

$$\begin{aligned} \begin{array}{rcl} \ell _s^i&{}&={}{\min }_{\ell \le x\le u,\ x\in {\mathcal {X}}} e_i'x \\ u_s^i&{}&={}{\max }_{\ell \le x\le u,\ x\in {\mathcal {X}}} e_i'x \end{array} \end{aligned}$$

(21)

where $e_i$ is the $i\hbox {th}$ column of the identity matrix, $i=1,\ldots ,n$. Note that Problem (21) is a linear programming (LP) problem in case of linear inequality constraints ${\mathcal {X}}=\{x\in {{\mathbb {R}}}^n\ Ax\le b\}$ . Then, we operate with new scaled variables ${\bar{x}}\in {{\mathbb {R}}}^n$, ${\bar{x}}_i\in [-1,1]$, and replace the original preference learning problem (2) with

$$\begin{aligned} \hbox {find}\ {\bar{x}}^\star \ \hbox {such that}\ \pi (x({\bar{x}}^\star ),x({\bar{x}}))\le 0,\ \forall {\bar{x}}\in {\mathcal {X}}_s,\ \ell _s\le x({\bar{x}})\le u_s \end{aligned}$$

where the scaling mapping $x:{{\mathbb {R}}}^n\rightarrow {{\mathbb {R}}}^n$ is defined as

$$\begin{aligned} x^j({\bar{x}})=\frac{u_s^j-\ell _s^j}{2}{\bar{x}}^j+\frac{u_s^j+\ell _s^j}{2},\ j=1,\ldots ,n \end{aligned}$$

where clearly $x^j(-1)=\ell _s$, $x^j(1)=u_s$, and ${\mathcal {X}}_s$ is the set

$$\begin{aligned} {\mathcal {X}}_s=\{{\bar{x}}\in {{\mathbb {R}}}^n:\ x({\bar{x}})\in {\mathcal {X}}\} \end{aligned}$$

(22)

When ${\mathcal {X}}$ is the polyhedron $\{x:\ Ax\le b\}$, (22) corresponds to defining the new polyhedron

$$\begin{aligned} {\mathcal {X}}_s=\{{\bar{x}}:\ {\bar{A}}{\bar{x}}\le {\bar{b}}\} \end{aligned}$$

where

$$\begin{aligned} \begin{array}{rcl} {\bar{A}}&={}A\mathrm{diag}\left( \frac{u_s-\ell _s}{2}\right) \\ {\bar{b}}&={}b-A\left( \frac{u_s+\ell _s}{2}\right) \end{array} \end{aligned}$$

and $\mathrm{diag}(\frac{u_s-\ell _s}{2})$ is the diagonal matrix whose diagonal elements are the components of $\frac{u_s-\ell _s}{2}.$

Note that in case the preference function $\pi$ is related to an underlying function f as in (3), applying scaling is equivalent to formulate the following scaled preference function

$$\begin{aligned} \pi ({\bar{x}}_1,{\bar{x}}_2)=\left\{ \begin{array}{ll} -1 &{}\hbox {if }f(x({\bar{x}}_1))<f(x({\bar{x}}_2))\\ 0 &{}\hbox {if }f(x({\bar{x}}_1))=f(x({\bar{x}}_2))\\ 1 &{}\hbox {if }f(x({\bar{x}}_1))>f(x({\bar{x}}_2)) \end{array}\right. \end{aligned}$$

5 Preference learning algorithm

Algorithm 1 summarizes the proposed approach to solve the optimization problem (2) by preferences using RBF interpolants (6) and the acquisition functions defined in Sect. 4.

In Step 3 Latin Hypercube Sampling (LHS) (McKay et al. 1979) is used to generate the initial set X of $N_{\mathrm{init}}$ samples. The generated samples may not satisfy the constraint $x\in {\mathcal {X}}$. We distinguish between two cases:

• i) the comparison $\pi (x_1,x_2)$ can be done even if $x_1\not \in {\mathcal {X}}$ and/or $x_2\not \in {\mathcal {X}}$;

• ii) $\pi (x_1,x_2)$ can only be evaluated if $x_1,x_2\in {\mathcal {X}}$.

In the first case, the initial comparisons are still useful to define the surrogate function. In the second case, a possible approach is to generate a number of samples larger than $N_{\mathrm{init}}$ and discard the samples $x_i\not \in {\mathcal {X}}$. An approach for performing this is suggested in Bemporad (2020, Algorithm 2).

Step 5.1.4 requires solving a global optimization problem. In this paper we use particle swarm optimization (PSO) (Kennedy 2010; Vaz and Vicente 2007) to solve problem (13). Alternative global optimization methods such as DIRECT (Jones 2009) or others methods (Huyer and Neumaier 1999; Rios and Sahinidis 2013) could be used to solve (13). Note that penalty functions can be used to take inequality constraints (1) into account, for example by replacing (13) with

$$\begin{aligned} x_{N+1}=\arg \min _{\ell \le x\le u} a(x)+\rho \varDelta {\hat{F}}\sum _{i=1}^q\max \{g_i(x),0\}^2 \end{aligned}$$

(23)

where $\rho \gg 1$ in (23).

Algorithm 1 consists of two phases: initialization and active learning. During initialization, sample $x_{N+1}$ is simply retrieved from the initial set $X=\{x_1,\ldots ,x_{N_{\mathrm{init}}}\}$. Instead, in the active learning phase, sample $x_{N+1}$ is obtained in Steps 5.1.1–5.1.4 by solving the optimization problem (13). Note that the construction of the acquisition function a is rather heuristic, therefore finding global solutions of very high accuracy of (13) is not required.

When using the RBF+IDW acquisition function (12), the exploration parameter $\delta$ promotes sampling the space in $[\ell ,u]\cap {\mathcal {X}}$ in areas that have not been explored yet. While setting $\delta \gg 1$ makes Algorithm 1 exploring the entire feasible region regardless of the results of the comparisons, setting $\delta =0$ can make Algorithm 1 rely only on the surrogate function ${\hat{f}}$ and miss the global optimizer. Note that using the RBF+PI acquisition function (20) does not require specifying the hyper-parameter $\delta$. On the other hand, the presence of the IDW function in the acquisition allows promoting an exploration which is independent of the surrogate, and therefore $\delta$ might be a useful tuning knob to have.

Figure 1 (upper plot) shows the samples generated by Algorithm 1 when applied to minimize the function f (9) in $[-3,3]$, by setting $\delta =1$, $N_{\mathrm{max}}=6$, $N_{\mathrm{init}}=3$, ${\mathcal {I}}_{\mathrm{sc}}=\emptyset$, $\varPsi$ generated by the inverse quadratic RBF with $\epsilon =2$, and $\sigma =\frac{1}{N_{\mathrm{max}}}$.

5.1 Computational complexity

Algorithm 1 solves $N_{\mathrm{max}}-N_{\mathrm{init}}$ quadratic or linear programs (8) with growing size, namely with $2N-1$ variables, a number q of linear inequality constraints with $N-1\le q\le 2(N-1)$ depending on the outcome of the preferences, and 2 equality constraints. Moreover, it solves $N_{\mathrm{max}}-N_{\mathrm{init}}$ global optimization problems (13) in the n-dimensional space, whose complexity depends on the used global optimizer. The computation of matrix $\varPsi$ requires overall $N_{\mathrm{max}}(N_{\mathrm{max}}-1)$ RBF values $\phi (\epsilon d(x_i,x_j))$, $i,j=1,\ldots ,N_{\mathrm{max}}$, $j\ne i$. The leave-one-out cross validation executed at Step 5.1.1 for recalibrating $\epsilon$ requires to formulate and solve problem (8) at most $N-1$ times. On top of the above analysis, one has to take account the cost of evaluating the preferences $\pi (x_{i(h)},x_{j(h)})$, $h=1,\ldots ,N_{\mathrm{max}}-1$.

6 Application to multi-objective optimization

The active preference learning methods introduced in the previous sections can be effectively used to solve multi-objective optimization problems of the form

$$\begin{aligned} \min _{\xi }&F(\xi )=\left[ \begin{array}{c} F_1(\xi )\\ \vdots \\ F_{n}(\xi ) \end{array}\right] \\ \mathrm{s.t.}&\,\,g(\xi )\le 0 \end{aligned}$$

where $\xi \in {{\mathbb {R}}}^{n_\xi }$ is the optimization vector, $F_i:{{\mathbb {R}}}^{n_\xi }\rightarrow {{\mathbb {R}}}$, $i=1,\ldots ,n$, are the objective functions, $n\ge 2$, and $g:{{\mathbb {R}}}^{n_\xi }\rightarrow {{\mathbb {R}}}^{n_g}$ is the function defining the constraints on $\xi$ (including possible box and linear constraints). In general Problem (25) admits infinitely many Pareto optimal solutions, leaving the selection of one of them a matter of preference.

Pareto optimal solutions can be expressed by scalarizing problem (25) into the following standard optimization problem

$$\begin{aligned} \xi ^\star (x)=\arg \min _\xi&\sum _{i=1}^{n}x_iF_i(\xi )\\ \mathrm{s.t.}&\,\,g(\xi )\le 0 \end{aligned}$$

where $x_1,\ldots ,x_{n}$ are nonnegative scalar weights. Let us model the preference between Pareto optimal solution through the preference function $\pi :{{\mathbb {R}}}^{n}\times {{\mathbb {R}}}^n\rightarrow \{-1,0,1\}$

$$\begin{aligned} \pi (x,y)=\left\{ \begin{array}{ll} -1 &{}\hbox {if }F(\xi ^\star (x))\hbox { is ``preferred to'' } F(\xi ^\star (y))\\ 0 &{}\hbox {if }F(\xi ^\star (x))\hbox { is ``as good as'' } F(\xi ^\star (y))\\ 1 &{}\hbox {if }F(\xi ^\star (y))\hbox { is ``preferred to'' } F(\xi ^\star (x)) \end{array}\right. \end{aligned}$$

(24)

where $x,y\in {{\mathbb {R}}}^n$. The optimal selection of a Pareto optimal solution can be therefore expressed as a preference optimization problem of the form (2), with $\ell =0$, $u=+\infty$, ${\mathcal {X}}={{\mathbb {R}}}^n$.

Without loss of generality, we can set $\sum _{i=1}^{n}x_i=1$ and eliminate $x_{n}=1-\sum _{i=1}^{n-1}x_i$, so to solve a preference optimization problem with $n-1$ variables under the constraints $x_i\ge 0$, $\sum _{i=1}^{n-1}x_i\le 1$. In Sect. 7.3 we will illustrate the effectiveness of the active preference learning algorithms introduced earlier in solving the multi-objective optimization problem (25) under an instance of the preference function (24).

7 Numerical results

In this section we test the active preference learning approach described in the previous sections on different optimization problems, only based on preference queries.

Computations are performed on an Intel i7-8550 CPU @1.8GHz machine in MATLAB R2019a. Both Algorithm 1 and the Bayesian active preference learning algorithm are run in interpreted code. Problem (13) (or (23), in case of constraints) is solved by the PSO solver (Vaz and Vicente 2009). For judging the quality of the solution obtained by active preference learning, the best between the solution obtained by running the optimization algorithm DIRECT (Jones 2009) through the NLopt interface (Johnson 2020) and by running the PSO solver (Vaz and Vicente 2009) was used as the reference global optimum, except for the brochu-6d benchmark example. In this case, both methods failed in finding the global minimum, so we used the GLIS algorithm (Bemporad 2020) to estimate it. The Latin hypercube sampling function lhsdesign of the Statistics and Machine Learning Toolbox of MATLAB is used to generate initial samples.

As our numerical experience is that the proposed algorithms are quite robust with respect to the values of the various hyper-parameters involved, we use the same hyper-parameters in all the considered examples, even if the functions that are minimized based on preferences are very different in terms of shape and number of variables.

7.1 Illustrative example

We first illustrate the behavior of Algorithm 1 when solving the following constrained benchmark global optimization problem proposed by Sasena et al. (2002):

$$\begin{aligned} \begin{array}{rl} \min &{} \displaystyle {2+\frac{1}{100}(x_2-x_1^2)^2+(1-x_1)^2+2(2-x_2)^2+7\sin \left( \frac{1}{2}x_1\right) \sin \left( \frac{7}{10}x_1x_2\right) } \\ \mathrm{s.t.}&{}\displaystyle {-\sin \left( x_1-x_2-\frac{\pi }{8}\right) \le 0}\\ &{}0\le x_1,x_2\le 5 \end{array} \end{aligned}$$

(25)

The minimizer of problem (25) is $x^\star =[2.7450\ 2.3523]'$ with optimal cost $f^\star =-1.1743$. Algorithm 1 is run with initial parameter $\epsilon =1$ and inverse quadratic RBF to fit the surrogate function, using the RBF+IDW acquisition criterion (12) with $\delta =1$, $N_{\mathrm{max}}=25$, $N_{\mathrm{init}}=8$ feasible initial samples, $\sigma =1$. Self-calibration is executed at steps N indexed by ${\mathcal {I}}_{\mathrm{{sc}}}=\{8,12,17,21\}$ over a grid of 10 values $\epsilon _\ell =\epsilon \theta _\ell$, $\theta _\ell \in \varTheta$, $\varTheta =\{10^{-1+\frac{1}{5}(\ell -1)}\}_{\ell =1}^{10}$.

Figure 3a shows the samples $X=\{x_1,\ldots ,x_{N_{\mathrm{max}}}\}$ generated by a run of Algorithm 1, Fig. 3b the best (unmeasured) value of the latent function f as a function of the number of preference queries, Fig. 4 the shapes of f and of the surrogate function ${\hat{f}}$. It is apparent that while ${\hat{f}}$ achieves the goal of driving the algorithm towards the global minimum, its shape is quite different from f, as it has been constructed only to honor the preference constraints (7) at sampled values. Therefore, given a new pair of samples $x_1$, $x_2$ that are located far away from the collected samples X, the surrogate function ${\hat{f}}$ may not be useful in predicting the outcome of the comparison $\pi (x_1,x_2)$.

It is apparent that ${\hat{f}}$ can be arbitrarily scaled and shifted without changing the outcome of preferences. While the arbitrariness in scaling is taken into account by the term $\varDelta {\hat{F}}$ in (12), it would be immediate to modify problem (8) to include the equality constraint

$$\begin{aligned} \sum _{j=1}^N \phi (\epsilon d(x_{i^\star },x_{j}))\beta _j=0 \end{aligned}$$

so that by construction ${\hat{f}}$ is zero at the current best sample $x_{i^\star }$.

Fig. 3

Preference-based global optimization of Sasena benchmark function

Fig. 4

Latent function f and surrogate ${\hat{f}}$ from the problem defined in (25), along with the samples X (red circles) generated by Algorithm 1 (Color figure online)

7.2 Benchmark global optimization problems

We test the proposed global optimization algorithm on standard benchmark global optimization problems. Problems brochu-2d, brochu-4d, brochu-6d were proposed in Brochu et al. (2008) and are defined as follows:

$$\begin{aligned} \begin{array}{rcl} f_d(x)&{}&= \displaystyle {\sum _{i=1}^d\sin (x_i)+\frac{1}{3}x_i+\sin (12 x_i)}\\ f_{\textsf {brochu-2d}}(x)&{}&= -\max \{f_2(x)-1,0\}\\ f_{\textsf {brochu-4d}}(x)&{}&= -f_4(x)\\ f_{\textsf {brochu-6d}}(x)&{}&= -f_6(x) \end{array} \end{aligned}$$

with $x\in [0,1]^d$, where the minus sign is introduced as we minimize the latent function, while in Brochu et al. (2008) it is maximized. For the definition of the remaining benchmark functions and associated bounds on variables the reader is referred to Bemporad (2020); Jamil and Yang (2013).

In all tests, the inverse quadratic RBF with initial parameter $\epsilon =1$ is used in Algorithm 1, with $\delta =2$ in (12), $N_{\mathrm{init}}=\lceil \frac{N_{\mathrm{max}}}{3} \rceil$ initial feasible samples generated by Latin Hypercube Sampling as described in Bemporad (2020, Algorithm 2), and $\sigma =\frac{1}{N_{\mathrm{max}}}$. Self-calibration is executed at steps N indexed by ${\mathcal {I}}_{\mathrm{{sc}}}=\{N_{\mathrm{init}},N_{\mathrm{init}}+\lceil \frac{N_{\mathrm{max}}-N_{rm init}}{4}\rceil , N_{\mathrm{init}}+\lceil \frac{N_{\mathrm{max}}-N_{\mathrm{init}}}{2}\rceil ,N_{\mathrm{init}}+\lceil \frac{3(N_{\mathrm{max}}-N_{\mathrm{init}})}{4}\rceil \}$ over a grid of 10 values $\epsilon _\ell =\epsilon \theta _\ell$, $\theta _\ell \in \varTheta$, $\ell =1,\ldots ,10$, with the same set $\varTheta$ used to solve problem (25).

For comparison, the benchmark problems are also solved by the Bayesian active preference learning algorithm described in Brochu et al. (2008), which is based on a Gaussian Process (GP) approximation of the posterior distribution of the latent preference function f. The posterior GP is computed by considering a zero-mean Gaussian process prior, where the prior covariance between the values of the latent function at the two different inputs $x \in {\mathbb {R}}^n$ and $y \in {\mathbb {R}}^n$ is defined by the squared exponential kernel

$$\begin{aligned} {\mathcal {K}}(x,y) = \sigma _f^2 e^{\frac{ \left\| x-y\right\| ^2 }{2\sigma _l^2}} \end{aligned}$$

where $\sigma _f$ and $\sigma _l$ are positive hyper-parameters. The likelihood describing the observed preferences is constructed by considering the following probabilistic description of the preference $\pi (x,y)$:

$$\begin{aligned} \Pr (\pi (x,y)|f(x), f(y)) = \left\{ \begin{array}{ll} Q\left( \frac{f(y)-f(x)}{\sqrt{2} \sigma _e}\right) &{} \hbox {if}\ \pi (x,y)=-1 \\ Q\left( \frac{f(x)-f(y)}{\sqrt{2} \sigma _e}\right) &{} \hbox {if}\ \pi (x,y)=1 \end{array} \right. \end{aligned}$$

where Q is the cumulative distribution of the standard Normal distribution, and $\sigma _e$ is the standard deviation of a zero-mean Gaussian noise which is introduced as a contamination term on the latent function f in order to allow some tolerance on the preference relations (see (Chu and Ghahramani 2005b) for details). The preference relation $\pi (x,y)=0$ is treated as two independent observations with preferences $\pi (x,y)=-1$ and $\pi (x,y)=1$. The hyper-parameters $\sigma _f$ and $\sigma _l$, as well as the noise standard deviation $\sigma _e$, are computed by maximizing the probability of the evidence (Chu and Ghahramani 2005b, Section 2.2). For a fair comparison with the RBF-based algorithm in this paper, these hyper-parameters are re-computed at the steps indexed by ${\mathcal {I}}_{\mathrm{{sc}}}$. Furthermore, the same number $N_{\mathrm{init}}$ of initial feasible samples is generated using Latin hypercube sampling (McKay et al. 1979).

Algorithm 1 is executed using both the acquisition function (12) (RBF+IDW) and (20) (RBF+PI), and results compared against those obtained by Bayesian active preference learning (PBO), using the expected improvement as an acquisition function (Brochu et al. 2008, Sec. 2.3). Results are plotted in Figs. 5 and 6, where the median performance and the band defined by the best- and worst-case instances over $N_{\mathrm{test}}=20$ runs is reported as a function of the number of queried preferences. The vertical line represents the last query $N_{\mathrm{init}}-1$ at which active preference learning begins. The dashed red line in the figures shows the global minimum.

Fig. 5

Comparison between Algorithm 1 based on IDW acquisition (12) (RBF+IDW) and Bayesian preference learning (PBO) on benchmark problems: median (thick line) and best/worst-case band over $N_{\mathrm{test}}=20$ tests of the best value found of the latent function. The dashed red line corresponds to the global optimum. The thin green line shows the median obtained by RBF+PI, as reported in Fig. 6 (Color figure online)

Fig. 6

Comparison between Algorithm 1 based on probability of improvement (20) (RBF+PI) and Bayesian preference learning (PBO) on benchmark problems: median (thick line) and best/worst-case band over $N_{\mathrm{test}}=20$ tests of the best value found of the latent function. The dashed red line corresponds to the global optimum. The thin purple line shows the median obtained by RBF+IDW, as reported in Fig. 5 (Color figure online)

The results of Figs. 5 and 6 clearly show that, in all the considered benchmarks, the RBF+IDW and RBF+PI algorithms perform as good as (and often outperform) PBO in approaching the minimum of the latent function. Furthermore, the RBF+IDW and RBF+PI methods are computationally lighter than PBO, as shown in Table 1, where the average CPU time spent on solving each benchmark problem is reported¹. The RBF+IDW and RBF+PI algorithms have similar performance and computational load.

Table 1 CPU time (s) spent for solving each benchmark problem considered in the comparison, averaged over $N_{\mathrm{test}}=20$ runs

7.3 Multi-objective optimization by preferences

We consider the following multi-objective optimization problem

$$\begin{aligned} \min _\xi&\,F(\xi )=\left[ \begin{array}{c} (2\xi _1\sin \xi _2-3\cos (\xi _1\xi _2))^2\\ \xi _3^2(\xi _1+\xi _2)^4\\ (\xi _1+\xi _2+\xi _3)^2 \end{array}\right] \\ \mathrm{s.t.}&-1\le \xi _i\le 1,\ i=1,2,3 \end{aligned}$$

Let assume that the preference in  (24) is expressed by a decision maker in terms of “similarity” of the achieved optimal objectives, that is a Pareto optimal solution is “preferred to” another one if the objectives $F_1,F_2,F_3$ evaluated at $\xi ^\star (x)$ are closer to each other. In our numerical tests we therefore mimic the decision maker by defining a synthetic preference function $\pi$ as in (3) via the following latent function $f:{{\mathbb {R}}}^n\rightarrow {{\mathbb {R}}}$

$$\begin{aligned} f(x)=\left\| \left[ \begin{array}{c} F(\xi ^\star (x))-F_2(\xi ^\star (x))\\ F_1(\xi ^\star (x))-F_3(\xi ^\star (x))\\ F_2(\xi ^\star (x))-F_3(\xi ^\star (x)) \end{array}\right] \right\| \end{aligned}$$

(26)

As we have three objectives, we only optimize over $x_1,x_2$ and set $x_3=1-x_1-x_2$, under the constraints $x_1,x_2\ge 0$, $x_1+x_2\le 1$.

Figure 7 shows the results obtained by running $N_{\mathrm{test}}=20$ times Algorithm 1 with $\epsilon =1$ and the same other settings as in the benchmarks examples described in Sect. 7.2. Figure 7a shows the results when when the IDW exploration term is used in (12) with $\delta =2$, Fig. 7b when the PI acquisition function (20) is used.

The optimal scalarization coefficients returned by the algorithm are $x^\star _1=0.2857$, $x_2^\star =0.1952$ and $x_3^\star =1-x_1^\star -x_2^\star =0.5190$, that lead to $F^\star =F(\xi ^\star (x^\star ))=[1.3921\ 1.3978\ 1.3895]'$. The latent function (26) optimized by the algorithm is plotted in Fig. 8. Note that the optimal multi-objective F achieved by setting $x_1=x_2=x_3=\frac{1}{3}$, corresponding to the intuitive assignment of equal scalarization coefficients, leads to the much worse result $F(\xi ^\star ([\frac{1}{3}\ \frac{1}{3}\ \frac{1}{3}]'))=[0.2221\ 0.2581\ 2.9026]'$.

Fig. 7

Multi-objective optimization example: median (thick line) and best/worst-case band over $N_{\mathrm{test}}=20$ tests of latent function (26) as a function of queried preferences

Fig. 8

Multi-objective optimization example: latent function (26)

7.4 Choosing optimal cost-sensitive classifiers via preferences

We apply now the active preference learning algorithm to solve the problem of choosing optimal classifiers for object recognition from images when different costs are associated to different types of misclassification errors.

A four-class convolutional neural network (CNN) classifier with 3 hidden layers and a soft-max output layer is trained using 20000 samples, which consist of all and only the images of the CIFAR-10 dataset (Krizhevsky 2009) labelled as: automobile, deer, frog, ship, that are referred in the following as classes ${\mathcal {C}}_1$, ${\mathcal {C}}_2$, ${\mathcal {C}}_3$, ${\mathcal {C}}_4$, respectively. The network is trained in 150 epochs using the Adam algorithm (Kingma and Ba 2015) and batches of size 2000, achieving an accuracy of 81% over a validation dataset of 4000 samples.

We assume that a decision maker associates different costs to misclassified objects and the predicted class of an image ${\mathcal {U}}$ is computed as

$$\begin{aligned} \hat{{\mathcal {C}}} = \arg \max _{i = \{1,2,3,4\}} x_ip({\mathcal {C}}_i|{\mathcal {U}}) \end{aligned}$$

(27)

where $p({\mathcal {C}}_i|{\mathcal {U}})$ is the network’s confidence (namely, the output of the softmax layer) that the image ${\mathcal {U}}$ is in class ${\mathcal {C}}_i$, and $x_i$ are nonnegative weights to be tuned in order to take into account the preferences of the decision maker. As for the multi-objective optimization example of Sect. 7.3, without loss of generality we set $\sum _{i=1}^{4}x_i=1$ and the constraints $x_i\ge 0$, $\sum _{i=1}^{3}x_i\le 1$, thus eliminating the variable $x_{4}=1-\sum _{i=1}^{3}x_i$.

In our numerical tests we mimic the preferences expressed by the decision maker by defining the synthetic preference function $\pi$ as in (3), where the (unknown) latent function $f:{{\mathbb {R}}}^n\rightarrow {{\mathbb {R}}}$ is defined as

$$\begin{aligned} f(x,m)= \left( 1+m\right) \sum _{i=1}^4 \sum _{i=1}^4 C(i,j)r(i,j,x) \end{aligned}$$

(28)

In (28), the term r(i, j, x) is the number of samples in the validation set of actual class ${\mathcal {C}}_i$ that are predicted as class ${\mathcal {C}}_j$ according to the decision rule (27), while C(i, j) is the cost of misclassifying a sample of actual class ${\mathcal {C}}_i$ as class ${\mathcal {C}}_j$. The considered costs are reported in Table 2, which describes the behaviour of the decision maker in associating a higher cost in misclassifying automobile and ship rather than misclassifying deer and frog. In (28), m is a random variable uniformly distributed between $-0.15$ and 0.15 and it is introduced to represent a possible inconsistency in the preferences made by the user.

Figure 9 shows the results obtained by running $N_{\mathrm{test}}=30$ times Algorithm 1, $\epsilon =1$, $N_{\mathrm{init}}=10$, $\delta =2$ for RBF+IDW, and the same other settings as in the benchmarks examples described in Sect. 7.2, and by running preference-based Bayesian optimization ($\delta =2$ is used for RBF+IDW). The optimal weights returned by the algorithm after evaluating $N_{\mathrm{max}}=40$ samples are $x^\star _1=0.3267$, $x_2^\star =0.1613$, $x_3^\star =0.1944$ and $x_4^\star =1-x_1^\star -x_2^\star -x_3^\star =0.3176$, that lead to a noise-free cost $f(x^\star ,0)$ in (28) equal to 2244 (against $f(x,0)= 2585$ obtained for unweighted costs, namely, for $x_1=x_2=x_3=x_4=0.25$). As expected, higher weights are associated to automobile and ship (class ${\mathcal {C}}_1$ and ${\mathcal {C}}_4$, respectively). For judging the quality of the computed solution, the minimum of the noise-free cost $f(x^\star ,0)=2201$ is computed by PSO and used as the reference global optimum.

The obtained results show comparable performance among RBF+IDW, RBF+PI and PBO, with the median of the three methods converging to a similar value after 40 iterations. Because of the random term m influencing the underlying preference function f(x, m), the minimum of the noise-free cost $f(x^\star ,0)=2201$ is never achieved (dashed red line in Fig. 9). Nevertheless, it is interesting to notice that the worst solution obtained by RBF+IDW is even better than the noise-free unweighted cost $f(x,0)= 2585$.

We remark that the purpose of this example is only to illustrate the effectiveness of the proposed preference-based learning algorithms, rather than to propose a new good way of solving the classification problem itself.

Fig. 9

Noise-free cost f(x, 0) as a function of the number of queried preferences. Median (solid lines) and bands defined by the best- and worst-case instances over $N_{\mathrm{test}}=30$; reference global optimum achieved by PSO (dashed red line) (Color figure online)

Table 2 Cost matrix

7.5 Dependence of RBF+IDW on the acquisition parameter $\delta$

To analyze the influence of $\delta$ in defining the RBF+IDW acquisition function (12), we consider the behavior of Algorithm 1 for varying values of $\delta$ when solving the ackley benchmark problem. Each experiment is repeated $N_{\mathrm{test}}=20$ times. The distribution of the best achieved function value obtained after generating $N=20, 30, 70, 100$ samples is reported in Fig. 10. The figure also shows the distribution of the best function values obtained by just randomly sampling the feasible set.

Note that in the absence of the exploration term z(x) in the RBF+IDW acquisition function (12), that is for $\delta =0$, the algorithm easily gets trapped away from the global minimum. For comparison, in Fig. 10 we also report the behavior obtained by merely sampling the set of feasible vectors randomly by LHS (labelled as rand in the plot), which clearly shows the benefits brought by the proposed method.

Fig. 10

Distribution over $N_{\mathrm{test}}=20$ tests of the best achieved function value of ackley function after N queries obtained by running Algorithm 1 with RBF+IDW acquisition (12) for different values of $\delta$. The case of pure minimization of the surrogate function without exploration term corresponds to $\delta =0$. The results obtained by sampling the set of feasibly vectors randomly are labeled as rand

8 Conclusions

In this paper we have proposed an algorithm for choosing the vector of decision variables that is best in accordance with pairwise comparisons with all possible other values. Based on the outcome of an incremental number of comparisons between given samples of the decision vector, the main idea is to attempt learning a latent cost function, using radial basis function interpolation, that, when compared at such samples, provides the same preference outcomes. The algorithm actively learns such a surrogate function by proposing iteratively a new sample to compare based on a trade-off between minimizing the surrogate and visiting areas of the decision space that have not yet been explored. Through several numerical tests, we have shown that the algorithm usually performs better than active preference learning based on Bayesian optimization, in that it frequently approaches the optimal decision vector with less computations. We have proposed two different criteria (IDW, PI) to drive the exploration of the space of decision vectors. According to our experience there is not a clear winner between the two criteria, so both alternatives should be considered.

The approach can be extended in several directions. First, rather than only comparing the new sample $x_{N+1}$ with the current best $x^\star$, one could ask for expressing preferences also with one or more of the other existing samples $x_1,\ldots ,x_N$. Second, we could expand the codomain of the comparison function $\pi (x,y)$ to say $\{-2,-1,0,1,2\}$ where $\pi (x,y)=\pm 2$ means “x is much better/much worse than y”, and consequently extend (7) to include a much larger separation than $\sigma$ whenever the corresponding preference $\pi =\pm 2$. Third, often one can qualitatively assess whether a given sample x is “very good”, “good”, “neutral”, “bad”, or “very bad”, independently of how it compares to other values, and take this additional information into account when learning the surrogate function, for example by including additional constraints that force the surrogate function to lie in [0, 0.2] on all “very bad” samples, in [0.2, 0.4] on all “bad” samples, ..., in [0.8, 1] on all “very good” ones, and choosing an appropriate value of $\sigma$. Furthermore, while a certain tolerance to errors in assessing preferences is built-in in the algorithm thanks to the use of slack variables in (7), the approach could be extended to better take evaluation errors into account in the overall formulation and solution method.

Regarding the constraints (1) imposed in the preference-based optimization problem, we have assumed that, contrarily to the objective function f, they are known. An interesting subject for future research is the case when the constraint function g is also unknown. The algorithm proposed in this paper already handles such a case indirectly, in that the samples that according to the human oracle violate the constraints will never be labeled as “preferred” when compared to feasible samples. Accordingly, we can interpret this as the fact that our algorithm would learn a function that is a surrogate of the latent objective function augmented by a penalty function on constraint violation. In alternative, one may explicitly train a binary classifier, based on human assessment of whether a generated sample $x_k$ is feasible or not, and take the output of the classifier into account in the acquisition function.

Finally, we remark that one should be careful in using the learned surrogate function to extrapolate preferences on arbitrary new pairs of decision vectors, as the learning process is tailored to detecting the optimizer rather than globally approximating the unknown latent function, and moreover the chosen RBFs may not be adequate enough for reproducing the shape of the unknown latent function.

Appendix

1.1 Proof of Theorem 1

Let $\beta (\lambda )$ be the minimizer of problem (14) for some positive scalar $\lambda$. Let us define $\tau (\lambda )=\left\| \beta (\lambda ) \right\|$ and the set $B_{\tau } = \{\beta \in {\mathbb {R}}^N: \Vert \beta \Vert =\tau (\lambda ) \}$. Then, we have

$$\begin{aligned} \beta (\lambda ) &=\arg \min _{\beta \in {\mathbb {R}}^N} \sum _{h=1}^{M} c_{h} \ell _{b_{h}}(\varPhi (\epsilon ,X, x_{i(h)}, x_{j(h)})'\beta ) + \frac{\lambda }{2} \left\| \beta \right\| ^2 \\ &=\arg \min _{\beta \in B_{\tau }} \sum _{h=1}^{M} c_{h} \ell _{b_{h}}(\varPhi (\epsilon ,X, x_{i(h)}, x_{j(h)})'\beta ) \\ &=\tau (\lambda )\arg \min _{u: \Vert u\Vert =1} \sum _{h=1}^{M} c_{h} \ell _{b_{h}}(\tau (\lambda )\varPhi (\epsilon ,X, x_{i(h)}, x_{j(h)})'u) \\ &=\tau (\lambda ) u^\star \end{aligned}$$

where $u^\star$ is the minimizer of (16). Thus, $u^\star =\frac{\beta (\lambda )}{\tau (\lambda )}$.

1.2 Proof of Theorem 2

Let $u, {\bar{u}} \in {\mathbb {R}}^N$ be arbitrary unit vectors. Then, there exists an orthogonal (rotation) matrix R with determinant $+1$ such that ${\bar{u}} = R'u$. Let $\varphi : {\mathbb {R}}^N \rightarrow {\mathbb {R}}^N$ be a vector value function defined as $\varphi (v)=Rv$. Note that the Jacobian matrix $J_{\varphi }$ of $\varphi$ is R, and thus its determinant $det(J_{\varphi })$ is equal to $+1$.

Let us now write the integral $I_t({\bar{c}}_t,\tau ,u)$ in (18) as

$$\begin{aligned} I_t({\bar{c}}_t,\tau ,u) &=\int _{ \varPhi \in {\mathbb {R}}^N} e^{-{\bar{c}}_{t}\ell _{t}(\tau \varPhi 'u)}\kappa (\varPhi ) d\varPhi \\ &=\int _{ v \in {\mathbb {R}}^N} e^{-{\bar{c}}_{t}\ell _{t}(\tau \varphi (v)'u)} \kappa (\varphi (v)) det(J_{\varphi }) dv \\ &=\int _{ v \in {\mathbb {R}}^N} e^{-{\bar{c}}_{t}\ell _{t}(\tau v'R'u)} \kappa (v) dv \\ &=\int _{ v \in {\mathbb {R}}^N} e^{-{\bar{c}}_{t}\ell _{t}(\tau v'{\bar{u}})} \kappa (v) dv \\ &=I_t({\bar{c}}_t,\tau ,{\bar{u}}) \end{aligned}$$

where the third equality holds since $\kappa (\varphi (v))=e^{-\varphi (v)'\varphi (v)}=e^{-v'RR'v}=e^{-v'v} = \kappa (v)$.