A dynamic ensemble approach to robust classification in the presence of missing data

Abstract

Many real-world datasets suffer from missing or incomplete data. In the healthcare setting, for example, certain patient measurement parameters, such as vitals and/or lab values, may be missing due to insufficient monitoring. When present, however, these features could be highly discriminative in predicting aspects of patient state. Therefore, it is desirable to incorporate these sparsely measured features into a predictive model. Training predictive algorithms on such datasets is complicated by the missing data. Overcoming this problem is usually achieved by first estimating values for the missing data, which is referred to as data imputation. Without strong prior knowledge about the relationship between features though, it is common to fill in missing values with their respective population mean or median. The accuracy of this approach is limited, however, and may simply inject noise into the data. We propose a two-stage machine learning algorithm that learns a dynamic classifier ensemble from an incomplete dataset without data imputation. The algorithm is very simple to implement and applicable across a wide range of problems. Our method first employs a variant of AdaBoost to learn a set of low-dimensional classifiers, each of which abstains from predicting if its dependent feature(s) are missing. Our novel contribution is the secondary dynamic ensemble learning stage in which the low-dimensional classifiers are combined using a dynamic weighting that depends on the pattern of measured features in the present input data. This allows the model to be resilient to missing data by adjusting the strength of certain classifiers to account for missing features. We apply our algorithm to early detection of hemodynamic instability in ICU patients. Providing an effective risk score of hemodynamic instability has the potential to give the clinician sufficient time to intervene, thereby reducing the chance of organ damage due to insufficient blood perfusion. We compare the results of our algorithm to other common missing data approaches, including mean imputation and multiple imputation methods, and discuss the advantages of the approach given the constraints of the application domain (e.g., high specificity to combat hospital alarm fatigue).

1 Introduction

The fundamental purpose of the cardiovascular system is to ensure adequate perfusion and oxygenation of body tissue to maintain normal, healthy tissue and organ function. A healthy physiological system has a number of compensatory mechanisms in place that help to maintain an appropriate blood pressure and cardiac output to enable sufficient perfusion of the end organs. Patients in the intensive care unit (ICU), however, are often physiologically compromised so that insults from significant disease processes such as sepsis, hemorrhage, and acute heart failure may result in significant impairment of these control functions, resulting in hemodynamic deterioration. Thus, in such cases, the ICU clinician is often challenged to optimize hemodynamics by assimilating the myriad ICU data and reacting with appropriate interventions in the form of intravenous fluids, blood products, and pharmacological agents, to help the patient maintain adequate cardiac output and perfusion. The early detection of hemodynamic instability episodes and the immediate initiation of appropriate corrective intervention can significantly improve patient outcome.

ICU clinicians are presented with a large number of physiological data consisting of periodic and frequently sampled measurements (e.g. second-by-second, minute-by-minute, 5, or 15-min, depending on the particular device configuration), such as heart rate and respiratory rate, as well as aperiodic measurements, such as noninvasive blood pressure and laboratory studies. Labs are only measured every few hours or once a day to avoid unnecessary blood draws. Moreover, certain lab results may only be ordered if a patient is suspected of a certain condition. Lactate, for example, may only be measured for 15–20 % of ICU patients that are suspected of having lactic acidosis. The interpretation and reaction of these rich data sources to impending hemodynamic instability can be a particularly difficult task in the presence of overwhelming volumes of data, frequent false alarms, and frequently interrupted workflows.

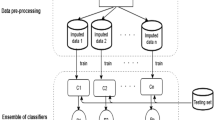
We propose a machine learning algorithm to detect hemodynamic deterioration in its early stages, enabling clinicians to direct attention to those patients who may benefit from it most, by creating an algorithm that meaningfully combines data that is available in the current ICU environment. This includes information that may not be commonly measured, but when measured can be very important. Our algorithm trains a predictive classifier that is robust to missing data and handles missing data without data imputation. Avoiding data imputation makes the algorithm very simple and efficient for real-time production scenarios. Instead, the algorithm learns a dynamic ensemble comprising many univariate or low-dimensional classifiers, each of which abstains from predicting if its dependent feature(s) are missing. This is achieved by a two-stage learning algorithm: first, a variant of AdaBoost learns a set of low-dimensional classifiers, each of which abstains from predicting if its dependent feature(s) are missing. Our novel contribution is the secondary dynamic ensemble learning stage in which the low-dimensional classifiers are combined using a dynamic weighting that depends on the pattern of measured features in the present input data. This allows the model to be resilient to missing data by adjusting the strength of certain classifiers to account for missing features.

2 Data

Patient data were obtained from the eResearch Institute (McShea et al. 2010); the data included records from 105,000 patients cared for at 50 hospitals. We refined the dataset to include only those hospitals that reported fluids administered at least hourly so that we could better gauge each patient’s therapy. From these hospitals, we excluded patients who were designated as “Do Not Resuscitate” (DNR), “Comfort Measures Only” (CMO), or “Allow Natural Death” (AND). This resulted in a finalized dataset of 40,883 patients from across 25 hospitals, ranging from large teaching hospitals to smaller, community hospitals, with a hospital mortality ranging from 0 to 7.8 % (median = 3 %).

The dataset originated from a non-annotated database, and as such, no gold standard marker of hemodynamic instability was available. Instead, certain interventions by clinicians were used to demarcate episodes of hemodynamic instability. The criteria for instability, highlighted in Table 1, were developed based on a strong consensus among a group of experienced intensive care physicians.¹

Table 1 Description of intervention criteria used to label patient ICU segments as hemodynamically unstable

For purposes of training and validation, the patients ICU stays were divided into 6 h segments, and these segments were labeled as either stable or unstable. Unstable segments were the 6 h period prior to any intervention listed in Table 1. Patients could have multiple interventions, and thus multiple intervention segments. However, for subsequent interventions there must be a stable period of 18 h without an intervention. Stable segments were chosen from patients who had none of the interventions listed in Table 1 or who ended their ICU stay with at least 18 h without an intervention. A 6 h segment was chosen at random from these stable periods for the stable segments.

The above criteria resulted in 49,256 labeled segments (44,019 stable; 5237 unstable: instability prevalence 10.6 %). We extracted a total of 57 features that comprised vital signs, lab values, and demographic information about the patient. These features, along with their measurement availability, are categorized by panel and component tests (Frassica 2005) in Table 2. For each segment, the data extracted 1 h prior to intervention was used for training. We used sample-and-hold imputation to fill in features that were not available 1 h prior to intervention, but were measured sometime within a 6 h period prior. Even despite this imputation technique, many of the features were still missing a large number of values.

Table 2 Listing of features used for hemodynamic instability prediction, along with their measurement frequency (percentage of segments)

3 Methods

In the following, vectors will be denoted by bold-face: $\varvec{x}$. To reference the jth element of $\varvec{x}$, we use the notation $x_j$.

We are given a dataset of n labeled samples $(\varvec{x^{(1)}},y^{(1)}),\ldots ,(\varvec{x^{(n)}},y^{(n)})$, where each $\varvec{x^{(i)}}\in \mathbb {R}^p$ is a p-dimensional feature vector and $y^{(i)}\in \{-1,+1\}$ is its associated categorical label that we wish to predict. In the case of the hemodynamic instability dataset from Sect. 2, each element of $\varvec{x}$ corresponds to a feature listed in Table 2, and y is the patient state label (either “stable” or “unstable”). We assume the dataset is incomplete in that features are not present or measured in every feature pattern. Certain features, such as Lactate and Central Venous Pressure, may be missing on 80 % or more of samples. We denote the jth feature being missing on the $i^{th}$ sample as $x^{(i)}_j=\phi$.

As discussed in the Introduction, our approach can be broken down into two stages. In Sect. 3.1, we discuss using a variant of AdaBoost to learn the set of low-dimensional classifiers, each of which abstains when its dependent feature(s) are missing. This abstaining AdaBoost model was first introduced by Schapire and Singer (1999) and applied to missing data applications in Smeraldi et al. (2010). Then in Sect. 3.2, we introduce the second stage of the algorithm that learns a dynamic ensemble, which weights the various classifiers based on the presence/absence pattern of the input features.

3.1 AdaBoost with abstaining

AdaBoost (Schapire and Singer 1999) is a very effective machine learning technique for building a powerful classifier from an ensemble of “weak learners”. Specifically, the boosted classifier $H(\varvec{x})$ is modeled as a generalized additive model of many base hypotheses:

$$\begin{aligned} H(\varvec{x}) = b + \sum _{t} \alpha _t h(\varvec{x}; \varvec{\theta _t}) \end{aligned}$$

(1)

where b is a constant bias that accounts for the prevalence of the categories, and each $h(\varvec{x};\varvec{\theta _t})$ is a function of $\varvec{x}$, with parameters given by the elements in the vector $\varvec{\theta _t}$, and produces a classification output (+1 or $-1$). We also allow each of the base classifiers to abstain from voting (output = 0). A final classification decision is assigned by taking the sign of $H(\varvec{x})$, which results in a weighted majority vote over the base classifiers in the model.

As is common for AdaBoost applications, we use the class of 1-dimensional decision stumps as the base hypotheses:

$$\begin{aligned} h(\varvec{x}; \varvec{\theta _t}=(j,\tau )) = \left\{ \begin{array}{rl} +1\text {, } &{} x_j \ge \tau \\ -1\text {, } &{} x_j < \tau \\ 0\text {, } &{} x_j = \phi \\ \end{array}\right. \end{aligned}$$

(2)

Thus, each base classifier votes by comparing one of the p features in the data to a threshold. If that particular feature is missing, the base classifier abstains from voting.

The algorithm to learn the bias b, base hypotheses $h(\varvec{x};\varvec{\theta _t})$ and weightings $\alpha _t$ is a version of the traditional discrete AdaBoost algorithm adapted to accommodate classifiers that abstain, which was described in Schapire and Singer (1999). This algorithm has been employed previously for missing data problems in predicting protein-protein interactions (Smeraldi et al. 2010), but since it is a non-standard application of AdaBoost, we briefly reproduce the details of the algorithm here.

AdaBoost seeks to minimize the exponential loss function:

$$\begin{aligned} \sum _{i=1}^n \exp \left( -y^{(i)} H(\varvec{x^{(i)}})\right) \end{aligned}$$

(3)

which can be shown to be an upper bound on the training error (Freund and Schapire 1999). Optimization proceeds in a greedy fashion: at each iteration (or boosting round) t, a new classifier is added to the model that most decreases the objective function in (3). Thus, at iteration $t=T$, we fix the base classifiers learned at iterations $1,\dots ,T-1$ and add a new classifier $h(\varvec{x}; \varvec{\theta _T})$, weighted by $\alpha _T$, that minimizes the exponential loss objective:

$$\begin{aligned}&\sum _{i=1}^n \exp \left( -y^{(i)}\left[ b + \sum _{t=1}^{T-1} \alpha _t h(\varvec{x^{(i)}}; \varvec{\theta _t}) + \alpha _{T} h(\varvec{x^{(i)}}; \varvec{\theta _T})\right] \right) \end{aligned}$$

(4)

$$\begin{aligned}&\quad = \sum _{i=1}^n w_i^{(T)} \exp \left( -y^{(i)} \alpha _T h(\varvec{x^{(i)}}; \varvec{\theta _T})\right) \end{aligned}$$

(5)

where $w_1^{(T)},w_2^{(T)},\ldots ,w_n^{(T)}$ is the current weight distribution on the training data:

$$\begin{aligned} w_i^{(T)} = \exp \left( -y^{(i)}\left[ b + \sum _{t=1}^{T-1} \alpha _t h(\varvec{x^{(i)}}; \varvec{\theta _t})\right] \right) \end{aligned}$$

(6)

These weights reflect how well the current classifier (up to iteration $T-1$) is performing on each of the training examples: the larger the weight, the poorer the classifier predicts the true label of that example.

The algorithm boils down to selecting $h(\varvec{x^{(i)}}; \varvec{\theta _T})$ and $\alpha _T$. It can be shown (Schapire and Singer 1999) that the classifier that most decreases the objective is the one that minimizes:

$$\begin{aligned}&D_0(\varvec{\theta _T}) + 2\sqrt{D_{+}(\varvec{\theta _T})D_{-}(\varvec{\theta _T})} \end{aligned}$$

(7)

$$\begin{aligned}&\text {where} \qquad D_0(\varvec{\theta _T}) = \sum _{i=1}^n w_i^{(T)} \mathbb {I}(h(\varvec{x^{(i)}};\varvec{\theta _T}) = 0) \end{aligned}$$

(8)

$$\begin{aligned}&D_{+}(\varvec{\theta _T}) = \sum _{i=1}^n w_i^{(T)} \mathbb {I}(y^{(i)}h(\varvec{x^{(i)}};\varvec{\theta _T}) > 0) \end{aligned}$$

(9)

$$\begin{aligned}&D_{-}(\varvec{\theta _T}) = \sum _{i=1}^n w_i^{(T)} \mathbb {I}(y^{(i)}h(\varvec{x^{(i)}};\varvec{\theta _T}) < 0) \end{aligned}$$

(10)

where $\mathbb {I}(x)$ is the indicator function. Intuitively, $D_0(\varvec{\theta _T})$, $D_{+}(\varvec{\theta _T})$ and $D_{-}(\varvec{\theta _T})$ are the fraction of examples (under the current training weight distribution) for which the classifier abstains, classifies correctly, and classifies incorrectly. This best classifier can be identified efficiently from the class of decision stumps.

Once the classifier has been selected, the weight can be computed analytically by setting the derivative of (5) to zero, resulting in the following update:

$$\begin{aligned} \alpha _T = \frac{1}{2} \log \left( \frac{D_{+}(\varvec{\theta _T})}{D_{-}(\varvec{\theta _T})}\right) \end{aligned}$$

(11)

Notice that even though the classifier selection criterion (7) penalizes a classifier for abstaining, the weighting $\alpha _T$ that it is assigned if it is selected is not affected. Instead, a classifier’s weighting only depends on how discriminative it is when it votes, and is not penalized for abstaining.

Upon incorporating the weighted classifier $\alpha _Th(\varvec{x};\varvec{\theta _T})$, we update the weight distribution:

$$\begin{aligned} w_i^{(T+1)} \leftarrow w_i^{(T)} \exp \left( -y^{(i)} \alpha _T h(\varvec{x^{(i)}};\varvec{\theta _T})\right) \end{aligned}$$

(12)

and proceed to the next round of boosting $t=T+1$.

Since the prevalence of hemodynamic instability in the ICU dataset is highly unbalanced (roughly 10:1), the best classifier to add may often be one that is highly biased towards the most prevalent category. To remove this effect, we re-tune the bias at each iteration. Specifically, at the start of each boosting round, the bias is adjusted as follows:

$$\begin{aligned}&b \leftarrow b + \varDelta _b \end{aligned}$$

(13)

$$\begin{aligned}&\varDelta _b = \frac{1}{2}\log \left( \frac{\sum _{i=1}^n w_i^{(T)} \mathbb {I}(y^{(i)} = +1)}{\sum _{i=1}^n w_i^{(T)} \mathbb {I}(y^{(i)} = -1)}\right) \end{aligned}$$

(14)

This update adjusts the weight distribution to:

$$\begin{aligned} w_i^{(T)} \leftarrow w_i^{(T)}\exp (-y^{(i)}\varDelta _b) \end{aligned}$$

(15)

which has the appealing property of equalizing the weight distribution on positively and negatively labeled examples:

$$\begin{aligned} \sum _{i=1}^n w_i^{(T)} \mathbb {I}(y^{(i)} = -1) = \sum _{i=1}^n w_i^{(T)} \mathbb {I}(y^{(i)} = +1) \end{aligned}$$

(16)

This removes the prevalence bias and forces the learning algorithm to select a classifier with good separation between the two classes.

After T rounds of boosting, we obtain a static ensemble classifier $H(\varvec{x})$. In the following section, we will also require the set of univariate classifiers $f_1(x_1),f_2(x_2),\ldots ,f_p(x_p)$ that comprise this ensemble. These are the weighted sum of decision stumps acting on each of the features. Figure 1 gives an example univariate classifier for the feature noninvasive shock index. So at the end of each boosting round $t=T$, if the selected base classifier operates on feature $x_j$, we update the appropriate univariate classifier $f_j(x_j) \leftarrow f_j(x_j) + \alpha _T h(\varvec{x};\varvec{\theta _T})$. Thus, $H(\varvec{x})$ can be equivalently expressed as $H(\varvec{x})=\sum _{j=1}^p f_j(x_j)$.

Fig. 1

Example univariate classifier for shock index. The blue histogram underlay is the population distribution of shock index

3.2 Dynamic ensemble learning

The goal of the dynamic ensemble is to add a secondary layer of resilience to missing data. Our approach again avoids data imputation and instead trains a secondary learning algorithm to combine the univariate classifiers learned in the previous section. The weighting assigned to each of the classifiers is dynamic: it is a function of the presence/absence measurement pattern of the input features. This allows the classifier to account for certain missing features by adjusting the strength of predictions made by other univariate classifiers.

We illustrate the utility of the approach with an example. Assume, for simplicity, that our classifier $H(\varvec{x})$ from the previous section is composed of three univariate classifiers, $f_1(x_1)$, $f_2(x_2)$, and $f_3(x_3)$:

$$\begin{aligned} H(\varvec{x}) = f_1(x_1) + f_2(x_2) + f_3(x_3) \end{aligned}$$

(17)

and that the three univariate classifiers are approximately linearly dependent so that we may write:

$$\begin{aligned} \beta _1 f_1(x_1) + \beta _2 f_2(x_2) + \beta _3 f_3(x_3) \approx 0 \end{aligned}$$

(18)

for some scalars $\beta _1,\beta _2,\beta _3$. Note that we are not assuming that the underlying variables $x_1,x_2,x_3$ are dependent, only that their univariate classifier predictions are correlated.

Our goal is to most faithfully reproduce the predictions of $H(\varvec{x})$ above in the case of missing data. For example, suppose that a given input pattern $\varvec{x}$ is missing a value for $x_1$ ($x_1=\phi$), which causes $f_1(x_1)$ to abstain. Given the redundancy implied by (18), however, we can account for $f_1(x_1)$ by faithfully reproducing it given $f_2(x_2)$ and $f_3(x_3)$, so that we have:

$$\begin{aligned} H(\varvec{x}=(\phi ,x_2,x_3)) \approx \left( 1 - \frac{\beta _2}{\beta _1}\right) f_2(x_2) + \left( 1 - \frac{\beta _3}{\beta _1}\right) f_3(x_3) \end{aligned}$$

(19)

Similar equations can be derived if $x_2$ or $x_3$ is missing.

Mathematically, we can express our dynamic classifier, $H_d(\varvec{x})$ as follows:

$$\begin{aligned} H_d(\varvec{x})= & {} a_1(\varvec{x}) f_1(x_1) + a_2(\varvec{x}) f_2(x_2) + a_3(\varvec{x}) f_3(x_3) \end{aligned}$$

(20)

$$\begin{aligned} a_1(\varvec{x})= & {} 1 - \frac{\beta _1}{\beta _2} \mathbb {I}(x_2=\phi ) - \frac{\beta _1}{\beta _3} \mathbb {I}(x_3=\phi ) \end{aligned}$$

(21)

$$\begin{aligned} a_2(\varvec{x})= & {} 1 - \frac{\beta _2}{\beta _1} \mathbb {I}(x_1=\phi ) - \frac{\beta _2}{\beta _3} \mathbb {I}(x_3=\phi ) \end{aligned}$$

(22)

$$\begin{aligned} a_3(\varvec{x})= & {} 1 - \frac{\beta _3}{\beta _1} \mathbb {I}(x_1=\phi ) - \frac{\beta _3}{\beta _2} \mathbb {I}(x_2=\phi ) \end{aligned}$$

(23)

where $\mathbb {I}(\cdot )$ is the indicator function. Here, $a_1(\varvec{x}),a_2(\varvec{x}),a_3(\varvec{x})$ are data-dependent weightings for each of the univariate classifiers. This allows the classifier to adjust the strength of individual classifiers based on the measurement pattern to account for other missing features.

The above model requires knowledge of the coefficients $\beta _1,\beta _2,\beta _3$ in (20), which could be estimated via a linear regression. However, instead of learning the correlations between univariate classifiers (as would be achieved by a linear regression), we learn the weighting functions $a_j(\varvec{x})$ directly to maximize classification accuracy. Thus, we treat the $a_j(\varvec{x})$ in (20) as parameters in a second-level classification algorithm that seeks to maximize the accuracy of $H_d(\varvec{x^{(1)}}),\ldots ,H_d(\varvec{x^{(n)}})$ in predicting the category labels $y^{(1)},y^{(2)},\ldots ,y^{(n)}$. This is a more direct approach, since our ultimate goal is to achieve high classification accuracy anyway. In other words, we care to preserve the predictions outputted by $H(\varvec{x})$, not necessarily the actual risk value $H(\varvec{x})$.

Moving away from the example above and into the general case, our classifier from Sect. 3.1 is constructed from all p features and a constant bias, so we have $p+1$ weighting functions to learn:

$$\begin{aligned} H_d(\varvec{x}) = \sum _{j=0}^p a_j(\varvec{x}) f_j(x_j) \end{aligned}$$

(24)

where we denote $x_0=1$ and $f_0(x_0)=b$, the bias term, for simplicity of notation. Given the above discussion, and in particular the expressions (21)–(23) for $a_1(\varvec{x}),a_2(\varvec{x}),a_3(\varvec{x})$ in our toy example, the weighting functions are modeled as:

$$\begin{aligned} a_j(\varvec{x}) = 1 + \sum _{k=1}^p s_{jk}\mathbb {I}(x_k = \phi ),\quad j=0,1,\dots ,p \end{aligned}$$

(25)

Here, $s_{jk}$ represents the adjustment to the weighting on the classifier on feature j to account for feature k being missing. Thus, $s_{jj}=0$, $j=0,1,\ldots ,p$ since a feature cannot account for itself being missing. This results in a total of $p^2-1$ parameters. Also, although each univariate classifier $f_j(x_j)$ is only a function of one variable, its weight $a_j(\varvec{x})$ depends on all of ${\varvec{x}}$ through its measurement pattern $\mathbb {I}(x_1=\phi ),\dots ,\mathbb {I}(x_p=\phi )$.

Given (25), our task in learning $a_0(\varvec{x}),a_1(\varvec{x}),\dots ,a_p(\varvec{x})$ is equivalent to learning the coefficients $s_{jk}, \quad j=0,1,\ldots ,p, \quad k=1,\dots ,p$. Since $H_d(\varvec{x})$ is linear in these coefficients, we can use a standard linear classification algorithm on the augmented set of features $u_{jk}(\varvec{x})$, defined by:

$$\begin{aligned} u_{jk}(\varvec{x}) = f_j(x_j)\mathbb {I}(x_k=\phi ), \quad j=0,1,\ldots ,p, \quad k=1,\dots ,p \end{aligned}$$

(26)

Putting this all together, our dynamic classifier can be expressed as:

$$\begin{aligned} H_d(\varvec{x}) = H(\varvec{x}) + \sum _{j=0}^p \sum _{k=1}^p s_{jk} u_{jk}(\varvec{x}) \end{aligned}$$

(27)

This approach increases the feature space dimension considerably [from O(p) to $O(p^2)$]. Depending on the size of the training dataset (and the disparity between p and n), this increase may lead to overfitting. There are a few ways to overcome this problem, however. First, feature pruning can be applied to the augmented set of features based on the measurement frequency of pairs of features. Since $u_{jk}$ is only “on” when $x_j$ is measured (otherwise $f_j(x_j)$ abstains) and $x_k$ is missing, $u_{jk}$ may be eliminated if this situation arises very infrequently. A natural extension of this idea is to reduce the dimensionality of the feature space by applying principal components analysis (PCA), or a similar technique. Another approach is to incorporate the full augmented feature space, but incorporate a regularization term that penalizes model complexity, such as the ridge or LASSO (Hastie et al. 2009).

Instead, we learn the weighting functions by running a number of supplemental boosting rounds to further reduce the exponential loss function in (3), but we replace the class of weak learners with the augmented set of features $u_{jk}(\varvec{x})$. Thus, at each supplemental boosting round, one of the augmented features is selected and incorporated into $H_d(\varvec{x})$. A benefit of this approach is that the sparsity of the dynamic ensemble coefficients is directly controlled by the number of supplemental boosting rounds run.

However, since the weak learners are no longer binary valued [since the $u_{jk}(\varvec{x})$ are weighted sums of decision stumps], the AdaBoost with abstaining algorithm described in the previous section does not apply. Rather, we use gradient boosting (Mason et al. 1999; Friedman 2001), which selects a weak learner to add at each iteration based on its similarity to the current gradient of the exponential loss objective function (3). Specifically, let $H_d^{(0)}(\varvec{x})=H(\varvec{x})$ denote the dynamic ensemble classifier at the start of the supplemental boosting rounds (i.e., supplemental round $t=0$). Then for supplemental rounds $t=1,\ldots ,T$, we first compute the current weight distribution on the samples:

$$\begin{aligned} w_i^{(t)} = \exp \left( -y^{(i)}H_d^{(t-1)}(\varvec{x^{(i)}})\right) ,\quad i=1,\ldots ,n \end{aligned}$$

(28)

We then select a feature $u^{(t)}(\varvec{x})$ that maximizes the following:

$$\begin{aligned} u^{(t)}(\varvec{x}) = \arg \max _{u_{jk}(\varvec{x})} \left| \sum _{i=1}^n w_i^{(t)} y^{(i)} u_{jk}(\varvec{x^{(i)}}) \right| \end{aligned}$$

(29)

The maximization in (29) selects the augmented feature most correlated with the current gradient vector of the objective, which is given by $\left[ w_1^{(t)}y^{(i)},\dots ,w_n^{(t)}y^{(i)}\right]$. The corresponding weighting assigned to $u^{(t)}(\varvec{x})$, denoted $s^{(t)}$, can be optimized using a line search procedure (Schapire and Singer 1999). Finally, the dynamic classifier is updated:

$$\begin{aligned} H_d^{(t)}(\varvec{x}) = H_d^{(t-1)}(\varvec{x}) + s^{(t)} u^{(t)}(\varvec{x}) \end{aligned}$$

(30)

Incorporating a second-stage algorithm for ensemble learning is similar to the stacking approach in machine learning (Wolpert 1992; Breiman 1996). In particular, our model for the dynamic ensemble weightings in (25) resembles the approach in Sill et al. (2009), which used custom-built meta-features to combine many strong predictive models into an even more powerful one. Our approach instead is specific to the missing data problem and uses the measurement pattern vectors as meta-features to combine simple univariate classifiers into a powerful one that is robust to the missing data. Our optimization approach is also distinct since it is built on the boosting framework.

4 Results

Algorithms to predict hemodynamic instability were trained and validated on the data described in Sect. 2 using 10-fold cross-validation. When splitting the data into cross-validation folds, we were careful to split by hospital, which allows us to test the inter-hospital generalization performance of the classifier. A summary of the classification methods run on these data, including the proposed dynamic ensemble method (referred to as “Dynamic-Abstain-Boost”) are given in Table 3.

Table 3 Description of machine learning algorithms applied to hemodynamic instability prediction

Cross-validated prediction accuracy measures for these techniques are provided in Fig. 2. Due to the problem of alarm fatigue in hospitals, the application stresses the need for indicators with a very low false positive rate (FPR). As a result, the plots focus on high specificity decision thresholds (those with $\text {FPR}<0.05$). Figure 2a, b plot the precision-recall and ROC curves. Table 4 provides the area under the ROC curve (AUC) for each method, along with its partial AUC (pAUC), defined as the AUC restricted to the $\text {FPR}<0.05$ region. For reference, a perfectly accurate classifier has a pAUC of 0.05, while a random classifier (with $\text {AUC}=0.5$) has a pAUC of 0.00125. Based on the application constraints, we view pAUC as the more important measure. Based on the figures and the results in Table 4, Dynamic-Abstain-Boost provides the best prediction accuracy. Interestingly, MI-Boost does not perform better than simple mean imputation (Impute-Boost).

Fig. 2

Cross-validated accuracy measures on the hemodyanmic instability dataset. a Precision-Recall Curves. b ROC Curves ($\text {FPR}<0.05$). c $F_1$ score. d $F_{0.5}$ score

Table 4 AUC and pAUC ($\text {FPR}<0.05$) 1-h before intervention

Since the true prevalence of hemodynamic instability may vary from hospital-to-hospital, we estimated the precision of each classifier for various instability prevalences (assuming fixed sensitivity and specificity) using Bayes’ rule:

$$\begin{aligned} \text {Precision} = \frac{\text {Sensitivity}}{\text {Sensitivity} + (1 - \text {Specificity})(100 - \text {Prevalence})/\text {Prevalence}} \end{aligned}$$

(31)

The prevalence was varied from 1 to 10 %, and for each prevalence value, we calculated the $F_1$ and $F_{0.5}$ scores, defined as:

$$\begin{aligned} F_1= & {} \frac{\text {Precision}\cdot \text {Recall}}{\text {Precision}+\text {Recall}} \end{aligned}$$

(32)

$$\begin{aligned} F_{0.5}= & {} \frac{1.25\cdot \text {Precision}\cdot \text {Recall}}{0.25\cdot \text {Precision}+\text {Recall}} \end{aligned}$$

(33)

The $F_1$ score weighs precision and recall equally, while the $F_{0.5}$ score places a higher emphasis on precision, which is appropriate in this application. Plots of these measures against instability prevalence are provided in Fig. 2c, d. Dynamic-Abstain-Boost is again the clear winner with respect to all 3 of these measures.

We also compared Dynamic-Abstain-Boost to AdaBoost algorithms augmented with features developed from a generative model—Naive Bayes (NB), as proposed by Smeraldi et al. (2010). NB is a natural fit with AdaBoost because the individual feature densities estimated by NB act like univariate classifiers that may be treated as weak learners by AdaBoost. Additionally, being a generative model, NB handles missing data in a natural way.

The NB classifier makes predictions based on the odds ratio $P(y=+1|\mathbf{{x}})/P(y=-1|\mathbf{{x}})$, which factorizes under the assumption of class-conditional independence between features:

$$\begin{aligned} \text {NBC} = \frac{P(y=+1)}{P(y=-1)}\prod _{j=1}^p \frac{P(x_j|y=+1)}{P(x_j|y=-1)} \end{aligned}$$

(34)

Although independence between features is a strong assumption, the benefit of this representation is that it naturally handles missing data: if a feature $x_j$ is missing, its corresponding odds ratio $P(x_j|y=+1)/P(x_j|y=-1)$ is set to 1. The class-conditional densities were estimated from the training data using kernel smoothing (function ksdensity in MATLAB), and the prior odds were estimated empirically.

Abstain-Boost and Dynamic-Abstain-Boost were benchmarked against the 3 different combinations of NB and AdaBoost classifiers listed in Table 5. All algorithms were trained using the same boosting convergence criteria from above. Results were averaged and standard errors were assessed over 5 distinct 10-fold cross-validations, each of which split the data by hospital to test inter-hospital generalization ability. Table 6 lists the AUC and pAUC (FPR $<0.05$) results for all 5 methods. Dynamic-Abstain-Boost produces a significant improvement in both AUC and pAUC (FPR $<0.05$) over the other 4 classifiers considered. The second best classifier is Abstain-Boost+NBWL, which enriches the hypothesis class over Abstain-Boost by incorporating the individual feature odds ratios from NB, but backs off from the stringent NB independence assumption by allowing the AdaBoost algorithm to take into account correlations between feature odds ratios. We also found Abstain-Boost and Abstain-Boost+NBC to provide identical performance. This is because they only differ by incorporating the NBC feature in (34) and this feature was not found to be discriminative due to it greatly over-exaggerating the odds ratio by neglecting feature dependencies.

Table 5 Comparison methods integrating boosting and Naive Bayes (NB)

Table 6 Summary of naive bayes (NB) + Boosting results

4.1 Discussion and interpretation of results

The results show that Dynamic-Abstain-Boost provides a significant improvement in cross-validated prediction accuracy in the presence of missing data over a number of other standard approaches. Aside from statistical significance, however, is also the question of how substantial the improvement is relative to the application domain. In this regard, the improvement is most pronounced where it matters most for this application: the high specificity region of the ROC curve. Due to the problem of alarm fatigue in hospitals, the success of a predictive algorithm hinges on its prediction power under very low false positive rates. To illustrate the improvement benefit, Fig. 3 plots the ROC curve in the low false positive region for Dynamic-Abstain-Boost and the next-best performing classifier, Abstain-Boost+NBWL. At FPR = 0.02, Dynamic-Abstain-Boost offers a 7.5 % improvement in sensitivity (from 33 to 35.5 %). In absolute terms, this amounts to an increased detection of $\approx 130$ hemodynamically unstable patients (2.5 % of 5237 unstable patients). Stated differently, to achieve the same sensitivity as Dynamic-Abstain-Boost, Abstain-Boost+NBWL must increase its FPR to 0.0235, which results in an increase of 154 false positives (0.35 % of 44,019 stable patients).

Fig. 3

High-specificity region of the ROC curve contrasting Dynamic-Abstain-Boost with Abstain-Boost+NBWL

Since the main motivation of this application is for early detection of hemodynamic instability, we also applied the Dynamic-Abstain-Boost classifier to earlier times in each 6-h segment. When evaluating the classifier on a particular segment, we made sure to respect the cross-validation partition so that accuracy results on earlier times are not biased. Table 7 provides a summary of AUC and pAUC results as a function of hours before intervention. As expected, accuracy decreases for earlier times, but even at 6 h before intervention were are able to predict impending hemodynamic instability with an $\text {AUC}>0.8$.

Table 7 Dynamic-Abstain-Boost AUC and pAUC ($\text {FPR}<0.05$) values before intervention

Interpreting the dynamic ensemble coefficients as a strength of association between variables is difficult for a number of reasons. First, the dynamic ensemble learning is driven to maximize classification accuracy when a given feature is absent, not necessarily to imitate the role of that missing feature. Second, a feature’s ensemble weight will only be adjusted to replace another feature if this “replacement” feature is often measured when the other is not. So, for example, although Hemoglobin and Hematocrit are expected to be highly correlated, there are few circumstances where one is measured but not the other—therefore, they have little value in replacing each other. Thus, the algorithm is biased to select “replacement” features that are either measured very frequently or measured exclusively of the missing feature.

Despite this, there are a number of interesting relationships that develop. For example, Lactate is missing on 40,729 (82.7%) of examples. On these cases, the dominant features that are adjusted to account for missing Lactate are Arterial PaCO$_{2}$ (available on 38.3 % of examples when Lactate is missing) and AST (available on 68.1 % of examples when Lactate is missing). Lactate and PaCO$_{2}$ are both related to anaerobic respiration, while Lactate levels and liver function, as indexed by AST, are related to metabolic acidosis (Lian 2010). Another example, Bicarbonate (HCO3) is missing on 25,414 (51.6 %) of examples. On these cases, HCO3 is primarily accounted for by adjusting the Carbon Dioxide predictor (available on 94.2 % of examples when HCO3 is missing). A majority of carbon dioxide in the blood exists in the form of bicarbonate (Fischbach and Dunning 2009).

To isolate and analyze the impact of the dynamic ensemble learning stage on classification performance, we first note that the dynamic ensemble classifier can be interpreted as a family of static ensemble classifiers indexed by the set of $2^p$ missing data patterns. This is true because the ensemble weightings are fixed for all inputs with a common missing data pattern. Specifically, if $H(\varvec{x})=\sum f_j(x_j)$ is the classifier learned by Abstain-Boost, then the secondary dynamic ensemble stage learns a weighting function for each univariate classifier. These weighting functions only depend on the presence/absence pattern in the input $\varvec{x}$; as a result, for a given missing data pattern we obtain a fixed set of weights. Thus, for a fixed missing data pattern, the Dynamic-Abstain-Boost classifier is just a different fixed linear combination of the same univariate classifiers: $H_d(\varvec{x})=\sum a_j f_j(x_j)$.

Given this interpretation, we can compare classification performance restricted to specific missing data patterns to directly test the influence of the dynamic ensemble. This compares the static ensemble Abstain-Boost to a static ensemble from the family defined by Dynamic-Abstain-Boost. In total, there were 15, 662 distinct missing data patterns, many of which occurred only once or a few times across the dataset. As a result, we only compare the two classifiers on the 25 most prevalent missing data patterns. Overall, these 25 missing data patterns accounted for about 20 % of all examples. The missing data patterns considered are provided in Table 8. In general, the most prevalent missing data patterns were missing combinations of invasively measured features, such as central venous pressure and arterial blood gas measurements, as well as white blood cell count profiles. For each missing data pattern, we evaluated the classifier on all samples that had the requisite features measured. For example, if the missing data pattern comprised only having heart rate and systolic blood pressure measured, then the classifiers were re-evaluated on all data samples that had a heart rate and systolic blood pressure measurement, disregarding all other features even if they were measured. This resulted in a much larger sample size for each pattern to compare the classifiers on. Figure 4a compares the cross-validated partial AUC ($\text {FPR}<0.05$) values for Abstain-Boost and Dynamic-Abstain-Boost for each of the 25 missing data patterns. Dynamic-Abstain-Boost provides a measurable improvement on 24 of the 25 patterns.

Fig. 4

Comparison of Abstain-Boost and Dynamic-Abstain-Boost on the 25 most prevalent missing data patterns on the hemodynamic instability dataset. a Partial AUC ($\text {FPR}<0.05$) for the 25 most prevalent missing data patterns. b EMD between class-conditional distributions for the 25 most prevalent missing data patterns

Table 8 The 25 most prevalent missing data patterns in the hemodynamic instability dataset (+indicates feature is measured)

Aside from comparing standard metrics of accuracy, we also compared the distance between the class-conditional distributions of the classifier outputs on each of the missing data patterns, which provides insight on the margin of separation between categories. Specifically, we computed $p(H(\varvec{x})|y=0)$ and $p(H(\varvec{x})|y=1)$ for Abstain-Boost and $p(H_d(\varvec{x})|y=0)$ and $p(H_d(\varvec{x})|y=1)$ for Dynamic-Abstain-Boost. These distributions were developed using classifier predictions on out-of-fold (test) samples. To quantify the distance between class-conditional distributions, we used the Earth Mover’s Distance (EMD) (Peleg et al. 1989). The name arises from considering the two distributions as piles of dirt: EMD then equals the amount of work required to transform one pile of dirt into the other (here, “work” equals the amount of dirt moved times the distance traveled). In one dimension, it can be shown that the EMD between two probability distributions is equal to the area between their respective cumulative distribution functions (Cohen and Guibas 1997). Figure 4b compares the EMD between class-conditional distributions for Abstain-Boost and Dynamic-Abstain-Boost on each of the 25 most prevalent missing data patterns. Dynamic-Abstain-Boost provides a significant increase in EMD on all 25 patterns.

5 Conclusion

We proposed a principled and simple two-stage machine learning algorithm that learns a dynamic classifier ensemble from an incomplete dataset without data imputation. The ensemble offers resilience to missing data by adjusting the strength of predictions of certain classifiers to account for missing features. We validated our approach on a real dataset to predict hemodynamic instability in adult ICU patients. Our results show that predictive algorithms can detect instability early (up to 6 h before an intervention), providing the clinician additional time to evaluate patient state and decide on intervention therapy.