Good edit similarity learning by loss minimization

Abstract

Similarity functions are a fundamental component of many learning algorithms. When dealing with string or tree-structured data, measures based on the edit distance are widely used, and there exist a few methods for learning them from data. However, these methods offer no theoretical guarantee as to the generalization ability and discriminative power of the learned similarities. In this paper, we propose an approach to edit similarity learning based on loss minimization, called GESL. It is driven by the notion of (ϵ,γ,τ)-goodness, a theory that bridges the gap between the properties of a similarity function and its performance in classification. Using the notion of uniform stability, we derive generalization guarantees that hold for a large class of loss functions. We also provide experimental results on two real-world datasets which show that edit similarities learned with GESL induce more accurate and sparser classifiers than other (standard or learned) edit similarities.

1 Introduction

Using an appropriate pairwise similarity or distance function is key to many supervised and unsupervised learning methods, among which the popular k-Nearest Neighbors, K-Means and Support Vector Machines. For this reason, a lot of research has gone into automatically learning them from data, which is often referred to as similarity learning. When data is made of vectors in ℝⁿ, a common approach is to learn the transformation matrix of a Mahalanobis distance (Yang and Jin 2006; Davis et al. 2007; Weinberger and Saul 2009; Jin et al. 2009; Bian and Tao 2011). Some of these methods have nice statistical properties that allow the derivation of generalization bounds, ensuring the good behavior of the resulting similarity function on unseen data (Jin et al. 2009; Bian and Tao 2011).

However, in many cases (such as in natural language processing, bioinformatics or web document classification, among others), data may be string or tree-structured and one needs similarity measures that take into account this structure. In this context, edit distance-based similarity functions are widely used by practitioners. Roughly speaking, the edit distance between two objects is the cost of the best sequence of operations (insertion, deletion, substitution of a symbol) required to transform an object into another, where an edit cost is assigned to each possible operation. Although they involve complex procedures, there exist a few methods for learning edit similarities (i.e., learning the edit costs) for a given task. Most general-purpose methods maximize the likelihood of the data using EM-like iterative algorithms (Ristad and Yianilos 1998; Bilenko and Mooney 2003; McCallum et al. 2005; Oncina and Sebban 2006; Bernard et al. 2008; Mehdad 2009; Takasu 2009), which can imply a costly learning phase. Saigo et al. (2006) manage to avoid this drawback in the context of remote homologies detection in protein sequences by applying gradient descent to a specific objective function. Unfortunately, these approaches share several drawbacks. Some of them do not guarantee to find the optimal parameters and/or are based on a training set of positive pairs only: they do not take advantage of pairs of examples that have different labels. Above all, the generalization ability of the resulting edit similarity is not guaranteed, and it is therefore unclear whether it will actually lead to better performance for the classification or clustering task at hand.

Recently, Balcan et al. (2006, 2008) introduced a theory of learning with so-called (ϵ,γ,τ)-good similarity functions that gives intuitive, sufficient conditions for a similarity function to allow one to learn well. Essentially, a similarity function K is (ϵ,γ,τ)-good if a 1−ϵ proportion of examples are on average 2γ more similar to reasonable examples of the same class than to reasonable examples of the opposite class, where a τ proportion of examples must be reasonable. K does not have to be a metric nor positive semi-definite (PSD). They show that if K is (ϵ,γ,τ)-good, then it can be used to build a linear separator in an explicit projection space that has margin γ and error arbitrarily close to ϵ. This separator can be learned efficiently using a linear program and tends to be sparse thanks to L ₁-norm regularization. The work of Bellet et al. (2011a) has experimentally shown that this framework is well suited to the use of edit similarities.

In this article, we propose a new framework for learning edit similarities which addresses the drawbacks of other methods in the literature. Our approach (GESL, for Good Edit Similarity Learning) is driven by the idea of (ϵ,γ,τ)-goodness: we learn the edit costs so as to optimize the goodness of the resulting similarity function. It is based on loss minimization and formulated as an efficient convex program. We provide an extensive theoretical study of the properties of GESL based on the notion of uniform stability (Bousquet and Elisseeff 2002) leading to the derivation of a generalization bound that holds for a large class of loss functions. This bound guarantees that our learned similarity will induce low-error classifiers for the task at hand and is independent of the size of the alphabet, making GESL suitable for handling problems with large alphabet. To the best of our knowledge, this constitutes the first attempt to establish a theoretical relationship between a learned edit similarity function and its generalization and discriminative power. We show in a comparative experimental study on two real-world datasets that GESL has fast convergence and leads to more accurate and sparser classifiers than other (standard or learned) edit similarities.

This paper builds upon an earlier conference paper (Bellet et al. 2011b), which was a first attempt at learning edit similarity functions so as to optimize their (ϵ,γ,τ)-goodness. This journal version presents these previous results with detailed explanations, more extensive experiments and improved presentation. It also features several important new contributions: the extension of our method to general loss functions, its adaptation to tree-structured data and the generalization of our theoretical analysis to examples of unbounded size.

This paper is organized as follows. In Sect. 2, we introduce some background and notations, focusing on the theory of (ϵ,γ,τ)-goodness and the notion of edit distance. Section 3 reviews some prior work on string edit similarity learning. In Sect. 4, we present GESL, our approach to learning (ϵ,γ,τ)-good edit similarities. We show that it is a suitable way to deal not only with strings but also with tree-structured data. We propose in Sect. 5 a theoretical analysis of GESL based on uniform stability, leading to the derivation of a generalization bound that holds for a large class of loss functions. We also provide a discussion on that bound and its implications, as well as a way of deriving a bound when dealing with examples of unbounded size. A wide experimental evaluation of our approach on two real-world string datasets from the natural language processing and image classification domains is provided in Sect. 6. Finally, we conclude this work by outlining promising lines of research on similarity learning.

2 Background

We consider the following binary classification problem: we are given some labeled examples z=(x,ℓ) drawn from an unknown distribution P over X×{−1,1}, where X is the instance space. We want to learn a classifier h:X→{−1,1} whose error rate is as low as possible using pairwise similarities according to a similarity function K:X×X→[−1,1]. We say that K is symmetric if for all x,x′∈X, K(x,x′)=K(x′,x). K is a valid (or Mercer) kernel if it is symmetric and PSD.

2.1 Learning with good similarity functions

In recent work, Balcan et al. (2006, 2008) introduced a new theory of learning with good similarity functions. Their motivation was to overcome two major limitations of kernel theory. First, a good kernel is essentially a good similarity function, but the theory talks in terms of margin in an implicit, possibly unknown projection space, which can be a problem for intuition and design. Second, the PSD and symmetry requirement often rules out natural similarity functions for the problem at hand. As a consequence, Balcan et al. (2008) proposed the following definition of good similarity function.

Definition 1

(Balcan et al. 2008)

A similarity function K:X×X→[−1,1] is an (ϵ,γ,τ)-good similarity function for a learning problem P if there exists a (random) indicator function R(x) defining a (probabilistic) set of “reasonable points” such that the following conditions hold:

• 1. A 1−ϵ probability mass of examples (x,ℓ) satisfy

  $$\mathbf{E}_{(x',\ell')\sim P}\bigl[\ell\ell'K\bigl(x,x'\bigr)|R\bigl(x'\bigr)\bigr]\geq\gamma. $$

• 2. Pr _x′[R(x′)]≥τ.

The first condition is essentially requiring that a 1−ϵ proportion of examples x are on average 2γ more similar to random reasonable examples of the same class than to random reasonable examples of the opposite class and the second condition that at least a τ proportion of the examples are reasonable. Figure 1 gives a graphical insight into the definition.

Fig. 1

A graphical insight into Definition 1. Let us consider the points shown above and take the similarity function K to be minus the normalized Euclidean distance. Distances to the reasonable points are given in the array. We can set τ=3/8 since 3 points out of 8 are reasonable. There exists an infinite number of valid instantiations of ϵ and γ since there is a trade-off between the margin γ and proportion of margin violations ϵ. For example, K is (0,0.03,3/8)-good because all points (ϵ=0) are on average 2γ=0.06 more similar to reasonable examples of the same class than to reasonable examples of the other class. One can also say that K is (1/8,0.12,3/8)-good (ϵ=1/8 because example E violates the margin γ=0.12)

Note that other definitions are possible, like those proposed by Wang et al. (2007) for unbounded dissimilarity functions. Yet Definition 1 is very interesting in two respects. First, it includes all good kernels as well as some non-PSD similarity functions. In that sense, this is a strict generalization of the notion of good kernel (Balcan et al. 2008). Second, these conditions are sufficient to learn well, i.e., to induce a linear separator α in an explicit space that has low-error relative to L ₁-margin γ. This is formalized in Theorem 1.

Theorem 1

(Balcan et al. 2008)

Let K be an (ϵ,γ,τ)-good similarity function for a learning problem P. Let $S = \{x_{1}',x_{2}',\dots,x_{d}'\}$ be a (potentially unlabeled) sample of $d=\frac{2}{\tau} (\log(2/\delta )+8\frac{\log(2/\delta)}{\gamma^{2}} )$ landmarks drawn from P. Consider the mapping ϕ ^S:X→ℝ^d defined as follows: $\phi^{S}_{i}(x) = K(x,x_{i}')$, i∈{1,…,d}. Then, with probability at least 1−δ over the random sample S, the induced distribution ϕ ^S(P) in ℝ^d has a linear separator of error at most ϵ+δ relative to L ₁ margin at least γ/2.

Therefore, if we are given an (ϵ,γ,τ)-good similarity function for a learning problem P and enough (unlabeled) landmark examples, then with high probability there exists a low-error linear separator α in the explicit “ϕ-space”, which is the space of the similarities to the d landmarks (see Fig. 2 for an example).

Fig. 2

The projection space (ϕ-space) implied by the example from Fig. 1: similarity scores to the reasonable points (A, C and G) are used as features. The linear separator α is also shown as a dotted grid

Unfortunately, finding this separator α is NP-hard (even to approximate) because minimizing the number of L ₁-margin violations is NP-hard. To overcome this limitation, the authors considered the hinge loss instead of the margin error in the following reformulation of Definition 1:

Definition 2

(Balcan et al. 2008)

A similarity function K:X×X→[−1,1] is an (ϵ,γ,τ)-good similarity function in hinge loss for a learning problem P if there exists a (random) indicator function R(x) defining a (probabilistic) set of “reasonable points” such that the following conditions hold:

• 1. E _(x,ℓ)∼P [[1−ℓg(x)/γ]₊]≤ϵ, where g(x)=E _{(x′,ℓ′)∼P} [ℓ′K(x,x′)|R(x′)] and [1−c]₊=max(0,1−c) is the hinge loss,

• 2. Pr _x′[R(x′)]≥τ.

This leads to the following theorem, similar to Theorem 1.

Theorem 2

(Balcan et al. 2008)

Let K be an (ϵ,γ,τ)-good similarity function in hinge loss for a learning problem P. For any ϵ ₁>0 and 0≤δ≤γϵ ₁/4, let $S = \{x_{1}',x_{2}',\dots,x_{d}'\}$ be a (potentially unlabeled) sample of $d=\frac{2}{\tau}(\log(2/\delta)+16\frac{\log(2/\delta)}{\epsilon _{1}\gamma^{2}})$ landmarks drawn from P. Consider the mapping ϕ ^S:X→ℝ^d defined as follows: $\phi^{S}_{i}(x) = K(x,x_{i}')$, i∈{1,…,d}. Then, with probability at least 1−δ over the random sample S, the induced distribution ϕ ^S(P) in ℝ^d has a linear separator of error at most ϵ+ϵ ₁ at margin γ.

The objective is now to find a linear separator α∈ℝ^d that has low error based on the expected hinge loss relative to L ₁-margin γ:

$$\mathbf{E}_{(x,\ell)\sim P}\bigl[\bigl[1 - \ell\big\langle \boldsymbol{\alpha},\phi^S(x) \big\rangle/\gamma\bigr]_+\bigr]. $$

Using d _u unlabeled examples and d _l labeled examples, one can find this separator $\boldsymbol{\alpha}\in\mathbb{R}^{d_{u}}$ by solving the following linear program (LP):¹

$$ \displaystyle\min_{\boldsymbol{\alpha}} \displaystyle\sum_{i=1}^{d_l} \Biggl[1-\sum_{j=1}^{d_u} \alpha_j\ell_iK\bigl(x_i,x'_j \bigr) \Biggr]_+ + \lambda\|\boldsymbol{\alpha}\|_1. $$

(1)

Note that (1) is essentially a 1-norm SVM problem (Zhu et al. 2003) with an empirical similarity map (Balcan and Blum 2006), and can be efficiently solved. An important feature of (1) is the L ₁-regularization on α, which induces sparsity, as opposed to L ₂-regularization (see Figure 3 for a geometric interpretation). It allows automatic selection of reasonable points among the available landmarks, ignoring the others (whose corresponding coordinates in α will be set to zero during learning). Therefore, one does not need to know in advance the set of reasonable points R: it is automatically worked out while learning α. We can also control the sparsity of the solution: the larger λ, the sparser α.

Fig. 3

Geometric interpretation of L ₂ and L ₁ constraints, adapted from Bach and Obozinski (2010). The L ₁-norm tends to zero out coordinates, thus reducing dimensionality. This intuition also holds in the case of regularization

Our objective in this paper is to make use of this theory to efficiently learn (ϵ,γ,τ)-good edit similarities from data that will lead to effective classifiers.

2.2 String edit distance

The classic edit distance, known as the Levenshtein distance (Levenshtein 1966), is defined as follows.

Definition 3

The Levenshtein distance e _L (x,x′) between two strings x=x ₁⋯x _m and $x'=x'_{1} \cdots x'_{n}$ of length m and n respectively is the minimum number of edit operations to change x into x′. The allowable operations are insertion, deletion and substitution of a symbol. e _L can be computed in O(mn) time using dynamic programming.

Instead of only counting the minimum number of required operations, we can set a cost (or probability) for each edit operation. These parameters are usually represented as a positive cost matrix C of size (A+1)×(A+1), where A is the size of $\mathcal{A}$, the alphabet x and x′ have been generated from (the additional row and column account for insertion and deletion costs respectively). C _i,j gives the cost of the operation changing the symbol c _i into c _j , c _i and c _j $\in\mathcal{A} \cup\{\$\}$, where $ is the empty symbol. Given C, a generalized edit similarity e _C can be defined as being the cost corresponding to the sequence of minimum cost. This sequence is called the optimal edit script.

3 Related work on string edit similarity learning

Using a matrix C that is appropriately tuned to the considered task can lead to significant improvements in performance. For some applications, such matrices may be available, like BLOSUM in the context of protein sequence alignment (Henikoff and Henikoff 1992). However, in most domains it is not the case, and tuning the costs manually is difficult. For this reason, methods for learning C from data have attracted a lot of interest. Most general-purpose approaches take the form of probabilistic models. Parameter estimation methods of edit transducers were used to infer generative (Ristad and Yianilos 1998; Bilenko and Mooney 2003; Takasu 2009) or discriminative models (Oncina and Sebban 2006).

Note that the above approaches use an Expectation-Maximization (EM)-like algorithm (Dempster et al. 1977) to estimate the parameters of probabilistic models. Beyond the fact that EM is not guaranteed to converge to a global optimum, it can also cause two major drawbacks in the context of edit distance learning. First, since EM is iterative, parameter estimation and distance calculations must be performed several times until convergence, which can be expensive to compute, especially when the size of the alphabet and/or the length of the strings are large. Second, by maximizing the likelihood of the data, one only considers pairs of strings of the same class (positive pairs) while it may be interesting to make use of the information brought by pairs of strings that have a different label (negative pairs). As a consequence, the above methods “move closer together” examples of the same class, without trying to also “move away from each other” examples of different class. McCallum et al. (2005) consider discriminative conditional random fields, dealing with positive and negative pairs in specific states, but still using EM for parameter estimation. To overcome the drawback of iterative approaches for the task of detecting remote homology in protein sequences, Saigo et al. (2006) optimize by gradient descent an objective function meant to favor the discrimination between positive and negative examples. But this is done by only using positive pairs of distant homologs.

Despite their diversity, a common feature shared by all of the above approaches is that they do not optimize similarity functions to be (ϵ,γ,τ)-good and thus do not take advantage of the theoretical results of Balcan et al. (2008). In other words, there is no theoretical guarantee that the learned edit functions will lead to better performance for the classification or clustering task at hand. In the following, we propose a loss minimization-based edit similarity learning approach, GESL, that bridges this gap.

4 Learning (ϵ,γ,τ)-good edit similarity functions

In this section, we propose a novel convex programming approach based on the theory of Balcan et al. (2008) to learn (ϵ,γ,τ)-good edit similarity functions from both positive and negative pairs without requiring a costly iterative procedure. We will see in Sect. 5 that this framework allows us to derive generalization bounds establishing the consistency of our method and a relationship between the learned similarities and their (ϵ,γ,τ)-goodness.

We begin this section by introducing an exponential-based edit similarity function that can be optimized in a direct way. Then, we present our convex programming approach to the problem of learning (ϵ,γ,τ)-good edit similarity functions, followed by a discussion on building relevant training pairs in this context. Finally, we end this section by showing that our approach can be straightforwardly adapted to tree edit similarity learning.

4.1 An exponential-based edit similarity function

What makes the edit cost matrix C hard and expensive to optimize is the fact that the edit distance is based on an optimal script which depends on the edit costs themselves. This is the reason why, as we have seen earlier, iterative approaches are very commonly used to learn C from data. In order to avoid this drawback, we propose to define an edit similarity for which the edit script does not depend on the edit costs.

Let #(x,x′) be an (A+1)×(A+1) matrix whose elements # _i,j (x,x′) are the number of times each edit operation (i,j) is used to turn x into x′ in the optimal Levenshtein script, 0≤i,j≤A. We define the following edit function:

$$e_G\bigl(x,x'\bigr) = \displaystyle\sum_{0 \leq i,j \leq A}C_{i,j}\#_{i,j}\bigl(x,x'\bigr). $$

To compute e _G , we do not extract the optimal script with respect to C: we use the Levenshtein script² and apply custom costs C to it. Therefore, since the edit script defined by #(x,x′) is fixed, e _G (x,x′) is nothing more than a linear function of the edit costs and can be optimized directly.

Recall that in the theory of (ϵ,γ,τ)-goodness, a similarity function must be in [−1,1]. To respect this requirement, we define our similarity function to be:

$$K_G\bigl(x,x'\bigr) = 2e^{-e_G(x,x')}-1. $$

Beyond this normalization requirement, the motivation for this exponential form is related to the one for using exponential kernels in SVM classifiers: it can be seen as a way to introduce nonlinearity to further separate examples of opposite class while moving closer those of the same class. Note that K _G may not be PSD nor symmetric. However, as we have seen earlier, the theory of Balcan et al. (2008) does not require these properties, unlike SVM. This allows us to consider a broader type of edit similarity functions.

4.2 Learning the edit costs

We aim at learning the edit cost matrix C so as to optimize the (ϵ,γ,τ)-goodness of K _G . We first focus on optimizing the goodness according to Definition 2, leading to a formulation based on the hinge loss (GESL _HL ). Then, we introduce a more general version that can accommodate other loss functions (GESL _V ).

4.2.1 Hinge loss formulation

Here, we want to learn K _G so that its hinge loss-based goodness (Definition 2) is optimized. It would be tempting to try to find a way to directly optimize Definition 2. Unfortunately, this is very difficult because it would result in a non-convex formulation (summing and subtracting up exponential terms). Instead, we propose to optimize the following criterion:

$$ \mathbf{E}_{(x,\ell)} \bigl[\mathbf{E}_{(x',\ell')} \bigl[ \bigl[1-\ell\ell'K_G\bigl(x,x' \bigr)/\gamma\bigr]_+|R\bigl(x'\bigr) \bigr] \bigr]\leq \epsilon'. $$

(2)

Criterion (2) bounds that of Definition 2 due to the convexity of the hinge loss. It is harder to satisfy since the “goodness” is required with respect to each reasonable point instead of considering the average similarity to these points. Clearly, if K _G satisfies (2), then it is (ϵ,γ,τ)-good in hinge loss with ϵ≤ϵ′.

Let us now consider a training sample of N _T labeled points $T = \{ z_{i}=(x_{i},\ell_{i})\}_{i=1}^{N_{T}}$. Recall that we do not know the set of reasonable points at this stage: they are inferred while learning the separator, that is, after the similarity is learned. For this reason, as in most similarity learning methods, we will optimize criterion (2) over some pairs of examples, trying to move closer paired examples of the same class and to move away those of opposite class. Formally, we suppose the existence of an indicator pairing function f _land :T×T→{0,1} which takes as input two training examples in T and returns 1 if they are paired and 0 otherwise. We assume that f _land associates to each element z∈T exactly N _L examples (called the landmarks for z), leading to a total of N _T N _L pairs. We discuss this matter further in Sect. 4.3.

As we said, our formulation requires the goodness for each (z _i ,z _j ) such that f _land (z _i ,z _j )=1. Therefore, we want [1−ℓ _i ℓ _j K _G (x _i ,x _j )/γ]₊=0, hence ℓ _i ℓ _j K _G (x _i ,x _j )≥γ. A benefit from using this constraint is that it can easily be turned into an equivalent linear one, considering the following two cases.

• 1. If ℓ _i ≠ℓ _j , we get:

  $$-K_G(x_i,x_j) \geq\gamma\quad\Longleftrightarrow\quad e^{-e_G(x_i,x_j)} \leq\frac{1-\gamma}{2} \quad\Longleftrightarrow\quad e_G(x_i,x_j) \geq -\log\biggl(\frac{1-\gamma}{2}\biggr). $$

  We can use a variable B ₁≥0 and write the constraint as e _G (x _i ,x _j )≥B ₁, with the interpretation that $B_{1} = -\log(\frac {1-\gamma}{2})$. In fact, $B_{1} \geq-\log(\frac{1}{2})$.

• 2. Likewise, if ℓ _i =ℓ _j , we get $e_{G}(x_{i},x_{j}) \leq-\log (\frac{1+\gamma}{2})$. We can use a variable B ₂≥0 and write the constraint as e _G (x _i ,x _j )≤B ₂, with the interpretation that $B_{2} = -\log(\frac {1+\gamma}{2})$. In fact, $B_{2} \in [0,-\log(\frac{1}{2}) ]$.

The optimization problem GESL _HL can then be expressed as follows:

where β≥0 is a regularization parameter on edit costs, $\| \cdot\|_{\mathcal{F}}$ denotes the Frobenius norm (which corresponds to the L ₂-norm when considering a matrix as a n×n vector) and η _γ ≥0 a parameter corresponding to the desired “margin”. The relationship between the margin γ and η _γ is given by $\gamma=\frac{e^{\eta_{\gamma}}-1}{e^{\eta_{\gamma}}+1}$.

GESL _HL is a convex program, thus one can efficiently find its global optimum. Using N _T N _L slack variables to express each hinge loss, it has O(N _T N _L +A ²) variables and O(N _T N _L ) constraints. Note that GESL _HL is quite sparse: each constraint involves at most one string pair and a limited number of edit cost variables, making the problem faster to solve. It is also worth noting that our approach is very flexible. First, it is general enough to be used with any definition of e _G that is based on an edit script (or even a convex combination of edit scripts). Second, one can incorporate additional convex constraints, for instance to include background knowledge or desired requirements on C (e.g., symmetry). Third, it can be easily adapted to the multi-class case. Finally, it can be generalized to a larger class of loss functions, as we show in the following section.

4.2.2 General formulation

In the previous section, we made use of the hinge loss-based Definition 2 to propose GESL _HL . Yet, other reformulations of Definition 1 are possible using any convex loss function that can be used to efficiently penalize the amount of violation ϵ with respect to margin γ. This would also allow the derivation of learning guarantees (similar to Theorem 2) and an efficient learning rule. For instance, the log loss or the quadratic loss for classification could be used. An interesting comparison of loss functions is provided by Rosasco et al. (2004).

Therefore, it is useful to be able to optimize a definition of (ϵ,γ,τ)-goodness based on a loss other than the hinge. Let V(C,z,z′) be a convex loss function for an edit cost matrix C with respect to a pair of examples (z,z′). Our optimization problem can then be expressed in a more general form as follows:

$$ (\mathit{GESL}_{V})\quad\displaystyle\min_{C} \quad\frac {1}{N_TN_L}\displaystyle\sum_{\substack{1\leq i\leq N_T,\\j \mathrm{~s.t.~} f_{land}(z_i,z_j)=1}}V(C,z_i,z_j)+\beta\| C\|^2_{\mathcal{F}}. $$

In the rest of the paper, we will use GESL to refer to our approach in general, GESL _V when using a loss function V and GESL _HL for the specific case of the hinge loss.

4.3 Pairing strategy

The question of how one should define the pairing function f _land relates to the open question of building training pairs in many similarity learning problems. In some applications, the answer may be trivial: for instance, a misspelled word and its correction. Otherwise, popular choices are to pair each example with its nearest neighbor, random pairing or simply to consider all possible pairs.

On the other hand, the (ϵ,γ,τ)-goodness similarity should be improved with respect to the reasonable points, a subset of examples of probability τ that allows low error and large margin. However, this set depends on the similarity function itself and is thus unknown beforehand. Yet, a relevant strategy in the context of (ϵ,γ,τ)-goodness may be to improve the similarity with respect to carefully selected examples (the landmarks) rather than considering all possible pairs. Consequently, we consider two pairing strategies that will be compared in our experiments (Sect. 6):

• 1. Levenshtein pairing: we pair each z∈T with its M nearest neighbors of the same class and its M farthest neighbors of the opposite class, using the Levenshtein distance. This pairing strategy is meant to capture the essence of Definition 1 and in particular the idea that reasonable points “represent” the data well. Essentially, we pair z with a few points that are already good representatives of z and optimize the edit costs so that they become even better representatives. Note that the choice of the Levenshtein distance to pair examples is consistent with our choice to define e _G according to the Levenshtein script.

• 2. Random pairing: we pair each z∈T with a number M of randomly chosen examples of the same class and M randomly chosen examples of the opposite class.

In either case, we have N _L =2M=αN _T with 0<α≤1. Taking α=1 corresponds to considering all possible pairs.

4.4 Adaptation to trees

So far, we have implicitly considered that the data were strings. In this section, before presenting a theoretical analysis of GESL, we show that it may be used in a straightforward way to learn tree edit similarities, which can be of great value. Indeed, there is a growing interest in diverse areas for tree-structured data, due to the applications which naturally involve trees, such as information extraction from the web, computational biology, computer vision, natural language processing, just to name a few. For example, the hierarchical structure of trees appears to be more suited (than feature vectors or flat representation such as strings) for modeling web pages (XML, HTML), the RNA secondary structure of a molecule or phylogenetic processes. Dealing with those applications requires efficient tree comparison. In this context, many approaches have extended the string edit distance to trees (Bille 2005), resorting to the same elementary edit operations.

Like in the case of strings, the tree edit distance can be efficiently computed using dynamic programming. When considering two rooted ordered trees of sizes m and n, where m<n, the best known algorithms for this problem, due to Zhang and Shasha (1989) and Klein (1998), have an O(n ³logn) time complexity and an O(mn) space complexity. In these approaches, when a tree node is deleted, all its children are connected to its father. A less costly variant of these algorithms has been proposed by Selkow (1977), where deleting a node leads to the removal of the entire (sub)tree rooted at that node. The insertion of a (sub)tree is also allowed requiring the iterative insertion of its nodes. Such a distance is relevant to specific applications. For instance, it would make no sense to delete a <UL> tag (i.e., a node) of an unordered list in an HTML document without removing the <LI> items (i.e., the subtree). In this case, the tree edit distance can be computed by dynamic programming in cubic time.

Few methods have been proposed in the literature to automatically learn the edit cost matrix of a tree edit distance, mostly because of algorithmic constraints. Bernard et al. (2008) optimize the parameters of a stochastic edit transducer to learn a probabilistic edit similarity using an EM-based approach. Neuhaus and Bunke (2004) learn a (more general) graph edit distance, where each edit operation is modeled by a Gaussian mixture density whose parameters are learned using an EM-like algorithm. Zigoris et al. (2006) make use of a variant of SVM to learn a parameterized tree alignment model for extracting fields from HTML search results. They design an optimization problem which is difficult to solve directly because the edit distance is a function of a hidden variable. To solve this problem they also use a very time-consuming EM-like algorithm which becomes intractable when the trees get large. Finally, Mehdad (2009) proposes a method based on the Particle Swarm Optimization. The edit costs are learned via an iterative process which (i) may not induce a true metric and (ii) is not provably effective.

As mentioned in Sect. 4.1, our edit function, defined as

$$e_G\bigl(x,x'\bigr) = \sum_{0 \leq i,j \leq A}C_{i,j}\#_{i,j}\bigl(x,x'\bigr), $$

is nothing more than a linear combination of the edit costs, where # _i,j (x,x′) is the number of times the edit operation (i,j) occurs in the Levenshtein script turning x into x′. This opens the door to a straightforward generalization of GESL to tree edit distance: instead of a Levenshtein string edit script, we can use a Levenshtein tree edit script (Zhang and Shasha 1989; Klein 1998; Selkow 1977) and solve the (otherwise unchanged) optimization problem presented in Sect. 4.2. This allows us, once again, to avoid using a costly iterative procedure. We only have to compute the edit script between two trees once, which dramatically reduces the algorithmic complexity of the learning algorithm. Moreover, we will see that the theoretical analysis of GESL presented in the following section holds for tree edit similarity learning.

5 Theoretical analysis of GESL

This section presents a theoretical analysis of GESL. In Sect. 5.1, we derive a generalization bound guaranteeing not only its consistency but also the overall (ϵ,γ,τ)-goodness of the learned edit similarity function for the task at hand. This theoretical study is performed for a large class of loss functions. In Sect. 5.2, we instantiate this generalization bound for the specific case of the hinge loss (GESL _HL ). Finally, Sect. 5.3 is devoted to a discussion about the main features of the bounds, and to the presentation of a way to get rid of the assumption that the size of the examples is bounded.

5.1 Generalization bound for general loss functions

Considering that the pairs $(z_{i},z'_{j})$ used to learn C in GESL _V are not i.i.d., the classic results of statistical learning theory do not directly hold. To derive a generalization bound, extending the ideas of Jin et al. (2009) and Bousquet and Elisseeff (2002) to edit similarity learning, we first prove that our learning method has a uniform stability. This is established in Theorem 3 using Lemma 1 and the hypothesis of k-lipschitzness (Definition 4). The stability property allows us to derive our generalization bound (Theorem 5) using the McDiarmid inequality (Theorem 4) and the assumption of (σ,m)-admissibility (Definition 5).

We denote the objective function of GESL _V by:

$$F_T(C)= \frac{1}{N_T}\sum_{k=1}^{N_T} \frac{1}{N_L}\sum_{j=1}^{N_L} V\bigl(C,z_k,z'_{k_j}\bigr)+\beta\|C\|^2_{\mathcal{F}}, $$

where $z'_{k_{j}}$ denotes the jth landmark associated to z _k and $V(C,z_{k},z'_{k_{j}})$ the loss for a pair of examples with respect to an edit cost matrix C.

The first term of F _T (C), denoted L _T (C) in the following, is the empirical loss over the training sample T. Let us also define the loss over the true distribution P, denoted L(C), and the estimation error D _T as follows:

$$L(C)=\mathbf{E}_{(z,z')\sim P}\bigl[V\bigl(C,z,z'\bigr)\bigr] ; \qquad D_T=L(C_T)-L_T(C_T), $$

where C _T denotes the edit cost matrix learned by GESL _V from T. Recall that our empirical loss is not defined over all possible pairs, unlike most metric learning algorithms, but according to some particular landmark examples. However the true expected loss is defined over any pair of examples.

In this section, we propose an analysis that holds for a large class of loss functions. We consider loss functions V that fulfill the k-Lipschitz property with respect to the first argument C (Definition 4) and the definition of (σ,m)-admissibility (Definition 5).

Definition 4

A loss function V(C,z ₁,z ₂) is k-Lipschitz with respect to its first argument if for any matrices C,C′ and any pair of labeled examples (z ₁,z ₂):

$$\big|V(C,z_1,z_2)-V\bigl(C',z_1,z_2\bigr)\big|\leq k\big\|C-C'\big\|_{\mathcal{F}}. $$

Definition 5

A loss function V(C,z ₁,z ₂) is (σ,m)-admissible, with respect to C, if (i) it is convex with respect to its first argument and (ii) the following condition holds:

$$\forall z_1, z_2, z_3, z_4,\quad\big|V(C,z_1,z_2)-V(C,z_3,z_4)\big |\leq\sigma|l_1l_2-l_3l_4|+m $$

with z _i =(x _i ,l _i ), for i=1,2,3,4, are labeled examples.

Definition 5 requires, with respect to a model C, the deviation of the losses between two pairs of examples to be bounded by a value that depends only on the labels and some constants independent from the examples and the model. It follows that the labels must be bounded, which is not a strong assumption in the classification setting we are interesting in. In our case, we have binary labels (l _i ∈{−1,1}), which implies that the quantity |l ₁ l ₂−l ₃ l ₄| is either 0 or 2. We will see in Sect. 5.2 that the hinge loss of GESL _HL satisfies Definitions 4 and 5. This can also be shown for other popular loss functions, such as the log loss or the quadratic loss for classification.³

Note that from the convexity of V with respect to its first argument, it follows that L, L _T and F _T are convex functions.

Our objective is to derive an upper bound on the generalization loss L(C _T ) with respect to the empirical loss L _T (C _T ) using uniform stability. A learning algorithm is stable (Bousquet and Elisseeff 2002) if its output does not change significantly under a small modification of the learning sample. We consider the following definition of uniform stability meaning that the replacement of one example must lead to a variation bounded in O(1/N _T ) in terms of infinite norm.

Definition 6

(Jin et al. 2009; Bousquet and Elisseeff 2002)

A learning algorithm has a uniform stability in $\frac{\kappa}{N_{T}}$, where κ is a positive constant, if

$$\forall(T,z), \forall i,\quad\displaystyle\sup_{z_1,z_2} \big|V(C_T,z_1,z_2)-V(C_{T^{i,z}},z_1,z_2)\big|\leq \frac{\kappa}{N_T}, $$

where T ^i,z is the new set obtained by replacing z _i ∈T by a new example z.

To prove that GESL _V has the property of uniform stability, we need the following lemma and the k-Lipschitz property of V.

Lemma 1

Let F _T and $F_{T^{i,z}}$ be the functions to optimize, C _T and $C_{T^{i,z}}$ their corresponding minimizers, and β the regularization parameter used in GESL _V . Let $\varDelta C=(C_{T}-C_{T^{i,z}})$. For any t∈[0,1]:

$$\|C_T\|^2_{\mathcal{F}}-\|C_T -t\varDelta C\|^2_{\mathcal{F}}+\| C_{T^{i,z}}\|^2_{\mathcal{F}}-\|C_{T^{i,z}} +t\varDelta C\|^2_{\mathcal {F}} \leq\frac{(2N_T+N_L)t2k}{\beta N_TN_L}\|\varDelta C\|_{\mathcal{F}}. $$

Proof

See Appendix A.1. □

We can now prove the stability of GESL _V .

Theorem 3

(Stability of GESL _V )

Let N _T and N _L be respectively the number of training examples and landmark points. Assuming that N _L =αN _T , α∈[0,1], and that the loss function used in GESL _V is k-Lipschitz, then GESL _V has a uniform stability in $\frac{\kappa }{N_{T}}$, where $\kappa= \frac{2(2+\alpha)k^{2}}{\beta\alpha}$.

Proof

Using t=1/2 on the left-hand side of Lemma 1, we get

$$\|C_T\|^2_{\mathcal{F}}-\bigg\|C_T -\frac{1}{2}\varDelta C\bigg\| ^2_{\mathcal{F}} +\|C_{T^{i,z}}\|^2_{\mathcal{F}}-\bigg\|C_{T^{i,z}} +\frac{1}{2}\varDelta C\bigg\|^2_{\mathcal{F}}=\frac{1}{2}\|\varDelta C\|^2_{\mathcal{F}}. $$

Then, applying Lemma 1, we get

$$\frac{1}{2}\|\varDelta C\|^2_{\mathcal{F}}\leq\frac{(2N_T+N_L)k}{\beta N_TN_L}\| \varDelta C\|_{\mathcal{F}} \quad\Rightarrow\quad\|\varDelta C\|_{\mathcal {F}}\leq\frac{2(2N_T+N_L)k}{\beta N_TN_L}. $$

Now, from the k-Lipschitz property of V, we have for any z,z′

$$\big|V\bigl(C_T,z,z'\bigr)-V\bigl(C_{T^{i,z}},z,z'\bigr)\big|\leq k\|\varDelta C\|_{\mathcal{F}} \leq\frac{2(2N_T+N_L)k^2}{\beta N_TN_L}. $$

Replacing N _L by αN _T completes the proof. □

Now, using the property of stability, we can derive our generalization bound over L(C _T ). This is done by using the McDiarmid inequality (McDiarmid 1989).

Theorem 4

(McDiarmid 1989)

Let X ₁,…,X _n be n independent random variables taking values in X and let Z=f(X ₁,…,X _n ). If for each 1≤i≤n, there exists a constant c _i such that

To derive our bound on L(C _T ), we just need to replace Z by D _T in Theorem 4 and to bound E _T [D _T ] and $|D_{T}-D_{T^{i,z}}|$, which is shown by the following lemmas.

Lemma 2

For any learning method of estimation error D _T and satisfying a uniform stability in $\frac{\kappa}{N_{T}}$, we have $\mathbf{E}_{T}[D_{T}]\leq\frac{2\kappa}{N_{T}}$.

Proof

See Appendix A.2. □

Lemma 3

For any edit cost matrix learned by GESL _V using N _T training examples and N _L landmarks, and any loss function V satisfying (σ,m)-admissibility, we have the following bound:

$$\forall i,1\leq i\leq N_T,\forall z,\quad|D_T - D_{T^{i,z}}|\leq\frac {2\kappa}{N_T} + \frac{(2N_T+N_L)(2\sigma+m)}{N_TN_L}. $$

Proof

See Appendix A.3. □

We are now able to derive our generalization bound over L(C _T ).

Theorem 5

(Generalization bound for GESL _V )

Let T be a sample of N _T randomly selected training examples and let C _T be the edit cost matrix learned by GESL _V with stability $\frac{\kappa}{N_{T}}$. Assuming that V(C _T ,z,z′) is k-Lipschitz and (σ,m)-admissible, and using N _L =αN _T landmark points, with probability 1−δ, we have the following bound for L(C _T ):

$$L(C_T)\leq L_T(C_T) + 2\frac{\kappa}{N_T}+ \biggl(2\kappa+\frac{2+\alpha }{\alpha} (2\sigma+m ) \biggr)\sqrt{\frac{\ln(2/\delta)}{2N_T}} $$

with $\kappa=\frac{2(2+\alpha)k^{2}}{\alpha\beta}$.

Proof

Recall that D _T =L(C _T )−L _T (C _T ) and N _L =αN _T . From Lemma 3, we get

$$|D_T - D_{T^{i,z}}|\leq\sup_{T,z'} |D_T - D_{T^{i,z'}}|\leq\frac {2\kappa+B}{N_T} \quad\textrm{with}\ B=\frac{(2+\alpha)}{\alpha}(2\sigma+m). $$

Then by applying the McDiarmid inequality, we have

$$ \mathrm{Pr}\bigl[\big|D_T -\mathbf{E}_T[D_T]\big| \geq\epsilon\bigr]\leq2\exp\biggl(-\frac{2\epsilon^2}{\sum _{i=1}^{N_T}\frac{(2\kappa+B)^2}{N_T^2}} \biggr)\leq2\exp\biggl(- \frac{2\epsilon^2}{\frac{(2\kappa+B)^2}{N_T}} \biggr). $$

(3)

By fixing ${\delta}=2\exp(-\frac{2\epsilon^{2}}{({2\kappa+B})^{2}/N_{T}} )$, we get $\epsilon=({2\kappa+B})\sqrt{\frac{\ln(2/\delta)}{2N_{T}}}$. Finally, from (3), Lemma 2 and the definition of D _T , we have with probability at least 1−δ:

$$ D_T < \mathbf{E}_T[D_T]+\epsilon \quad\Rightarrow\quad L(C_T) < L_T(C_T) + 2 \frac{\kappa}{N_T}+(2\kappa+B)\sqrt{\frac{\ln(2/\delta)}{2N_T}}. $$

 □

5.2 Generalization bound for the hinge loss

Theorem 5 holds for any loss function V(C _T ,z,z′) that is k-Lipschitz and (σ,m)-admissible with respect to C _T . Let us now rewrite this bound when V is the hinge loss-based function used in GESL _HL . We first have to prove that V is k-Lipschitz (Lemma 4) and (σ,m)-admissible (Lemma 6). Then, we derive the generalization bound for GESL _HL .

In order to fulfill the k-Lipschitz and (σ,m)-admissibility properties, we suppose every string length bounded by a constant W>0. Since the Levenshtein script contains at most $\operatorname {max}(|x_{1}|,|x_{2}|)$ operations, this implies that for any string pair,

$$\big\|\#(x_1,x_2)\big\|_{\mathcal{F}}=\sqrt{\sum_{l,c}\# _{l,c}(x_1,x_2)^2}\leq\sqrt{ \biggl(\sum_{l,c}\#_{l,c}(x_1,x_2) \biggr)^2} \leq W. $$

We will also denote $\|\#(x_{1},x_{2})\|_{\mathcal{F}}\leq W$ by $\|\# (z_{1},z_{2})\|_{\mathcal{F}}\leq W$ for the sake of convenience when using labeled examples.

Lemma 4

The function V used in GESL _HL is k-Lipschitz with k=W.

Proof

See Appendix A.4. □

We will now prove that V is (σ,m)-admissible for any optimal solution C _T learned by GESL _HL (Lemma 6). To be able to do this, we must show that the norm of C _T is bounded (Lemma 5).

Lemma 5

Let (C _T ,B ₁,B ₂) an optimal solution learned by GESL _HL from a training sample T, and let B _γ =max(η _γ ,−log(1/2)). Then $\|C_{T}\|_{\mathcal{F}}\leq\sqrt{\frac{B_{\gamma}}{\beta}}$.

Proof

See Appendix A.5. □

Lemma 6

For any optimal solution (C _T ,B ₁,B ₂), the function V used in GESL _HL is (σ,m)-admissible with $\sigma=\frac{\sqrt {\frac{B_{\gamma}}{\beta}}W+3B_{\gamma}}{2}$ and $m=\sqrt{\frac{B_{\gamma}}{\beta}}W$, with B _γ =max(η _γ ,−log(1/2)).

Proof

Let C _T be an optimal solution learned by GESL _HL from a training sample T and let z ₁,z ₂,z ₃,z ₄ be four labeled examples. We study two cases:

• 1. If $\ell_{z_{1}}\ell_{z_{2}}=\ell_{z_{3}}\ell_{z_{4}}$, whatever the labels of each examples are, using the 1-Lipschitz property of the hinge loss, the B ₁ (when $\ell_{z_{1}}\ell_{z_{2}}=\ell_{z_{3}}\ell _{z_{4}}=-1$) or B ₂ ($\ell_{z_{1}}\ell_{z_{2}}=\ell_{z_{3}}\ell_{z_{4}}=1$) values cancel out (in a similar way as in Lemma 4) and thus:

  

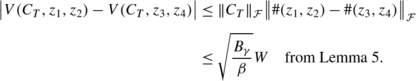
• 2. Otherwise, if $\ell_{z_{1}}\ell_{z_{2}}\neq\ell_{z_{3}}\ell_{z_{4}}$, note that |B ₁+B ₂|=η _γ +2B ₂≤3B _γ and $|\ell _{z_{1}}\ell_{z_{2}}-\ell_{z_{3}}\ell_{z_{4}}|=2$. Hence, whatever the labels of the examples compatible with this case, by using the 1-Lipschitz property of hinge loss and application of the triangular inequality, we get

  

Then, by choosing $\sigma=\frac{\sqrt{\frac{B_{\gamma}}{\beta}}W+3B_{\gamma}}{2}$ and $m=\sqrt{\frac{B_{\gamma}}{\beta}}W$, we have that V is (σ,m)-admis.  □

We can now give the convergence bound for GESL _HL .

Theorem 6

(Generalization bound for GESL _HL )

Let T be a sample of N _T randomly selected training examples and let C _T be the edit cost matrix learned by GESL _HL with stability $\frac{\kappa}{N_{T}}$ using N _L =αN _T landmark points. With probability 1−δ, we have the following bound for L(C _T ):

$$L(C_T)\leq L_T(C_T) + 2\frac{\kappa}{N_T}+ \biggl(2\kappa+\frac{2+\alpha}{\alpha} \biggl(\frac{2W}{\sqrt{\beta B_\gamma}}+3 \biggr)B_\gamma \biggr)\sqrt {\frac{\ln(2/\delta)}{2N_T}} $$

with $\kappa=\frac{2(2+\alpha)W^{2}}{\alpha\beta}$ and $B_{\gamma}=\operatorname{max}(\eta_{\gamma},-\log(1/2))$.

Proof

It directly follows from Theorem 5, Lemma 4 and Lemma 6 by noting that $2\sigma+m= (\frac{2W}{\sqrt{\beta B_{\gamma}}}+3 )B_{\gamma}$. □

5.3 Discussion

The generalization bounds presented in Theorems 5 and 6 outline three important features of our approach. To begin with, it has a convergence in $O(\sqrt{1/N_{T}})$, which is classical with the notion of uniform stability. Second, this rate of convergence is independent of the alphabet size, which means that our method should scale well to problems with large alphabets. We will see in Sect. 6 that it is the case in practice. Finally, thanks to the relation between the optimized criterion and the definition of (ϵ,γ,τ)-goodness that we established earlier, these bounds also ensure the goodness in generalization of the learned similarity function. Therefore, they guarantee that the similarity will induce low-error classifiers for the classification task at hand.

Note that to derive Theorem 6, we assumed the size of the strings was bounded by a constant W. Even though this is not a strong restriction, it would be interesting to get rid of this assumption and derive a bound that is independent of W. This is possible when the marginal distribution of P over the set of strings follows a generative model ensuring that the probability of a string decreases exponentially fast with its length. In this case, we can use the fact that very long strings have a very small probability to occur. Then with high probability, we can bound the maximum string length in a sample and remove W from the generalization bound. Indeed, one can show that for any string stochastic language p defined by a probabilistic automaton (Denis et al. 2006) or a stochastic context-free grammar (Etessami and Yannakakis 2009), there exist some constants U>0 and 0<ρ<1 such that the sum of the probabilities of strings of length at least k is bounded:

$$ \sum_{x, |x|>=k} p(x)< U \rho^k. $$

(4)

To take into account this result in our framework, we need an estimation of the length of all the examples used to derive the generalization bound, that is, a sample of N _T examples with two additional examples z and z′. For any sample of N _T +2 strings identically and independently drawn from p, we can bound the length of any string x of this sample. With a confidence greater than 1−δ/2(N _T +2), we have:

$$|x|<\frac{\log(U2(N_T+2)/\delta)}{\log(1/\rho)}, $$

by fixing δ/2(N _T +2)=Uρ ^k.

Applying this result to every string of the sample, we get that with probability at least 1−δ/2, any sample of N _T +2 elements has only strings of size at most $\frac{\log(U2(N_{T}+2)/\delta)}{\log(1/\rho)}$. Then, by using Theorem 6 with a confidence δ/2 and replacing W by $\frac{\log(2(N_{T}+2)U/\delta)}{\log(1/\rho)}$, we obtain the following bound.

Theorem 7

Let T be a sample of N _T randomly selected training examples drawn from a stochastic language p and let C _T be the edit costs learned by GESL _HL with stability $\frac{\kappa}{N_{T}}$ using N _L =αN _T landmark points. Then there exists constants U>0 and 0<ρ<1 such that with probability at least 1−δ, we have:

$$L(C_T)\leq L_T(C_T) + 2\frac{\kappa}{N_T}+ \biggl(2\kappa+\frac{2+\alpha}{\alpha} \biggl(\frac{2\log(2(N_T+2)U/\delta)}{\sqrt{\beta B_\gamma}\log(1/\rho )}+3 \biggr)B_\gamma \biggr)\sqrt{\frac{\ln(4/\delta)}{2N_T}} $$

with $\kappa=\frac{2(2+\alpha)\log^{2}(2(N_{T}+2)U/\delta)}{\alpha\beta\log ^{2}(1/\rho) }$ and $B_{\gamma}=\operatorname{max}(\eta_{\gamma},-\log(1/2))$.

Finally, let us conclude this section by discussing the adaptation of the entire theoretical analysis to tree edit similarity learning. The generalization bound for GESL _V (Theorem 5) holds since the arguments used in Sect. 5.1 are not specific to strings. Regarding the bound for GESL _HL (Theorem 6), we used the assumption that the length of the strings is bounded by a constant W. This can be easily adapted to trees: if we assume that the size of each tree (in its number of nodes) is bounded by W, Theorem 6 also holds. Finally, the arguments for deriving a bound independent of the constant W hold for trees since the property (4) is also valid for rational stochastic tree languages (Denis et al. 2008).

6 Experimental results

In this section, we provide an experimental evaluation of GESL _HL .⁴ We compare three edit similarity functions: (i) K _G , learned by GESL _HL ,⁵ (ii) the Levenshtein distance e _L , which constitutes the baseline, and (iii) an edit similarity function p _e learned with an EM-like algorithm (Oncina and Sebban 2006).⁶ Linear classifiers are learned from these similarity functions using the linear program (1) presented in Sect. 2.1. We show results on two datasets: English and French words (Sect. 6.1) and handwritten digits (Sect. 6.2).

6.1 English and French words

The task is to learn a model to classify words as either English or French. We use the 2,000 top words lists from Wiktionary.⁷

6.1.1 Convergence rate

We first assess the convergence rate of the two considered edit cost learning methods (i and iii). We keep aside 600 words as a validation set to tune the parameters, using 5-fold cross-validation and selecting the value offering the best classification accuracy. We build bootstrap samples T from the remaining 2,000 words to learn the edit costs (5 runs for each size N _T ), as well as 600 words to train the separator α and 400 words to test its performance.

Figure 4 shows the accuracy and sparsity results of each method with respect to N _T , averaged over 5 runs. We see that K _G leads to more accurate classifiers than e _L and p _e for N _T >20. The difference is statistically significant: the Student’s t-test yields a p-value <0.01. At the same time, K _G requires 3 to 4 times less reasonable points, thus increasing classification speed by just as much. The exact figures are as follows: e _L achieves 69.55 % accuracy with a model size of 197, p _e achieves at best 74.80 % with a model size of 155, and K _G achieves at best 78.65 % with a model size of only 45. This clearly indicates that GESL _HL leads to a better similarity than (ii) and (iii). Moreover, the convergence rate of GESL _HL is very fast, considering that (26+1)²=729 costs must be learned: it needs very few examples (about 20) to outperform the Levenshtein distance, and less than 500 examples to reach convergence. This provides experimental evidence that our method scales well with the size of the alphabet, as suggested by the generalization bound derived in Sect. 5.2. On the other hand, (iii) seems to suffer from the large number of costs to estimate: it needs a lot more examples to outperform Levenshtein (about 200) and convergence seems to be only reached at 1,000.

Fig. 4

Learning the costs: accuracy and sparsity results with respect to N _T (English and French words dataset)

6.1.2 Pairing strategy and influence of α

Here, we compare the two pairing strategies (random pairing and Levenshtein pairing) presented in Sect. 4.3 as well as the influence of α (the proportion of landmarks associated with each training example). Figure 5 shows the accuracy and sparsity results obtained for N _T =1500 with respect to α and the pairing strategies.⁸ The accuracy for e _L and p _e is carried over from Fig. 4 for comparison (model sizes for e _L and p _e , which are not shown for scale reasons, are 197 and 152 respectively).

Fig. 5

Pairing strategies: accuracy and sparsity results with respect to α (English and French words dataset)

These results are very informative. Regardless of the pairing strategy, K _G outperforms e _L and p _e even when making use of a very small proportion of the available pairs (1 %), which tremendously reduce the complexity of the similarity learning phase. Random pairing gives better results than Levenshtein pairing for α≤0.4. When α≥0.6, this trend is reversed. This means that for a small proportion of pairs, we learn better from pairing random landmarks than from pairing landmarks that are already good representatives of the training examples. On the other hand, when the proportion increases, Levenshtein pairing allows us to avoid pairing examples with the “worst” landmarks: best results are obtained with Levenshtein pairing and α=0.8.

6.1.3 Learning the separator

We now assess the performance of the three edit similarities with respect to the number of examples d _l used to learn the separator α. For K _G and p _e , we use the edit cost matrix that performed best in Sect. 6.1.1. Taking our set of 2,000 words, we keep aside 400 examples to test the models and build bootstrap samples from the remaining 1,600 words to learn α. Figure 6 shows the accuracy and sparsity results of each method with respect to d _l , averaged over 5 runs. Again, K _G outperforms e _L and p _e for every size d _l (the difference is statistically significant with a p-value <0.01 using a Student’s t-test) while always leading to (up to 5 times) sparser models. Moreover, the size of the models induced by K _G stabilizes for d _l ≥400 while the accuracy still increases. This is not the case for the models induced by e _L and p _e , whose size keeps growing. To sum up, the best similarity learned by GESL _HL outperforms the best similarity learned with the method of Oncina and Sebban (2006), which had been proven to outperform other state-of-the-art methods.

Fig. 6

Learning the separator: accuracy and sparsity results with respect to d _l (English and French words dataset)

6.1.4 Reasonable points analysis

Finally, one may wonder what kind of words are selected as reasonable points in the models. The intuition is that they should be some sort of “discriminative prototypes” the classifier is based on. To investigate this, using K _G and a training set of 1,200 examples, we learned a classifier α with a high value of λ to enforce a very sparse model, thus making the analysis easier. The set of 11 reasonable points automatically selected during the learning process is shown in Table 1. Our interpretation of why these particular words were chosen is that this small set actually carries a lot of discriminative patterns. Table 2 shows some of these patterns (extracted by hand from the reasonable points of Table 1) along with their number of occurrences in each class over the entire dataset. For example, words ending with ly correspond to English words, while those ending with que characterize French words. Note that Table 1 also reflects the fact that English words are shorter on average (6.99) than French words (8.26) in the dataset, but the English (resp. French) reasonable points are significantly shorter (resp. longer) than the average (mean of 5.00 and 10.83 resp.), which allows better discrimination. Note that we generated other sets of reasonable points from several training sets and observed the same patterns.

Table 1 Example of a set of 11 reasonable points

Table 2 Some discriminative patterns extracted from the reasonable points of Table 1 ($\hat{\ }$: start of word, $: end of word, ?: 0 or 1 occurrence of preceding letter)

6.2 Handwritten digits

We use the NIST Special Database 3 of the National Institute of Standards and Technology, describing a set of 10,000 handwritten characters in the form of 128×128 bitmap images. Each instance is represented as a string of Freeman codes (Freeman 1974) following the contour (starting from the top left pixel of the digit), as shown in Fig. 7. Classifying digits using this string representation and edit similarities yields close-to-perfect accuracy, even in the multi-class setting (Oncina and Sebban 2006; Bellet et al. 2010, 2011a). In order to make the comparison between the edit similarities (i–iii) easier, we evaluate them on the binary task of discriminating between even and odd digits. This task is harder due to extreme within-class variability: each class is in fact a “meta-class” containing instances of 5 basic classes of digits. Therefore, every example is highly dissimilar to about 80 % of the examples of its own class (e.g., 1’s are dissimilar to 5’s and 0’s are dissimilar to 4’s, although they belong to the same class).

Fig. 7

Three digits (0, 1, 8) and their respective string representation

6.2.1 Convergence rate

Once again, we assess the convergence of the cost learning methods (i and iii). We keep aside 2,000 words as a validation set to tune the parameters (using 5-fold cross-validation and selecting the value offering the best classification accuracy) as well as 2,000 words for testing the models. We build bootstrap samples T from the remaining 6,000 words to learn the edit costs (5 runs for each size N _T ), as well as 400 words to train the separator α.

Figure 8 shows the accuracy and sparsity results of each method with respect to N _T , averaged over 5 runs. First of all, we notice that the Levenshtein distance e _L performs nicely on this task (95.19 % with a model size of 70) and that p _e is never able to match e _L ’s accuracy level (94.94 % at best with a model size of 78). In our opinion, this poor performance comes from the fact that p _e does not take advantage of negative pairs. In a context of extreme within-class variability, moving closer examples of the same class without making sure that examples of different class are kept far from each others yields an underperforming similarity. On the other hand, our method shows the same general behavior on this task as on the previous task. Indeed, convergence is fast despite the richness of the two classes (only 100 examples to match Levenshtein’s accuracy and about 1,000 to reach convergence). Moreover, K _G achieves significantly better performance (95.63 % at best with a model size of 57) than both e _L (p-value <0.05 for N _T ≥250 using a Student’s t-test) and p _e (p-value <0.01 for N _T >20).

Fig. 8

Learning the costs: accuracy and sparsity results with respect to N _T (handwritten digits dataset)

6.2.2 Pairing strategy and influence of α

Figure 9 shows the accuracy and sparsity results obtained for N _T =2000 with respect to α and the pairing strategies. The performance for e _L and p _e is carried over from Fig. 8 for comparison. Results are very different from those obtained on the previous dataset. Here, K _G with random pairing is always outperformed by both e _L and p _e . On the other hand, K _G with Levenshtein pairing performs better than every other approaches for 0.05≤α≤0.4. This behavior can be explained by the meta-class structure of the dataset. When using random pairing, many training examples are paired with landmarks of the same class but yet very different (for instance, a 1 paired with a 5, or a 0 paired with a 4), and trying to “move them closer” is a fruitless effort. On the other hand, we know that the Levenshtein distance is an appropriate measure to discriminate between handwritten digits (Oncina and Sebban 2006; Bellet et al. 2010, 2011a). Therefore, when using Levenshtein pairing with α≤0.2, the problematic situation explained above rarely occurs. When α>0.2, since each meta-class is made out of 5 basic classes in even proportions, more and more examples are paired with “wrong” landmarks and the performance drops dramatically.

Fig. 9

Pairing strategies: accuracy and sparsity results with respect to α (handwritten digits dataset)

This result yields a valuable conclusion: similarity learning should not always focus on optimizing over all possible pairs (although it is often the case in the literature), since it may lead to poor classification performance. In some situations, such as the presence of high within-class variability, it may be a better strategy to improve the similarity according to a few carefully selected pairs.

6.2.3 Reasonable points analysis

To provide an insight into what kind of digits are selected as reasonable points, we follow the same procedure as in Sect. 6.1.4 using a training set of 2,000 examples. We end up with a set of 13 reasonable points. The corresponding digit contours are drawn in Fig. 10, allowing a graphical interpretation of why these particular examples were chosen. Note that this set is representative of a general tendency: we experimented with several training sets and obtained similar results. The most striking thing about this set is that 7’s are over-represented (4 out of the 6 reasonable points of the odd class). This is explained by the fact that 7’s (i) account for 1’s and 9’s (their contour is very similar), which also gives a reason for the absence of 1’s and 9’s in the set, and (ii) are not similar to any even digits. The same kind of reasoning applies to 6’s (the lower part of 6’s is shared by 0’s and 8’s, but not by any odd number) and 3’s (lower part is the same as 5’s). We can also notice the presence of 4’s: they have a contour mostly made of straight lines, which is unique in the even class. There is also a 2 which contour is somewhat similar to a 1. Lastly, another explanation for having several occurrences of the same digit may be to account for variations of size (the two 4’s), shape or orientations (the three 6’s).

Fig. 10

Example of a set of 13 reasonable points

7 Conclusion and perspectives

In this work, we proposed a novel loss minimization-based approach to the problem of learning edit similarities from data, called GESL. Our formulation is based on the notion of (ϵ,γ,τ)-goodness, which gives conditions for a similarity function to allow one to learn well without metric or PSD requirement. As opposed to most state-of-the-art approaches, GESL is not based on a costly iterative procedure but on solving an efficient convex program, and can accommodate both positive and negative training pairs. Furthermore, it is also a suitable way to learn tree edit similarities.

We provided a theoretical analysis of GESL, which holds for a large class of loss functions. A generalization bound in $O(\sqrt {1/N_{T}})$ was derived using the notion of uniform stability. This bound is (i) related to the goodness of the resulting similarity, which gives guarantees that the similarity will induce accurate classifiers for the task at hand, and (ii) independent from the size of the alphabet, making GESL suitable for problems involving large vocabularies.

We conducted experiments on two string datasets that shows that GESL has fast convergence and that the learned similarities perform very well in practice, inducing more accurate and sparser models than other (standard or learned) edit similarities. We also studied two pairing strategies and observed that Levenshtein pairing is more stable to high within-class variability, and that considering all possible pairs is not necessarily a good approach.

An interesting perspective is to assess the relevance of similarities learned with GESL when used in k-Nearest Neighbors classifiers. Indeed, when using Levenshtein pairing, GESL’s objective is somewhat related to the k-NN prediction rule. This intuition is confirmed by preliminary results using a 1-NN classifier (Fig. 11), where K _G outperforms e _L and p _e on both datasets. These first results open the door to a further theoretical analysis and might lead to k-NN generalization guarantees for GESL.

Fig. 11

1-Nearest Neighbor accuracy results for both datasets

Another promising avenue of research is to learn (ϵ,γ,τ)-good similarities for data made of vectors, in particular Mahalanobis distances, which have attracted a lot of interest in the similarity learning community. The theory of (ϵ,γ,τ)-goodness offers a new objective to optimize the transformation matrix (based on an average of similarity scores) and does not require the similarity function to be a valid metric, while satisfying this requirement is the bottleneck in many Mahalanobis distance learning approaches. This opens the door to efficient learning of (ϵ,γ,τ)-good “Mahalanobis-like” similarities.

Appendix

1.1 A.1 Proof of Lemma 1

Lemma 1

Let F _T and $F_{T^{i,z}}$ be the functions to optimize, C _T and $C_{T^{i,z}}$ their corresponding minimizers, and β the regularization parameter. Let $\varDelta C=(C_{T}-C_{T^{i,z}})$. For any t∈[0,1]:

$$\|C_T\|^2_{\mathcal{F}}-\|C_T -t\varDelta C\|^2_{\mathcal{F}}+\| C_{T^{i,z}}\|^2_{\mathcal{F}}-\|C_{T^{i,z}} +t\varDelta C\|^2_{\mathcal {F}} \leq\frac{(2N_T+N_L)t2k}{\beta N_TN_L}\|\varDelta C\|_{\mathcal{F}}. $$

Proof

The first steps of this proof are similar to the proof of Lemma 20 in Bousquet and Elisseeff (2002) which we recall for the sake of completeness. Recall that any convex function g verifies

$$\forall x,y, \forall t\in[0,1],\quad g\bigl(x+t(y-x)\bigr)-g(x)\leq t\bigl(g(y)-g(x)\bigr). $$

$L_{T^{i,z}}(\cdot)$ is convex and thus for any t∈[0,1],

$$ L_{T^{i,z}}(C_T-t\varDelta C) -L_{T^{i,z}}(C_T) \leq t\bigl(L_{{T^{i,z}}}(C_{T^{i,z}})- L_{T^{i,z}}(C_T) \bigr). $$

(5)

Switching the role of C _T and $C_{T^{i,z}}$, we get:

$$ L_{T^{i,z}}(C_{T^{i,z}}+t\varDelta C) -L_{T^{i,z}}(C_{T^{i,z}}) \leq t\bigl( L_{T^{i,z}}(C_T)-L_{{T^{i,z}}}(C_{T^{i,z}}) \bigr). $$

(6)

Summing up inequalities (5) and (6) yields

(7)

Now, since C _T and $C_{T^{i,z}}$ are minimizers of F _T and $F_{T^{i,z}}$ respectively, we have:

(8)

(9)

By summing up (8) and (9) we get:

By summing this last inequality with (7), we obtain

Let $B=L_{T}(C_{T}-t\varDelta C)-L_{T^{i,z}}(C_{T}-t\varDelta C)-(L_{T}(C_{T})-L_{T^{i,z}}(C_{T}))$, we have then

(10)

We now derive a bound for B. In the following, $z'_{k_{j}}\in T$ denotes the jth landmark associated to z _k ∈T such that $f_{land_{T}}(z_{k},z'_{k_{j}})=1$ in T, and $z'^{i}_{k_{j}}\in T^{i,z}$ the jth landmark associated to $z^{i}_{k}\in T^{i,z}$ such that $f_{land_{T^{i,z}}}(z^{i}_{k},z'^{i}_{k_{j}})=1$ in T ^i,z.

This inequality is obtained by developing the sum of the first two terms of the second line. The examples z _i in T and z in T ^i,z have N _L landmarks defined by $f_{land_{T}}$ and $f_{land_{T^{i,z}}}$ respectively.

Note that the samples of N _T −1 elements T∖{z _i } and T ^i,z∖{z} are the same and thus $z_{k}=z^{i}_{k}$ when k≠i. Therefore, for any z _k ∈T∖{z _i }, the sets of landmarks $L_{T}^{z_{k}}=\{z'_{k_{j}}\in T|f_{land_{T}}(z_{k},z'_{k_{j}})=1\}$ and $L_{T^{i,z}}^{z_{k}}=\{z'^{i}_{k_{j}}\in T^{i,z}|f_{land_{T^{i,z}}}(z_{k},z'^{i}_{k_{j}})=1\}$ differ on at most two elements, say $z_{i},z'_{k_{j_{2}}}\in L_{T}^{z_{k}}\backslash L_{T^{i,z}}^{z_{k}}$ and $z,z'^{i}_{k_{j_{1}}}\in L_{T^{i,z}}^{z_{k}}\backslash L_{T}^{z_{k}}$. Thus, some terms cancel out and we have:

The first two lines of the absolute value can be bounded by:

$$\bigl(2(N_T-1)+N_L\bigr)\sup_{\substack{z_1,z_2\in T\\z_3,z_4\in T^{i,z}}} \big|V(C_T-t\varDelta C,z_1,z_2)-V(C_T-t\varDelta C,z_3,z_4)\big|. $$

The same analysis can be done for the part in parentheses of the last line of the absolute value and we can take the pair of examples in T and in T ^i,z maximizing the whole absolute value to obtain the next inequality:

We continue by applying a reordering of the terms and the triangular inequality to get the next result:

We then use twice the k-Lipschitz property of V which leads to:

Then, by applying this bound on B from inequality (10), we get the lemma. □

1.2 A.2 Proof of Lemma 2

Lemma 2

For any learning method of estimation error D _T and satisfying a uniform stability in $\frac{\kappa}{N_{T}}$, we have $\mathbf{E}_{T}[D_{T}]\leq\frac{2\kappa}{N_{T}}$.

Proof

First recall that for any T,z,z′, by hypothesis of uniform stability we have:

$$\big|V(C_T,z,z') -V(C_{T^{k,z}},z,z')\big|\leq \sup_{z_1,z_2} \big|V(C_T,z_1,z_2) -V(C_{T^{k,z}},z_1,z_2)\big|\leq \frac{\kappa}{N_T}. $$

Now, we can derive a bound for E _T [D _T ].

The last inequality is obtained by applying the hypothesis of uniform stability to the second part of the sum. Now, since T,z and z′ are i.i.d. from distribution P, we do not change the expected value by replacing one point with another and thus:

$$\mathbf{E}_{\substack{T,z,z'}}\bigl[\big|V\bigl(C_T,z,z'\bigr)- V\bigl(C_T,z_k,z'\bigr)\big |\bigr]=\mathbf{E}_{\substack{T,z,z'}}\bigl[\big|V\bigl(C_T^{z,k},z_k,z'\bigr)- V\bigl(C_{T},z_k,z'\bigr)\big|\bigr]. $$

Then we get the result by applying this trick twice on the first element of the sum:

 □

1.3 A.3 Proof of Lemma 3

Lemma 3

For any edit cost matrix learned by GESL _V using N _T training examples and N _L landmarks, and any loss function V satisfying (σ,m)-admissibility, we have the following bound:

$$\forall i,1\leq i\leq N_T, \forall z,\quad|D_T - D_{T^{i,z}}|\leq\frac {2\kappa}{N_T} + \frac{(2N_T+N_L)(2\sigma+m)}{N_TN_L}. $$

Proof

First, we derive a bound on $|D_{T} - D_{T^{i,z}}|$.

Now, proving Lemma 3 boils down to bounding the last term above. Using arguments similar to those used in the second part of the proof of Lemma 1, we get

$$\big|L_{T^{i,z}}(C_{T^{i,z}})-L_{T}(C_{T^{i,z}})\big|\leq\frac {(2N_T+N_L)}{N_TN_L}\sup_{\substack{z_1,z_2\in T\\z_3,z_4\in T^{i,z}}}\big|V(C_{T^{i,z}},z_1,z_2) - V(C_{T^{i,z}},z_3,z_4)\big|. $$

Now by the (σ,m)-admissibility of V, we have that:

$$ \big|V(C_{T^{i,z}},z_1,z_2) - V(C_{T^{i,z}},z_3,z_4)\big| \leq\sigma|l_1l_2-l_3l_4|+m \leq2\sigma+m, $$

since whatever the labels, |l ₁ l ₂−l ₃ l ₄|≤2. This leads us to the desired result. □

1.4 A.4 Proof of Lemma 4

Lemma 4

The function V used in GESL _HL is k-Lipschitz with k=W.

Proof

We need to bound |V(C,z,z′)−V(C′,z,z′)| which implies to consider two cases: when z and z′ have the same labels and when they have different labels. We consider here the first case, the second one can be easily derived from the first one (B ₁ playing the same role as B ₂).

The second line is obtained by the 1-Lipschitz property of the hinge loss:

$$\big|[X]_+-[Y]_+\big|\leq|X-Y|. $$

The fourth one comes from the Cauchy-Schwartz inequality:

$$\Bigg|\sum_{i=1}^n\sum _{j=1}^m x_{ij} y_{ij}\Bigg| \leq\|x \|_{\mathcal{F}}\|y\|_{\mathcal{F}}. $$

Finally, since by hypothesis $\|\#(z,z')\|_{\mathcal{F}}\leq W$, the lemma holds. □

1.5 A.5 Lemma 5

Lemma 5

Let (C _T ,B ₁,B ₂) an optimal solution learned by GESL _HL from a training sample T, and let B _γ =max(η _γ ,−log(1/2)). Then $\|C_{T}\|_{\mathcal{F}}\leq\sqrt{\frac{B_{\gamma}}{\beta}}$.

Proof

Since (C _T ,B ₁,B ₂) is an optimal solution, the value reached by the objective function is lower than the one obtained with (0,B _γ ,0), where 0 denotes the null matrix:

For the last inequality, note that regardless of the possible labels of z _k and $z'_{k_{j}}$, $V(\boldsymbol{0},z_{k},z'_{k_{j}})$ is bounded either by B _γ or 0.

Since $\sum_{k=1}^{N_{T}}\frac{1}{N_{T}}\sum_{j=1}^{N_{L}}\frac{1}{N_{L}} V(C,z_{k},z'_{k_{j}})\geq0$, we get $\beta\|C_{T}\|^{2}_{\mathcal{F}}\leq B_{\gamma}$. □