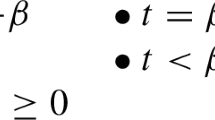Abstract
Contingency and accident are two important notions in philosophy and philosophical logic. Their meanings are so close that they are mixed up sometimes, in both daily life and academic research. This indicates that it is necessary to study them in a unified framework. However, there has been no logical research on them together. In this paper, we propose a language of a bimodal logic with these two concepts, investigate its model-theoretical properties such as expressivity and frame definability. We axiomatize this logic over various classes of frames, whose completeness proofs are shown with the help of a crucial schema. The interactions between contingency and accident can sharpen our understanding of both notions. Then we extend the logic to a dynamic case: public announcements. By finding the required reduction axioms, we obtain a complete axiomatization, which gives us a good application to Moore sentences.
Similar content being viewed by others
References
Ariew, R., & Garber, D. (Eds., and trans.). G. W. Leibniz: Philosophical essays. Indianapolis: Hackett Publishing Company, 1989.
Aristotle. (1941). De Interpretatione (On Interpretation). In McKeon, R. (Ed.) The Basic Works of Aristotle. New York: Random House.
Brogan, A. (1967). Aristotle’s logic of statements about contingency. Mind, 76 (301), 49–61.
Cresswell, M. (1988). Necessity and contingency. Studia Logica, 47, 145–149.
Fan, J. Strong non-contingency: on the modal logics of an operator expressively weaker than necessity. Accepted by Notre Dame Journal of Formal Logic.
Fan, J. (2015). Logics of essence and accident. arXiv:1506.01872 unpublished manuscript.
Fan, J., Wang, Y., van Ditmarsch, H. (2014). Almost necessary. In Advances in modal logic, (Vol. 10 pp. 178–196).
Fan, J., Wang, Y., van Ditmarsch, H. (2015). Contingency and knowing whether. The Review of Symbolic Logic, 8(1), 75–107.
Fine, K. (2017). Ignorance of ignorance. Synthese, 1–15.
Fitch, F.B. (1963). A logical analysis of some value concepts. The Journal of Symbolic Logic, 28(2), 135–142.
French, R., & Humberstone, L. (2009). Partial confirmation of a conjecture on the boxdot translation in modal logic. The Australasian Journal of Logic, 7, 56–61.
Gilbert, D.R., & Venturi, G. (2016). Reflexive-insensitive modal logics. The Review of Symbolic Logic, 9(1), 167–180.
Heinemann, F.H. (1948). Truths of reason and truths of fact. The Philosophical Review, 57(5), 458–480.
Hintikka, J. (1962). Knowledge and belief. Ithaca: Cornell University Press.
Holliday, W., & Icard, T. (2010). Moorean phenomena in epistemic logic. In Beklemishev, L., Goranko, V., Shehtman, V. (Eds.) Advances in Modal Logic 8 (pp. 178–199): College Publications.
Humberstone, L. (1995). The logic of non-contingency. Notre Dame Journal of Formal Logic, 36(2), 214–229.
Kuhn, S. (1995). Minimal non-contingency logic. Notre Dame Journal of Formal Logic, 36(2), 230–234.
Marcos, J. (2005). Logics of essence and accident. Bulletin of the Section of Logic, 34(1), 43–56.
Montgomery, H., & Routley, R. (1966). Contingency and non-contingency bases for normal modal logics. Logique et Analyse, 9, 318–328.
Moore, G.E. (1942). A reply to my critics. In Schilpp, P.A. (Ed.) The Philosophy of G.E. Moore. The Library of Living Philosophers (volume 4) (pp. 535–677). Evanston: Northwestern University.
Small, C.G. (2001). Reflections on Gödel’s ontological argument. In Deppert, W., & Rahnfeld, M. (Eds.) Klarheit in Religionsdingen: Aktuelle Beitrage zur Religionsphilosophië, volume Band III of Grundlagenprobleme unserer Zeit, pages 109–144. Leipziger Universitätsverlag.
Steinsvold, C. (2008). Completeness for various logics of essence and accident. Bulletin of the Section of Logic, 37(2), 93–101.
Steinsvold, C. (2008). A note on logics of ignorance and borders. Notre Dame Journal of Formal Logic, 49(4), 385–392.
Steinsvold, C. (2011). The boxdot conjecture and the language of essence and accident. Australasian Journal of Logic, 10, 18–35.
van Benthem, J. (2004). What one may come to know. Analysis, 64(2), 95–105.
van Benthem, J. (2011). Logical dynamics of information and interaction. Cambridge: Cambridge University Press.
van Ditmarsch, H., & Fan, J. (2016). Propositional quantification in logics of contingency. Journal of Applied Non-Classical Logics, 26(1), 81–102.
van Ditmarsch, H., van der Hoek, W., Kooi, B. (2007). Dynamic epistemic logic, volume 337 of synthese library. Berlin: Springer.
Zolin, E. (1999). Completeness and definability in the logic of noncontingency. Notre Dame Journal of Formal Logic, 40(4), 533–547.
Acknowledgements
This research is supported by the project 17CZX053 of National Social Science Fundation of China. We would like to thank Reinhard Muskens and an anonymous referee for careful reading of earlier versions and making insightful comments, which help improve the paper substantially.
Author information
Authors and Affiliations
Corresponding author
Appendix: The Proofs of Propositions 28 and 29
Appendix: The Proofs of Propositions 28 and 29
To show Proposition 28, we show that in K4∇∙, (1) Δϕ→ΔnΔmϕ (i.e. Δϕ→Δn+mϕ), (2) Δϕ→Δl∘kϕ, (3) Δϕ→∘jΔiϕ, (4) Δϕ→∘h∘gϕ (i.e. Δϕ→∘h+gϕ) are all provable, where \(1\leq n,m,l,k,j,i,h,g\in \mathbb {N}\). The proofs are shown by induction on n to g. The base case of each item follows from Proposition 27. We only need to consider the inductive step.
For (1), by induction hypothesis, we have ⊩Δϕ→Δn+mϕ, to show that ⊩Δϕ→Δn+m+ 1ϕ. For this, we have the following proof sequences:
For (2), by induction hypothesis, we have ⊩Δϕ→Δl∘kϕ. We need to show that ⊩Δϕ→Δl+ 1∘kϕ and ⊩Δϕ→Δl∘k+ 1ϕ. For this, we have the following proof sequences:
For (3), by induction hypothesis, we have ⊩Δϕ→∘jΔiϕ. We need to show that ⊩Δϕ→∘j+ 1Δiϕ and ⊩Δϕ→∘jΔi+ 1ϕ. Note that ∘ (ϕ→ψ) ∧∘ϕ ∧ ϕ→∘ ψ (denoted (⋆)) is a validity, thus also a theorem of K4∇∙. Then we have the following proof sequences:
For (4), by induction hypothesis, we have ⊩Δϕ→∘h+gϕ, to show that ⊩Δϕ→∘h+g+ 1ϕ. For this, we have the following proof sequences:
This concludes the proof of Proposition 28.
To show Proposition 29, we show that in K4∇∙, (1) ⊩Δϕ→(Δl∘k)mϕ and (2) ⊩Δϕ→(∘jΔi)nϕ, where \(1\leq n,m,l,k,j,i\in \mathbb {N}\). We proceed by induction on m and n, respectively.
-
Base step, i.e. m = 1 and n = 1. This follows directly from Proposition 28.
-
Inductive step. Assume by induction hypothesis that the proposition holds for the cases m and n, respectively. We need to show the cases m + 1 and n + 1, respectively, i.e., ⊩Δϕ→(Δl∘k)m+ 1ϕ and ⊩Δϕ→(∘jΔi)n+ 1ϕ.
The proofs are as follows.
$$\begin{array}{lll} (i)&{\Delta}^{l + 1}{\circ}^{k}{\phi}{\to}({\Delta}^{l}{\circ}^{k})^{m}{\Delta}^{l}{\circ}^{k}{\phi}&\text{IH}\\ (ii)&{\Delta}{\phi}{\to} {\Delta}^{l + 1}{\circ}^{k}{\phi}&\text{Proposition~28}\\ (iii)&{\Delta}{\phi}{\to}({\Delta}^{l}{\circ}^{k})^{m + 1}{\phi}&(i)(ii) \end{array} $$$$\begin{array}{lll} (i)&{\Delta}{\circ}^{j}{\Delta}^{i}{\phi}{\to}({\circ}^{j}{\Delta}^{i})^{n}{\circ}^{j}{\Delta}^{i}{\phi}&\text{IH}\\ (ii)&{\Delta}^{i + 1}{\phi}{\to} {\Delta}{\circ}^{j}{\Delta}^{i}{\phi}&\text{Proposition~28}\\ (iii)&{\Delta}{\phi}{\to}{\Delta}^{i + 1}{\phi}&\text{Proposition~28}\\ (iv)&{\Delta}{\phi}{\to}({\circ}^{j}{\Delta}^{i})^{n + 1}{\phi}&(i)-(iii) \end{array} $$
Rights and permissions
About this article
Cite this article
Fan, J. Bimodal Logics with Contingency and Accident. J Philos Logic 48, 425–445 (2019). https://doi.org/10.1007/s10992-018-9470-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10992-018-9470-5