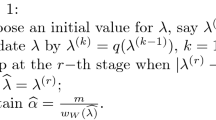Flexible two-piece distributions for right censored survival data

Abstract

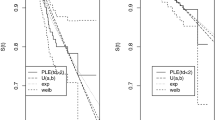
An important complexity in censored data is that only partial information on the variables of interest is observed. In recent years, a large family of asymmetric distributions and maximum likelihood estimation for the parameters in that family has been studied, in the complete data case. In this paper, we exploit the appealing family of quantile-based asymmetric distributions to obtain flexible distributions for modelling right censored survival data. The flexible distributions can be generated using a variety of symmetric distributions and monotonic link functions. The interesting feature of this family is that the location parameter coincides with an index-parameter quantile of the distribution. This family is also suitable to characterize different shapes of the hazard function (constant, increasing, decreasing, bathtub and upside-down bathtub or unimodal shapes). Statistical inference is done for the whole family of distributions. The parameter estimation is carried out by optimizing a non-differentiable likelihood function. The asymptotic properties of the estimators are established. The finite-sample performance of the proposed method and the impact of censorship are investigated via simulations. Finally, the methodology is illustrated on two real data examples (times to weaning in breast-fed data and German Breast Cancer data).

Appendices

Appendix A Proofs of Theorems 2.1 and 2.2 (basic properties)

1.1 A.1 Proof of Theorem 2.1

For $t< \eta$, we can write

$$\begin{aligned} F_{\alpha }(t;\eta ,\phi )&=\int _{-\infty }^{t}f_{\alpha }(s;\eta ,\phi )ds \\&=\frac{2\alpha (1-\alpha )}{\phi } \int _{0}^{t} g'(s)f_{0}\left\{ (1-\alpha )\left( \frac{g(\eta )-g(s)}{\phi }\right) \right\} ds, \qquad \text{ since }~ s> 0\\&= 2\alpha F_{0}\left\{ (1-\alpha )\left( \frac{g(t)-g(\eta )}{\phi }\right) \right\} , \end{aligned}$$

where we used a change of variable $z=(1-\alpha )\left( \frac{g(\eta )-g(s)}{\phi }\right) .$ Similarly, for $t\ge \eta$, we have

$$\begin{aligned} F_{\alpha }(t;\eta , \phi )&=\int _{-\infty }^{t}f_{\alpha }(s;\eta , \phi )ds = \int _{0}^{\eta }f_{\alpha }(s;\eta , \phi )ds + \int _{\eta }^{t}f_{\alpha }(s;\eta , \phi )ds \\&=\frac{2\alpha (1-\alpha )}{\phi } \bigg [\int _{0}^{\eta } g'(s)f_{0}\left\{ (1-\alpha )\left( \frac{g(\eta )-g(s)}{\phi }\right) \right\} ds\\&\quad +\int _{\eta }^{t}g'(s)f_{0}\left\{ \alpha \left( \frac{g(s)-g(\eta )}{\phi }\right) \right\} ds \bigg ] \\&=2\alpha -1+2(1-\alpha )F_{0}\left\{ \alpha \left( \frac{g(t)-g(\eta )}{\phi }\right) \right\} ,~ \text {through a change of variable}\\ z&=\alpha \left( \frac{g(s)-g(\eta )}{\phi }\right) \end{aligned}$$

Finally, the quantile function of T for any quantile order $\uptau \in (0,1)$ given in (2.3) is the inverse of $F_{\alpha }(t;\eta , \phi )$. $\square$

1.2 A.2 Proof of Theorem 2.2

For the survival function given in Theorem 2.2 (i), we use that $S_{\alpha }(t)=P(T>t)=1-F_{\alpha }(T\le t)$. Considering this together with the property that $S_{0}(z)+S_{0}(-z)=1$, we can write for $t< \eta$

$$\begin{aligned} \begin{aligned} S_{\alpha }(t;\eta ,\phi )= 1-2\alpha S_{0}\left\{ (1-\alpha )\left( \frac{g(\eta )-g(t)}{\phi }\right) \right\} , \end{aligned} \end{aligned}$$

and for $t\ge \eta$, we have

$$\begin{aligned} \begin{aligned} S_{\alpha }(t;\eta , \phi )=2(1-\alpha )S_{0}\left\{ \alpha \left( \frac{g(t)-g(\eta )}{\phi }\right) \right\} . \end{aligned} \end{aligned}$$

Now, the hazard function for the random variable T is defined by the ratio of the probability density function and the corresponding survival function. Thus,

$$\begin{aligned} \begin{aligned} h_{\alpha }(t;\eta , \phi )&=\displaystyle \frac{f_{\alpha }(t;\eta , \phi )}{S_{\alpha }(t; \eta , \phi )} \\&=\displaystyle \frac{\alpha g'(t)}{\phi }\left\{ \begin{array}{ll} \displaystyle \frac{ 2(1-\alpha ) h_{0}\left[ (1-\alpha )\left( \frac{g(\eta )-g(t)}{\phi }\right) \right] S_{0}\left[ (1-\alpha )\left( \frac{g(\eta )-g(t)}{\phi }\right) \right] }{1-2\alpha S_{0}\left[ (1-\alpha )\left( \frac{g(\eta )-g(t)}{\phi }\right) \right] } &{} \text{ if }\, t<\eta \\ \displaystyle h_{0}\left[ \alpha \left( \frac{g(t)-g(\eta )}{\phi }\right) \right] &{}~ \text{ if }\, t\ge \eta , \end{array} \right. \end{aligned} \end{aligned}$$

where $h_{0}$ is the hazard rate function for the underlying distribution with density $f_{0}$. Finally, to prove Theorem 2.2 (iii) we start from the definition of the cumulative hazard function, and find

$$\begin{aligned} \begin{aligned} \varLambda _{\alpha }(t;\eta , \phi )&= \displaystyle \int _{0}^{t}h_{\alpha }(s)ds= -\ln S_{\alpha }(t;\eta , \phi )\\&= \displaystyle \left\{ \begin{array}{ll} \displaystyle -\ln \left\{ 1-2\alpha S_{0}\left[ (1-\alpha )\left( \frac{g(\eta )-g(t)}{\phi }\right) \right] \right\} &{} \text{ if }\, t<\eta \\ \displaystyle -\ln [2(1-\alpha )] + \varLambda _{0}\left[ \alpha \left( \frac{g(t)-g(\eta )}{\phi }\right) \right] &{}~ \text{ if }\, t\ge \eta , \end{array} \right. \end{aligned} \end{aligned}$$

where $\varLambda _{0}(.)$ is the cumulative hazard function associated with the density $f_{0}$. $\square$

Appendix B Proofs of Theorems 3.1 and 3.2

1.1 B.1 Proof of Theorem 3.1 (consistency)

Since the likelihood function is not differentiable with respect to $\eta$ at $\eta =y_{i}$ for all $i=1,\cdots , n$, the GQBA family does not satisfy the usual regularity conditions to prove the asymptotic properties of MLEs. Huber (1967) established the consistency and asymptotic normality of any sequence of estimators under nonstandard conditions. We here follow Huber’s method in the right censored data case. Since we assumed independent censoring with non-informative censoring mechanism, we do not have identifiability issues between survival and censoring time distributions. Let $(\varOmega , \mathcal {F}, \mathcal {P})$ be a probability space of $(Y, \varDelta )$ with $\varOmega = \mathbb {R}^{+}_{0}\times \{0,1\}$ and $\varvec{\varPsi }(\varvec{\theta };Y, \varDelta )$ be a vector of the score function on ${\varvec{\varTheta }}_{R}\times \varOmega$ given as

$$\begin{aligned} \begin{aligned} \varvec{\varPsi }(\varvec{\theta };Y, \varDelta )= \begin{bmatrix} \psi _{1}(\varvec{\theta };Y, \varDelta ) \\ \psi _{2}(\varvec{\theta };Y, \varDelta ) \\ \psi _{3}(\varvec{\theta };Y, \varDelta ) \end{bmatrix}&= \begin{bmatrix} \frac{1}{2}\bigg (\frac{\partial }{\partial \eta ^{{\varvec{-}}}}\ell (\varvec{\theta }; Y, \varDelta ) + \frac{\partial }{\partial \eta ^{+}}\ell (\varvec{\theta }; Y, \varDelta )\bigg )\\ \frac{\partial }{\partial \phi }\ell (\varvec{\theta };Y, \varDelta )\\ \frac{\partial }{\partial \alpha }\ell (\varvec{\theta }; Y, \varDelta ) \end{bmatrix}, \end{aligned} \end{aligned}$$

where $\frac{\partial }{\partial \eta ^{-}}\ell (\varvec{\theta }; Y, \varDelta )$ and $\frac{\partial }{\partial \eta ^{+}}\ell (\varvec{\theta }; Y, \varDelta )$ denote the left-hand and right-hand derivative with respect to $\eta$, respectively. The aim is to prove the convergence of any sequence ${\varvec{\widehat{\theta }}}_{n}$ such that

$$\begin{aligned} \frac{1}{n}\sum _{i=1}^{n}\varvec{\varPsi }( \widehat{\varvec{\theta }}_{n};Y_{i}, \varDelta _{i})\xrightarrow {\text {a.s}} \varvec{0}, \end{aligned}$$

converges almost surely to $\varvec{\theta }_{0}$. We want to give sufficient conditions for the assumptions that have been established in Theorem 2 of Huber (1967, pp. 224–225). Sufficient conditions such that Huber’s assumptions for the consistency of the estimator $\widehat{{\varvec{\theta }}}_{n}$ hold, are:

(H-1).:

For each fixed ${\varvec{\theta }}\in {\varvec{\varTheta }}_{R}, ~ {\varvec{\varPsi }}(\varvec{\theta };Y, \varDelta )$ is $\varOmega$-measurable and separable.

(H-3).:

The expected value $\lambda (\varvec{\theta })=\mathrm {E}_{Y, \varDelta }\big [\varvec{\varPsi }( \varvec{\theta };Y,\varDelta )\big ]$ exists for all ${\varvec{\theta }}\in {\varvec{\varTheta }}_{R}$, and has a unique zero at ${\varvec{\theta }}={\varvec{\theta }}_{0}$.

(H-2$^\prime$).:

As the neighbourhood $U_{\theta }$ of ${\varvec{\theta }}$ shrinks to $\{{\varvec{\theta }}_{0}\}$

$$\begin{aligned} \mathrm {E}_{Y, \varDelta }\big \{{u( \varvec{\theta }; Y, \varDelta )}\big \}\rightarrow \varvec{0}, \end{aligned}$$

where $u(\varvec{\theta }; Y, \varDelta )=\underset{\varvec{\theta }_{0}\in U_{\theta }}{\text {sup}}\Vert \varvec{\varPsi }(\varvec{\theta }_{0};Y, \varDelta )-\varvec{\varPsi }(\varvec{\theta }; Y, \varDelta )\Vert$, $\Vert \cdot \Vert$ denotes Euclidean norm.

We can prove (H-1) by imposing Assumption (B1), in that we have ${\varvec{\varTheta }}_{R}$ as a compact subset of the parameter space ${\varvec{\varTheta }}$. It is also well known that a compact space is totally bounded and complete. We also know that a compact space is separable (Van der Vaart 2000). Furthermore, the score function $\varvec{\varPsi }(\varvec{\theta };Y, \varDelta )$ is a function of ${\varvec{\theta }}$ in a compact space ${\varvec{\varTheta }}_{R}$, and it also depends on the random variables Y and $\varDelta$; hence separability is achieved here. Note that, $\varvec{\varPsi }(\varvec{\theta };Y, \varDelta )$ is a measurable function of $(Y, \varDelta )$ for each ${\varvec{\theta }}$ since it is established from a joint probability distribution defined on the measure space $(\varOmega , \mathcal {F}, \mathcal {P})$.

For the second assumption (H-3), we first need to check the identifiability of the parameters, i.e., for $\varvec{\theta }\ne \varvec{\theta }_{0}$, we need to ensure that $\ell (\varvec{\theta }; y, \delta )\ne \ell (\varvec{\theta }_{0};y, \delta )$. We have that $\exp \big (\ell (\varvec{\theta }_{0};y, \delta =1)\big )=f_{\alpha _{0}}(y; \varvec{\theta }_{0})$ and $\exp \big (\ell (\varvec{\theta }_{0};y, \delta =0)\big )=S_{\alpha _{0}}(y;\varvec{\theta }_{0})\equiv 1-F_{\alpha _{0}}(y;\varvec{\theta }_{0})$. In the complete data analysis, Gijbels et al. (2019a) proved the identifiability issue by comparing the mode value in $f_{\alpha }(y;\varvec{\theta })$ and $f_{\alpha _{0}}(y;\varvec{\theta }_{0})$. Consider $f_{\alpha }(y;\varvec{\theta })=f_{\alpha _{0}}(y;\varvec{\theta }_{0})$, which shows that both densities have the same mode $\eta =\eta _{0}$, since each distribution of GQBA family is unimodal at $\eta$. Moreover, $f_{\alpha }(y;\varvec{\theta })=f_{\alpha _{0}}(y;\varvec{\theta }_{0})$ implies $S_{\alpha }(y;\varvec{\theta })=S_{\alpha _{0}}(y;\varvec{\theta }_{0})$ and also $\alpha =F_{\alpha }(\eta )=F_{\alpha _{0}}(\eta _{0}))=\alpha _{0}$, which indicates that $\alpha =\alpha _{0}$. Therefore, $f_{\alpha }(\eta ; \varvec{\theta })=f_{\alpha _{0}}(\eta _{0}; \varvec{\theta }_{0})$ with $\eta =\eta _{0}$, and $\phi =\phi _{0}$. Hence, the identifiability of the parameters holds, i.e., $\varvec{\theta }=\varvec{\theta }_{0}$. In other words, $\varvec{\theta }\ne \varvec{\theta }_{0}\Rightarrow \ell (\varvec{\theta }; y, \delta )\ne \ell (\varvec{\theta }_{0};y, \delta )$.

The second condition (H-3) we first should check is the existence of the expected score function. Under Assumptions (B2)–(B5) we have a finite expected value of the score function as stated in Proposition 3.1; hence $\lambda (\varvec{\theta })$ exists for all $\varvec{\theta }\in {\varvec{\varTheta }}_{R}$, and has a unique zero at $\varvec{\theta }=\varvec{\theta }_{0}$.

For the last assumption (H-2$^\prime$) we know that $u(\varvec{\theta }; Y, \varDelta )$ is a continuous function in  $\varvec{\theta }$, and $\varvec{\theta }$ belongs to a compact set ${\varvec{\varTheta }}_{R}$. Hence, $u( \varvec{\theta }; Y, \varDelta )$ is bounded on ${\varvec{\varTheta }}_{R}$. It is also immediate from (H-2$^\prime$) that $\lambda ({\varvec{\theta }})$ is continuous. $\square$

1.2 B.2 Proof of Theorem 3.2 (asymptotic normality)

Similar to the consistency, we also established the asymptotic normality using the conditions of Theorem 3 in Huber (1967, pp. 226–227). Huber provides sufficient conditions which assure that every sequence of $\widehat{{\varvec{\theta }}}_{n}$ satisfying

$$\begin{aligned} \frac{1}{\sqrt{n}}\sum _{i=1}^{n}{\varvec{\varPsi }}( \widehat{{\varvec{\theta }}}_{n};Y_{i}, \varDelta _{i})\xrightarrow {P} {\varvec{0}}, \end{aligned}$$

is asymptotically normal.

• (N-1). For each fixed ${\varvec{\theta }}\in {\varvec{\varTheta }}_{R}, ~ {\varvec{\varPsi }}({\varvec{\theta }};Y, \varDelta )$ is $\varOmega$-measurable and separable.

• (N-2). There is a ${\varvec{\theta }}_{0}\in \mathring{{\varvec{\varTheta }}}_{R}$ such that $\lambda ({\varvec{\theta }}_{0})={\varvec{0}}$.

• (N-3). There are strictly positive numbers $a, b, c, d_{0}$ such that

  • (i) $\Vert \lambda ({\varvec{\theta }})\Vert \ge a\Vert {\varvec{\theta }}-{\varvec{\theta }}_{0}\Vert$            for  $\Vert {\varvec{\theta }}-{\varvec{\theta }}_{0}\Vert \le d_{0}$,

  • (ii) $\mathrm {E}_{Y, \varDelta }\big [u(Y,\varDelta , {\varvec{\theta }}, d)\big ]\le bd$        for  $\Vert {\varvec{\theta }}-{\varvec{\theta }}_{0}\Vert +d\le d_{0}$,       $d\ge 0$,

  • (iii) $\mathrm {E}_{Y, \varDelta }\big [u(Y,\varDelta , {\varvec{\theta }}, d)^2\big ]\le cd$       for  $\Vert {\varvec{\theta }}-{\varvec{\theta }}_{0}\Vert +d\le d_{0}$,       $d\ge 0$.

  Where we define $u(Y,\varDelta , {\varvec{\theta }}, d)=\underset{\Vert {\varvec{\theta }}-{\varvec{\theta }}_{0}\Vert \le d}{\text {sup}}\Vert {\varvec{\varPsi }}({\varvec{\theta }}; Y, \varDelta )-{\varvec{\varPsi }}({\varvec{\theta }}_{0}; Y, \varDelta )\Vert$ for ${\varvec{\theta }}_{0}\in \mathring{{\varvec{\varTheta }}}_{R}$.

• (N-4). The expectation $\mathrm {E}_{Y, \varDelta }\big [||{\varvec{\varPsi }}({\varvec{\theta }}_{0};Y, \varDelta )||^2\big ]$ is finite.

Note that the first assumption (N-1) is the same as (H-1) in the consistency part, and already proved in Sect. B.1. Furthermore, for the second assumption (N-2), we already proved that $\lambda ({\varvec{\theta }})$ exists for all ${\varvec{\theta }}\in {\varvec{\varTheta }}_{R}$ in Proposition 3.1, and has a unique zero at ${\varvec{\theta }}={\varvec{\theta }}_{0}$ in (H-3) of Huber (1967). Since $\mathring{{\varvec{\varTheta }}}_{R}$ is an interior of ${\varvec{\varTheta }}_{R}$ and the expectations are always taken with respect to the true distributions $F_{\alpha _{0}}(y;\eta _{0}, \phi _{0})$ and G(.), we find that $\lambda ({\varvec{\theta }}_{0})={\varvec{0}}$.

The last two assumptions (N-3) and (N-4) involve the existence of the Fisher information matrix. Condition (N-4) holds, i.e., $\mathrm {E}_{Y, \varDelta }\big [||{\varvec{\varPsi }}({\varvec{\theta }}_{0};Y, \varDelta )||^2\big ]<\infty$, since

$$\begin{aligned} \begin{aligned} \mathrm {E}_{Y, \varDelta }\big [||{\varvec{\varPsi }}({\varvec{\theta }}_{0};Y, \varDelta )||^2\big ]&=\mathrm {E}_{Y, \varDelta }\big \{\big [{\varvec{\varPsi }}({\varvec{\theta }}_{0};Y, \varDelta )\big ]\big [{\varvec{\varPsi }}({\varvec{\theta }}_{0};Y, \varDelta )\big ]^{\scriptscriptstyle T}\big \}\\&=\text {Trace}[{\varvec{\mathcal {I}}}({\varvec{\theta }}_{0})]<\infty . \end{aligned} \end{aligned}$$

To prove (N-3), a Taylor expansion for $\lambda ({\varvec{\theta }})$ at the point ${\varvec{\theta }}_{0}$ has been used in Gijbels et al. (2019a). The interesting expression in this sense is that since $\lambda ({\varvec{\theta }})$ is continuously differentiable in any neighbourhood of ${\varvec{\theta }}_{0}$, and hence

$$\begin{aligned} \lambda ({\varvec{\theta }}) =\lambda ({\varvec{\theta }}_{0}) -{\varvec{\mathcal {I}}}({\varvec{\theta }}_{0}) ({\varvec{\theta }}-{\varvec{\theta }}_{0})+o\big (\Vert {\varvec{\theta }}-{\varvec{\theta }}_{0}\Vert \big ). \end{aligned}$$

For further details, see the reference above. $\square$