Introduction

The term spatial ecological networks appeared initially in Europe as part of nature conservation policy and is broadly defined as a network composed of ecological components, e.g. core areas, ecological corridors, and buffer zones (Jongman et al. 2004; McHugh and Thompson 2011). Greenways can be viewed as networks designed and managed for ecological, recreational, historical, aesthetic and cultural purposes. Such networks are mainly related to human needs, however, they can in some cases also assume the role of corridors for wildlife species, even though the vegetation may not be natural or present. Both concepts can be combined into a single structure, frequently called green infrastructure (Fumagalli and Toccolini 2012; Ignatieva et al. 2010), but to date no viable spatial ecological modelling tools have been successfully developed that can represent multiple uses or spatial distribution patterns.

Green infrastructure is broadly defined as a network of multifunctional ecosystems made of natural, semi-natural and artificial features, such as green spaces, water bodies, rivers and others. By connecting previously isolated habitats, increasing the vegetation cover, and contributing to ecosystem resilience, green infrastructures also improves the quality and quantity of ecosystem services and functions, that contributes to ecosystem and public health (Tzoulas et al. 2007). Various studies support this argument and have reported the services and functions provided by the natural components that are directly or indirectly beneficial to ecosystems, wildlife species and humans; functions such as air filtering, micro-climate regulation, noise reduction, rainwater drainage and sewage treatment (Bolund and Hunhammar 1999); heat island effect reduction, psychological well-being, longevity and levels of physical activity (Tzoulas et al. 2007); cultural, historical, aesthetic and recreational functions (Chiesura 2004); and biodiversity conservation and enhancement (Liu et al. 2014).

A key characteristic of effective spatial ecological networks, or in the design of appropriate green infrastructure, is landscape connectivity together with the concept of priority corridors. Landscape connectivity is broadly defined as ‘the degree to which the landscape facilitates or impedes movement among resource patches’ (Taylor et al. 1993). It facilitates the movement of organisms, genetic interchange and other ecological flows that are critical for the viability and survival of species and for the conservation of biodiversity in general (Crooks and Sanjayan 2006). This definition can be broken down into two complementary components: ‘structural connectivity’ and ‘functional connectivity’ (Saura and Torné 2009). Structural connectivity is a landscape-specific component and refers to the spatial arrangement of a physical structure that involves different elements such as suitable habitat continuity, distance between patches, length and extent of gaps, or network properties (Saura and Torné 2009). Various indices have been proposed to quantify the structural connectivity: e.g. mesh size, fractal dimension, network connectivity and circuitry (Forman 1995). Functional connectivity is both landscape and species-specific (Meiklejohn et al. 2009) and reflects the behavioral responses of a given species to a landscape structure. This behavioral component is influenced by various factors, including species habitat requirements, its tolerance to disturbed habitats and degree of specialization, the scale at which it moves within the landscape, or its response to predators and competitors (Bennett 2003).

For the purpose of connectivity analyses, landscapes are typically mapped as resistance surfaces, which are grids of raster cells with varying values depending on habitat qualities, movement barriers or dispersal routes. These grids, derived from graph theory, are represented as graphs, which are mapped networks in which raster cells are substituted by nodes connected by edges to their neighbors (McRae 2008). Many methods and related indices have been derived from these theoretic networks, such as the probability of connectivity index or the least-cost model (Etherington and Penelope Holland 2003; Saura and Rubio 2010). The least-cost model has increasingly become a popular method to assess connectivity and many studies have proved its usefulness (Richard and Armstrong 2010; Etherington and Penelope Holland 2003). Nevertheless, the fact that this method assumes that species’ movement is restricted to a single-optimal path has been an underlining limitation (McRae and Beier 2007).

The circuit model, a novel and less popular model associating graph and electronic circuit theories, has overcome this limitation (McRae and Beier 2007). This model relies on the same basic concepts as graph-theoretic models but differs in the fact that circuits are defined as ‘networks comprised of a set of nodes connected by resistors, instead of edges in graph models’ (McRae 2008). Using resistors connected to nodes is analogous to creating circuits and allows the computation of the effective resistance that reflect additional contributions from multiple paths (McRae 2008). Circuit models are thus able to identify alternative routes and to highlight pinch points (critical habitat connections) needing closer attention, as well as pointing out sections of the paths that belong to broadly suitable habitats (McRae 2008). Circuit models are also able to define priority corridors. However, these are difficult to discern on circuit maps, whilst least-cost models display them more clearly. In view of their respective constraints, McRae (2008) suggest circuits and least-cost models should not be considered as alternative methods but rather complementary approaches that can be applied in tandem to provide a more concrete assessment of landscape connectivity. Circuit models have mainly been used at regional scales using coarse spatial resolutions (Pelletier et al. 2014). Recently, they have also been applied at a finer city scale (Braaker 2014).

In Europe and North America, the median level of urbanization is expected to increase to 82% by 2050, compared to 74% in 2014 according to the United Nations (2014). As of today, Belgium is one of the most highly urbanized countries in this region, with 98% of its population in urban areas (United Nations 2014). In such urbanized environments, which belong to the most fragmented landscapes (Braaker 2012), the preservation and improvement of ecological networks supporting biodiversity, ecological processes, and ecosystem services is important for nature conservation and human well-being (Tzoulas et al. 2007). This study focuses on the City of Liège, the third most populated city of Belgium (Ville de Liège 2013). The two focal species involved in this study are humans and natterjack toads (Bufo calamita, syn. Epidalea calamita), an endangered species occurring in the city. Both species were also chosen to potentially highlight the twofold role of ecological networks in anthropogenic landscapes.

The aim of this study was therefore to present a novel methodological approach to assess and model connectivity for both species in the city, to identify potential priority corridors and to provide an initial guideline for urban planning and biodiversity conservation. The objectives were as follows: (1) to develop predictive connectivity models for two focal species based on least-cost and circuit models (2), to identify priority corridors, assess their connectivity and highlight critical connections within them, and (3) to provide recommendations to improve landscape connectivity for both species.

Materials and methods

Study framework

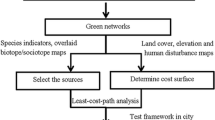
In this study, resistance surfaces, least-cost models and circuit models were integrated to identify the dispersal corridor network. This method involved (1) modelling resistance surfaces for human recreation and natterjack toads based on available data; (2) modelling hypothetical dispersal corridors from the resistance surface models using least-cost and circuit analyses with source sites for both species; and (3) identifying the priority corridors and assessing their connectivity by combining least-cost and circuit models.

Focal species

The level of connectivity in a landscape varies between environments, but most of all among species. Depending on the species, a landscape is thus perceived differently and may provide different levels of connectivity (Bennett 2003). From the literature, the following highlights the characteristics and behaviors of the focal species involved in this study.

Human walking for recreation, contributes to human health, safety and well-being. Walking is the most common physical activity practiced by adults and the most fundamental mode of transport in cities (Lindelöw et al. 2014; Owen et al. 2004). A study conducted in Montreal has shown that some people were willing to walk a maximal distance of approximately 3.5 km and average distances travelled by people walking to go to work and for recreation were 993 m and 860 m, respectively (Larsen et al. 2010).

In cities, the movement of pedestrians is mainly influenced by attractors and by the spatial configuration of the urban grid (Hillier et al. 1993). Their tolerance to detours is limited, but people may walk longer distances to access facilities or attractions (Broach 2015), such as sidewalks, aesthetic elements (e.g. attractive landscaping or buildings), natural features or walking destinations (Owen et al. 2004). Nevertheless, the importance of the factors influencing people’s route choice varies depending on the purpose of the walk. Those walking to work give more importance to the distance than to the destination (Weinstein Agrawal et al. 2008), whilst recreational walkers are more likely to choose a route based on its quality, paying more attention to the presence of sidewalks (Lee and Moudon 2006) and to visual aspects (e.g. parks, attractive buildings, etc.). Finally, all pedestrians perceive very steep terrain as a barrier (Broach 2015), but only those walking to work consider moderate slopes as barriers. By contrast, recreational walkers enjoy the views and greater exercise opportunities that such slopes offer (Lee and Moudon 2006). In this study, the key parameters included in the resistance models for human recreation were route quality, visual aspect, slope steepness and the presence of attractors such as parks, historic landmarks, greenspace and open urban space.

The natterjack toad (Bufo calamita, syn. Epidalea calamita) is a native species of western and central Europe. Since the twentieth century, this amphibian has suffered a major decline, due to habitat destruction, changes in its specialized biotopes and acidification of breeding sites by anthropogenic activities (Denton et al. 1997). The species is fully protected by the Convention on the Conservation of European Wildlife and Natural Habitats (European Council Directive 92/43/EEC 1992). In Wallonia, Belgium, the species is red listed (Jacob 2007) and benefits from protection under the Legislation for Nature Conservation, appendix IIa (2001).

The natterjack toad is mainly a nocturnal and crepuscular species that pursues invertebrate prey over open ground and short vegetation. Individuals are distributed in populations with a metapopulation structure. This population structure allows their persistence in fragmented environments via typical spatial and temporal dynamics of colonization-extinction (Denton et al. 1997; Jacob and Liste Rouge 2007). The natterjack toad is a pioneer heliophilous species that is found in various environments and can colonize recently or frequently disturbed environments. Its optimal habitats are open areas characterized by low and sparse vegetation cover (< 30 cm high), bare ground, light soils and shallow water bodies, e.g. river flood plains; marshes; sand dunes and heathlands (Denton et al. 1997; Jacob and Liste rouge. 2007). It can also be found in several habitats related to human activity: e.g. sand; clay or gravel pits; limestone quarries; vacant lots; industrial wastelands; slag heaps; agricultural land; artificial ponds; temporary puddles; railway drainage channels, roads or pathways’ and even in gardens or in house basements (Jacob and Liste rouge. 2007). They also benefit from anthropogenic activity in timber cutting and livestock grazing areas (Denton et al. 1997). In the northern part of its range i.e. Belgium and Great Britain, the species is also found in coastal sand dunes.

Adults and toadlets move through the landscape to reproduce, migrate, shelter and feed. Mature natterjack toads have been reported to be able to move one kilometer from their initial site (Miaud and Sanuy 2005). In specific cases, natterjack toads are able to travel longer distances e.g. from 1.2 to 2.6 km as reported in the Northern Rhineland (Miaud and Sanuy 2005) and about 3 km in Belgian Lorraine (Jacob and Liste Rouge 2007). Juveniles may migrate over several hundred meters (Jacob and Liste Rouge 2007). They move preferentially on bare ground (e.g. sandy soils, paths and roads), and subsequently where the vegetation is low and sparse, such as mowed grasslands (Clobert 2006) and avoid land cover with dense vegetation, e.g. forest and undergrowth, or cultivated soils (Clobert 2006). Slopes are not barriers for the species and can be considered as attractors in some particular cases (Rondel and Lemoine 2015). During the breeding season, they leave their shelter at night to reach water bodies where they reproduce (Jacob and Liste Rouge 2007). Males tend to show fidelity to their former breeding site, whereas females can change from one year to another (Clobert 2006). From this description, it can be argued that land cover types, location of breeding sites and occurrence sites are parameters to be included in resistance models for natterjack toads.

Focal area selection

Connectivity was modelled within two focal areas (A and B) located in Liège (50° 38′ N, 5° 34′ E), in the Meuse River valley, Eastern Belgium (Fig. 1). It has a greater urban area of 68.50 km2 and more than 617,000 citizens (Ville de Liège 2013). It contains residential and industrial areas, which become denser closer to the River Meuse. Focal area A was used to model human recreation and covered 8 km2 while focal area B was used for the natterjack toad and had an extent of 36 km2 (Table 1). The smaller extent of focal area A provided the opportunity to apply the analysis at a finer scale with more precision. Focal area B encompasses focal area A to identify potential corridors playing a twofold role, i.e., for human recreation and for natterjack toad movement (Table 1).

Fig. 1
figure 1

Focal areas and source sites (a for human recreation, b for natterjack toad); numbered polygons in the insets are the source sites for the connectivity analysis

Full size image
Table 1 Selected source sites for each species
Full size table

Data collection

The Biodiversity and Landscape Unit of Gembloux Agro-Bio Tech initially provided a NGI topographic polygon map at 10:000 scale and the PICC (Projet Informatique de Cartographie Continu) topographic lines and point layers. Layers representing land registry parcels, non-registered lands, public properties, open green space and slagheaps were also provided. A DTM raster (2014) was provided through a licence agreement between Liège University and the DGO4-SPW (Direction Générale Opérationelle du Service Public de Wallonie). A polygon layer of natterjack toad occurrence sites was provided by the studies department of Natagora.

Connectivity modelling

Four source sites were selected for both species within their respective focal areas. For human recreation, the chosen source sites were four important open green spaces identified as being disconnected from each other. The source sites for the natterjack toads were selected from the occurrence sites layer obtained from Natagora. Site 3 was located near the city centre and involved a potentially extinct population. The other three were located on the outskirts of the city and contained variable sized populations of natterjack toads. For the purpose of the study, distances between source sites were calculated from feature edges for both species using the Conefor Inputs extension for ArcGIS (Jeff Jenness Enterprises).

For human recreation, four parameters influencing human movements for recreation were identified: route quality, visual aspect, slope steepness and the presence of attractors. For the natterjack toad, three parameters were identified: land cover, presence of breeding sites and presence of occurrence sites. Presence of slagheaps, which represents a suitable habitat for the species, and building density were also identified as parameters influencing the species movement, even though they were not identified from the literature review.

For each focal species, the weight of each resistance model parameter was based on their relative importance identified from the literature and on assumptions by the authors. For human recreation, more weight was given to the route quality (50%) and visual aspect (30%), two factors reported to have a significant influence on the route choice of recreational walkers (Lee and Moudon 2006). Less weight was allocated to slope steepness (10%) and attractors (10%), based on the assumption that they have less influence on the route choice of walking for recreation. The parameter with the greatest weight for the natterjack toad was land cover (50%), a primary factor that influences the movement of the species (Jacob and Liste Rouge 2007), followed by the presence of potential breeding sites (15%) and occurrence sites (15%), based on the fact that males show fidelity to their former breeding site from where they attract females, thus influencing their movement and occurrence (Clobert 2006). Less importance was given to the presence of slagheaps (10%) as potential habitats for the species (Rondel and Lemoine 2015), and to building density (10%) based on the assumption that it could influence the habitat quality and movement of the species.

Resistance surfaces

Using the reclassified input layers and taking into account each parameter’s weight, resistance surface rasters were generated using the weighted overlay tool for both species. These initial resistance surface models were subsequently improved by adding physical barriers (e.g. fences, walls, hedgerows) from the PICC lines layers for both species. For human recreation, public properties and non-registered land layers were used to reclassify areas without public access as NoData i.e. they were not considered in any further analysis. Resistance surfaces were initially generated with a 1 m cell size. The resistance surface for natterjack toads was resampled to a 2 m cell size to reduce the number of cells analysed in the larger focal area B due to software limitations. Further detail on how the resistance values were determined can be found in the supplementary material.

Least-cost models

The tool Linkage Mapper 1.0 (McRae and Kavanagh 2011) generated least-cost models for both species. Resistance surfaces were used as cost surfaces together with the source site polygons and a file comprising calculated distances between source sites.

Circuit models

Circuit models were created using the Circuitscape software (McRae and Shah 2011). Resistance surfaces and source sites were converted into ASCII rasters via the Export to Circuitscape extension for ArcGIS (Jeff Jenness Enterprises). Circuit models for both species were generated using the pairwise mode in order to model the connectivity between all pairs of source sites.

Combined models

Pinchpoint Mapper 1.0, part of the Linkage Mapper toolkit, was used to create models combining least-cost and circuit methods. By constraining the current flow to the least-cost corridors identified, the combined method was able to highlight least-cost corridors and to assess the connectivity via the least-cost distance and least-cost path length metrics. Then, by running the Circuitscape software within the least-cost corridors, the tool assessed the connectivity via the effective resistance metric and mapped existing pinch points (critical connections) within least-cost corridors.

Scenario development for new green infrastructure

To assess how the connectivity models could be used to improve connectivity and to test their validity, the outputs were used to implement a fictional green infrastructure for human recreation project. The combined model for human recreation was used to identify areas that could be improved within the least-cost corridors. The inputs initially used to generate the connectivity models were modified while ensuring that the modifications would not result in unrealistic planning. The modifications were limited to modifying existing urban infrastructure such as adding trees along the least-cost corridors and converting land use/land cover (LULC) types where it was conceivable, e.g. converting bare ground into parks. Once the modifications were made, the improved inputs were used to generate a new resistance surface that was subsequently used to generate a combined model.

Results

The calculated straight-line distances between the source sites selected for human recreation ranged from 243 to 1830 m (Table 2). All were within the maximum acceptable distance for walking (3500 m) and only two of them exceeded the average walking distance for recreation (860 m). This means that people are able to walk between source sites if no significant detour is caused by the landscape structure. For the natterjack toad, the calculated straight-line distances ranged from 2761 to 7345 m (Table 2). All were greater than the approximate maximal dispersal range of 3000 m, with the exception of the calculated distance between source sites 2 and 3 (2761 m). This implies that, if the landscape structure permits it, the natterjack toad could travel between these two sites.

Table 2 Calculated straight-line distances between source site edges for each species
Full size table

Resistance surfaces

Figure 2 shows the resistance surface model maps of movement resistance for both species where the most suitable areas of the landscape are in green and the least suitable areas are red. For human recreation, resistance values range from 2 to 100 with a mean value of 35. Areas with the highest resistances are mainly related to the presence of physical barriers (e.g. walls, fences) or unsuitable land cover (e.g. brushwood, leafy forest with ligneous undergrowth). Some areas appear as darker orange because they are some distance from attractors or located on steep slopes. For natterjack toads, the resistance values also range from 2 to 100, but the mean value of 46 suggests that the overall resistance generated is higher than for human recreation. From Fig. 2, it can be observed that most of the resistance surface is composed of areas with moderate suitability (shown in yellow) for the species. Highly suitable areas are located on the resistance surface borders, due to the presence of occurrence sites, slagheaps and potential breeding sites surrounding the city.

Fig. 2
figure 2

a Landscape resistance for human recreation within focal area A, and b landscape resistance for natterjack toad within focal area B. Resistance values range from 2 (dark green) to 100 (red). Areas of the landscape with infinite resistance values (absolute barriers to movement) are transparent (Cell size: 1 m for A, and 2 m for B)

Full size image

Least-cost models

Least-cost models generate maps of cumulative cost that highlight least-cost corridors and least-cost paths between source sites. Cells with the lowest cumulative cost (yellow and orange) define the least-cost corridors, whilst the least cost paths (LCPs) are represented using black lines (Fig. 3). Cells with a high cumulative cost are shown in dark blue.

Fig. 3
figure 3

a Cumulative cost and identified Least Cost Paths between source sites for human recreation within focal area A, and b natterjack toad within focal area B (Cell size: 1 m for A, and 2 m for B)

Full size image

For human recreation, three least-cost corridors and their LCPs are identified on Fig. 3 and show that humans walking follow the sidewalk pattern and prefer streets without green elements when the distance saved is large. For the natterjack toad, four least-cost corridors and related LCPs were mapped within focal area B (Fig. 3). No LCP was identified between source sites 1 and 2 and between source sites 2 and 4. This can be explained by the fact that moving between these source sites via source site 3 is more cost-efficient for the species, since source sites are considered as areas of zero resistance. The combination of the LCPs identified for links A and C and the combination of the LCPs identified for links C and D thus endorse the role of least-cost paths between source sites 1 and 2 and 2 and 4, respectively. The short LCP length for link C (3051 m) reflects a better connectivity than for other links. This is mainly because the landscape structure between source sites 2 and 3 is less fragmented by urbanisation and generates fewer detours for the species than between other source sites. The fact that all LCP lengths exceed the approximate maximal dispersal range of the natterjack toad (3000 m) could explain the potential extinction of the species at source site 3. Nevertheless, the LCP length for link C (3051m) is just slightly over 3000m and represents the most cost-efficient path to connect source site 3 to a source site where the occurrence of the species is certified.

Circuit models

The outputs from the circuit models show the current density (Fig. 4). A high current density (yellow) indicates higher probability for species movement between source sites. The highest maximum current densities are observed where connectivity between source sites depends on single, narrow corridor segments. Contrary to the maps of cumulative cost, the maps of current density identify alternative routes connecting the source sites.

Fig. 4
figure 4

a Current density for human recreation within focal area A, and b natterjack toad within focal area B. Cells with high current density (yellow) indicate higher probabilities for moving between source sites. Cells with low current density (blue) show portions of the landscape contributing least to connectivity (e.g. habitat cul-de-sacs, corridors to nowhere)

Full size image

The linkages with the highest current densities (yellow) show similarity to the corridors identified by the least-cost model (Fig. 4). However, they do not always match the least-cost corridors. For example, the higher current density between source sites 1 and 2 follows a different route compared to the least-cost corridor identified between the same two source sites. This is because, contrary to least-cost models, circuit models simultaneously consider all possible linkages that can contribute to connectivity between source sites. Since the electrical circuit theory assumes that wider, multiple linkages connecting two source sites allow greater current flow than a narrow, single linkage, this explains why a higher current density is observed between source sites 1 and 2. For the natterjack toad, some linkages with high current density show similarity to the least-cost corridors identified (Figs. 3 and 4). Between source sites 2 and 3, no linkage was highlighted by a high current density because the landscape between those two source sites does not constrain the species to move on single, narrow routes.

Combined models

The combined models (Fig. 5) show the current density within the corridors identified in the least-cost models and provide values of effective resistance, a connectivity measure complementing LCP lengths. As for circuit model outputs, cells with high current density (yellow) show where species are more likely to move and cells with low current density (blue) show portions of the least-cost corridors that contribute less to connectivity. Only current density values within least-cost corridors are taken into account in combined models. In general, this means that smaller value ranges result, highlighting critical connections on a map more accurately.

Fig. 5
figure 5

a The current density for human recreation within the least-cost corridors identified for links A, B and C, and b the current density for the natterjack toad within the least-cost corridors identified for links A, B, C and D. Cells with high current density (yellow) indicate higher probabilities and cells with low current density (blue) show portions of the landscape contributing the least to connectivity

Full size image

Figure 5a shows current density within the least-cost corridors identified for links A, B and C for human recreation. A higher current density highlights pinch points, mainly related to the narrowness of sidewalks restricting current flow. Effective resistance values show that link B, between source sites 2 and 3, has a lower effective resistance, despite the shorter LCP length between source sites 1 and 2, which tends to indicate that the connectivity is better for link A. This is due to the fact that LCP lengths determine connectivity values by assuming that movement occurs on a single, optimal route, while the concept of effective resistance assumes that movement can occur over multiple routes and that wider routes allow greater movement flows.

The lower effective resistance for link B can be explained by the fact that it benefits from having a wider least-cost corridor and that it is connected to a larger number of alternative routes allowing a greater movement flow than link A. Link C has the highest effective resistance due to the larger distance between its related source sites and because the least-cost corridor connecting them consists of a small number of narrow routes. Figure 5b shows the effective resistance values for the natterjack toad. Link C has the best connectivity in terms of LCP length and effective resistance. The lower effective resistance for link C is explained by the reduced distance, less landscape structure fragmentation and the greater width of the least-cost corridor between source sites 2 and 3.

Scenario development around new green infrastructure

The outputs of the combined model for the green infrastructure project (Fig. 6) showed that modifying the inputs initially used to model and assess connectivity for human recreation has affected the shape of the least-cost corridors, previously identified (Fig. 5).

Fig. 6
figure 6

Current density for the green infrastructure project

Full size image

Comparing Figs. 5 and 6 showed that between source sites 1 and 2, the least-cost corridor has a lower current density in its northern section. This is because it was not possible to improve the northern section due to its narrowness, while the overall resistance of the southern section was decreased by green infrastructure improvements, allowing more current flow. Between source sites 2 and 3, the current density within the least-cost corridor does not show any obvious differences related to the green infrastructure improvements. Between source sites 3 and 4, the northern section of the least-cost corridor has disappeared and the two remaining sections have a higher current density. The green infrastructure improvements have created LCP lengths that are slightly longer than LCP lengths resulting from the combined model for human recreation. This can be explained by the fact that adding trees and creating parks has decreased the overall cost of travel and allows human walking for recreation to traverse longer distances for a lower cost within each least-cost corridor.

Comparing effective resistances between the two models shows that implementing green infrastructure has decreased the effective resistance for each least-cost corridor, with the exception of least-cost corridor C, where the effective resistance has increased. This increase is due to the loss of the northern section that was initially highlighted for human recreation (Fig. 6). Losing this section results in a loss of potential alternative paths to move between source sites 3 and 4. Regarding the two other least-cost corridors, the decrease of effective resistance indicates that a larger number of alternative paths contribute to connectivity.

Discussion

In heterogeneous and highly fragmented urban landscapes, the identification of corridors which have to be prioritized is essential to better design, preserve and improve green infrastructure. These networks of multifunctional ecosystems are undoubtedly crucial for human well-being and nature conservation since they support biodiversity, ecological processes and services in urbanized landscapes (Bolund and Hunhammar 1999; Chiesura 2004; Tzoulas et al. 2007).

The least-cost model proved to be an effective way to calculate distances and to identify the optimal routes between source sites. This method also provides an easily understandable assessment of connectivity via the least-cost path length metric, which is a much easier to interpret than accumulated-cost in terms of dispersal distance (Etherington and Penelope Holland 2003). Nevertheless, the study has demonstrated that the least-cost model also has constraints such as not considering all possible routes that could contribute to connectivity or providing connectivity assessments that are only related to a single, most cost-efficient route identified in a given landscape. These same limitations have been highlighted by McRae and Beier (2007).

For its part, the circuit theoretic model has shown that it was able to overcome the limitation of the least-cost model by simultaneously considering different suitable routes. This major advantage over the least-cost model was also mentioned by McRae and Beier (2007) and McRae (2008). In this study, the circuit model was also able to identify the critical connections that contribute most to network connectivity and the corridors with optimal connectivity. This study highlighted an additional limitation to the circuit theory approach in that the approach was only effective in heterogeneous urban landscapes, as illustrated by the results for the natterjack toad, for which only one optimal corridor (out of four identified by the least-cost model) was identified by the circuit model due to the presence of homogeneous areas around the city.

The combined model benefits from the advantages of both least-cost and circuit models. In our study, the outputs generated via the combined model showed the outlines of the optimal corridors identified by the least-cost models and highlighted the critical connections within them with more precision. It also provided an assessment of connectivity for each corridor via the least-cost path length metric. In addition, the combined model was able to compute the effective resistance for each least-cost corridor identified. This second connectivity metric complements the least-cost path length metric and reflects the contribution of alternative suitable corridors. Even though the combined model appears to be the ideal combination between least-cost and circuit models, it must be emphasized that the circuit models have to be processed in the first place in order to generate the combined model outputs, and to allow interpretation of the results.

The models and maps generated in this study present a first approximation of connectivity for both human use and a species of ecological significance, an integrative approach towards multiuse urban green space. The results indicate some of the challenges currently confronting the natterjack toad, particularly at one of the source sites selected. In the future, the outputs could be related to other datasets to provide more complete interpretations of ecological processes and phenomena. There are challenges related to the choice of scale at which these models are developed, a choice which is dependent on quality of LULC data available for the models but also a function of the species under consideration, its ecology and landscape. The combined models reflect a first approximation of the combined value of connectivity corridors, but need to be approached with an understanding of the underlying ecological considerations which reflect the species ecology and landscape under consideration.

There are a number of ways in which, once identified, priority areas and corridors can be managed to enhance biodiversity and connectivity. The current Aichi targets of the Biodiversity Convention inform a basis for authorities to develop plans aimed at conserving and enhancing urban biodiversity (Sirakaya et al. 2018), and these are linked to the United Nations Sustainable Development Goals, ensuring the sustainability of cities (Goal 11) and restoring ecosystem services and halting biodiversity loss (Goal 15) (United Nations 2015). Precisely what should go where is a question that has to be addressed at a number of scales, but decision making will be focused locally, but there are general approaches and methodologies which can be used as templates for developing prescriptions for action (e.g. Dover 2015). Using these tools, here we can help identify where investment in greenspace would result in most co-use value and by extension results in the highest increase in natural capital assets. This would be useful, for instance, in informing Urban masterplans but also local nature partnerships.

Conclusions

This study presents a methodological approach to assess and model connectivity for both species in the city in order to provide an initial guideline for urban planning and biodiversity conservation. Predictive connectivity models have been developed for two focal species based on least-cost and circuit models, priority corridors identified, connectivity assessed, critical connections within them highlighted, and recommendations provided to improve landscape connectivity for both species. The models used in the study have complementary approaches that can contribute to a more definitive assessment of connectivity for nature conservation and urban planning. The popular least-cost model is an efficient and reliable method to identify corridors for which maintenance and improvement have to be prioritized to establish ecological networks or to implement green infrastructure plans. The least-cost path lengths calculated by the least-cost models provide a convenient connectivity assessment that could explain the potential extinction of the natterjack toad at one of the source sites. The circuit model, despite the fact that it has not been widely used to date in connectivity studies, has proved to be a valuable method complementing the least-cost model by highlighting alternative corridors and critical connections that play an important role in landscape connectivity. The circuit model has also shown its ability to highlight priority corridors similar to the ones identified by the least-cost model in urban heterogeneous landscapes. However, it must be emphasized that it is not a suitable method to highlight priority corridors in homogeneous landscapes. The combined model is an effective way of highlighting critical connections within the priority corridors identified by the least-cost model. It allows the user to provide recommendations for the maintenance and improvement of existing corridors or for the creation of green infrastructure. This study can help nature conservation and guide urban planning decision making in maintaining ecological networks or designing appropriate green infrastructure. The multistep framework of this study allows other researchers to identify priority corridors in urban environments and quantify their connectivity.