Introduction

The quest to optimise the heat transfer performance of heat exchangers by researchers is a constant given the numerous research papers produced on this subject, be it via the optimisation of the conduit geometry or the introduction of a more performant working fluid. In the case of enhancement via an optimised conduit, the present research aims to expand on the existing research on the usage of swirling flow for the benefit of heat transfer, as past research typically studied the effects of having twisted tapes within a conduit. One such study by Manglik and Bergles [1] found that using twisted tapes in compact tube fin heat exchangers can be very beneficial for heat transfer performance and fouling reduction due to the thinner boundary layer that results in better overall heat transfer. Chang et al. [2] found that increasing the intensity of turbulence within a conduit by introducing multiple twisted tape inserts further improved the overall heat transfer when they compared the addition of 2 and 3 twisted tape inserts to compare against a single twisted tape insert. Bharadwaj et al. [3] studied the heat transfer performance of a spirally grooved tube, spirally grooved tube with clockwise twisted tape (parallel to groove direction) and the same tube with an anticlockwise twisted tape (opposing the groove direction). They found that grooves improved heat transfer performance for the laminar regime and cases with Reynolds number higher than 9000. They also noted a reduction in heat transfer performance over the standard non-grooved, non-finned case for Reynolds number between 2500 and 9000, which they regarded as an anomaly. Eiamsa-ard et al. [4] discussed the viability of using double twisted tapes where one forms a counter-swirl flow whilst the other forms a co-swirl flow. The authors found that the counter-swirl double tape insert performed the best, but they also noted that the enhancement index (heat transfer performance improvement relative to the increase in friction factor) improved when the twist ratio of the tape reduced. Kummitha et al. [5] discussed twisted tapes with helical protrusions placed along the tape at 90\(^\circ\) and 180\(^\circ\) twist angle intervals. As is the general trend with the discussed findings, the author found that heat transfer performance improved, and the pressure drop increased when the resulting turbulence increased with the addition of more helical inserts on the twisted tape.

Some notable works concerning swirl generators outside the twisted tape type design exist. Hay & West [6], Sparrow and Qhaboki [7], Yilmaz et al. [8] and Aydin et al. [9] studied the effect of swirling air on convective heat transfer by introducing a swirl generator at the inlet of the experimental conduit. They then calculated the local Nusselt number to understand the improvement in convective heat transfer as the swirl decayed in the air along the test chamber. The authors concluded that introducing a swirl generator increased the Nusselt number at the expense of pressure drop. Aydin et al. [9] further concluded a strong correlation with L/Dh (test section length to hydraulic diameter ratio) when concerning the heat transfer coefficient. The authors elaborated that this was due to the length of the test section determining the overall possible heat transfer improvement, with longer test sections yielding worse results due to the swirl’s decay. Bilen et al. [10] studied the swirl-inducing inlet where the swirl generator was long enough to ensure a good swirl was generated with minimum fluid disturbance due to the sudden redirection. The authors found that higher angle swirl generators produced better heat transfer performance across the outer walls of the test section. However, this also resulted in a higher pressure drop due to the increased friction factor. In essence, much research concerning the use of swirling flows for improving heat transfer performance studies decaying swirling flow of air. Given the limited scope of swirling flow-related research for use in hydraulic heat exchanger applications, there is a need to understand the potential improvement of heat transfer performance for small-scale heat exchanger applications as outlined by Manglik & Bergles [1] since such devices need to be compact, but not necessarily have the optimal heat transfer to pressure drop performance, as is the case in industrial applications. With that, this research will study the heat transfer performance of fin-induced swirling flows within an annular conduit with angled fins instead of the twisted tape approach.

The creation of colloidal suspensions via the dispersion of nanoparticles with high intrinsic thermal properties within a base fluid was done to enhance its thermophysical properties for heat transfer [11]. However, fluid viscosity was also found to be increased with increasing nanoparticle concentration. Eastman et al. [11] found that using nanopowders with high thermal conductivity increased the thermal conductivity of the base fluid it was added to substantially. They also found that the thermal conductivity achieved by the colloidal suspension depends on the volume fraction of the nanoparticles within the tested base fluid. Such fluids with enhanced thermal properties are known as nanofluids, a term coined by Choi & Eastman [12]. The addition of nanoparticles into base fluids for heat transfer applications has been apparent over the last couple of decades. It allows for smaller, more efficient heat exchangers with reduced energy consumption and operational costs [11]. One such application was demonstrated by Colangelo et al. [13], who studied the application of aluminium oxide in solar collectors to understand the potential heat transfer improvement with increasing nanoparticle concentration. Aluminium oxide was also studied by Sankar et al. [14], where the researchers studied the effects of non-uniform heating of nanoparticle-filled water in terms of understanding the buoyant transport and entropy generation for heat transfer applications. Pushpa et al. [15] studied the effects of convective heat transfer with copper nanoparticles in water with a thermally conductive fin and found that higher nanoparticle concentration improved heat transport rate with sensitivity to fin length and location. Despite the potential heat transfer improvement offered by adding nanoparticles into base fluids, the agglomeration of the nanoparticles within the base fluid can pose performance degradation, as Iacobazzi et al. [16] found that this phenomenon caused a reduction in the thermal conductivity of the base fluid. Therefore, a proper treatment to enhance the suspension of nanoparticles is required to maximise the potential gain in thermal conductivity and promote the base fluid's overall heat transfer coefficient.

Identifying an ideal colloidal suspension and fluid combination was an area where past researchers strived to improve [11]. The colloidal suspensions studied can be broadly categorised into metallic and non-metallic nanofluids. Sengul & Asmatulu [17] found that using metallic nanoparticles can pose environmental harm due to the inherent toxicity of many metals and metal oxides. They also found that the toxicity exhibited by several non-metallic nanoparticles was either low or non-existent [17]. Arvidsson et al. [18] conducted an extensive survey to establish the harm graphene particles pose to humans and animals. They concluded that graphene’s structure might be susceptible to permeation into humans via skin and lungs, but there was no known instance of toxicity regarding graphene exposure. Furthermore, the researchers elaborated that graphene did not pose any risk of potential tissue damage to the particle’s shape, unlike the case with carbon nanotubes (CNT) [18].

The present research aims to use CGNP-based colloidal suspension to understand its behaviour with the studied angled fins in the annular conduit. This colloidal suspension was chosen as it was found to be stable when functionalised, and the production method allows for mass production via environmentally friendly methods [19]. This benefit makes it ideal for large-scale production as it can be used in both industries as well as homes. The GNP properties used for CGNP production are shown in Table 1 [19, 20]. The CGNP colloidal suspension properties for three different concentrations achieved by Sadri et al. [21] were utilised for this investigation. The CGNP was later replicated and utilised by Almatar AbdRabbuh et al. [19] for their research to understand the potential heat transfer improvements offered by the various generated CGNP concentrations in a square and circular conduit. The method used by these authors involved the usage of dried clove bud extract and hydrogen peroxide, where the latter was used to graft the eugenol from the cloves onto the GNP. This resulted in the production of stable CGNP colloidal suspensions. The authors then produced CGNP concentrations of 0.025, 0.075 and 0.1 mass% [19, 21].

Table 1 Nanoplatelet properties of the GNP used in the production of CGNP by Almatar AbdRabbuh et al. [19]
Full size table

Setup of numerical simulation

Geometry design

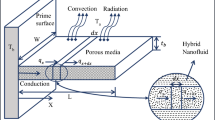
The annular geometry used is depicted in Fig. 1, where the swirling fins are angled at 20°. All dimensions shown in Fig. 1 were kept constant except for the fin angle, as the simulation was done on geometries with fins angled at 10°, 20°, 30° and 40°. Additionally, the influence of the density of angled fins was also investigated to compare the impact of spacing the angled fins with 200 mm against the original 100 mm spacing that was used for the rest of the simulations. The geometry with the lower angled fin density is shown in Fig. 2. It should be noted that the cases with annular geometry without fins have the same length and diameter specifications as the geometries in Figs. 1 and 2 to ensure the results obtained were comparable with the angled fin cases.

Fig. 1
figure 1

Geometry that was used for this investigation. It utilises angled fins at 10, 20, 30 and 40 degrees with 100 mm spacing between finned zones. All dimensions are in mm

Full size image
Fig. 2
figure 2

The geometry with the lower fin density is accomplished by having the spacings of 200 mm instead of the 100 mm spacing used in Fig. 1

Full size image

Boundary conditions and simulation setup

Since this research investigates heat transfer, a boundary must be selected where a constant heat flux could be applied. In this case, the outer wall was used as the location where the heat flux was applied. This was done to understand the impact of heat transfer purely due to swirling flow and not due to the heat transfer across the fins. The simulation was conducted such that 500 W of heat was supplied to the outer wall for an even heat flux at the boundary in all cases. This was in line with the experimental conditions conducted by Abdelrazek et al. [22], where an electrical heating tape was wrapped around the outer wall of the test section.

The fluid velocity at the inlet boundary was derived from 6 different flow rates between 2 and 12 L min−1 with increments of 2 L min−1 steps. The velocities resulting from those flow rates covered the Re number values from approximately 1000 at 2 L min−1 to approximately 6000 at 12 L min−1 covering the laminar, transitional and turbulent fluid flow velocities in this investigation. The fluid temperature at the inlet was kept constant at 293.15 K to represent the steady bulk fluid temperature entering the geometry. Table 2 summarises the boundary conditions and the solver settings used with ANSYS-Fluent [23]. The fluid properties used in this study were obtained from Almatar AbdRabbuh et al. [19]. The fluids were 0.025, 0.075 and 0.1 mass% CGNP suspensions dubbed as GNP0025, GNP0075 and GNP0100, respectively. The distilled water (DW) properties are also referred from Almatar AbdRabbuh et al. Almatar AbdRabbuh et al. [19] to ensure consistency with the author’s findings. The properties of these fluids are summarised in Table 3. The reported fluid properties by Almatar AbdRabbuh et al. [19] were based on the measurements made by Sadri et al. [21].

Table 2 Tabulation of the boundary condition and solver settings used for the simulation with ANSYS-Fluent [23]. The boundary condition values in parentheses represent the constant value used for all the simulations
Full size table
Table 3 Summary of the fluid properties used for this investigation. The fluid properties are obtained from the publication by Almatar AbdRabbuh et al. [19]
Full size table

Governing equations

Equations governing the numerical simulation

A few assumptions were made for this case study; namely, the fluid is Newtonian, the fluid is incompressible (constant density), there is no gravity acting on the fluid, and the fluid is a continuum. With these assumptions, the numerical solver used is that of a pressure-based solver, which adheres to the incompressible Navier–Stokes equations (NSE) shown from Eqs. 1–4 [24]. The equations are written in cylindrical coordinates as the case is cylindrical in nature.

Continuity:

$$\frac{1}{r}\frac{{\partial \left( {r V_{{\text{r}}} } \right)}}{\partial r} + \frac{1}{r}\frac{{\partial V_{{\uptheta }} }}{\partial r} + \frac{{\partial V_{{\text{z}}} }}{\partial z} = 0$$
(1)

Momentum equation with respect to r:

$$\frac{{\partial V_{{\text{r}}} }}{\partial t} + V_{{\text{r}}} \frac{{\partial V_{{\text{r}}} }}{\partial r} + \frac{{V_{{\uptheta }} }}{r}\frac{{\partial V_{{\text{r}}} }}{\partial \theta } + V_{{\text{z}}} \frac{{\partial V_{{\text{r}}} }}{\partial z} - \frac{{V_{{\uptheta }}^{2} }}{r} = - \frac{1}{\rho }\frac{\partial p}{{\partial r}} + \frac{\mu }{\rho }\left[ {\frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{\partial }{\partial r}\left( {rv_{{\text{r}}} } \right)} \right) + \frac{1}{{r^{2} }}\frac{{\partial^{2} V_{{\text{r}}} }}{{\partial \theta^{2} }} + \frac{{\partial^{2} V_{{\text{r}}} }}{{\partial z^{2} }} - \frac{2}{{r^{2} }}\frac{{\partial V_{{\text{r}}} }}{\partial \theta }} \right] + S_{{\text{r}}} .$$
(2)

Momentum equation with respect to \(\theta\):

$$\frac{{\partial V_{{\uptheta }} }}{\partial t} + V_{{\text{r}}} \frac{{\partial V_{{\uptheta }} }}{\partial r} + \frac{{V_{{\uptheta }} }}{r}\frac{{\partial V_{{\uptheta }} }}{\partial \theta } + V_{z} \frac{{\partial V_{{\uptheta }} }}{\partial z} + \frac{{V_{{\text{r}}} V_{{\uptheta }} }}{r} = - \frac{1}{\rho r}\frac{\partial p}{{\partial \theta }} + \frac{\mu }{\rho }\left[ {\frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{\partial }{\partial r}\left( {rv_{{\uptheta }} } \right)} \right) + \frac{1}{{r^{2} }}\frac{{\partial^{2} V_{{\uptheta }} }}{{\partial \theta^{2} }} + \frac{{\partial^{2} V_{{\uptheta }} }}{{\partial z^{2} }} + \frac{2}{{r^{2} }}\frac{{\partial V_{{\text{r}}} }}{\partial \theta }} \right] + S_{\theta } .$$
(3)

Momentum equation with respect to z:

$$\frac{{\partial V_{{\text{z}}} }}{\partial t} + V_{{\text{r}}} \frac{{\partial V_{{\text{z}}} }}{\partial r} + \frac{{V_{{\uptheta }} }}{r}\frac{{\partial V_{{\text{z}}} }}{\partial \theta } + V_{{\text{z}}} \frac{{\partial V_{{\text{z}}} }}{\partial z} = - \frac{1}{\rho }\frac{\partial p}{{\partial z}} + \frac{\mu }{\rho }\left[ {\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{{\partial V_{{\text{z}}} }}{\partial r}} \right) + \frac{1}{{r^{2} }}\frac{{\partial^{2} V_{{\text{z}}} }}{{\partial \theta^{2} }} + \frac{{\partial^{2} V_{{\text{z}}} }}{{\partial z^{2} }}} \right] + S_{{\text{z}}} .$$
(4)

Since the simulation also deals with heat transfer, the energy equation is also considered, as shown in Eq. 5.

Energy:

$$\frac{\partial i}{{\partial t}} + \frac{1}{r}\frac{{\partial \left( {r V_{{\text{r}}} i} \right)}}{\partial r} + \frac{1}{r}\frac{{\partial \left( { V_{{\uptheta }} i} \right)}}{\partial r} + \frac{{\partial \left( { V_{{\text{z}}} i} \right)}}{\partial z} = - \frac{1}{\rho }p\nabla \cdot {\mathbf{u}} + \frac{1}{\rho }\nabla \cdot \left( {k\nabla T} \right) + \frac{1}{\rho }{\Phi } + \frac{1}{\rho }S_{i} .$$
(5)

The term \({\Phi }\) is the energy dissipation function which is represented in Eq. 6.

$${\Phi } = \mu \left\{ {\begin{array}{*{20}c} {2\left[ {\left( {\frac{{\partial V_{{\text{r}}} }}{\partial r\cos \theta }} \right)^{2} + \left( {\frac{{\partial V_{{\uptheta }} }}{\partial r\sin \theta }} \right)^{2} + \left( {\frac{{\partial V_{{\text{z}}} }}{\partial z}} \right)^{2} } \right]} \\ { + \left( {\frac{{\partial V_{{\text{r}}} }}{\partial r\sin \theta } + \frac{{\partial V_{{\uptheta }} }}{\partial r\cos \theta }} \right)^{2} + \left( {\frac{{\partial V_{{\text{r}}} }}{\partial z} + \frac{{\partial V_{{\text{z}}} }}{\partial r\cos \theta }} \right)^{2} + \left( {\frac{{\partial V_{{\uptheta }} }}{\partial z} + \frac{{\partial V_{{\text{z}}} }}{\partial r\sin \theta }} \right)^{2} } \\ \end{array} } \right\} + \lambda \left( {\nabla \cdot {\mathbf{u}}} \right)^{2} .$$
(6)

The S term at the end of Eqs. 2–5 represents the source term that accounts for external contributions that need to be accounted for when solving the equations.

The numerical solver used to solve the momentum and energy equations in ANSYS-Fluent was the SIMPLEC algorithm by Doormaal and Raithby [25], which used the second-order upwind discretisation method to resolve the momentum and energy fluxes with second-order accuracy. The SIMPLEC algorithm is largely based on the SIMPLE algorithm developed by Patankar and Spalding [26], with the improvement in SIMPLEC allowing for greater pressure fluxes per iteration. This improvement provides quicker simulation time over the SIMPLE algorithm, which is still a groundbreaking algorithm in computational fluid dynamics in solving steady-state equations.

Heat transfer equations used

The heat transfer equations used in this investigation are shown in Eqs. 7 and 8 to quantify the heat transfer coefficient and the Nusselt number of the results, respectively. The results obtained from these equations helped translate the temperature data obtained from the simulation into meaningful heat transfer performance indicators.

$$\overline{h} = \frac{q}{{{\Delta }T}} .$$
(7)

From Eq. 7, \(\overline{h}\) is the average heat transfer coefficient, q is the heat flux, and \({\Delta }T\) is the difference between the averaged fluid temperature at the outer wall and the bulk temperature from the inlet.

$$\overline{{{\text{Nu}}}} = \frac{{\overline{h}D_{{\text{h}}} }}{k} .$$
(8)

From Eq. 8, \(\overline{{{\text{Nu}}}}\) is the average Nusselt number, \(D_{{\text{h}}}\) is the hydraulic diameter, and k is the thermal conductivity of the fluid. The \(\overline{{{\text{Nu}}}}\) number was obtained in Eq. 8 due to the \(\overline{h }\) value from Eq. 7 includes the averaged value of the temperature at the outer wall of the conduit.

Results and discussion

Grid generation

There were 9 different grids produced for this investigation where 4 grids possessed 100 mm spacing between finned zones for the 4 investigated fin angles (10°, 20°, 30° and 40°), respectively, and further 4 grids possessed 200 mm spacing between finned zones for the same investigated fin angles. The last grid was the annular geometry without fins. Refer to Figs. 1 and 2 for a visual representation of the described finned geometries. To comply with the chosen SST \(\kappa -\omega\) turbulence model, inflation layers were introduced to ensure Y + was about 1 for the highest flow rate simulated. The growth rate for the inflation layers was kept at a constant value of 1.2 for all cases. Furthermore, the number of inflation layers was also kept constant, with 5 layers at the inner wall and fin boundaries and 8 layers at the outer wall boundary. Figure 3 shows the magnified view of the unstructured grid used for each fin configuration, where the inflation layers at the inner wall and fins can be observed. The grid parameters were kept identical for all grids produced. The grids were then validated and had their associated error quantified in the next subsection. The grid properties are summarised in Table 4.

Fig. 3
figure 3

Enlarged view at the midsection (X = 0.5 m). All cases shown here are from the 100 mm spaced fin grids. The grids used for the 200 mm cases are similar as the grid generation parameters were kept constant. The inflation layers near the fin and inner wall can be seen in the figure

Full size image
Table 4 Properties of the grids used for the numerical simulations
Full size table

Grid validation and error quantification

The grid convergence study was performed to ensure that the chosen grid parameters were justified and the error band associated with them was quantified. For this study, the 30° angled fin cases had their grid validated with distilled water (DW) at 12 L min−1 for both the 100 mm and the 200 mm spaced fin cases. The 30° angle was arbitrarily chosen for validation as the error band could be extended to the cases with fin angles of 10°, 20° and 40°. Performing the grid convergence study for these two cases helped to optimise the computational cost for performing the simulations. Table 5 shows the grid properties used for the validation cases, whilst Fig. 4 shows the results from the grid convergence study. The result of the grid convergence study in Fig. 4 shows that the grid for the 30° angled fins is converging to the Richardson extrapolate value, which is effectively the average temperature when there is no grid spacing, as in the potential result without the limitation of a grid, like in the real world.

Table 5 Properties of the grids with the 30° angled fins which were used for the grid convergence study as part of the validation and error quantification
Full size table
Fig. 4
figure 4

Results for the grid convergence study performed on grids with 30° angled fins

Full size image

The Y + value of approximately 1 in Table 5 indicates that the height of the first cell near the wall is no higher than the laminar zone of the boundary layer. The usage of the SST \(\kappa -\omega\) turbulence model requires the grid to be compliant to a Y + value of approximately 1 as this two-equation model does not rely on wall functions to predict the fluid–wall interaction, and it needs to be resolved at the grid level. This method of resolving turbulence yields better vortex predictions as the fluid interaction with the wall is not overly smoothened using a wall function.

The grid spacing used in Fig. 4 was derived using the cell quantity by following Eq. 9.

$${\text{Grid spacing}} = \frac{1}{{\sqrt {\text{Cell quantity}} }}.$$
(9)

This methodology for grid validation is based on the work of Roach et al. [27], which is established as one of the accepted ways of conducting a proper grid refinement study for numerical simulations. The Richardson extrapolate shown in Fig. 4 is essentially the extrapolation method done on the coarse, medium and fine grid results to obtain the expected theoretical value if grid spacing is 0. Given that the expected error is now quantified for both fin spacing cases with the 30° fin angle, it is safe to state that the simulations carried out for this study have confidence of being within 0.2% of the actual result, which is unaffected by grid spacing.

Validation of results

The theoretical validation results shown in Fig. 5 compare the Nu number from the numerical simulation results with the results from the Gnielinski and Petukhov correlation equations, which are valid for smooth circular pipe flow [28, 29]. The Gnielinski and Petukhov Nu correlation equations shown in Eqs. 10 and 11, respectively, utilise the friction factor, f, approximated by using Eq. 12 by Petukhov [29], which works for a large range of Re numbers for a smooth conduit [30].

$${\text{Nu}}_{{{\text{Gn}}}} = \frac{{\frac{f}{8}\left( {{\text{Re}} - 1000} \right){\text{Pr}}}}{{1 + 12.7\left( \frac{f}{8} \right)^{\frac{1}{2}} \left( {{\text{Pr}}^{\frac{2}{3}} - 1} \right)}} .$$
(10)
$${\text{Nu}}_{{{\text{Pet}}}} = \frac{{\frac{f}{8} {\text{Re Pr}}}}{{1.07 + 12.7\left( \frac{f}{8} \right)^{\frac{1}{2}} \left( {{\text{Pr}}^{\frac{2}{3}} - 1} \right)}} .$$
(11)
$$f = \left( {0.790\ln {\text{Re}} - 1.64} \right)^{ - 2} .$$
(12)
Fig. 5
figure 5

Validating the numerical simulation results with the Gnielinski and Petukhov correlation equations for Nu. The comparison shows good conformity for Re numbers exceeding 3000

Full size image

The validation of the results for the non-finned annular conduit shown in Fig. 5 shows good conformity to both correlation equations, with the Gnielinksi values being much closer, with an average difference of 4.71% from the numerical simulation results. The Petukhov correlation equation, on the other hand, has a more pronounced difference compared to the numerical simulation results, with an average offset of 19.06%, which was expected given that the accuracy for Petukhov’s correlation equation is estimated for cases with Re numbers between 10,000 and \(5 \times 10^{6}\), which exceeds the maximum Re number of the studied cases. Nevertheless, the trend exhibited by the numerical simulation matched that of the result produced by the Petukhov correlation equation, thus further proving the validity of the numerical case study concerning heat transfer.

Heat transfer performance and pressure drop for 100 mm spaced fins.

The heat transfer performance was determined using the average temperature recorded from the entire surface area at the outer wall boundary between Z = 0.1 m and Z = 0.9 m, which keeps a 0.1 m space from both the inlet and outlet boundaries. This region was chosen to ensure that the inlet and outlet boundary conditions did not affect the temperature data. The pressure drop with each fin configuration was also noted for each tested concentration of colloidal suspension by comparing the difference in average pressure between Z = 0.1 m and Z = 0.9 m. Figure 6 shows the plots where the improvement with each fin configuration is being compared against the non-finned case for different concentrations of CGNP. The percentage increase for the heat transfer coefficient, h, and the Nusselt number, Nu, is identical as Nu is derived from the calculated h as shown in Eq. 8. Therefore, the h and Nu improvements are considered heat transfer improvement.

Fig. 6
figure 6

Bar charts indicating the increase in percentage for h and Nu against the different fin angles with respect to the non-finned case

Full size image

A trend is observed in Fig. 6 when the different fin angles were compared against the non-finned case for the tested flow rates. When the flow rate was in the laminar flow region (Re < 2000), the heat transfer performance was observed to be improving with increasing angled fins’ steepness. This improvement occurred because the fluid was swirling in the counterclockwise direction, as directed by the angled fins, and the tip of the fin generated no strong vortex at such low flow rates. The swirl induced by the angled fin caused the local fluid velocity to be higher to achieve the same flow rate, thus improving heat transfer performance. The heat transfer improvement due to swirling flow was the main reason for the increasing heat transfer improvement in low Re cases with increasing angled fin steepness.

However, at the start of the transitional region at Re ≈ 2000, the heat transfer performance was higher for the 10° fin angle than it was for the 20° and 30° angles, before having a sharp increase in heat transfer performance at the 40° angle. Furthermore, the heat transfer performance with the 30° angle at the Re ≈ 2000 flow velocity dropped below that of the non-finned case. The lower performance at the 30° angle can also be observed at Re ≈ 3000 (at the end of the transitional flow), but the performance was still higher than that of the non-finned case. Once the flow velocity entered the turbulent region (Re > 3000), the 20° angled fin was not favourable because better performance could be achieved with the 10° for a much lower pressure drop, as shown in Fig. 7.

Fig. 7
figure 7

The bar charts show the increase in pressure drop against the different fin angles with respect to the non-finned case. Higher percentages of pressure drop indicate a lower performance

Full size image

The increase in pressure drop, which is not desirable in heat transfer applications, cannot be ignored, as shown by the plots in Fig. 7. The pressure drop increased with the increased fluid velocity, fin angle and CGNP concentration. Despite the increase in pressure drop with increasing fin angles indicated in Fig. 7, the improvement in heat transfer performance can outweigh this loss of pressure, as indicated in Figs. 6 and 8. For flows in the turbulent regime, indicated by Re values that are greater than 3000, the 10° and 40° angled fins are recommended over the 20° and 30° angled fins since the former two angles provided a noticeable gain in heat transfer performance which justifies the pressure drop associated with the usage of the proposed angled fin design. Additionally, the increase in pressure drop for a 0.8 m length was found to be no more than 35 Pa at the highest flow rate tested for the 40° angled fin case, an insignificant pressure drop in some applications, especially when the improvement in heat transfer performance of about 8% allows for compact heat exchanger design.

Fig. 8
figure 8

Plots of heat transfer coefficient h against the different fin configurations. In cases with transitional and turbulent flows, the 10° and 40° angled fins performed the best, whilst the 20° and 30° angled fins are only viable for laminar flows

Full size image

The role of increasing CGNP concentration on heat transfer performance.

CGNP0100 provided the lowest increase in heat transfer performance when comparing the different concentrations of CGNP used as the working fluid for each angled fin case. This seems to be because CGNP0100 already has the best heat transfer performance amongst the non-finned cases, as shown in Fig. 8, and the heat transfer improvement offered by the usage of angled fins was not as significant. This was evident when CGNP0100 showed the highest h values, followed by CGNP0075, CGNP0025 and DW in Fig. 8. On the other hand, Fig. 6 shows that DW had the best improvement with angle fins, followed by CGNP0025, CGNP0075 and CGNP0100. This concludes that the higher the CGNP concentration, the lower the potential performance gain of using angled fins (all tested angles). However, this does not mean that CGNP worsens the heat transfer performance; on the contrary, it had further improved the heat transfer coefficient, with the best heat transfer coefficient being achieved using the 40°angled fins with CGNP0100, as shown in Fig. 8(f).

Difference in heat transfer performance and pressure drop between 100 and 200 mm spaced fins.

The spacing between the finned zones and its impact on heat transfer and pressure drop performance was considered in this study. To accomplish this objective, the main case, which compared 100 mm spaced fins with all 4 tested fluids for 4 different fin angles, was tested against the geometry with 200 mm spaced finned zones. However, only DW was used in this comparison as the colloidal suspension performance concerning concentration was already established using the 100 mm spaced fin case. This section highlights the potential effect fin spacing has on heat transfer performance. Future work is needed to identify the optimal spacing for the best achievable heat transfer performance. Figure 9 shows the increase in h and Nu for the tested angled fin cases over their respective non-finned counterpart.

Fig. 9
figure 9

The bar charts show the increase in percentage for h and Nu against the different fin angles with respect to the non-finned case

Full size image

The behaviour shown in Fig. 6 is shown in Fig. 9, where heat transfer performance improved notably when the fluid velocity was in the laminar regime. Poor performance was seen at the fin angles of 20° and 30° for the fluid velocity in the transitional regime. The performance for turbulent flows also remained similar, with the best performance being observed in the 40° angled fin case, whilst the 20° and 30° angled fin cases performed similarly to the 10° angled fin case. The 200 mm spaced fins had poorer observable heat transfer performance. However, the increased spacing between fins also resulted in a lower pressure drop, as indicated in Fig. 10, compared to Fig. 7.

Fig. 10
figure 10

The bar charts show the increase in pressure drop against the different fin angles with respect to the non-finned case. Higher percentages of pressure drop indicate a lower performance

Full size image

Figure 10 shows that using a wider spacing between fins reduces the pressure drop, though at the expense of heat transfer performance. Since the pressure drop increase at the highest tested flow rate was found to be less than 25 Pa for a 0.8 m conduit, the usage of the 100 mm spaced fins is better justified as it yielded an increase of almost 8% in heat transfer performance at 40° for the highest flow rate studied (Re = 6000). This gives about a 3% improvement in heat transfer performance over the 200 mm spaced fins which can help the augmentation of better heat exchanger efficiency.

Visualising and understanding the influence of the angled fins on heat transfer performance.

To better understand the behaviour that led to the results in Figs. 6–10, flow visualisation via streamlines and Q-criterion iso-surface plot was done for the 12 L min−1 DW case in Fig. 11. It shows that greater turbulence intensity was observed in the fins’ wake as the fin angle increased. This resulted in higher recirculation intensity in the form of swirling longitudinal vortices, which helped to increase the local h and Nu. However, the increased radial recirculation intensity as the angled fins got steeper indicated that the potential pressure drop associated with steeper angles is progressively higher, which is especially true for the 40° angled fin case. Furthermore, the intensity of the swirling effect was found to increase heat transfer performance as a greater swirling effect due to steeper angled fins results in higher local flow velocities to achieve the same flow rate. This phenomenon is supported by past research where swirling flows were induced by a twisted tape [1, 6, 31, 32]. However, using angled fins is advantageous compared to using a twisted tape design as it minimises the pressure drop by not restricting the flow channel and allowing mixing to occur, thus promoting better thermal convection from the fluid. On the other hand, the characteristic of encouraging mixing could explain why the usage of higher CGNP concentrations provided minor improvements in the increase in the heat transfer performance; as fluid viscosity increased, the tendency to create swirling flow and swirling longitudinal vortices reduced.

Fig. 11
figure 11

Streamlines indicate the path taken by the DW fluid at the midsection of 4 angled fin cases for the 12 L min−1 flow rate. The iso-surface Q-criterion plot displays the turbulence intensity produced at the wake of the fins

Full size image

The impact of the swirling longitudinal vortices on heat transfer performance

Upon investigating the vortical structure produced at the wake of the finned zone at Z = 0.525 m, about 20 mm after the trailing edge of the fin, it is evident that the size of the swirling longitudinal vortices played a vital role in the heat transfer performance of the conduit. The 4 L min−1 or Re ≈ 2000 cases were used to obtain the streamlines in Fig. 12, as this velocity provided the best insight into understanding the performance characteristic of the tested fin angles. In Fig. 12, bigger longitudinal vortices were observed when using the 10° and 40° angle fins, which were found to be responsible for the improved heat transfer performance, as heat from the thermal boundary layer was better mixed with the inviscid region of the fluid flow. This finding was supported by water and the CGNP–water colloidal suspension having a Pr number greater than 1, which indicates that the thermal boundary layer is smaller than the velocity boundary layer. Heat transfer was noticeably improved when the larger longitudinal vortices encouraged the mixing of the heated fluid in the thermal boundary region with the fast-moving cooler fluid in the inviscid region. Additionally, the sudden increase in heat transfer performance for the 40° case can be attributed to the interaction between the radial recirculation and the swirling longitudinal vortices, as shown in Fig. 11.

Fig. 12
figure 12

Vortical structure produced at 5 mm region of the trailing edge of the fin at X = 0.525 m at Re \(\approx\) 2000 for the 4 different angled fin cases

Full size image

A notable result in Fig. 6(b) shows that the 30° angled fin under Re \(\approx\) 2000 yields negative heat transfer performance, which shows that having small longitudinal vortices that only occur within the thermal boundary layer worsens the overall heat transfer performance. However, larger longitudinal vortices were formed when this fin angle was used in fully laminar and turbulent cases where Re < 2000 and Re > 3000, which yielded better heat transfer performance for the 30° angled fin over the non-finned case. The similar trend observed in Figs. 7 and 8 indicates that the reduction in fin density does not alter the overall size and structure of the longitudinal vortices. However, the reduced number of swirling longitudinal vortices caused a lower heat transfer performance.

Conclusions

The heat transfer performance improvement of utilising CGNP-based colloidal suspensions, angled fins and the associated pressure loss was investigated numerically, and the results are presented in this paper. The usage of CGNP can be justified as it is non-toxic, improves thermal conductivity and can be easily scaled for mass production. Several conclusions could be drawn from this investigation, which is systematically presented here:

  1. (a)

    The usage of angled fins enhances the heat transfer performance of the annular geometry compared to the similar non-finned geometry.

  2. (b)

    The role played by swirling longitudinal vortices was noticeably apparent as it caused significant differences in results, especially in the critical condition identified, the 30° angled fin case in the transitional regime. The swirling flow itself could not improve the heat transfer enough when the small swirling longitudinal vortices trapped the heat within the thermal boundary region.

  3. (c)

    The optimal fin angle that can be recommended varies according to the Re number of the flow within the annular geometry. The fin angles of 10° and 40° were found to yield the best results at all the flow rates tested (up to 8%). The 40° angled fin provided the best heat transfer performance despite causing the highest pressure drop (an increment of 35 Pa over the non-finned geometry across 0.8 m).

  4. (d)

    Higher concentrations of CGNP increase pressure drop insignificantly (in the specified range). This finding can be attributed to the higher viscosity of the colloidal suspension with the increasing CGNP concentrations (in the specified range).

  5. (e)

    Using an annular flow type heat exchanger with the optimal fin angle can be justified for improved heat transfer performance, especially in cases where pressure losses are not of significant concern.

  6. (f)

    Using the optimal fin angle coupled with the CGNP-based colloidal suspension for the heat exchanging fluid could be used to develop compact and efficient heat exchanger design for various heat transfer applications.

Despite this research’s objective of understanding the performance impact of CGNP-based colloidal suspension in an annular domain being met, some limitations persist and can be addressed in a future publication. Such limitations include the identification of the optimal angled fin as well as the optimal fin density. The increase in pressure drop will get higher when steeper fin angles, as well as when a more compact fin arrangement is utilised (to be addressed in future work); there can still be a point where the maximum gain in heat transfer performance is observable. Determining the optimal angle and fin density can be beneficial in use cases that need the maximum gain in heat transfer performance, as the requirement of the heat exchanger to be compact allows for a more significant pressure drop.