Thermal and flow investigation of MHD natural convection in a nanofluid-saturated porous enclosure: an asymptotic analysis

Abstract

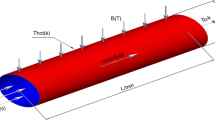
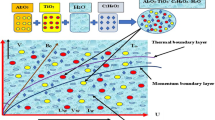
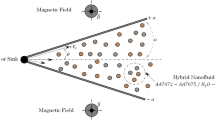
In the present investigation, asymptotic solutions are obtained regarding the laminar natural convection of a nanofluid in a porous enclosure subject to internal heating and magnetic field, which appears in a plethora of industrial and bioengineering applications. The complicated nature of the nanofluids along with the computational time needed for the magnetohydrodynamic numerical simulations makes this problem too difficult to face with. Hence, the innovation of this study relies on providing a first-principles approach that includes three kinds of widely utilized nanoparticles (Cu, Al₂O₃ and TiO₂) dispersed in aqueous suspension by incorporating a unified way for describing the nanofluid thermal conductivity and viscosity. In addition, the effect of the magnetic field, internal heating, porous medium permeability as well as nanoparticle size and volume fraction is examined via the derived analytical relationships. In brief, the current study suggests that the increase in the magnetic field intensity and the decrease in the medium permeability tend to suppress the nanofluid flow, thus resulting in deterioration of the heat transfer. This deterioration also occurs when the nanofluid becomes denser and the nanoparticles enlarge. Conversely, increasing the internal heating reinforces the convective currents in favor of cooling process. Finally, the present asymptotic solutions are expected to be very useful in various scientific fields given the rapidly growing interest in nanofluids.

Appendix

Derivation of the governing dimensionless equations

The governing system of two-dimensional steady-state, incompressible, MHD equations has been presented in Eqs. (1)–(4). Taking the derivative of Eqs. (2) and (3) with respect to z and x, respectively, and considering the continuity equation, Eq. (1):

$$u\frac{{\partial^{2} u}}{\partial z\partial x} + w\frac{{\partial^{2} u}}{{\partial z^{2} }} = - \frac{1}{{\rho_{\text{nf}} }}\frac{{\partial^{2} p}}{\partial z\partial x} + v_{\text{nf}} \frac{{\partial^{3} u}}{{\partial z\partial x^{2} }} + v_{\text{nf}} \frac{{\partial^{3} u}}{{\partial z^{3} }} - \frac{{\sigma_{\text{nf}} \,B_{\text{o}}^{2} }}{{\rho_{\text{nf}} }}\frac{\partial u}{\partial z} - \frac{{v_{\text{nf}} }}{K}\frac{\partial u}{\partial z}$$

(33)

$$u\frac{{\partial^{2} w}}{{\partial x^{2} }} + w\frac{{\partial^{2} w}}{\partial x\partial z} = - \frac{1}{{\rho_{\text{nf}} }}\frac{{\partial^{2} p}}{\partial x\partial z} + v_{\text{nf}} \frac{{\partial^{3} w}}{{\partial x^{3} }} + v_{\text{nf}} \frac{{\partial^{3} w}}{{\partial x\partial z^{2} }} + g\beta_{\text{nf}} \frac{\partial T}{\partial x} - \frac{{v_{\text{nf}} }}{K}\frac{\partial w}{\partial x}$$

(34)

Subtracting Eqs. (34) from (33):

$$u\frac{\partial }{\partial x}\left( {\frac{\partial u}{\partial z} - \frac{\partial w}{\partial x}} \right) + w\frac{\partial }{\partial z}\left( {\frac{\partial u}{\partial z} - \frac{\partial w}{\partial x}} \right) = v_{\text{nf}} \left( {\frac{{\partial^{3} u}}{{\partial x^{2} \partial z}} + \frac{{\partial^{3} u}}{{\partial z^{3} }} - \frac{{\partial^{3} w}}{{\partial x^{3} }} - \frac{{\partial^{3} w}}{{\partial z^{2} \partial x}}} \right) - \frac{{\sigma_{\text{nf}} \,B_{\text{o}}^{2} }}{{\rho_{\text{nf}} }}\frac{\partial u}{\partial z} - g\beta_{\text{nf}} \frac{\partial T}{\partial x} - \frac{{v_{\text{nf}} }}{K}\left( {\frac{\partial u}{\partial z} - \frac{\partial w}{\partial x}} \right)$$

(35)

The stream function ψ(x, z) is related to velocity components u and v via:

$$u = \frac{\partial \psi }{\partial z},\quad w = - \frac{\partial \psi }{\partial x}$$

(36)

Substituting Eqs. (36) in (35):

$$\frac{\partial \psi }{\partial z}\frac{\partial }{\partial x}\underbrace {{\left( {\frac{{\partial {}^{2}\psi }}{{\partial x^{2} }} + \frac{{\partial^{2} \psi }}{{\partial z^{2} }}} \right)}}_{{\nabla^{2} \psi }} - \frac{\partial \psi }{\partial x}\frac{\partial }{\partial z}\underbrace {{\left( {\frac{{\partial^{2} \psi }}{{\partial x^{2} }} + \frac{{\partial^{2} \psi }}{{\partial z^{2} }}} \right)}}_{{\nabla^{2} \psi }} = v_{\text{nf}} \underbrace {{\left( {\frac{{\partial^{4} \psi }}{{\partial x^{4} }} + 2\frac{{\partial^{4} \psi }}{{\partial x^{2} \partial z^{2} }} + \frac{{\partial^{4} \psi }}{{\partial z^{4} }}} \right)}}_{{\nabla^{4} \psi }} - \frac{{\sigma_{\text{nf}} \,B_{\text{o}}^{2} }}{{\rho_{\text{nf}} }}\frac{{\partial^{2} \psi }}{{\partial z^{2} }} - g\beta_{\text{nf}} \frac{\partial T}{\partial x} - \frac{{v_{\text{nf}} }}{\rm K}\underbrace {{\left( {\frac{{\partial {}^{2}\psi }}{{\partial x^{2} }} + \frac{{\partial^{2} \psi }}{{\partial z^{2} }}} \right)}}_{{\nabla^{2} \psi }}$$

(37)

Substituting also Eq. (36) in energy equation, namely Eq. (4), it turns out that:

$$\frac{\partial \psi }{\partial z}\frac{\partial T}{\partial x} - \frac{\partial \psi }{\partial x}\frac{\partial T}{\partial z} = a_{\text{nf}} \nabla^{2} T + \frac{Q}{{\left( {\rho \,c_{\text{p}} } \right)_{\text{nf}} }}$$

(38)

Next, the dimensional form of the stream function and energy equations are derived via considering the following magnitudes:

$$X = \frac{x}{h},\quad Z = \frac{z}{h},\quad \varPsi = \frac{\psi }{{a_{\text{nf}} }},\quad \varTheta = \frac{{T\left( {\rho c_{\text{p}} } \right)_{\text{nf}} a_{\text{nf}} }}{{h^{2} Q}}$$

(39)

Thus Eqs. (37) and (38) result in Eqs. (40) and (41), respectively:

$$\nabla^{4} \varPsi = {\rm Pr}_{\text{nf}}^{ - 1} \frac{{\partial (\nabla^{2} \varPsi ,\varPsi )}}{\partial (X,Z)} + {\text{Ha}}_{\text{nf}}^{2} \frac{{\partial^{2} \varPsi }}{{\partial Z^{2} }} + {\text{Ra}}_{\text{nf}} \frac{\partial \varTheta }{\partial X} + {\text{Da}}^{1} \nabla^{2} \varPsi$$

(40)

$$\nabla^{2} \varTheta + 1 = \frac{\partial (\varTheta ,\varPsi )}{\partial (X,Z)}$$

(41)

where the dimensionless numbers Da, Pr_nf, Ra_nf and Ha_nf have already been defined in Eqs. (15)–(18) of the main part of this study. Besides, X, Z, Θ and Ψ are converted to x, z, T and ψ, respectively, for the sake of simplicity.

Derivation of the ordinary differential equations using the asymptotic expansions method

The governing parameter of the present problem is ε, which can be defined as ε ≡ L⁻¹ ≪ 1, where L is the aspect ratio of the cavity that is very large, as it has already been stressed. The core flow covers most of the cavity and its solution relies on the length scales ξ and z (Eq. 24).

Similarly to [20,21,22], the stream function and the temperature fields are expanded with respect to ξ, z as follows:

$$\psi = \psi_{0} (\xi ,z) + L^{ - 1} \,\psi_{1} (\xi ,z) + L^{ - 2} \,\psi_{2} (\xi ,z) + \cdots$$

(42)

$$T = L^{2} \,T_{0} (\xi ,z) + L\,T_{1} (\xi ,z) + T_{2} (\xi ,z) + L^{ - 1} \,T_{3} (\xi ,z) + \cdots$$

(43)

These expansions are substituted into the flow and energy equations and their boundary conditions, which have been analyzed in the main part of the study, for the purpose of obtaining a system of coupled partial equations for the stream function and temperature for every order of magnitude of L.

Thus, substituting Eqs. (42), (43) into (40) in terms of ξ and z:

$$\begin{aligned} & L^{ - 4} \frac{{\partial^{4} \psi_{0} }}{{\partial \xi^{4} }} + 2L^{ - 2} \frac{{\partial^{4} \psi_{0} }}{{\partial \xi^{2} \partial z^{2} }} + \frac{{\partial^{4} \psi_{0} }}{{\partial z^{4} }} + L^{ - 5} \frac{{\partial^{4} \psi_{1} }}{{\partial \xi^{4} }} + 2L^{ - 3} \frac{{\partial^{4} \psi_{1} }}{{\partial \xi^{2} \partial z^{2} }} + L^{ - 1} \frac{{\partial^{4} \psi_{1} }}{{\partial z^{4} }} + \cdots \\ & \quad = {\rm Pr}_{\text{nf}}^{ - 1} \left[ {L^{ - 3} \frac{{\partial (\partial^{2} \psi_{0} /\partial \xi^{2} ,\psi_{0} )}}{\partial (\xi ,z)} + L^{ - 1} \frac{{\partial (\partial^{2} \psi_{0} /\partial z^{2} ,\psi_{0} )}}{\partial (\xi ,z)}} \right] \\ & \quad \quad + \,{\rm Pr}_{\text{nf}}^{ - 1} \left[ {L^{ - 4} \frac{{\partial (\partial^{2} \psi_{1} /\partial \xi^{2} ,\psi_{1} )}}{\partial (\xi ,z)} + L^{ - 2} \frac{{\partial (\partial^{2} \psi_{1} /\partial z^{2} ,\psi_{1} )}}{\partial (\xi ,z)}} \right] + \cdots \\ & \quad \quad + \,{\text{Ha}}_{\text{nf}}^{2} \frac{{\partial^{2} \psi_{0} }}{{\partial z^{2} }} + {\text{Ha}}_{\text{nf}}^{2} L^{ - 1} \frac{{\partial^{2} \psi_{1} }}{{\partial z^{2} }} + \cdots \\ & \quad \quad + \,\underbrace {{{\text{Ra}}_{\text{nf}} L}}_{{{\text{Rs}}_{\text{nf}} }}\frac{{\partial {\rm T}_{0} }}{\partial \xi } + \underbrace {{{\text{Ra}}_{\text{nf}} }}_{{{\text{Rs}}_{\text{nf}} L^{ - 1} }}\frac{{\partial {\rm T}_{1} }}{\partial \xi } + \cdots \\ & \quad \quad + \,{\text{Da}}^{ - 1} L^{ - 1} \frac{{\partial^{2} \psi_{0} }}{{\partial \xi^{2} }} + {\text{Da}}^{ - 1} \frac{{\partial^{2} \psi_{0} }}{{\partial z^{2} }} + {\text{Da}}^{ - 1} L^{ - 2} \frac{{\partial^{2} \psi_{1} }}{{\partial \xi^{2} }} + {\text{Da}}^{ - 1} L^{ - 1} \frac{{\partial^{2} \psi_{1} }}{{\partial z^{2} }} + \cdots \\ \end{aligned}$$

(44a)

Next, the terms of order one and L⁻¹ are equalized:

$$\frac{{\partial^{4} \psi_{0} }}{{\partial z^{4} }} - \left( {{\text{Ha}}_{\text{nf}}^{2} + {\text{Da}}^{ - 1} } \right)\frac{{\partial^{2} \psi_{0} }}{{\partial z^{2} }} = {\text{Rs}}_{\text{nf}} \frac{{\partial T_{0} }}{\partial \xi }$$

(44b)

$$\frac{{\partial^{4} \psi_{1} }}{{\partial z^{4} }} = {\rm Pr}_{\text{nf}}^{ - 1} \frac{{\partial (\partial^{2} \psi_{0} /\partial z^{2} ,\psi_{0} )}}{\partial (\xi ,z)} + \left( {{\text{Ha}}_{\text{nf}}^{2} + {\text{Da}}^{ - 1} } \right)\frac{{\partial^{2} \psi_{1} }}{{\partial z^{2} }} + {\text{Rs}}_{\text{nf}} \frac{{\partial T_{1} }}{\partial \xi } + {\text{Da}}^{ - 1} \frac{{\partial^{2} \psi_{0} }}{{\partial \xi^{2} }}$$

(44c)

Similarly, substituting Eqs. (42), (43) into (41) at order L², L and 1 it is obtained, respectively, as:

$$\frac{{\partial^{2} T_{0} }}{{\partial z^{2} }} = 0$$

(45a)

$$\frac{{\partial^{2} T_{1} }}{{\partial z^{2} }} = \frac{{\partial T_{0} }}{\partial \xi }\frac{{\partial \psi_{0} }}{\partial z}$$

(45b)

$$\frac{{\partial^{2} T_{2} }}{{\partial z^{2} }} = - 1 - \frac{{\partial^{2} T_{0} }}{{\partial \xi^{2} }} + \frac{{\partial T_{1} }}{\partial \xi }\frac{{\partial \psi_{0} }}{\partial z} + \frac{{\partial T_{0} }}{\partial \xi }\frac{{\partial \psi_{1} }}{\partial z} - \frac{{\partial T_{1} }}{\partial z}\frac{{\partial \psi_{0} }}{\partial \xi }$$

(45c)

The solution of Eq. (45a) with the adiabatic boundary conditions $\partial T_{0} /\partial z = 0$ at $z = \pm 0.5$ is:

$$T_{0} = \theta_{0} (\xi )$$

(46)

where θ₀ is a function of ξ, independent of z.

Derivation of the analytical solutions

Following the analysis of [20,21,22], only the stream functions of order one and temperatures of order L² are going to be analyzed which give a satisfactory picture of the nanofluid flow and heat transfer for the core region. Focusing on Eq. (44b), its complementary equation is:

$$\frac{{\partial^{4} \psi_{0} }}{{\partial z^{4} }} - \left( {{\text{Ha}}_{\text{nf}}^{2} + {\text{Da}}^{ - 1} } \right)\frac{{\partial^{2} \psi_{0} }}{{\partial z^{2} }} = 0$$

(47)

The general solution of the complementary equation is:

$$\psi_{0,c} = A(\xi )\cosh \left[ {\left( {{\text{Ha}}_{\text{nf}}^{2} + {\text{Da}}^{ - 1} } \right)z} \right] + B(\xi )\sinh \left[ {\left( {{\text{Ha}}_{\text{nf}}^{2} + {\text{Da}}^{ - 1} } \right)z} \right] + C(\xi )z + D(\xi )$$

(48a)

while its particular solution is in the same manner as [20,21,22]:

$$\psi_{{0,{\text{p}}}} = - \frac{{{\text{Rs}}_{\text{nf}} \theta_{0}^{{\prime }} }}{{{\text{Ha}}^{2} + {\text{Da}}^{ - 1} }}\frac{{z^{2} }}{2}$$

(48b)

Substituting the boundary conditions pertaining to ψ₀, namely Eqs. (19) and (20) of the main part of the present study, and adding the particular and general solutions:

$$\psi_{0} = \frac{{{\text{Rs}}_{\text{nf}} \theta_{0}^{{\prime }} }}{{{\text{Ha}}^{2} + {\text{Da}}^{ - 1} }} \cdot G(z)$$

(49)

where

$$G(z) = \frac{1}{2}\,\left( {\frac{{\cosh \left( {\sqrt {{\text{Ha}}^{2} + {\text{Da}}^{ - 1} } z} \right)}}{{\sqrt {{\text{Ha}}^{2} + {\text{Da}}^{ - 1} } \,\sinh \left( {\sqrt {{\text{Ha}}^{2} + {\text{Da}}^{ - 1} } /2} \right)}} - \frac{{\coth \left( {\sqrt {{\text{Ha}}^{2} + {\text{Da}}^{ - 1} } /2} \right)}}{{\sqrt {{\text{Ha}}^{2} + {\text{Da}}^{ - 1} } }} + \frac{1}{4} - z^{2} } \right)$$

(50)

Integrating in z Eq. (45c) and applying the boundary condition $\left. {\partial T_{2} /\partial z} \right|_{z = \pm 0.5} = 0$, the only consistent solution according to [21, 22] should obey the equation for θ₀:

$$\theta_{0}^{{\prime \prime }} + a_{\text{m}} \,R_{1}^{2} \,\left( {\theta_{0}^{{\prime }} } \right)^{2} \theta_{0}^{{\prime \prime }} + 1 = 0$$

(51)

where

$$\alpha_{m} = \frac{3}{{\left( {{\text{Ha}}^{2} + {\text{Da}}^{ - 1} } \right)^{2} }}\int\limits_{{{\raise0.5ex\hbox{$\scriptstyle { - 1}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}}}^{{{\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}}} {G(z)^{2} {\text{d}}z} \Rightarrow$$

(52)

Following the analysis of [21], the first integration of Eq. (51) considering the symmetry condition of the solution yields:

$$\theta_{0}^{{\prime }} = a_{\text{m}}^{ - 1/2} \,R_{1}^{ - 1} \,\left[ {F_{\text{m}}^{ + } (\xi ) + F_{\text{m}}^{ - } (\xi )} \right]$$

(53)

where

$$F_{\text{m}}^{ \pm } (\xi ) = \left\{ {\frac{3}{2}a_{\text{m}}^{1/2} \,R_{1} \,\left( {\frac{1}{2} - \xi } \right) \pm \left[ {1 + \frac{9}{4}a_{\text{m}} \,R_{1}^{2} \left( {\xi - \frac{1}{2}} \right)^{2} } \right]^{1/2} } \right\}^{1/3}$$

(54)

Moreover, using $\sinh y_{\text{m}} = \sinh^{ - 1} \left[ {\frac{3}{2}a_{\text{m}}^{1/2} \,{\text{Rs}}_{\text{nf}} \left( {\xi - \frac{1}{2}} \right)} \right]$ with a further integration, a closed-form solution of the core stream function, vertical velocity and temperature is produced (Eqs. (25)–(27), respectively) where $y_{{{\text{m}},0}} = \sinh^{ - 1} \left( {\frac{3}{4}a_{\text{m}}^{1/2} {\text{Rs}}_{\text{nf}} } \right).$