Introduction

The decay constant λ establishes the link between the number of atoms N of a particular radionuclide in a sample and their expected radioactive decay rate A, i.e. λ = A/N [1]. The value of λ-or inversely the half-life T1/2 = ln(2)/λ-is invariable in space and time, in spite of recent claims of variability in decay rate measurements erroneously ascribed to solar influences [2,3,4,5,6,7,8,9,10,11]. Accurate values for the decay constant or half-life of trans-uranium nuclides are required for accounting of nuclear material, assay of targets used in nuclear physics experiments, and characterisation of isotopic mixtures for radioanalytical purposes. Whereas mass spectrometry is the most accurate measurement method to determine isotope ratios in nuclear material, also relative activity measurements can be applied with good accuracy provided that the ratio of the decay constants of the isotopes are well known.

A coordinated research project of the IAEA [12] has identified a need for more accurate decay data for 243Am, comprising the half-life value as well as the alpha and gamma emission characteristics. The longest-lived and most common isotopes of americium, 241Am and 243Am, have half-lives of 432.6 (6) a and 7367 (23) a, respectively [13]. Both are alpha emitters. Whereas any primordial americium on Earth has decayed away, it is produced in nuclear reactors by multiple neutron captures in 239Pu and subsequent β– decay of 241Pu and 243Pu. A ton of spent nuclear fuel contains about 100 g of americium, thus representing one of the most troublesome long-term radiotoxicity hazards in nuclear waste. Partitioning and transmutation of actinium and curium are being considered to reduce long-term radiotoxicity and heat load of spent fuel [14]. Americium can also be used in Radioisotope Thermoelectric Generators (RTGs) and Radioisotope Heater Units (RHUs) in space nuclear power systems [15].

Recently, the Joint Research Centre (JRC) and the Commissariat à l’énergie atomique et aux énergies alternatives (CEA) have collaborated in the production and certification of an 243Am reference material for the quantification of Am in an unknown sample by isotope dilution mass spectrometry (IDMS) [16,17,18,19]. This responds to a pressing need in the fields of nuclear safeguards and security, nuclear forensics, and accountability in the nuclear fuel cycle [20, 21]. The reference material contains a mixture of 241Am and 243Am, which has been carefully analysed for the amount content by IDMS and for isotope amount ratios by thermal ionisation mass spectometry (TIMS). In addition, absolute 243Am + 241Am and relative 243Am/241Am radioactivity measurements were performed as a redundancy check of the certified amount values.

In this work, the isotope amount content and activity measurements are used to derive a value for the 243Am half-life. A comparison is made with previously published measurement results [23,24,25,26,27,28,29,30,31] and evaluated values by the Decay Data Evaluation Project (DDEP) and Nuclear Data Sheets (NDS) [13, 32]. Figure 1 shows a schematic overview of the techniques used and the observables obtained through a relative and absolute method, as explained futher on in the paper. All uncertainty values in this work pertain to the standard uncertainty.

Fig. 1
figure 1

Scheme of the methodology. The relative method derives the half-life ratio between 243Am and 241Am from the isotopic abundance ratio of a mixed material via TIMS and the activity ratio via alpha spectrometry. A literature value of \(T_{1/2} (^{241} {\text{Am}})\) is then used to calculate \(T_{1/2} (^{243} {\text{Am}})\). The absolute method uses additional data of the americium content determined via IDMS and the absolute activity of 243Am and 241Am, to determine the specific activity of 243Am

Full size image

Measurement methods

Material production

The starting solution, containing four milligram americium source material with mass fractions of 88% 243Am and 12% 241Am, was made available by the CEA/L2AT (ATalante Analysis Laboratory). The solution was passed through TRU resin (Triskem, France) to remove the impurities, and the americium was then eluted with 5 mL 0.01 M nitric solution. The purified americium solution was shipped to JRC-Geel and diluted upon arrival in 2400 mL 1 M nitric acid solution to obtain an Am mass fraction of 1.5 µg (Am) g−1 (solution). This Am fraction was considered suitable for various mass spectrometry measurements (e.g. TIMS, ICP-MS). The solution was allowed enough time to homogenise before being dispensed into pre-cleaned screw-cap ampoules. In total, 587 units were prepared, each unit containing approximately 5 µg of americium in 1 M nitric acid solution [16, 19]. Out of the produced units, eighteen were selected for the characterisation of the material.

Amount content by IDMS

The characterisation of the mass content of 243Am was established by IDMS as a primary measurement method. In IDMS, the amount of an element in the sample is determined on the basis of additions of known amounts of the same element with different isotopic composition (called spike). By measuring the change in isotopic composition of the blend (sample-spike mixture) by mass spectrometry, the unknown amount of the element in the sample can be calculated. In the absence of a suitable 241Am spike CRM for IDMS measurements, an alternative approach was applied. An 241Am spike was produced from highly enriched 241Pu (m(241Pu)/m(Pu) = 0.993) material available at JRC-Geel. The purification of approximately 2 mg 241Pu material was done by anion exchange separation. The ingrown 241Am, produced by beta-decay of 241Pu, was used as spike for the measurement of the amount content of 243Am by IDMS. An aliquot of about 2.5 g was taken out of each of the 18 units and mixed with an aliquot of about 1.0 g of the 241Pu spike solution.

Isotope ratios by TIMS

The isotope amount ratios n(241Am)/n(243Am) and n(242mAm)/n(243Am) of the unspiked material, sampled in aliquots of 0.7 g, were measured by thermal ionisation mass spectrometry. All isotope ratio measurements were performed using the total evaporation method on a multi-collector Triton TIMS [33].

Activity ratios by alpha spectrometry

High-resolution alpha particle spectrometry [34, 35] was used to determine the activity ratio A(243Am)/A(241Am). The set-up, which is often used for determining alpha-emission probabilities, has been described before [36]. The alpha source was prepared from the Am CRM solution by electrodeposition on a polished stainless steel disk with an active diameter of 18.6 mm. It was measured using passivated ion-implanted planar silicon detectors (PIPS®, Mirion Technologies (MGPI) SA, France).

For the production of the source, an 0.2 cm3 aliquot of the initial solution was transferred into a 100 cm3 glass beaker and evaporated to dryness. The residue was dissolved in 10 cm3 saturated ammonium nitrate (NH4NO3) solution (1920 g dm−3; T = 20 °C) and transferred into the electrodeposition cell. The beaker was rinsed with 2 cm3 portions of saturated NH4NO3 and finally with 2 cm3 of deionised water. The total volume of the electrolyte solution was approximately 16 cm3, having a pH = 3.0 (1). A mirror-polished stainless steel disk was used as source backing (cathode). A spirally wound platinum wire was used as anode and the cathode-to-anode distance was adjusted to approximately 7 mm. The electrodeposition current was kept stable at 0.85 (3) A at a voltage between 4.6 and 5 V over a period of 75 min. One minute before switching off the current, 1 cm3 of 25% ammonium hydroxide (NH4OH) was added to the solution to prevent the re-dissolution of the deposited americium layer. The source was rinsed with deionised water and dried at ambient temperature.

The source was measured at 3.6 cm source-to-detector distance using two PIPS® detectors of 150 mm2 and 300 mm2 active area. A magnet system on top of the source was used to deflect the conversion electrons away from the detector [37]. The intermediate spectra were acquired in daily cycles and shifted prior to summing into a composite spectrum, to compensate for any electronic gain drift during the measurement campaign [38, 39]. Three composite spectra were obtained and analysed with the deconvolution software 'BEST' [40]. The number of counts in the 241Am and 243Am peaks were between 3 × 106 and 2 × 107. As an example, the measured and fitted alpha-particle energy spectra obtained with the 300 mm2 PIPS® detector are shown in Fig. 2. The attained energy resolution was approximately 12.2 keV (FWHM) with the 150 mm2 detector and 15.8 keV (FWHM) with the 300 mm2 detector.

Fig. 2
figure 2

Measured (dots) and fitted (lines) alpha spectrum of the 243,241Am material, with interference peaks from 238Pu and tailing from other nuclides at higher energy (bottom). Residuals to the fit (top)

Full size image

Activity by alpha counting

The total Am activity per unit mass was determined by means of alpha-particle counting at a defined solid angle (DSA) [36, 41, 42]. This is potentially the most accurate primary standardisation technique for the activity of alpha-emitting nuclides [42]. By measuring a small fraction of alpha-particles emitted perpendicularly from the source plane, loss of particles by absorption in the source material at low emission angles is avoided. The detection efficiency practically equals the geometrical efficiency, which can be calculated from solid-angle formulas [43,44,45]. The accuracy of the method depends particularly on the reproducibility and accurate knowledge of the geometrical conditions. It is further improved by taking autoradiographs of the source activity, to tailor the solid-angle calculation to the radial activity distribution over the source area [42, 45].

Gravimetrically quantified drops of americium solution were deposited on 34-mm-diameter glass plates, with active areas of less than 19 mm diameter. They were dried on a heat plate at 110 °C and covered with 20 µg cm−2 VYNS foils (polyvinylchloride-polyvinylacetate copolymer) to prevent material loss. The sources were measured in two set-ups [36] with large passivated implanted planar silicon detectors of 3000 mm2 and 5000 mm2 surface area, at 5.7% and 6.7% geometrical efficiency (= solid angle/4π), respectively. The source-to-detector distances were accurately measured using both an optical focusing measuring device and a 3D coordinate measurement machine [46]. The energy threshold was set at approximately 1.5 MeV, thus avoiding detection of β-particles from the decay of 239Np. The total count rate ranged between 35 s−1 and 120 s−1, whereas the background rate was less than 0.03 s−1. Dedicated lifetime clock gates were used in combination with artificially imposed dead time [47]. The mean dead time was less than 0.07% and the cascade effect with pulse pileup [48] was insignificant (< 0.001%).

Analysis and results

Mass metrology

The mass metrology and mass spectrometry work performed in the frame of the characterisation of the americium reference material has been described elsewhere [16,17,18]. The resulting absolute amount contents and relative isotope fractions are provided in Table 1. The values are confirmed by an interlaboratory comparison organised by CEA/CETAMA using IRMM-0243/STAM as the test sample in the context of the certification of the 243Am spike [19].

Table 1 Measured amount contents and isotopic amount ratios in the reference material IRMM-0243 (243,241Am in 1 M HNO3 solution) measured by IDMS and TIMS [16,17,18,19] and their standard uncertainties at the reference date 1 January 2017
Full size table

Relative activity method

In the relative activity method, the half-life of 243Am is determined relatively to the half-life of 241Am, T1/2(241Am) = 432.6 (6) a [13], which is known with a relative standard uncertainty of 0.14%. From the definition of the decay constant follows a simple relationship for the 243Am/241Am half-life ratio

$$\frac{{T_{1/2}^{243} }}{{T_{1/2}^{241} }} = \frac{{\lambda_{241} }}{{\lambda_{243} }}{ = }\frac{{A_{241} }}{{A_{243} }}\frac{{N_{243} }}{{N_{241} }}$$
(1)

in which \(A_{241} /A_{243}\) represents the 241Am/243Am activity ratio and \(N_{243} /N_{241}\) the 243Am/241Am amount ratio in the americium material at the reference date. The amount ratio equals the mass fraction ratio divided by the atomic weight ratio.

The activity ratios derived from the three acquired alpha spectra are presented in Table 2. The number of counts C in the fitted peaks are corrected for decay during the measurement. The count rate is extrapolated to the reference date via the nuclide-specific \(f_{d}\) decay correction factor [1]

$$f_{d} = \frac{{\lambda t_{m} }}{{(1 - e^{{ - \lambda t_{m} }} )}}e^{{\lambda (t - t_{ref} )}}$$
(2)

in which \(t_{m}\) is the duration of the measurement, \((t - t_{ref} )\) is the time difference between the start of the measurement and the reference time, and \(\lambda\) is the decay constant of either 241Am or 243Am, such that the activity ratio at reference time is

$$\frac{{A_{241} }}{{A_{243} }} = \frac{{C_{241} }}{{C_{243} }}\frac{{f_{d}^{241} }}{{f_{d}^{243} }}$$
(3)
Table 2 Number of thousands of counts in the 241Am and 243Am peaks derived from the deconvolution of three composite alpha-particle spectra. Correction factors for decay (uncertainty < 0.001%), to convert count rates into activity at the reference date. Derived 241Am/243Am activity ratio and statistical uncertainty
Full size table

The ratios of the decay correction factors deviated by no more than 0.15% from unity, and their relative uncertainties were negligibly small.

As for the uncertainty estimate, besides the Poisson statistics governing the peak areas, there is an important uncertainty component to be considered from the tailing of the 241Am peak underneath the 243Am peak area. Wrong assessment of the tailing area leads to a fully correlated error in the nominator and the denominator of the activity ratio. The corresponding variance is propagated by a factor of 4, as explained in the case study I in Ref. [35]. To account for additional correlations, a model of the experiment was set up and the GUM Workbench software [49] was used to estimate the uncertainties for the counts \(C_{241}\), \(C_{243}\) and the relative activity \(A_{241} /A_{243}\), similar to the method used in Ref.[50]. It is compliant with the 'ISO Guide to the Expression of Uncertainty in Measurement' [51] and the requirement document EA 4/02 of the European Cooperation for Accreditation [52].

The spectrum was hypothetically divided into two energy regions, region ‘A’ [4700–5360] keV and region ‘B’ [5361–5580] keV, which mainly cover the 243Am and 241Am peak areas and contain \(C_{A}\) and \(C_{B}\) counts, respectively. The regions contain additional counts, \(C_{A,t}\) and \(C_{B,t}\), mainly originating from the tailing of other alpha emitters having peaks at higher energy, such as 244Cm and 242Cm. The area of the tailing part of the 241Am peak interfering in region A is denoted \(C_{B,A}\). The model equations to investigate the uncertainties on the Am peak areas \(C_{241}\) and \(C_{243}\) are

$$\left\{ {\begin{array}{*{20}c} {C_{243} = C_{A} - C_{A,t} + C_{A,f} \quad \;\;\quad } \\ {C_{241} = C_{B} - C_{B,t} + C_{B,A} + C_{B,f} } \\ \end{array} } \right.$$
(4)

Two additional components, \(C_{A,f}\) and \(C_{B,f}\), represent a measure for the goodness of the fit. Their nominal value is set equal to zero, but their uncertainty is taken as the sum of the absolute residuals, i.e. the difference between measurement and fit in each spectrum channel. For the other components, the square root of the number of counts is taken as the statistical uncertainty value. The mean activity ratio was determined as \(A_{241} /A_{243}\) = 2.313 (1) (see Table 1), and the half-life ratio \(T_{1/2}^{243} /T_{1/2}^{241}\) = 16.988 (24). With 0.14% relative standard uncertainty on the 241Am half-life as well as on the half-life ratio, the 243Am half-life was determined with 0.2% relative uncertainty as 7349 (15) a.

Specific activity method

By measuring the activity of the 243Am with an absolute method, the dependence on the 241Am half-life can in principle be eliminated. In this experiment, no pure 243Am material was available. Therefore, the total activity \(A_{tot} = A_{241} + A_{243}\) was measured and the contribution of 241Am was subtracted on the basis of the relative activity \(A_{241} /A_{243}\). Consequently, the measurement results of the absolute and relative methods in this work are correlated to some extent, so that the ‘absolute’ method de facto qualifies as a ‘hybrid’ method.

The measurement equation follows directly from \(A_{243} = \lambda_{243} N_{243}\)

$$T_{1/2}^{243} = \ln (2)\frac{{N_{243} }}{m}\frac{m}{{A_{tot} }}\left( {1 + \frac{{A_{241} }}{{A_{243} }}} \right)$$
(5)

in which \(N_{243} /m\) and \(A_{tot} /m\) are the number of 243Am atoms and the 241Am + 243Am activity per gram of solution, respectively.

The activity at the reference date, \(A_{tot} (t_{ref} )\) (Bq), is obtained by counting alpha particles under a small but well-defined solid angle, using the equation

$$A_{tot} = \frac{{C_{tot} }}{{t_{m} }}\frac{4\pi }{\Omega }f_{tail} f_{d}$$
(6)

in which \(C_{tot} /t_{m}\) is the number of counts per system live-time, which is adequately corrected for count loss through pileup and system dead time by imposing a well-known dead time for each registered pulse [47, 48]; \(\Omega\) is the solid angle in steradian [41, 43,44,45]; \(f_{tail}\) is a correction factor for the extrapolation of the spectrum below the imposed low-energy threshold [36]; and \(f_{d}\) is a weighted decay correction factor (Eq. 2) for both Am isotopes, based on the activity ratio derived from alpha spectrometry.

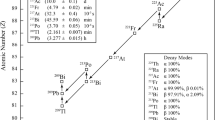
The total number of counts \(C_{tot}\) had to be corrected for the presence of radioactive impurities. In Fig. 3, decay schemes are shown for 241,243,242mAm and 244Cm, in view of their relevance to this part of the work. Interference from the decay products of 241,243Am is considered negligible. With high-resolution alpha-particle spectrometry (see relative method), alpha peaks from the decay of 244Cm and 242mAm were identified. Small alpha peaks from 238Pu fed through the decay of 242Cm could not be discerned because they were masked by the 241Am peaks. Assuming that the material was free from Pu at the last chemical purification on 28 April 2015 [16,17,18], the ingrowth of 238Pu was calculated as approximately 0.8% of the 242Cm activity at the reference date. The contribution of the impurities to the total activity was measured as 0.19 (2) %. This fraction is consistent with the value 0.21 (1) % derived from the interlaboratory comparison [19].

Fig. 3
figure 3

Decay chains of the main radionuclides present in the radioactive solution

Full size image

An overview of the uncertainty assessment of a typical activity measurement is presented in Table 3. Corrections for decay during the short measurement period \(t_{m}\) were insignificant. Half of the tailing correction \(f_{tail}\) is taken as its uncertainty. Backscattering effects of alpha-particles on the glass plate and self-absorption of the material are possible, but with less than 0.02% probability each, and are introduced into the uncertainty budget. The activity concentration values of the solution calculated via Eq. 6 for each source are presented in Table 4. All results were internally consistent.

Table 3 Typical standard uncertainty budget of the absolute activity concentration of the solution derived from measuring a
Full size table
Table 4 Total activity per gram of solution at reference date 1 January 2017 as calculated from the measurements of the individual sources standardised by alpha-particle counting at a defined solid angle. The relative standard uncertainty on the 243Am + 241Am activity is 0.16%
Full size table

With 0.16% relative standard uncertainty on the 241Am + 243Am activity per unit mass, 33.99 (6) Bq/g, and 0.14% on the activity ratio, 16.988 (24), the 243Am half-life was determined with 0.2% relative uncertainty as 7342 (14) a.

Discussion

The results from both methods agree extremely well, and their average value 7345 (14) a is taken as the final estimate of the 243Am half-life. There is significant correlation between the two methods, both relying on the measured activity ratio between the isotopes. Therefore, the uncertainty value of the more precise method was adopted directly to the mean half-life instead of the combined uncertainty, since a rigorous error propagation would not result in a significantly lower uncertainty. The results obtained in this work are consistent with literature values. An overview of published experimental half-life values is presented in Table 5 [13] and shown graphically in Fig. 4. The half-life ratio agrees within one combined standard uncertainty with the five other published data. Also the specific activity measurements are mutually compatible within one combined standard uncertainty. The uncertainties in this work are lower, mainly due to the more accurately performed alpha-particle counting and spectrometry measurements.

Table 5 Overview of measured 243Am half-life values, determined by specific activity or relative to the 241Am half-life (= 432.6 (6) a) and the recommended evaluated value by the DDEP [13]. Below are the half-life values obtained in this work and their mean value
Full size table
Fig. 4
figure 4

Comparison of previously measured 243Am half-life values (Table 5) with the ‘New’ result from this work and a recommended ‘Mean’ value calculated from the four most recent 243Am/241Am half-life ratios

Full size image

A power-moderated mean (PMM) with α = 1 – where the number α denotes the power of the uncertainties in the weighting factors [53] –of the three most recent (and consistent) half-life ratio data in Table 5 results in 17.011 (28) a. This is compatible with, but less precise than the value 16.988 (24) measured in this work, or the slightly lower value 16.980 (24) derived from the mean half-life result 7345 (14) a from both methods. The PMM (α = 2) of the latter with the three literature data yields 16.998 (17), which can be recommended as a good overall estimate. This ratio in combination with T1/2(241Am) = 432.6 (6) a leads to a recommended half-life value of T1/2(243Am) = 7353 (10) a.

Conclusions

The 243Am half-life and the 243Am/241Am half-life ratio have been measured accurately by combining mass spectrometry through IDMS and TIMS, high-resolution alpha-particle spectrometry, and alpha-particle counting measurements. The values derived from a mean of two methods, 7345 (14) a for the 243Am half-life and 16.980 (24) for the 243Am/241Am half-life ratio, have the smallest uncertainty hitherto reported, yet agree very well with published experimental work. In combination with three consistent literature data, and assuming that T1/2(241Am) = 432.6 (6) a, mean values of T1/2(243Am)/T1/2(241Am) = 16.998 (17) and T1/2(243Am) = 7353 (10) a can be recommended as good estimates.