On a Scaled Symmetric Dai–Liao-Type Scheme for Constrained System of Nonlinear Equations with Applications

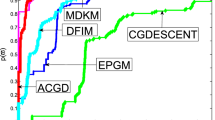
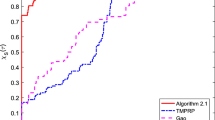
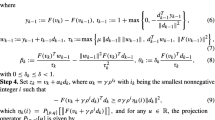Abstract

In this paper, a new Dai–Liao (DL)-type projection algorithm is presented for large-dimension nonlinear monotone problems with signal reconstruction and image recovery applications. The inspiration behind the work comes from two of the open problems propounded by Andrei (Bull Malays Math Sci Soc 34(2):319–330, 2011) involving the optimal value for the DL nonnegative parameter and the best conjugacy condition as well as the fine attributes expressed by four-term methods for unconstrained optimization. Based on the eigenvalue study of a symmetric DL-type iteration matrix, another optimal choice of the DL parameter is obtained, which is incorporated in a five-term direction scheme. Combining this with the projection method, a new DL algorithm which converges globally is developed. To implement the algorithm, a derivative-free line search mechanism is employed. Also, by conducting some numerical experiments with the new scheme and some recent DL-type methods, the efficiency of the former in solving nonlinear monotone problems as well as the $\ell _1-norm$ regularized problems in compressed sensing is demonstrated.

Appendix

The appendix contains six examples of the operator F, their dimensions, and six initial guesses.

The following are six examples of the operator F used in the experiment:

Example 1

Nonsmooth function obtained from [33].

$F_i(x)=2x_i-\sin {|x_i|}$, $\quad i=1,2, \dots ,n$,

where ${\mathcal {C}} ={\mathbb {R}}_+^n$.

Example 2

This is obtained from [57].

$F_1(x)= 2x_1+\sin {x_1}-1$,

$F_i(x)= -2x_{i-1}+2x_i+2\sin {x_i}-1$,

$F_n(x)=2x_n+\sin {x_n}-1$,$\quad i=2,\dots ,n-1$,

where ${\mathcal {C}} ={\mathbb {R}}_+^n$.

Example 3

Penalty function 1 obtained from [15].

$F_i(x)=2\pi (x_i-1)+4(\sum _{j=1}^{n}x_j-0.25)x_i, \quad i=1,2,\dots ,n$,

where $\pi =10^{-5}, \quad {\mathcal {C}} ={\mathbb {R}}_+^n$.

Example 4

Nonsmooth function [50].

$F_i(x)=x_i-\sin {|x_i-1|}$, $\quad i=1,2, \dots ,n$,

where ${\mathcal {C}} =\left\{ x\in {\mathbb {R}}^n:\displaystyle \sum _{i=1}^{n}x_i\le n, \quad x_i\ge -1, \quad i=1,2,\dots ,n\right\} .$

Example 5

This example is obtained from [2].

$F_1(x)=2.5x_1+x_2-1$,

$F_i(x)=x_{i-1}+2.5x_{i}+x_{i+1}-1$,

$F_n(x)=x_{n-1} + 2.5x_n-1, i=2,3,...,n-1$, where $\mathcal {C} =\mathbb {R}_+^n$

Example 6

Nonsmooth function obtained from [22].

$F_i(x)=2x_i-\sin {|x_i-1|}$, $\quad i=1,2, \dots ,n$,

where ${\mathcal {C}} =\left\{ x\in {\mathbb {R}}^n:\displaystyle \sum _{i=1}^{n}x_i\le n, \quad x_i\ge -1, \quad i=1,2,\dots ,n\right\}$.

A total of 18 experiments were conducted for each of the six examples of the operator F with dimensions $10^4$, $5\times 10^4$, $10^5$, and the following initial guesses:

$x_0^{1}$$=\left( \frac{1}{n},\frac{2}{n},...,1\right) ^T$, $x_0^{2}$ $=\left( \frac{3}{2},\frac{1}{2},...,-\frac{[(-1)^n-2]}{2}\right) ^T$, $x_0^{3}$ $=\left( \frac{1}{3},\frac{1}{3^2},...,\frac{1}{3^n}\right) ^T$,

$x_0^{4}$ $=\left( \frac{n-1}{n},\frac{n-2}{n},...,0\right) ^T$, $x_0^{5}$ $=\left( 3,1,...,-2\frac{[(-1)^n-2]}{2}\right) ^T$, $x_0^{6}$$=\left( 1-\frac{1}{n},1-\frac{2}{n},...,0\right) ^T$.