1 Introduction

A situation, in which a finite set of players can generate certain payoffs by cooperation, can be described by a cooperative game with transferable utility (or simply a TU-game). Such a game consists of a (finite) set of players and for every subset of this set of players, called coalition, a real number representing the worth that the players in this coalition can earn by cooperating. Depending on the application, players in a game can represent, for example, rational decision-making agents, political parties in a voting body, tasks to be served by a server, etc. In many applications, there is some structure on the player set. In the literature, such structures can be modeled by various combinatorial structures, such as ‘classic’ undirected graphs in Myerson [1] or directed graphs in Gilles et al. [2] or Faigle and Kern [3], but also more general structures such as antimatroids in Algaba et al. [4], convex geometries in Bilbao and Edelman [5], augmenting systems in Bilbao [6], regular set systems in Honda and Grabisch [7] and Lange and Grabisch [8] or union stable systems in Algaba et al. [9, 10]. In the underlying paper, we focus on games, where there is a hierarchical structure on the set of players. For example, consider a set of tasks, say tasks \(1,\ 2\) and 3, that have to be served on a server, such that there is some (partial) order by which the tasks must be served, say that task 1 cannot be started before another task 2 has been completed. Furthermore, when a given product has to be disassembled, often some components can be removed only after other components have previously been removed.

In order to model these kind of situations, cooperative TU-games are enriched with a directed graph on the set of players. Two approaches that are followed in the literature are the following. First, in the games with a permission structure, introduced by Gilles et al. [2], restrictions in coalition formation are modeled by a ‘set approach’ in the sense that from the digraph we derive a set of feasible coalitions, i.e., a subset of the power set of all players. The second approach is that of games under precedence constraints, introduced by Faigle and Kern [3] (see also Grabisch and Sudhölter [11, 12]) where, instead of restricting the set of feasible coalitions, one follows an ‘order approach’ and restricts the set of admissible orders in which coalitions form. In this paper, we follow the second approach. A game under a precedence constraint is a game, where the player set is endowed with a precedence relation, represented by a partial order (i.e., reflexive, antisymmetric and transitive relation) on the player set. Equivalently, it can be represented by an acyclic directed graph. Players enter to form the ‘grand coalition,’ consisting of all players according to some permutation on the player set. Given an acyclic digraph, a permutation of the players is called admissible, if players enter after their successors in the digraph. Consequently, a coalition of players is considered feasible, if for every player in the coalition, all of its successors in the digraph are also present in the coalition. The fact that the set of players is partially ordered by an acyclic digraph allows for enumerating all feasible subsets, which has important implications in problems for systems of tasks with this type of ordering constraints (see Skiena [13]).

A player is a null player in a game under precedence constraints, if its contribution to every admissible permutation is zero. A player is called irrelevant if it is a null player and all its superiors in the digraph are also null players. Irrelevant player independence is subsequently defined as the property that the payoff to relevant players (i.e., players that are not irrelevant) is not affected by the presence of irrelevant players. Since irrelevant players have no contribution in the game, nor are they needed to allow cooperation with any player who has a contribution in the game, we consider this a desirable property.

We introduce a new class of solutions for games under precedence constraints that satisfy irrelevant player independence. Using this independence axiom, we obtain axiomatizations of the solutions in this class by the well-known axioms of efficiency and linearity, and new axioms called irrelevant player property and p-strength. The irrelevant player property requires that irrelevant players earn a zero payoff. This is a considerable weakening of the null player property used by Faigle and Kern [3] (and [14], for a special case), which requires that every null player earns a zero payoff, and thus ignores the fact that null players might still have predecessors that are non-null players, but who need the presence of the null player. The irrelevant player property allows that null players still earn a nonzero payoff because of having the ability to make non-null players active. The p-strength axiom requires that in case we consider the unanimity game of the ‘grand coalition,’ consisting of all players, then the payoffs are allocated proportional to some power measure p. A power measure for acyclic digraphs is a function that assigns values to the players in an acyclic digraph that can be interpreted as the ‘strength’ or ‘influence’ of these players in the digraph. Besides using arbitrary power measures, this is a modification of the hierarchical strength axiom of Faigle and Kern [3] in the sense that they consider the unanimity game of any coalition. By considering only the unanimity game of the grand coalition, we only consider situations where all players are identical in the game, and therefore, the only difference is with respect to their position in the digraph. According to p-strength, the payoff allocation in the unanimity game, where all players are identical, is fully determined by the power measure p. The class of solutions that is characterized by the above axioms is what we call the class of precedence power solutions. For a positive power measure p, the corresponding p-hierarchical solution that is characterized by the above axioms is the solution that allocates the so-called Harsanyi dividends of any feasible coalition in a game over the players in that coalition, proportional to their power according to measure p.

Within the new class of precedence power solutions, we give special attention to the hierarchical solution, which is based on the hierarchical measure as power measure for acyclic digraphs, and compare it with the known precedence Shapley value of Faigle and Kern [3], which is not a precedence power solution since it does not satisfy independence of irrelevant players. However, other power measures from the literature can be applied, such as the ones given by Gould [15], White and Borgatti [16], the \(\beta \)-measure of van den Brink and Gilles [17] and its reflexive version in van den Brink and Borm [18], the \(\lambda \)-measure of Borm et al. [19], the positional power measure of Herings et al. [20] or the centrality measures in del Pozo et al. [21]. This also shows how social network theory and mathematical game theory are intertwined as soon as we consider network structures among players in a game. We end the paper with giving an axiomatization of the hierarchical measure as power measure.

After preliminaries in Sect. 2, we introduce and axiomatize the class of precedence power solutions in Sect. 3. In Sect. 4, we focus on the specific hierarchical solution and compare it with the precedence Shapley value. In Sect. 5, we characterize the hierarchical measure that underlies the hierarchical solution, before concluding in Sect. 6.

2 Preliminaries: Games Under Precedence Constraints

Precedence constraints are given by an acyclic digraph. An irreflexive directed graph or irreflexive digraph is a pair (N, D),  with N a finite set of positive integers whose elements are called nodes, and \(D\subseteq \{(i,j): i,j\in N,i\ne j\}\) is an (irreflexive) binary relation on N,  consisting of ordered pairs called arcs. Since the nodes will represent players, we often refer to the nodes as players. For \(i\in N\), the nodes in \(F_{D}(i):=\{j\in N: (i,j)\in D\}\) are called the followers or successors of i in D, and the nodes in \(P_{D}(i):=\{j\in N: (j,i)\in D\}\) are called the predecessors of i in D. Furthermore, we define the set of subordinates of i in D as the set \({\widehat{F}}_{D}(i)\) such that \( j\in {\widehat{F}}_{D}(i)\) iff there exists a sequence of players \( (h_{1},\ldots ,h_{t})\) with \(h_{1}=i\), \(h_{k+1}\in F_{D}(h_{k}),\) for all \( 1\le k\le t-1\), and \(h_{t}=j\). We refer to the players in the set \( {\widehat{P}}_{D}(i)=\{j\in N: i\in {\widehat{F}}_{D}(j)\}\) as i’s superiors. The digraph \(\left( N,D\right) \) is acyclic iff \(i\not \in {\widehat{F}}_{D}(i),\) for all \(i\in N\). We denote the collection of all acyclic digraphs by \({\mathcal {D}}\). By \({\text {TOP}}(N,D)=\{i\in N: P_{D}(i)=\emptyset \},\) we denote the set of top players in (N, D), i.e., the set of players without predecessors. Note that \({\text {TOP}}(N,D) \ne \emptyset \) if the digraph is acyclic.

Faigle and Kern [3] consider situations, where cooperation between players in a cooperative TU-game is restricted by a partial order on the player set, that can be represented by an acyclic digraph. A coalition is feasible iff for any player in the coalition all of its successors in the digraph are also present in the coalition. The set \(\varPhi ^{p}(N,D)\) of feasible coalitions, according to digraph \( (N,D)\in {\mathcal {D}},\) is thus given by

$$\begin{aligned} \varPhi ^{p}(N,D)=\{S\subseteq N: F_{D}(i)\subseteq S,\quad \text{ for } \text{ all }\quad i\in S\}. \end{aligned}$$
(1)

A permutation \(\pi :N\rightarrow N\) is admissible in acyclic digraph (N, D) iff \(\pi (i)>\pi (j)\) whenever \((i,j)\in D\), i.e., successors enter before their predecessors in the digraph. The set of admissible permutations \(\varPi _{D}(N)\) in D is

$$\begin{aligned} \varPi _{D}(N)=\{\pi :N\rightarrow N: \pi (i)>\pi (j)\quad \text{ if }\quad (i,j)\in D\}. \end{aligned}$$
(2)

A TU-game under precedence constraints is a triple (N, v, D), where N is a finite set of positive integers whose elements are called players, \((N,D)\in {\mathcal {D}}\) is an acyclic digraph and \(v:\varPhi ^{p}(N,D)\rightarrow \mathrm {IR }\) is a characteristic function (cooperative TU-game), that assigns to every set S in \(\varPhi ^{p}(N,D)\) a worth v(S), with \( v(\emptyset )=0\). The worth v(S) of coalition \(S \subseteq N\) is what the players in S can earn by cooperating. We denote the class of all games under precedence constraints by \({\mathcal {G}} _{PC}\). For \((N,v,D),(N,w,D)\in {\mathcal {G}}_{PC}\) and \(\alpha ,\beta \in {\mathrm {I R}}\), the game \((N,\alpha v+\beta w,D)\) is defined by \((\alpha v+\beta w)(S):=\alpha v(S)+\beta w(S)\) for \(S\in \varPhi ^{p}(N,D)\). For each \(T\in \varPhi ^{p}(N,D)\), \(T\ne \emptyset \), the unanimity game under precedence constraints \((N,u_{T},D)\in {\mathcal {G}}_{PC}\) is given by \(u_{T}(S)=1\) if \(T\subseteq S\), and \(u_{T}(S)=0,\) otherwise, \(S\in \varPhi ^{p}(N,D)\). For every \((N,v,D)\in {\mathcal {G}}_{PC}\), Faigle and Kern [3] show that the characteristic function in (N, v, D) can be written as

$$\begin{aligned} v=\sum _{T\in \varPhi ^{p}(N,D),\ T\ne \emptyset }\varDelta _{v}^{D}(T)u_{T}, \end{aligned}$$
(3)

with \(\varDelta _{v}^{D}(T)\) the dividend of \(S\in \varPhi ^{p}(N,D)\), recursively obtained according to the size of the feasible coalitions:

$$\begin{aligned} \varDelta _{v}^{D}(T)=v(T)-\sum _{H\subset T,H\in \varPhi ^{p}(N,D),H\ne \emptyset }\varDelta _{v}^{D}(H). \end{aligned}$$
(4)

Harsanyi [22] assumed that every coalition in a TU-game negotiates a vector of dividends such that the sum of all coalitions’ dividends vectors would be a feasible allocation for the grand coalition N. Therefore, the dividend of a coalition S is what is left after all proper subcoalitions of S have received their dividends. If \(\varPhi ^{p}(N,D) = 2^{N}\), then all notions as unanimity games and dividends boil down to the standard notions for cooperative TU-games. Finally, for \((N,v,D)\in {\mathcal {G}} _{PC}\) and \(S \in \varPhi ^p(N,D)\), the subgame \((S,v_{S},D(S))\), is given by \(v_{S}(T)=v(T),\) for all feasible coalitions \( T\subseteq S\), and \(D(S)=\{(i,j)\in D: \{i,j\}\subseteq S\}\).

3 Precedence Power Solutions

A power measure for acyclic digraphs is a function p that to every acyclic digraph \((N,D) \in {\mathcal {D}}\) assigns a vector \(p(N,D) \in { \mathbb {R}}^N\). For a player \(i \in N\), \(p_i(N,D)\) is a measure of its ‘power’ or ‘influence’ in (N, D). In this paper, we only consider positive power measures, meaning that \(\sum _{j\in N}p_{j}(N,D)>0,\) for all \((N,D) \in {\mathcal {D}}\). Let P be the collection of all positive power measures.

A solution for games under precedence constraints is a function f,  assigning to every game under precedence constraints \((N,v,D)\in {\mathcal {G}}_{PC}\) a real vector of n-components \(f(N,v,D) \in \mathbb {R}^N\), where each component represents the payoff assigned to each player. For positive power measure p, we define the p-hierarchical solution as the solution that allocates the dividend of a coalition \(S \in \varPhi ^p(N,D)\) among the players in S proportionally to p(S, D(S)).

Definition 3.1

For a positive power measure p, the p-hierarchical solution is the solution \(H^p\) on \(\mathcal{G}_{PC}\) given by

$$\begin{aligned} {H}^p_i(N,v,D) = \sum _{\mathop {i \in S}\limits ^{S \in \varPhi ^p(N,D)}} \frac{{p}_i(S,D(S))}{\sum _{j \in S} {p}_j(S,D(S))} \varDelta _v^D(S), \quad \text{ for } \text{ all }\quad i \in N. \end{aligned}$$

We refer to the class, consisting of all p-hierarchical solutions, as the class of precedence power solutions. To distinguish different solutions, and to motivate the use of a particular solution in an application, we follow the axiomatic approach. This means that we define several axioms or properties that are satisfied by a particular solution and only by this solution. If one accepts the axioms, then one should use the corresponding solution. Otherwise, one can identify which axiom is not desirable, which is much more helpful than just rejecting the whole solution. The first two axioms are straightforward adaptations of known axioms for TU-game solutions.

  • Efficiency For each game \((N,v,D) \in {\mathcal {G}}_{PC}, \sum _{i \in N} f_i(N,v,D) = v(N)\).

  • Linearity For every pair of games \((N,v,D), (N,w,D) \in {\mathcal {G}}_{PC}\) and \(\alpha , \beta \in {\mathbb {R}}\), it holds that \(f(N,\alpha v+\beta w,D) = \alpha f(N,v,D)+ \beta f(N,w,D)\).

For admissible permutation \(\pi \in \varPi _D(N)\) and player \(i \in N\), the precedence marginal vector \(m^{\pi }(N,v,D) \in { \mathbb {R}}^{N}\) is given by

$$\begin{aligned} m^{\pi }_i(N,v,D) = v(\{j \in N : \pi (j) \le \pi (i)\}) - v(\{j \in N : \pi (j) < \pi (i)\}). \end{aligned}$$
(5)

A player \(i \in N\) is a null player in game under precedence constraints (N, v, D), iff for every \(\pi \in \varPi _D(N)\) it holds that \( m^{\pi }_{i}(N,v,D)=0\). Player \(i \in N\) is an irrelevant player in (N, v, D) iff i is a null player, and every \(j \in {\widehat{P}}_D(i)\) is also a null player. A player \(i \in N\) is relevant if it is not an irrelevant player. The irrelevant player property requires that an irrelevant player earns a zero payoff.

  • Irrelevant player property For each \((N,v,D) \in {\mathcal {G}} _{PC}\), if \(i \in N\) is an irrelevant player in (N, v, D), then \(f_i(N,v,D)=0 \).

Let \({\text {Irr}}(N,v,D)\) be the set of irrelevant players in game under precedence constraints (N, v, D). For \({\mathcal {F}} \subseteq 2^N\), \(S \subseteq N\), let \({\mathcal {F}}_S = \{T \in {\mathcal {F}}: T \subseteq S\} \) be the collection of subsets of S in \({\mathcal {F}}\). Given \(N^{\prime }=N \setminus {\text {Irr}}(N,v,D)\), it holds that \(\varPhi ^p_{N^{\prime }}(N,D)=\varPhi ^p(N^{ \prime },D(N^{\prime }))\). This means that removing irrelevant players does not have an effect on the ability of relevant players to cooperate. Since irrelevant players are null players, they do not make any contribution to their subordinates in the digraph. Moreover, their superiors are also null players, and thus, an irrelevant player does not make any contribution either by letting other players that need them to be present in any feasible coalition in \(\varPhi ^{p}(N,D)\) cooperate. Since irrelevant players have no influence in creating value or by letting other players create value, we require that the removal of irrelevant players from the game does not affect the payoff to relevant players.

  • Irrelevant player independence Let \(N^{\prime }=N\setminus {\text {Irr}}(N,v,D)\). For every \((N,v,D)\in {\mathcal {G}}_{PC}\), it holds that \( f_{i}(N,v,D)=f_{i}(N^{\prime },v_{N^{\prime }},D(N^{\prime }))\) for \(i\in N^{\prime }\).

Finally, we introduce an axiom that reflects the power of the players in the digraph. In the unanimity game \((N,u_{N})\) on the grand coalition N, all players are equivalent with respect to the game since all players must agree to achieve a non-null worth. In that case, we require that the dividend allocation only depends on the strength of the players in the digraph, by assuming that the payoff allocation is proportional to some positive digraph power measure p.

  • p-strength For every \((N,D)\in {\mathcal {D}}\), positive power measure p and \(i,j\in N\), it holds that \(p_{i}(N,D)f_{j}(N,u_{N},D)=p_{j}(N,D)f_{i}(N,u_{N},D)\).

The p-hierarchical solution is axiomatized by the above four axioms. We first provide two lemmas.

Lemma 3.1

Let (N, v, D) be a game under precedence constraints. If coalition \(S \in \varPhi ^p(N,D)\) contains a player i who is a null player in (N, v, D),  and moreover \(S \subseteq N \setminus P_D(i)\), then \(\varDelta _{v}^D(S)=0\).

Proof

Consider a feasible coalition S,  containing null player i and no predecessors of i. Let \(H(S)= S \setminus {\widehat{F}}_D(i)\) be the set of players in S,  that are not subordinates of player i in D. By induction on |H(S)|, if \(|H(S)| = 0\), then the only feasible subset of S,  containing player i is S itself. Therefore, \(v(S)-v(S \setminus \{i\})=\varDelta _{v}^D(S)\). Since i is a null player in (N, v, D), it holds that \(v(S)-v(S \setminus \{i\})=0= \varDelta _{v}^D(S)\). Assume \(\varDelta _{v}^D(T)=0\), if \(0 \le |H(T)|<|H(S)|\). Since \(|H(S)|>0\), it holds that S is no longer the only feasible subset of S,  containing player i. Let \(K(S) = \{T\in \varPhi ^p(N,D): i \in T \text{ and } T \subset S\}\). It now holds that \(v(S)-v(S \setminus \{i\}) = \sum \nolimits _{T \in K(S)} \varDelta _{v}^D(T) + \varDelta _{v}^D(S)\). Since \(|H(T)|<|H(S)|\) for \(T \in K(S)\), by induction, we have \( \varDelta _{v}^D(T)=0,\) for all \(T \in K(S)\). Since i is a null player in (N, v, D), it holds that \(v(S)-v(S \setminus \{i\})=0=\varDelta _{v}^D(S)\). \(\square \)

Lemma 3.2

Let (N, v, D) be a game under precedence constraints. Player \(i \in N\) is an irrelevant player in game under precedence constraints (N, v, D) if and only if \(\varDelta _{v}^D(S)=0\) for every coalition \(S \in \varPhi ^p(N,D)\) with \(i \in S\).

Proof

  1. (i)

    To prove the ‘only if’ part, for \(S \subseteq N\), define \( P_D(S):=\bigcup _{i \in S} P_D(i)\). Let \(i \in N\) be an irrelevant player in (N, v, D). Let \(S \in \varPhi ^p(N,D)\) such that \(i \in S\). We show by induction on \(| {\widehat{P}}_D(i)|\) that \(\varDelta _{v}^D(S)=0\). If \(|{\widehat{P}}_D(i)| = 0\), then player i has no predecessors in (N, D). Let \(S \in \varPhi ^p(N,D)\) such that \(i \in S\). In this case, \(S \subseteq N = N \setminus P_D(i)\). Therefore, by Lemma 3.1, we have \(\varDelta _{v}^D(S)=0\). Proceeding by induction, assume that for every irrelevant player j such that \(|{\widehat{P}}_D(j)|<|{\widehat{P}}_D(i)|\) it holds that \( \varDelta _{v}^D(S)=0,\) for all coalitions \(S \in \varPhi ^p(N,D)\) with \(j \in S\). We already know that \(\varDelta _{v}^D(S)=0,\) for S such that \(S \cap {\widehat{P}}_D(i) \ne \emptyset \), by the fact that predecessors of irrelevant players are themselves also irrelevant and \(|{\widehat{P}}_D(j)|<|{\widehat{P}}_D(i)|,\) for any \(j \in {\widehat{P}}_D(i)\). Therefore, we only need to consider those feasible coalitions \(S\in \varPhi ^p(N,D),\) such that \(S \cap {\widehat{P}}_D(i) = \emptyset \). For these coalitions, it holds that \(S \subseteq N \setminus P_D(i)\). Hence, by Lemma 3.1, we have \(\varDelta _{v}^D(S)=0\).

  2. (ii)

    To prove the ‘if’ part, suppose that i is not an irrelevant player in (N, v, D). If i is not a null player in (N, v, D), then there exists \(S \in \varPhi ^p(N,D),\) with \(i \in S\), such that \(S \setminus \{i\}\in \varPhi ^p(N,D)\) and \(v(S)-v(S\setminus \{i\}) \ne 0\). We also have \(v(S)-v(S\setminus \{i\}) = \sum \nolimits _{T \subseteq S, i \in T, T \in \varPhi ^p(N,D)} \varDelta _{v}^D(T)\). It follows that there is at least one \(S \in \varPhi ^p(N,D), i \in S\), such that \(\varDelta _{v}^D(S) \ne 0\). If i is a null player, but there is a \(j \in {\widehat{P}}_D(i)\) that is not a null player, then we can reason in a similar way to obtain that there exists at least one \(S \in \varPhi ^p(N,D), j \in S\), such that \(\varDelta _{v}^D(S) \ne 0\). Since i is a subordinate of j, i must be in \(S \in \varPhi ^p(N,D)\).

\(\square \)

Next, the main theorem characterizes the precedence power solutions.

Theorem 3.1

Let p be a positive power measure. A solution for games under precedence constraints is equal to the p-hierarchical solution \(H^p\) if and only if it satisfies efficiency, linearity, the irrelevant player property, irrelevant player independence and p-strength.

Proof

It is straightforward to show that \(H^p\) satisfies efficiency, linearity, the irrelevant player property and p-strength. To show irrelevant player independence, consider game under precedence constraints (N, v, D) and precedence power solution \(H^p,\) obtained from power measure p. Let \( N^{\prime }=N \setminus {\text {Irr}}(N,v,D)\). By Lemma 3.2, it holds that \(\varDelta _v^D(S)=0\) if \(S \cap {\text {Irr}}(N,v,D) \ne \emptyset \), and from expression (4) of dividends, it follows that \( \varDelta _v^D(S) = \varDelta _{v_{N^{\prime }}}^D(S)\) for \(S \in \varPhi ^p_{N^{\prime }}(N,D)\).

For \(i \in N^{\prime }\), it holds that \(H^p_i(N,v,D) = \sum _{S \in \varPhi ^p(N,D), i \in S} \frac{p_i(S,D(S))}{\sum _{j \in S} p_j(S,D(S))} \varDelta _v^D(S).\)

Therefore, \(H^p_i(N,v,D)= \sum _{S \in \varPhi ^p_{(N^\prime ,D(N^\prime )}, i \in S} \frac{p_i(S,D(S))}{\sum _{j \in S} p_j(S,D(S))} \varDelta _{v^D_{N^{ \prime }}}(S)\). Moreover, \(H^p_i(N^{\prime },v_{N^{\prime }},D(N^{\prime })) = \sum _{S \in \varPhi ^p(N^{\prime },D(N^{\prime })), i \in S} \frac{p_i(S,D(N^{\prime })(S))}{ \sum _{j \in S} p_j(S,D(N^{\prime })(S))} \varDelta ^{D(N^{\prime })}_{v_{N^{ \prime }}}(S)\).

For all \(S \in \varPhi ^p(N^{\prime },D(N^{\prime })) = \varPhi ^p_{N^{\prime }}(N,D) := \{T \in \varPhi ^p(N,D) : T \subseteq N^{\prime }\} \) it holds \(D(S) = D(N^{\prime })(S)\), and thus, \(p_i(S,D(S)) = p_i(S,D(N^{\prime })(S)),\) for all \(i \in S\). Hence, we conclude that \( H^p_i(N,v,D) = H^p_i(N^{\prime },v_{N^{\prime }},D(N^{\prime }))\), showing irrelevant player independence.

To prove uniqueness, assume that solution f satisfies the axioms. Since f satisfies linearity, by (3) it is sufficient to consider uniqueness of f on unanimity games under precedence constraints. For unanimity game under precedence constraints \((N,u_S,D)\), \(S \in \varPhi ^p(N,D) \), the set of irrelevant players is given by \(N \setminus S\) (since \(S \in \varPhi ^p(N,D)\) implies \({\widehat{F}}_D(S) \subseteq S\)). Applying the irrelevant player property, these players are assigned zero payoff by f. By irrelevant player independence, for all \(i \in S\), it holds that \(f_i(N,u_S,D)=f_i(S,u_S,D)\).Footnote 1 Since \(u_S(S)=1\), from efficiency it follows that

$$\begin{aligned} \sum _{{k \in S}} f_k(S,u_S,D) = u_S(S)=1. \end{aligned}$$
(6)

Now consider any player \(i \in S\). If \(|S|=1\), then efficiency determines \( f_i(S,u_S,D)\). Therefore, suppose that \(|S| \ge 2\). Since \((S,u_S,D)\) is a unanimity game on the grand coalition S, we can apply p-strength to player i and any player \(k \in S \setminus \{i\}\) to obtain

$$\begin{aligned} p_i(S,D(S)) f_k(S,u_S,D) = p_k(S,D(S)) f_i(S,u_S,D). \end{aligned}$$
(7)

We distinguish the following two cases:

  1. (i)

    Suppose that \(p_i(S,D(S)) = 0\). Since \(\sum _{j \in S} p_j(S,D(S)) > 0\), there exists at least one \(k \in S \setminus \{i\}\) such that \(h_k(S,D(S)) \ne 0\). It follows from Eq. ( 7) applied to players i and k that \(f_i(S,u_S,D)=0\).

  2. (ii)

    Suppose that \(p_i(S,D(S)) > 0\). For \(k \in S \setminus \{i\}\), from Eq. (7) it follows

    $$\begin{aligned} f_k(S,u_S,D) = \frac{p_k(S,D(S))}{p_i(S,D(S))} f_i(S,u_S,D). \end{aligned}$$
    (8)

    By substituting this expression in Eq. (6), we obtain

    $$\begin{aligned} \sum _{{k \in S}} \frac{p_k(S,D(S))}{p_i(S,D(S))} f_i(S,u_S,D) = 1 \end{aligned}$$
    (9)

    As \(p_k(S,D(S))\) is known for \(k \in S\), \(f_i(S,u_S,D)\) is uniquely determined. \(\square \)

We remark that the axioms are logically independent. Examples, showing logical independence, can be obtained from the authors on request.

4 A Special Case: The Hierarchical Solution

Consider a game under precedence constraints \(\left( N,v,D\right) \). For \( i\in N,\) let

$$\begin{aligned} \varPi _{D}^{i}(N)=\{\pi \in \varPi _{D}(N): \pi (i)>\pi (j),\quad \text{ for } \text{ all }\quad j\in N\setminus \{i\}\}, \end{aligned}$$
(10)

be the collection of those permutations in \(\varPi _{D}(N),\) where i enters after all other players in \(N\setminus \{i\}\). Consider the power measure that assigns to every player the number of admissible permutations of N,  where it is the last player to enter.

Definition 4.1

The hierarchical measure \({\eta }\) is the power measure on \(\mathcal{D}\) given by \({\eta }_i(N,D)=|\varPi _D^i(N)|, \quad \text{ for } \text{ all }\quad i \in N.\)

We analyze this measure in the next section. Here, we apply it to define and characterize the specific precedence power solution that is obtained by taking the hierarchical measure as power measure in Definition 3.1 and Theorem 3.1.

Definition 4.2

The hierarchical solution \(H^\eta \) is the solution on \(\mathcal{G}_{PC}\) given by

$$\begin{aligned} {H^\eta _i}(N,v,D) = \sum _{\mathop {i \in S}\limits ^{S \in \varPhi ^p(N,D)}} \frac{{\eta }_i(S,D(S))}{\sum _{j \in S} {\eta }_j(S,D(S))} \varDelta _v^D(S),\ i \in N. \end{aligned}$$
(11)

Next, we compare this hierarchical solution with the known precedence Shapley value of Faigle and Kern [3]. For a game under precedence constraints \(\left( N,v,D\right) \), and \( i\in S, S\in \varPhi ^{p}(N,D)\), let

$$\begin{aligned} \varPi _{D}^{i}(N,S)=\{\pi \in \varPi _{D}(N): \pi (i)>\pi (j),\quad \text{ for } \text{ all }\quad j\in S\setminus \{i\}\}, \end{aligned}$$
(12)

be the collection of those permutations in \(\varPi _{D}(N),\) where i enters after the players in \(S\setminus \{i\}\). Note that \(\varPi _D^i(N) = \varPi _D^i(N,N)\) in case \(N=S\). The (absolute) hierarchical strength is the function h that assigns to every \((N,D)\in {\mathcal {D}}\) and coalition \(S\in \varPhi ^{p}(N,D)\) the vector \(h(N,D,S)\in { \mathrm {IR}}^{S}\), where \(h_{i}(N,D,S)\) is equal to \(|\varPi _{D}^{i}(N,S)|\), i.e., the number of permutations in \(\varPi _{D}(N),\) where \(i\in S\) enters after the players in \(S\setminus \{i\}\). Note that this is not a power measure as defined in Sect. 3 since the ‘power’ of a node also depends on the subset of the player set, which we are considering.

Whereas the hierarchical solution allocates the dividend of a feasible coalition, \(S\in \varPhi ^{p}(N,D)\), proportionally to the hierarchical measure \(\eta _{i}(S,D(S) )\), the precedence Shapley value applies the hierarchical strength \(h\left( N,D,S\right) \)

$$\begin{aligned} H_{i}\left( N,v,D\right) =\sum _{\begin{array}{c} S\in \varPhi ^{p}(N,D) \\ i\in S \end{array}} \frac{h_{i}\left( N,D,S\right) }{\sum _{j\in S}h_{j}\left( N,D,S\right) } \varDelta _{v}^{D}(S), \text{ for } \text{ all }\quad i\in N. \end{aligned}$$
(13)

Since the Shapley value for TU-games [23] allocates the Harsanyi dividends [22] equally over all players, in the corresponding coalition, when \(D=\emptyset \) (and thus, \(\varPhi ^p(N,D)=2^N\)), both the precedence Shapley value and the hierarchical solution assign the classical Shapley value. However, the precedence Shapley value is not a precedence power solution. This can be seen from the fact that it does not satisfy irrelevant player independence, as illustrated by the following example, which also illustrates the difference between the precedence Shapley value and the hierarchical solution.

Example 4.1

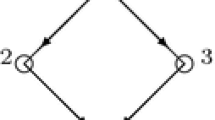
Consider a set of four tasks, which have to be performed in a certain (partial) order. The payoff to a coalition is one when at least tasks 1, 2 and 4 are completed and zero, otherwise. If tasks could be completed in any order, then the digraph that describes the order in which the tasks must be performed would be the empty set and, in that case, the hierarchical solution and the precedence Shapley value would be equal to the Shapley value, assigning \(\left( \frac{1}{3},\frac{1}{3},0,\frac{1}{3}\right) ,\) in this example. But now, suppose that task 1 has to be completed before task 3 and task 2 before tasks 3 and 4. This situation can be represented by the game under precedence constraints \( \left( N,v,D\right) , \) where \(N=\left\{ 1,2,3,4\right\} ,\) \(v=u_{\left\{ 1,2,4\right\} }\) and \(D=\left\{ \left( 3,1\right) ,\left( 3,2\right) ,\left( 4,2\right) \right\} \). The dividends of v are given by \(\varDelta _{v}^{D}\left( \left\{ 1,2,4\right\} \right) =1\) and \(\varDelta _{v}^{D}(S) =0,\) otherwise. The set of admissible permutations is

$$\begin{aligned} \varPi _{D}\left( N\right) =\left\{ \left( 1,2,3,4\right) ,\left( 1,2,4,3\right) ,\left( 2,1,3,4\right) ,\left( 2,1,4,3\right) , \left( 2,4,1,3\right) \right\} . \end{aligned}$$

For \( S=\left\{ 1,2,4\right\} \in \varPhi ^{p}(N,D)\), we get \( h_{1}\left( N,D,S\right) =1, h_{2}\left( N,D,S\right) =0\) and \(h_{4}\left( N,D,S\right) =4\), and, in this case, the precedence Shapley value is given by \( H\left( N,v,D\right) =\left( \frac{1}{5},0,0,\frac{4}{5}\right) \).

The set of admissible permutations in subgraph (S, D(S) ) is

$$\begin{aligned} \varPi _{D(S)}(S) =\left\{ \left( 1,2,4\right) ,\left( 2,1,4\right) ,\left( 2,4,1\right) \right\} . \end{aligned}$$
(14)

Therefore, \( \eta _{1}\left( S,D(S)\right) =1, \eta _{2}\left( S,D(S)\right) =0, \) and \( \eta _{4}\left( S,D(S)\right) =2,\) yielding the hierarchical solution \(H^\eta \left( N,v,D\right) =\left( \frac{1}{3},0,0,\frac{2}{3}\right) \) (Fig. 1).

Fig. 1
figure 1

Digraphs (N, D) and (S, D(S))

Full size image

Player 3 is an irrelevant player. Deleting player 3 yields game under precedence constraint \((N^\prime , v^\prime , D^\prime )\) with \( N^\prime =\{1,2,4\},\ v^\prime =u_{\{1,2,4\}}\) and \(D^\prime =\{(4,2)\}\). Then, the dividends of \(v^\prime \) are given by \(\varDelta _{v^\prime }^{D^\prime } \left( \left\{ 1,2,4\right\} \right) =1\) and \(\varDelta _{v^\prime }^{D^\prime }(S) =0,\) otherwise. Since \(N^\prime = S\), the set of admissible permutations \(\varPi _D(S)\) is given by (14): \( \varPi _{D}\left( N^\prime \right) = \varPi _D(S) = \left\{ \left( 1,2,4\right) ,\left( 2,1,4\right) ,\left( 2,4,1\right) \right\} . \) Hence, for \(S=N^\prime \in \varPhi ^{p}(N,D)\), we have \( h_{1}\left( N^\prime ,D^\prime ,S\right) =1, h_{2}\left( N^\prime ,D^\prime ,S\right) =0\) and \( h_{4}\left( N^\prime ,D^\prime ,S\right) =2\). Therefore, the presence of irrelevant player 3 has an effect on the payoff allocation for the precedence Shapley value. Obviously, in the case of the hierarchical solution, the payoffs are not influenced by the presence of player 3 since \(\eta (S,D(S))\) is the same as before. \(\square \)

Faigle and Kern [3] give an axiomatization of the precedence Shapley value, using efficiency, linearity, and the following two axioms.

  • Null player property For each \((N,v,D)\in {\mathcal {G}}_{PC}\), if \(i\in N\) is a null player in (N, v, D), then \(f_{i}(N,v,D)=0\).

  • Hierarchical strength Footnote 2 For every \((N,D)\in {\mathcal {D}}, S\in \varPhi ^{p}(N,D)\) and \(i,j\in S\), it holds that \(h_{i}(N,D,S)f_{j}(N,u_{S},D)=h_{j}(N,D,S)f_{i}(N,u_{S},D)\).

Theorem 4.1

(Faigle and Kern [3]) A solution for games under precedence constraints is equal to the precedence Shapley value H if and only if it satisfies efficiency, linearity, the null player property and hierarchical strength.

Notice that the null player property is stronger than the irrelevant player property since irrelevant players are null players, but not every null player is an irrelevant player. Further, the hierarchical strength h(N, D, S) is defined for every coalition S relative to the player set N. This is a main difference with p-strength, specifically \(\eta \)-strength, which only considers the unanimity game of the ‘grand coalition’ N, while hierarchical strength considers the unanimity game of any coalition. In the unanimity game of the ‘grand coalition’ N, all the players are symmetric, and therefore, a difference in payoffs assigned to different players must come from different digraph positions. However, when considering the unanimity game of a proper subcoalition of N, there might be also asymmetries between the players in the unanimity coalition with respect to their relation with null and non-null players. So, p-strength (specifically \(\eta \)-strength) is more appealing than hierarchical strength. Using these weaker and more appealing properties comes at a ‘price,’ namely that we need one axiom more. However, this axiom is irrelevant player independence, which we consider a desirable axiom, and hence an advantage of the hierarchical solution with respect to the precedence Shapley value, which does not satisfy it.

5 An Axiomatization of the Hierarchical Measure

Faigle and Kern [3] use the hierarchical strength as a tool to axiomatize the precedence Shapley value H. In the previous section, we saw that the hierarchical measure is a related power measure that underlies the hierarchical solution. To provide a deeper insight in the hierarchical measure \({ \eta }\), we give an axiomatization of this power measure on the class of acyclic digraphs. Therefore, we introduce several axioms that can be satisfied by a generic power measure p for acyclic digraphs.

The first axiom, 1-normalization, states that if digraph (N, D) contains only one player, then this player has power one.

  • 1-Normalization For \((N,D)\in {\mathcal {D}}\) with \(N=\{i\}, p_{i}(N,D)=1\).

The second axiom, the non-top property, states that players that are not top players in the graph have zero power. The digraph is interpreted as a hierarchical structure, where the only players that can enter as last player, and therefore are not depending on players that always enter after them, are players without predecessors.

  • Non-top property For every \((N,D)\in {\mathcal {D}}\) and \(i\in N\) such that \(P_{D}(i)\ne \emptyset \), it holds that \(p_{i}(N,D)=0\).

The third axiom is independence of successors and states that the power of a player does not depend on its successors. For a player \(i\in N\), the set of outgoing arcs from i is given by the set \(out_{D}(i):=\{(k,l)\in D: k=i\}\).

  • Independence of successors For every \((N,D)\in {\mathcal {D}}\) and each player \(i\in N,\) it holds that \(p_{i}(N,D)=p_{i}(N,D\setminus out_{D}(i))\).

Finally, the isolated player property states that the power of an isolated player (i.e., a player having no successors or predecessors) is equal to the sum of the powers of all other players in the subgraph without this isolated player. As isolated players neither have successors nor predecessors, these players might be considered to interact freely with any of the other players in the digraph. The isolated player property reflects that the power of an isolated player depends on the combined strength of the relations it is able to have with any of the other players, where the strength of each relation depends on the powers of the other players in the subgraph without the isolated player.

  • Isolated player property For every \((N,D)\in {\mathcal {D}}\) and \(i\in N\) such that \(F_{D}(i)\cup P_{D}(i)=\emptyset \), it holds that \( p_{i}(N,D)=\sum _{j\in N\setminus \{i\}}p_{j}(N\setminus \{i\},D_{-i})\).

The four previous axioms characterize the hierarchical measure. Examples, showing logical independence of the axioms, can be obtained from the authors on request.

Theorem 5.1

A power measure for acyclic digraphs is equal to the hierarchical measure \({\eta }\) if and only if it satisfies 1-normalization, the non-top property, independence of successors and the isolated player property.

Proof

Consider acyclic digraph (N, D). Since the only permutation on \(N=\{i\}\) is (i), it follows that hierarchical measure \({\eta }\) satisfies 1-normalization.

Since \(j\in P_{D}(i)\) implies that \(\pi (i)<\pi (j),\) for all \( \pi \in \varPi _{D}(N)\), there is no \(\pi \in \varPi _{D}(N)\) such that \(\pi (i)=n\) , and therefore, \({\eta }_{i}(N,D)=0\), showing that \({\eta }\) satisfies the non-top property.

Suppose that \(j\in F_{D}(i)\). Since conditions \(\varPi _{D}(N)\subset \varPi _{D\setminus \{(i,j)\}}(N)\) and \(\pi \in \varPi _{D\setminus \{(i,j)\}}(N)\setminus \varPi _{D}(N)\) imply that \(\pi (j)>\pi (i)\), then, we conclude that \({\eta }_{i}(N,D)={ \eta }_{i}(N,D\setminus \{(i,j)\})\). Repeated application for all arcs in \( out_{D}(i)\) shows that \({\eta }\) satisfies independence of successors.

For an isolated player \(i\in N,\) there does not exist \(j\in N\setminus \{i\}\) such that \((i,j)\in D\) or \((j,i)\in D\). It therefore holds that \(\pi \in \varPi _{D}(N)\) if and only if \(\pi _{N\setminus \{i\}}\in \varPi _{D_{-i}}(N\setminus \{i\})\). The number of admissible permutations in \(\varPi _{D}^{i}(N)\) is therefore equal to the number of possible relative orders \(\pi _{N\setminus \{i\}}\) of the players in \( N\setminus \{i\}\). It follows that \(|\varPi _{D}^{i}(N)|=|\varPi _{D_{-i}}(N\setminus \{i\})|\). Applying the definition of the hierarchical measure, it holds \(|\varPi _{D_{-i}}(N\setminus \{i\})|=\sum _{j\in N\setminus \{i\}}{\eta }_{j}(N\setminus \{i\},D_{-i})\). Then, \({\eta }_{i}(N,D)=|\varPi _{D}^{i}(N)|=|\varPi _{D_{-i}}(N\setminus \{i\})|=\sum _{j\in N\setminus \{i\}}{\eta }_{j}(N\setminus \{i\},D_{-i}),\) showing that \({\eta }\) satisfies the isolated player property.

To prove uniqueness, let p be a positive power measure, satisfying the axioms. We perform induction on |N|. If \(|N|=1 \), then \(p_{i}(\{i\},D)=1\) by 1-normalization. Proceeding by induction, assume that \(p(N^{\prime },D^{\prime })\) is uniquely determined if \( |N^{\prime }|<|N|\), and consider \((N,D)\in {\mathcal {D}}\). If \(P_{D}(i)\ne \emptyset , \) then it holds \(f_{i}(N,D)=0\) by the non-top property. Suppose that \(P_{D}(i)=\emptyset \). By independence of successors, \(p_{i}(N,D)=p_{i}(N,D\setminus out_{D}(i))\), and therefore, \(p_{i}(N,D)=p_{i}(N,D_{-i})=\sum _{j\in N\setminus \{i\}}p_{j}(N\setminus \{i\},D_{-i})\), where the last equality follows from the isolated player property. By the induction hypothesis, \(p_{j}(N\setminus \{i\},D_{-i}),\ j\in N\setminus \{i\}\), are known, and thus, \(p_{i}(N,D)\) is uniquely determined. \(\square \)

6 Conclusions

In the literature, the Shapley value has been extended to games associated with combinatorial structures more general than a digraph. For example, Algaba et al. [24] consider it in games on antimatroids, Bilbao and Edelman [5] studied it on convex geometries, and Bilbao and Ordoñez [25] and Algaba et al. [26] on augmenting systems. Convex geometries and augmenting systems have been shown to be contained in the class of so-called regular set systems considered by Honda and Grabisch [7] and Lange and Grabisch [8], who also consider an extension of the precedence Shapley value to games on regular set systems. We can use the ‘maximal chains’ in the definition of a regular set system to extend the hierarchical measure to this class.

Besides these generalizations, we can apply precedence power solutions to several applications of games on acyclic digraph structures. Two important applications concern the allocation of clean river water. The river games of Ambec and Sprumont [27] consider the problem of allocating clean water among the agents (countries), living along the river. On the other hand, Dong et al. [28] consider the cost allocation problem, where cleaning costs to clean a river from its pollution have to be allocated over the agents along the river. Applying precedence power solutions, we can consider different allocation rules, where the different power measures, on which the solutions are based, express the right of the agents on clean water (in case of allocating clean river water) or the responsibility of the agents in the pollution (in case of allocating cleaning costs). In allocating pollution cleaning costs over agents based on responsibility, the identification of contamination as studied by Gugat [29] is useful.