1 Introduction

Public services have traditionally been delivered by the public sector, e.g. national, regional or local governments. Historically, these public services took many forms including infrastructure projects and, in some cases, supply of necessity goods by state-owned companies. Increasing concerns about the levels of public debt along with a lack of effective and efficient management of these state-owned companies have led to an important movement of privatization of these state-owned companies in the 1980s championed by the UK [1, 2] and the USA [3]. Advocates of this movement often invoke the advantages of market mechanisms to justify this shift in public sector management—although very often “balancing the books” was the main motivation. For good surveys and books on privatization, the reader is referred to [4, 5]. Later on, additional factors led to the design and implementation of the concept of public–private partnerships (PPPs) such as knowledge-intensive technologies, unprecedented levels of public debts, poor public services and more demanding citizens.

Formally, a PPP project is a business agreement between the public sector and the private sector to deliver a public service by jointly assuming, to varying extents, financial, technical and operational risks, where the public sector stakeholders typically consist of national, regional and/or local governments, governmental agencies and state-owned entities, whereas the private sector stakeholders typically consist of private sub-contractors, private investors, financiers and insurers. In practice, these stakeholders are brought together under a legal entity or organizational framework known as the special purpose vehicle (SPV). The sharing of the costs of public services delivered by means of PPP projects varies over a continuum ranging from fully assumed by the public sector or taxpayers’ money, at one extreme, to fully assumed by the private sector or investors’ money, at the other extreme, depending on the type of agreement or contract, which is intimately related to the type of PPP project and the type of PPP model. In general, PPP projects are divided into two broad categories depending on whether their output is a public service for industry users or household users—these categories of PPP projects are often referred to as economic infrastructure projects and social infrastructure projects, respectively [6]. These categories could be further divided into two sub-categories depending on whether the project infrastructure is hard or soft, where hard infrastructures refer to transportation infrastructures (e.g. roads, highways, railways, bridges, ports, airports, public transport), utility infrastructures (e.g. electricity and gas production, transmission and distribution; water storage, treatment and distribution; sewerage and drainage network; industrial and household garbage collection, disposal and/or processing), telecommunication infrastructures (e.g. landline and mobile telephone networks, internet networks) and energy infrastructures (e.g. power generation and supply), whereas soft infrastructures refer to education infrastructures (e.g. schools and universities, libraries, vocational training centres, technology transfer agencies), healthcare infrastructures (e.g. hospitals, child care, aged care homes), social infrastructures (e.g. social security system; a range of community services such as housing, prisons and detention centres), leisure and tourism infrastructures (e.g. theatres, museums, parks), environmental infrastructures (e.g. environmental agencies), etc. On the other hand, PPP models are typically classified into five categories, namely supply and management model; turnkey model; lease model; concession model; and private ownership model [7], where the supply and management model consists of subcontracting the management of a project, an activity, or a public entity to the private sector; the turnkey model consists of subcontracting the realization of a project (e.g. construction of a hard infrastructure project) to the private sector; the lease model consists of subcontracting the operational management of a project to the private sector; the concession model consists of granting specific rights to the private sector for building and operating a project for a fixed period of time; and the private ownership model consists of using the private finance initiative (PFI) type of funding to design, construct and operate a project by the private sector from which the public sector purchases services. Furthermore, contracts could be divided into several categories depending on the choice of the subset of activities, around which the contract terms evolve, among the following: finance; design; build or rehabilitate or modernize or extend; transfer or lease or own; and operate. Well-known examples of contract designs in PPPs are build–operate–transfer (BOT) contracts and build–lease–transfer (BLT) contracts—for more variety of contract designs and case studies, the reader is referred to [8, 9].

The concept of public–private partnerships has attracted worldwide attention and acquired a new resonance in the context of developed and developing countries. PPPs are increasingly heralded as an innovative policy tool for remedying the lack of dynamism in traditional public service delivery. Several types of analyses have been proposed to address PPP projects including multi-criteria decision analysisFootnote 1 (e.g. [10]) and game theory. A game theory-based analysis models a PPP project as a game, where the players are often divided into two main categories, namely the public sector player(s) and the private sector players. To the best of our knowledge, contributions within this analysis framework make use of the Cardinal game theory modelling framework to analyse various decisions in PPP projects. To be more specific, the various decisions in PPP projects that have been addressed so far include bidding price [11], bid compensation for projects with costly bid preparation [12]; concession period—also referred to as stipend or honorarium [13–15]; costs and benefits allocation [16], risk sharing and allocation [17]; resource pricing and allocation [18], resource value increment allocation [19], royalties and subsidies negotiation [20], negotiation of changes in output-based specifications [21] and claims, financial renegotiations, and opportunistic behaviour [22–24]. To be the best of our knowledge, so far the decision problem concerned with the selection of the private sector partners has not been addressed yet within a game theory framework, although—at least conceptually—game theory is the most suitable analysis and solution framework as, by design, it allows one to take account of both the public sector perspective and the public sector perspective, and hence, it provides a more realistic solution for implementation. The importance of this problem and the proposed contribution of this paper lies in the consequences of a wrong choice of a private sector partner such as higher costs of realization of the project and further renegotiations, on the one hand, and the lack of more appropriate decision support systems, which take account of both the public sector and the private sector perspectives, to assist with the analysis of proposals and decision-making, on the other hand.

Our survey of the literature revealed that the common assumption made by researchers in this area is that stakeholders have well-defined payoff functions with respect to the key decision variables in PPP games, and thus, researchers have focused exclusively on Cardinal game theory type of analysis. In sum, our survey on cardinal game theory for PPPs highlights two shortcomings to the current published literature. First, in very many types of applications including PPPs, the specification of a cardinal payoff function is either infeasible or inappropriate. To be more specific, very often, the specification of a cardinal payoff function—also referred to as a utility function—requires the analyst to adopt simplifying assumptions with respect to the behaviour of players or the relationships between different decision variables. In practice, however, stakeholders may not be able to represent their preferences with payoff functions, especially under multiple criteria, but they may still be able to rank, with respect to multiple performance criteria or contractual terms, the alternatives they face from best to worst, which makes ordinal game theory type of analysis an alternative methodology for PPP projects. Second, most of the literature made a limited use of the potential of game theory as a modelling and analysis framework of PPPs in that only a limited number of decision variables relevant to most decision environments have been considered. In this research, we intend to fill these two gaps by providing an alternative framework, namely an ordinal game theory framework to analyse competitive bidding between private sector potential stakeholders for winning a PPP contract under multiple contractual terms or performance criteria related to these contractual terms. To be more specific, we provide a general ordinal game theory-based framework for analysing multiple contractual terms-based proposals in PPP projects along with an algorithm for the identification of the equilibrium or, equivalently, for predicting the contest’s winner. In sum, the proposed algorithm is a tool to assist with the selection of the private sector player to award the PPP contract to or the private sector players to shortlist for further negotiation. The main attractive features of the proposed algorithm could be summarized as follows: (1) it can handle any number of private sector players and any number of contractual terms and related performance criteria, (2) it determines a single ranking of proposals or bidders that take account of multiple performance criteria and reflects both the public sector perspective and the private sector perspective—as represented by their preference systems, (3) it can be used by the private sector players to analyse any set of potential proposals most likely to be submitted by bidders and to assist with the choice of bidding strategies, and (4) it can be used by the public sector player to analyse any set of potential proposals most likely to be submitted under any set of contractual terms and to assist with the choice of a realistic set of contractual terms and their performance measures. Note that, to the best of our knowledge, the only papers on ordinal game theory with methodological contributions are the ones by Cruz and Simaan [25], Xu [26] and Durieu et al. [27]. In the next section, we propose an ordinal game theory-based analysis framework for PPPs along with a new algorithm for its operationalization. As compared to the ordinal game theory frameworks proposed by Cruz and Simaan [25] and Xu [26], our framework is more general in that it can model games with any finite number of players, whereas [25] only considers two players and [26] considers the cases of two and three players, respectively. As to [27], they present a general model with any finite number of players, but they do not provide an algorithm for finding equilibria as we do in this paper. Also, to the best of our knowledge, this is the first paper to propose an ordinal game theory framework for the selection of private sector partners in PPP projects.

The remainder of this paper is organized as follows. In Sect. 2, we propose an ordinal game theory-based framework for selecting private sector partner(s) in PPPs and provide the means for its operationalization, namely an algorithm for finding an ordinal Nash equilibrium. We also provide relevant PPP-related concepts and tools. In Sect. 3, we analyse a typical scenario and use it to illustrate and discuss how the proposed methodology works. Finally, Sect. 4 concludes the paper.

2 General Framework and Analysis

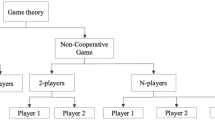
In this section, we propose an ordinal game theory-based framework for analysing competitive bidding between private sector potential partners for winning a PPP contract and provide the means for its operationalization, namely an algorithm for finding an ordinal non-cooperative equilibrium or, equivalently, for predicting the contest’s winner. We also provide the relevant PPP-related concepts and tools required for operationalizing the proposed framework. In sum, the proposed framework models a PPP project as an ordinal game between a public sector representative or player (e.g. a city council) and several private sector players, that is, private sector entities bidding for a PPP project, say \(P_1, {\ldots }, P_N \). For modelling purposes, we shall assume that the PPP project is fully described by means of a set of K contract terms and that the measures of the performance criteria used to assess the quality of any proposal on such terms are specified by the public sector representative. To comply with a common practice, we assume that each private sector player \(P_i \; (i:=1,\ldots ,N)\) submits a single proposal, say \(x^{i}:=\left( {x_1^i ,\ldots ,x_K^i } \right) \), to the public sector representative as part of the bidding process, where proposals are represented by vectors belonging to the K-dimensional Euclidean space \(IR^{K}\). Let \(X_i :=\left\{ {x_j^i :=\left( {x_{1,j}^i ,\ldots ,x_{K,j}^i } \right) ;j:=1\ldots ,M_i } \right\} \) denotes the set of potential proposals used by \(P_i \) \((i:=1,\ldots ,N)\) for analysis purposes, where \(M_i \) denotes the cardinality of \(X_i \). Formally, we model a PPP project as a static non-cooperative ordinal game of complete information among the private sector players, where private sector players’ strategies are the proposals they submit to the public sector representative. Note that, from a modelling perspective, the public sector representative is not formally modelled as a player in our game, as its actions depend purely on the proposals of the private sector players; that is, the public sector representative simply ranks the private sector bidders based on their proposals and selects the best one. Therefore, we shall refer to the public sector representative as a “silent” player. Nonetheless, the outcome of the game is based on the public sector representative’s preferences as reflected in the ranking of the private sector players’ proposals.

In the remainder of this section, we shall denote by X the Cartesian product of \(X_i \)s, that is, \(X:=\prod _{i=1}^{N} X_i \), and refer to its elements as strategy profiles; to be more specific, a strategy profile x is a vector that consists of one strategy per private sector player \(P_i \), say \(x^{i}:=\left( {x_1^i,\ldots , x_K^i } \right) \), that is, \(x:=\left( {x^{1},\ldots ,x^{N}} \right) \). Thus, the main task of the public sector representative consists of ranking individual strategies in each strategy profile based on the public sector preferences; let \(r\left( x \right) :=\left( {r\left( {x^{1}} \right) ,\ldots ,r\left( {x^{N}} \right) } \right) \) denotes such ranking, where \(r\left( {x^{i}} \right) \) is a number between 1 and N that reflects the relative rank of proposal \(x^{i}\) with respect to the other proposals. Without loss of generality, we shall assume that the lower the value assigned to \(r\left( {x^{i}} \right) \), the higher the ranking of \(x^{i}\). In this paper, we distinguish between two types of outcomes, namely strategy profile-induced outcomes and the final outcome of the game. A formal definition of a strategy profile-induced outcome is as follows: a strategy profile \(x \quad \left( {x\in X} \right) \) induced outcome, say \(\alpha \left( x \right) \), of the ordinal game consists of the strategy profile x itself, the induced ranking \(r\left( x \right) \) of the private sector proposals by the public sector representative, and the best induced potential agreement \(f_n \left( x \right) \) between the private sector player who made the best proposal, say \(P_n \), and the public sector representative, that is, \(f_n \left( x \right) :=P_n \); formally, \(\alpha \left( x \right) :=\left( {x,r \left( x \right) ,f_n \left( x \right) } \right) \). The set of all possible strategy profile-induced outcomes shall be denoted by \(A\left( X \right) :=\left\{ {a\left( x \right) ;x\in X} \right\} \). All strategy profiles are of interest to private sector players from an analysis perspective; however, the public sector representative main interest is in only one of these profiles, namely the one that consists of the actual proposals submitted by the private sector players, which we refer to as the final outcome of the game, or equivalently the induced ranking of such profile.

Our ordinal game analysis framework requires the specification of a system of preferences for both the public sector representative and the private sector players.Footnote 2 Hereafter, we shall provide such preference systems for these categories of players.

2.1 Public Sector Player Preference System

2.1.1 Public Sector Player Rationality Assumption

The public sector representative has preferences with respect to proposals, which are expressed in the form of an ordinal ranking \(r\left( x \right) \) and are assumed to be complete and transitive.

This assumption is formalized as follows where, as we stated earlier, the better a proposal, the lower the assigned number to its ranking:

  • \(r\left( {x^{i}} \right) \le r\left( {x^{j}} \right) \) means that the public sector representative weakly prefers proposal \(x^{i}\) over proposal \(x^{j}\).

  • \(r\left( {x^{i}} \right) <r\left( {x^{j}} \right) \) means that the public sector representative strictly prefers proposal \(x^{i}\) over proposal \(x^{j}\).

  • \(r\left( {x^{i}} \right) :=r\left( {x^{j}} \right) \) means that the public sector representative is indifferent between proposal \(x^{i}\) and proposal \(x^{j}\).

  • Completeness: \(r\left( {x^{i}} \right) \le r\left( {x^{j}} \right) \) or \(r\left( {x^{i}} \right) \ge r\left( {x^{j}} \right) \) for all pairs \(\left( {x^{i},x^{j}} \right) \in X_i \times X_j \).

  • Transitivity: If \(r\left( {x^{i}} \right) \le r\left( {x^{j}} \right) \) and \(r\left( {x^{j}} \right) \le r\left( {x^{h}} \right) \), then \(r\left( {x^{i}} \right) \le r\left( {x^{h}} \right) \) for all \(\left( {x^{i},x^{j},x^{h}} \right) \in X_i \times X_j \times X_h \).

2.2 Private Sector Players Preference System

2.2.1 Private Sector Players Rationality Assumption

Each private sector player \(P_i \) has preferences with respect to strategy profile-induced outcomes, which are expressed in the form of an ordinal ranking \(r^{i}\left( {\alpha \left( x \right) } \right) \) over the set of all possible strategy profile-induced outcomes \(A\left( \hbox {X} \right) \) and are assumed to be complete and transitive.

This assumption is formalized by means of ordinal ranking \(r^{i}\) that will be used to rank order the strategy profile-induced outcomes taking account of the preferences of the private sector player \(P_i \left( {i:=1,\ldots ,N} \right) \). In sum, \(r^{i}\) is defined as follows, where the better a strategy profile-induced outcome, the lower the assigned number to its ranking:

  • \(r^{i}\left( {\alpha \left( x \right) } \right) \le r^{i}\left( {\alpha \left( y \right) } \right) \) means that the private sector player \(P_i \) weakly prefers strategy profile-induced outcome \(\alpha \left( x \right) \) over strategy profile-induced outcome \(\alpha \left( y \right) \).

  • \(r^{i}\left( {\alpha \left( x \right) } \right) <r^{i}\left( {\alpha \left( y \right) } \right) \) means that the private sector player \(P_i \) strictly prefers strategy profile-induced outcome \(\alpha \left( x \right) \) over strategy profile-induced outcome \(\alpha \left( y \right) \).

  • \(r^{i}\left( {\alpha \left( x \right) } \right) :=r^{i}\left( {\alpha \left( y \right) } \right) \) means that the private sector player \(P_i \) is indifferent between strategy profile-induced outcome \(\alpha \left( x \right) \) and strategy profile-induced outcome \(\alpha \left( y \right) \).

  • Completeness: \(r^{i}\left( {\alpha \left( x \right) } \right) \le r^{i}\left( {\alpha \left( y \right) } \right) \) or \(r^{i}\left( {\alpha \left( x \right) } \right) \ge r^{i}\left( {\alpha \left( y \right) } \right) \) for all pairs \(\left( {\alpha \left( x \right) ,\alpha \left( y \right) } \right) \in A\left( \hbox {X} \right) \times A\left( \hbox {X} \right) \).

  • Transitivity: If \(r^{i}\left( {\alpha \left( x \right) } \right) \le r^{i}\left( {\alpha \left( y \right) } \right) \) and \(r^{i}\left( {\alpha \left( y \right) } \right) \le r^{i}\left( {\alpha \left( z \right) } \right) \), then \(r^{i}\left( {\alpha \left( x \right) } \right) \le r^{i}\left( {\alpha \left( z \right) } \right) \) for all \(\left( {\alpha \left( x \right) ,\alpha \left( y \right) ,\alpha \left( z \right) } \right) \in A\left( \hbox {X} \right) \times A\left( \hbox {X} \right) \times A\left( \hbox {X} \right) \).

Before we proceed to the main analysis, we provide some important definitions regarding the methodology and the solution concept. Given the notation we provided earlier, we have the following definitions:

Definition 2.1

Ordinal Game of Private Sector Players’ Selection.

Given N private sector players, say \(P_1 , \ldots , P_N \), the corresponding sets of potential proposals considered for analysis purposes \(X_i \) (\(i:=1,\ldots ,N)\), the induced set of strategy profiles \(X:=\prod _{i=1}^N X_i \), the set of strategy profile-induced outcomes \(A\left( \hbox {X} \right) \), and the preference systems used by the public sector representative, say r, and the private sector players, say \(\left\{ {r^{i},i:=1,\ldots ,N} \right\} \), an ordinal game of private sector players’ selection is defined by \(G:=\left( {P,\left( {X_i } \right) _{i\in P} ,A\left( \hbox {X} \right) ,r, \left( {r^{i}} \right) _{i\in P} } \right) \), where \(P:=\left\{ {P_1 , \ldots , P_N } \right\} \).

Definition 2.2

Best Response Correspondence.

Let \(x^{-i}\) denotes the strategy profile x without the proposal \(x^{i}\) of the \(i^{th}\) private sector player, that is, \(x^{-i}\in \prod _{j=1,j\ne i}^N X_j \). Then, a strategy profile x could be rewritten as \(x:=\left( {x^{i},x^{-i}} \right) \). For private sector player \(P_i \), his best response correspondence with respect to a specific strategy profile \(x^{-i}\) played by the other private sector players, say \(x^{i^{*}}\left( {x^{-i}} \right) \), refers to the subset of his strategies that qualify as a best response to \(x^{-i}\); that is,

$$\begin{aligned} x^{i^{*}}\left( {x^{-i}} \right) :=\left\{ {x^{i}\in X_i \left| {r^{i}\left( {\alpha \left( {x^{i},x^{-i}} \right) } \right) \le r^{i}\left( {\alpha \left( {z^{i},x^{-i}} \right) } \right) ,\forall z^{i}\in X_i } \right. } \right\} . \end{aligned}$$

Definition 2.3

Ordinal Non-cooperative Equilibrium (ONE).

A strategy profile \(\hat{x} :=\left( {\hat{x}^{i},\hat{x}^{-i}} \right) \) is an ordinal non-cooperative equilibrium (ONE) of the private sector players’ selection game G if and only if \(\hat{x}^{i}:=x^{i^{*}}\left( {\hat{x}^{-i}} \right) \) for all \(i\in \left\{ {1,\ldots ,N} \right\} \) and players are assumed to make decisions independently. In sum, a ONE is a strategy profile that no player is likely to unilaterally deviate from. Note that a non-cooperative ordinal game G may have multiple ONEs, a single ONE or no ONE.

2.3 Contract Award

Assuming that the ordinal game has a non-cooperative equilibrium, say \(\hat{x}\), the final outcome of the game is the \({\hat{x}} \)-induced ranking of the proposals submitted by the private sector players to the public sector representative. In sum, a contract shall be awarded to the private sector player, say \(P_n \), who submitted the proposal with the highest rankings; that is, \(r\left( {{\hat{x}} ^{n}} \right) :=1\).

Hereafter, we shall describe an algorithm that we propose for finding an ordinal non-cooperative equilibrium (ONE) of an ordinal game, if any exists.

2.4 General Framework for PPPs: A Solution Algorithm

Inputs: Two main inputs are required to operationalize this framework. The first input is a set of strategy profiles X to be used for analysis; that is, for each private sector player \(P_i \quad \left( {i:=1,\ldots ,N} \right) \), a set of potential proposals \(X_i \) is available. The second input is a description of the preference systems of the players participating in the game.

  • Step 1. Ranking of proposals from a public sector perspective For each strategy profile \(x\in X\), rank its proposals \(x^{i}s\) according to the public sector representative preferences, thus producing a ranking \(r\left( x \right) :=\left( {r\left( {x^{1}} \right) ,\ldots ,r\left( {x^{N}} \right) } \right) \) for each x. Then sort \(r\left( {x^{1}} \right) ,\ldots ,r\left( {x^{N}} \right) \) in ascending order and set \(f_n \left( x \right) \) to the proposal on the top of the list. In sum, determine the set of strategy profile-induced outcomes \(A\left( X \right) :=\left\{ {a\left( x \right) ;x\in X} \right\} \), where \(\alpha \left( x \right) :=\left( {x,r\left( x \right) ,f_n \left( x \right) } \right) \). In practice, the ranking of proposals could be done by a simple lexicographic ordering system, an MCDM method (e.g. ELECTRE methods, PROMETHEE methods, AHP, TOPSIS) or a mathematical programming-based methodology (e.g. DEA).

  • Step 2. Ranking of strategy profile-induced outcomes from a private sector perspective For each private sector player \(P_i \left( {i:=1,\ldots ,N} \right) \), rank order the strategy profile-induced outcomes, \(\alpha \left( x \right) :=\left( {x,r \left( x \right) ,f_n \left( x \right) } \right) \), computed at the previous step according to \(P_i \) preferences. To be more specific, for each private sector player \(P_i \), strategy profile-induced outcomes, \(\alpha \left( x \right) :=( x^{1},\ldots ,x^{i},\ldots ,x^{N},r\left( {x^{1}} \right) ,\ldots ,r\left( {x^{i}} \right) \), \(\ldots ,r\left( {x^{N}} \right) ,f_n \left( x \right) )\); \(x\in X\), are first sorted in ascending order with respect to the ranks assigned by the public sector representative, \(r\left( {x^{i}} \right) \). Notice that, for each private sector player \(P_i \), the set of strategy profile-induced outcomes would consist of two categories. The first category or subset, say \(X_1^i \), consists of those strategy profile-induced outcomes where player \(P_i \) is top-ranked by the public sector representative; that is, \(X_1^i :=\left\{ {x\in X\left| {r\left( {x^{i}} \right) :=1} \right. } \right\} \), whereas the second category or subset, say \(X_2^i \), consists of those strategy profile-induced outcomes where player \(P_i \) is outranked; that is, \(X_2^i :=\left\{ {x\in X\left| {r\left( {x^{i}} \right) \ne 1} \right. } \right\} \). Then, these sorted subsets of strategy profile-induced outcomes \(X_1^i \) and \(X_2^i \) are each lexicographically ordered according to \(x^{i}\) entries and \(P_i \) preferences if and only if \(X_1^i \) is non-empty—otherwise none of the proposals of player \(P_i \) are competitive enough to qualify \(P_i \). Finally, ranks by \(P_i \) are assigned accordingly. Notice that the above-mentioned condition enhances the computational efficiency of our algorithm, on the one hand, and allows one to discard any private sector player whose proposals are outranked by other private sector players’ proposals, on the other hand. In order to keep track of the public sector rankings, for each strategy profile-induced outcome \(\alpha \left( x \right) \), we consider a corresponding vector of private sector rankings; that is,

    $$\begin{aligned} r'\left( x \right) : = \left( {{r^1}\left( x \right) , \ldots ,{r^i}\left( x \right) ,\ldots ,{r^N}\left( x \right) } \right) , \end{aligned}$$

    where \(r^{i}\left( {x^{i}} \right) \) denotes the rank assigned by \(P_i \) to strategy profile-induced outcome \(\alpha \left( x \right) \). Note also that one could use a simple lexicographic ordering system, an MCDM method (e.g. ELECTRE methods, PROMETHEE methods, AHP, TOPSIS) or a mathematical programming-based methodology (e.g. DEA) to obtain these rankings.

  • Step 3. Identification of ordinal non-cooperative equilibria In this step, one ordinal non-cooperative equilibrium (ONE) or many (ONEs) shall be identified, if any exists. Notice that the ordered strategy profile-induced outcomes produced in the previous step along with the corresponding vectors of private sector players rankings; that is,

    $$\begin{aligned}&\left( {\alpha \left( x \right) ;r^{\prime }\left( x \right) } \right) \\&\quad :=\left( {x^{1},\ldots ,x^{N};r\left( {x^{1}} \right) ,\ldots ,r\left( {x^{N}} \right) ,f_n \left( x \right) ;r^{1}\left( x \right) ,\ldots ,r^{N}\left( x \right) } \right) ;\quad x\in X, \end{aligned}$$

    are, by construction, already sorted in such a way that the one(s) on the top of this list have the vector of private sector rankings, \(r^{{\prime }}\left( x \right) :=\left( {r^{1}\left( x \right) ,\ldots ,r^{N}\left( x \right) } \right) \), with the smallest entries. Therefore, if a ONE exists, all the entries of \(r^{\prime }\left( x \right) \) corresponding to the top-ranked \(\alpha \left( x \right) \) or \(\alpha \left( x \right) \)s should be equal to one; otherwise, a generalized Nash equilibrium of order \(\left( {r^{1}\left( x \right) ,\ldots ,r^{N}\left( x \right) } \right) \) would be the best outcome of the game.

Output: One ordinal non-cooperative equilibrium (ONE) or several (ONEs), if any exists.

As stated in the following theorem, our algorithm converges in a finite number of steps to a Generalized Nash Equilibrium.

Theorem 2.1

Given a static non-cooperative ordinal game of complete information involving one public sector player and several private sector players, the proposed ordinal game theory algorithm identifies, in a finite number of iterations, an ordinal non-cooperative equilibrium (ONE) or several (ONEs), if any exists, or a Generalized Nash Equilibrium of a given order.

Proof

In fact, the proposed algorithm could be viewed as a construction method that builds a solution by following a finite sequence of steps, each involving a ranking task that takes account of the preference system or perspective of a player - obviously each ranking task requires a finite number of iterations, as the number of proposals is finite. The final outcome is an ordered list of strategy profile-induced outcomes along with the corresponding vectors of private sector players rankings; that is,

$$\begin{aligned} (\alpha (x);r^{\prime }(x));-(x^1,\cdots ,x^{N};r(x^1),\cdots ,r(x^{N}),f_{n}(x);r^1(x),\cdots ,r^{N}(x));x\in X, \end{aligned}$$

where each\((\alpha (x);r^{\prime }(x))\) takes account of all players? perspectives. Therefore, by design, the proposed algorithm converges in a finite number of iterations and its order of complexity depends on the choice of the ranking algorithm. The nature of the outcome, however, is data-driven and could be one Generalized Nash Equilibrium of order \((1,\ldots ,1)\); that is a ONE, several Generalized Nash Equilibria of order \((1,\ldots ,1)\); that is, several ONEs, or a Generalized Nash Equilibrium of an order\(r^{\prime }(x)\).

Recall that, as compared to the ordinal game theory frameworks proposed by Cruz and Simaan [25] and Xu [26], our framework is more general in that it can model games with any finite number of players, whereas [25] model only considers two players and [26] model considers the cases of two and three players, respectively.

The performance evaluation of PPP projects at different stages of their life cycle requires the specification of performance criteria and their measures—often referred to as key performance indicators (KPIs). Given the nature of PPP projects, performance criteria are divided into two broad categories depending on the perspective from which one looks at the performance evaluation exercise, namely public sector perspective and private sector perspective. One could further refine this classification by dividing performance criteria into several categories depending on a more detailed classification of stakeholders (e.g. national, regional and/or local governments, governmental agencies, state-owned entities, private sub-contractors, private investors, financiers, insurers). One might argue that performance criteria and measures are chosen by the public sector, and therefore, the public sector perspective should prevail; however, for the public sector to generate interest into the PPP project from the private sector, the private sector perspectives should be taken account of. In this paper, we are focusing on the performance criteria and measures most relevant to the operationalization of the proposed ordinal game theory framework for the selection of private sector partners; therefore, only those criteria most relevant to the tendering-related phases and stages of PPP projects are considered—see “Appendix 1” for the typical PPP project phases and stages relevant to the pre-tendering and the tendering process [28–30]. Notice that, at the different phases of the process, different sets of criteria are required. In “Appendix 2” we provide the reader with a general classification of performance criteria commonly used in assessing PPP projects at the tendering phase divided into two categories depending on whether they are used for assessing bidders or proposals—see [31, 32] for more details.

The design and evaluation of proposals involve proactive planning, which in turn involves forecasting PPP project requirements in terms of resources as well as time schedules. Such forecasting task is typically made based on limited information, on the one hand, and under a set of assumptions linking the past, the present and the future, on the other hand. Given the uncertainty that governs our business environments and the nature of forecasts that drive planning, the process of implementing a PPP project along with its intermediate and final outcomes is generally worse or better than originally expected—these highly likely deviations from the expected targets are commonly referred to as downside and upside risks, respectively. In practice, the question both public and private sectors’ players are concerned with is not whether to take risks, but what are the “reasonable” levels of risks to take? Obviously, the answer to this question depends on the risk appetite of the players (e.g. risk neutral, risk seeking or risk averse); however, to reach a decision one needs to start by identifying and recognizing risks, measuring and assessing them, and choosing or designing the tools for managing them. Risk is an abstract concept which proves to be often difficult to define and measure with any precision. In this paper, we adopt the following definition. The risk associated with a PPP project is multidimensional in nature. We define the risk associated with a specific dimension (e.g. activity, process, player, environment) as the deviation of its actual outcome (e.g. timing, cost, price, quality, behaviour) from its expected one. We shall refer to such deviation as the event associated with the dimension. The risk exposure associated with an event is typically measured by the product of the probability of the event taking place and the magnitude of the resulting loss or gain. However, in practice, one would have to refine such measure by taking account of the extent to which the event will have an impact on the overall project. For example, one could classify the risk associated with an event into one of the following categories: high probability–high impact, low probability–high impact, high probability–low impact, and low probability–low impact. Then act upon the risk accordingly. Hereafter, and as part of providing the necessary tools to operationalize our proposed framework, we provide a classification of typical risk categories or packages facing PPP projects along with a checklist of risk factors within each package—see “Appendix 3”. For additional references on risk packages, the reader is referred to [33–41]. The information in “Appendix 3” is provided for guidance only, but does not replace the risk identification stage where one has to identify the relevant risks associated with a PPP project. Risk identification approaches and related methods fall into three main categories: (1) the intuitive approach, which is often operationalized by brainstorming to generate ideas by one or several groups and could make use of interviews and self-assessment techniques, nominal group techniques, and Delphi techniques, (2) the inductive approach is concerned with “what if” type of analyses, which is often operationalized using a combination of methodologies and tools such as generic and project-specific checklists, interviews and surveys, nominal group techniques, Delphi techniques, risk registers, SWOT analysis, hazard and failure analyses such as failure modes and effects criticality analysis (FMECA) and its variants like hazard and operability studies (HAZOPS), impact analysis, Structured What If Technique (SWIFT), Business, Political, Economic, Social and Technological (BPEST) analysis, Political, Economic, Social, Technical, Legal and Environmental (PESTLE) analysis, and (3) the deductive approach is concerned with “so how” type of analyses, which is often operationalized using a combination of methodologies and tools such as hindsight and hazard and failure analyses like fault tree analysis (FTA) and event tree analysis (ETA) and risk registers. For more information, the reader is referred to [42, 43].

Once the relevant risk packages and the corresponding risk factors associated with a PPP project are chosen by the relevant stakeholder(s), one would have to evaluate them. In this paper, we refer to risk evaluation or assessment as the process of measuring risk whether on a quantitative scale or a qualitative scale. A common aim of this exercise is to determine the likely financial impact of all the risks considered relevant to the PPP project under evaluation. Risk evaluation methodologies could be classified into three main categories, namely qualitative methodologies, quantitative methodologies and hybrid methodologies. Qualitative methodologies are typically concerned with describing the likely consequences of the risks identified and considered relevant to the PPP project under evaluation, without much effort to quantify their probability of occurrence, although a ranking of such risks that reflects “priority” is often devised. Examples of qualitative methodologies that are commonly used or have the potential to be used include information systems methods and tools to collect, organize, store and analyse risk-related information (e.g. databases such as risk registers, also known as risk matrices or risk logs; probability-impact tables, scenario analysis, survey questionnaires, Fuzzy metrics), classification and clustering methods and tools to classify or categorize risks based, for example, on their probability of occurrence, and cost and schedule impact (e.g. Delphi techniques, but quantitative methods could also be used such as consensus clustering methods, constrained clustering methods, neural networks), ranking methods to prioritize risks (e.g. Delphi techniques, but quantitative methods could also be used such as multi-criteria decision analysis ranking methods), benchmarking analysis such as value-for-money (VfM) analysis and data envelopment analysis and other methods (e.g. analysis of inter-connected decision areas (AIDA), conflict analysis, robustness analysis, strategic options development and analysis (SODA), soft systems methodology (SSM) and the strategic choice method, value chain analysis). Quantitative methodologies, on the other hand, are concerned with determining the likelihood of the relevant risks and their impacts especially in terms of money and/or time. This category of quantitative methodologies could be further divided into two sub-categories, namely deterministic methods and probabilistic methods. Sensitivity analyses (e.g. one-factor-at-the-time analysis, multiple-factors-at-the-time analysis, scenario analysis such as pessimistic, realistic and optimistic scenarios) are the most commonly used deterministic methods. Examples of probabilistic methods include decision analysis methods and tools (e.g. decision trees, mean-end analysis, influence diagrams, objective and subjective conditional probability models, Bayesian theory and probability distributions, stochastic dominance), reliability analysis—also known as survival analysis—including estimation of system reliability methods such as first-order reliability methods and simulation methods (e.g. Monte Carlo simulation, Latin hyper-cube sampling). As to hybrid methodologies, as the name suggests, they make use of a mixture of qualitative and quantitative methods. For more details, the reader is referred to [33–35, 39, 45–51].

Once a PPP project-related risks have been identified and assessed, the next critical step is concerned with risk allocation; to be more specific, at this stage one would have to decide on which risks to allocate to the public sector players, which risks to allocate to the private sector players, and which risks to share by both parties. In practice, risk allocation is a sequential decision-making process with feedback adjustment mechanisms, which requires proper costing of risks and negotiation of risk premiums; in general, however, whoever is in a better position to handle a specific risk, is responsible for its management—the reader is referred to [38] for a detailed presentation of a typical risk allocation process in PPPs along with a three-level classification of risks that is relevant to risk allocation, namely macro-level risks, meso-level risks and micro-level risks. As risks are shaped by the perspectives from which we look at them, some studies have investigated this aspect such as [40, 41, 52, 53]. Quantitative analysis and tools to assist with decision-making in risk allocation include game theory as a modelling and analysis framework—see, for example [17].

Once a partner or consortium of partners has been awarded a PPP contract, the public sector—eventually in cooperation with the private sector partner(s)—would have to prepare the environment for the implementation of the PPP project. Such environment preparation for a successful implementation requires one to take account of the critical success factors (CSFs) by putting in place the related ingredients or mechanisms to enhance the likelihood of a successful PPP. Note, however, that some CSFs are more or less controllable than others; therefore, in this paper we propose our own classification of CSFs where the classification criterion is the nature of the PPP environment, that is, internal environment versus external environment-related CSFs—see “Appendix 4” for such classification along with a typical list of CSFs relevant to each environment.

In the next section, we provide a PPP scenario to illustrate the workings of our proposed framework.

3 Analysis of Scenarios

In this section, we illustrate the proposed methodology by means of a realistic, but small scale, scenario. Such scenario could be described as follows. The PPP project is concerned with a transportation infrastructure (e.g. tram network). It involves a single public sector player who represents several parties (e.g. city council and regional government) and two private sector players (e.g. supplier of vehicles or trams, consortium supplier of the design and construction of the network). The project is operated by the public sector represented by the city council. In addition, a couple of project-related services are required, namely a network construction project manager supplied, for example, by the private sector represented by a consulting firm, and tram vehicle testing supplied, for example, by the public sector represented by the city council. It is assumed that the private sector players agree to a fixed-price contract and to bear some of the project risks in exchange of an agreed upon financial compensation (e.g. savings for the public sector). The bidding process for the PPP project requires the private sector players to submit proposals to the public sector representative, where each proposal consists of three contract terms, namely price, delivery time and risk. To be more specific, price refers to the amount of money that a private sector player is willing to receive for undertaking the project, whereas delivery time refers to the expected time period (expressed in years) required to deliver or complete the project and its ownership transferred to the public sector representative who will be operating the project, and risk refers to the percentage of (e.g. operational, financial, technical) risk, say \(\rho \), which the private sector player is willing to bear with the remaining percentage \(\left( {1-\rho } \right) \) allocated to the public sector.

In the remainder of this section, we shall focus on bids for the tram network construction. A similar exercise could be performed for the bids on the supply of vehicles or trams. Conceptually, the PPP project is modelled as an ordinal game involving a single public sector player and a couple of private sector players. These private sector players compete for contracting with the public sector player through the features of their proposals, which will be ranked by the public sector representative who will grant the contract to the highest ranked player; in sum, the outcome of the game is a ranking by the public sector representative of the private sector players’ proposals. As far as the real-life case that inspired this research is concerned, it is also assumed that in case of tie (i.e. both private sector players submit identical proposals), the public service representative shall make use of additional information to break the tie such as private sector players experiences and their track records on completing these types of project successfully. Hereafter, we summarize the main assumptions underlying the public sector player preference system and the private sector players’ preference systems.

3.1 Public Sector Player Preference System

The public sector representative preferences with respect to the three contract terms, namely price, delivery time and risk, could be summarized as follows. More importance is given to price, then to risk and then to delivery time. In sum, the public sector representative ranks proposals according to their price first. Proposals with the same price are then ranked according to risk. Finally, proposals with the same price and risk are ranked according to delivery time. In other words, the preference system of the public sector player is a lexicographic ordering system with price being the first criterion, risk being the second criterion, and delivery time being the third and last criterion. Note that lexicographic ordering systems are complete and transitive. Therefore, the public sector player rationality assumption is satisfied—see Sect. 2. In addition, from a public sector perspective, proposals with lower prices are preferred to proposals with higher prices; proposals with higher risk proportion assumed by a private sector player are preferred to those proposals with lower risk proportions; and proposals with shorter delivery times are preferred to proposals with longer delivery times. Last, but not least, it is assumed that, in the case of tie (i.e. both private sector players submit identical proposals), the public service representative shall make use of additional information to break the tie such as private sector players experiences and their track records on completing this type of projects successfully. In the scenario under consideration, it is assumed that private sector player, say \(P_1 \), has a better profile with respect to previous experience and its track record on completing this type of infrastructure project successfully.

3.2 Private Sector Players’ Preference Systems

The private sector players have the following preferences with respect to price, delivery time and risk sharing. Obviously, both private sector players would strictly prefer to win the PPP contract and, therefore, would design competitive proposals; in sum, they would adopt a rational behaviour.

In sum, private sector player \(P_1 \) is assumed to have a lexicographic ordering of his preferences with price being the first criterion, and proposals are ranked with respect to this criterion in descending order of price, delivery time being the second criterion, and proposals are ranked with respect to this criterion in ascending order of delivery time, and risk being the third and last criterion, and proposals are ranked with respect to this criterion in ascending order of the private sector risk sharing proportion. Therefore, \(P_1 \) prefers proposals with higher prices to proposals with lower prices—this preference could be motivated by the player’s confidence that its reputation and previous achievements would balance the higher price bid; he prefers proposals with shorter delivery times to proposals with longer delivery times—this preference could be motivated by the desire to minimize the impact of any unfavourable changes in the economy over the delivery period, and he prefers proposals with lower risk sharing proportions to proposals with higher risk sharing proportions—this preference has obvious motivations including the control of potential additional expenses. Finally, it is assumed that private sector player \(P_1 \) has come up with three price options, namely \(\left\{ {\pounds 510\; \text {million},\pounds 560\; \text {million},\pounds 630\; \text {million}} \right\} \), two risk sharing schema, namely \(\left\{ {55, 60\,\% } \right\} \), and two delivery times options, namely \(\left\{ {3 \;\text {years}, 4\; \text {years}} \right\} \). Thus, \(P_1 \) has the following set of strategies:

$$\begin{aligned} \left\{ {{\begin{array}{l} {\left( {510{,}55\,\%, 3} \right) ,\left( {510{,}60\,\%, 3} \right) ,\left( {510{,}55\,\%, 4} \right) ,\left( {510{,}60\,\%, 4} \right) , } \\ {\left( {560{,}55\,\%, 3} \right) ,\left( {560{,}60\,\%, 3} \right) ,\left( {560{,}55\,\%, 4} \right) ,\left( {560{,}60\,\%, 4} \right) ,}\\ {\left( {630{,}55\,\%, 3} \right) ,\left( {630{,}60\,\%, 3} \right) ,\left( {630{,}55\,\%, 4} \right) ,\left( {630,60\,\%, 4} \right) } \\ \end{array} }} \right\} . \end{aligned}$$

On the other hand, private sector player \(P_2 \) is assumed to have a lexicographic ordering of his preferences with risk being the first criterion, and proposals are ranked with respect to this criterion in descending order of the private sector risk sharing proportion, delivery time being the second criterion, and proposals are ranked with respect to this criterion in descending order of delivery time, and price being the third and last criterion, and proposals are ranked with respect to this criterion in ascending order of price. Therefore, \(P_2 \) prefers proposals with higher risk sharing proportions to proposals with lower risk sharing proportions—this preference could be motivated by the confidence of the player in its ability to manage risk in an effective manner; he prefers proposals with longer delivery times to proposals with shorter delivery times—this preference could be motivated, for example, by previous commitments of resources and suppliers’ projections of their own delivery times; and he prefers proposals with lower prices to proposals with higher prices; that is, he prefers to bid lower to secure the contract. Finally, it is also assumed that private sector player \(P_2 \) has come up with three price options, namely \(\left\{ {\pounds 480\,\text {million},\pounds 560\,\text {million},\pounds 610\,\text {million}} \right\} \), two risk sharing schema, namely \(\left\{ {55, 65\,\% } \right\} \), and two delivery times options, namely \(\left\{ {4\,\text {years},6\,\text {years}} \right\} \). Thus, \(P_2 \) has the following set of strategies:

$$\begin{aligned} \left\{ {{\begin{array}{l} {\left( {480{,}55\,\%, 4} \right) ,\left( {480{,}65\,\%, 4} \right) ,\left( {480{,}55\,\%, 6} \right) ,\left( {480{,}65\,\%, 6} \right) ,}\\ {\left( {560{,}55\,\%, 4} \right) ,\left( {560{,}65\,\%, 4} \right) ,\left( {560{,}55\,\%, 6} \right) ,\left( {560{,}65\,\%, 6} \right) ,} \\ {\left( {610{,}55\,\%, 4} \right) ,\left( {610{,}65\,\%, 4} \right) , \left( {610{,}55\,\%, 6} \right) ,\left( {610{,}65\,\%, 6} \right) } \\ \end{array} }} \right\} . \end{aligned}$$

Recall that lexicographic ordering systems are complete and transitive. Therefore, the private sector players’ rationality assumption is satisfied—see Sect. 2.

Table 1 Ranking of proposals according to the public sector preference system
Full size table
Table 2 Summary of the rankings of strategy profile-induced outcomes according to the private sector player \(P_1 \) preference system
Full size table
Table 3 Summary of the rankings of strategy profile-induced outcomes according to the private sector player \(P_2 \) preference system
Full size table
Table 4 Summary of the rankings of strategy profile-induced outcomes according to the private sector players \(P_1 \) and \(P_2 \) preference systems
Full size table

We next apply our proposed methodology to the above ordinal game, which is summarized in the following steps.

  • Step 1. Ranking of proposals from a public sector perspective Based on the public sector player preference system and the tie breaking rule outlined above, a ranking of the private sector players’ proposals is obtained—see Table 1. For example, strategy profile, [(510,55 %, 3); (480,55 %, 4)], where \(P_1 \) proposal is (510,55 %, 3) and \(P_2 \) proposal is (480,55 %, 4), is ranked by the public sector player according to his or her preferences resulting in \(P_2 \) being ranked first and then \(P_1 \) is ranked second, because the public sector player prefers proposals with lower prices to those with higher prices, and price matters more than delivery time and risk—this outcome is represented in the table by ranking:

    $$\begin{aligned} r\left( {\left( {510{,}55\,\%, 3} \right) ; \left( {480{,}55\,\%}, 4 \right) } \right) :=\left( {2, 1} \right) . \end{aligned}$$

    The rest of the table is obtained in a similar way. Notice that cell (7,5) corresponds to a strategy profile where there is a tie between the proposals of \(P_1 \) and \(P_2 \), which is broken by making use of the fact that \(P_1 \) has a better profile than \(P_2 \) with respect to its previous experience and its track record on completing this type of infrastructure project successfully.

  • Step 2. Ranking of proposals from a private sector perspective The strategy profile-induced outcomes computed at the previous step are now ranked based on each private sector player preference system—see Tables 2 and 3 for ranks, which are then summarized in Table 4, where different colours are used to highlight the rankings resulting from different preference systems of players. Notice that \(P_1 \) (respectively, \(P_2 )\) would assign a higher ranking to those strategy profile-induced outcomes that privilege him or her, namely those entries in Table 1 with \(r\left( x \right) :=\left( {1,2} \right) \) (respectively, \(r\left( x \right) :=\left( {2,1} \right) )\). However, from a computational perspective, the ranking operation is more efficient by sorting the entries of Table 1 column by column for \(P_1 \) and row by row for \(P_2 \). To be more specific, each column (respectively, row) of Table 1 is first sorted in a lexicographic order where the first (respectively, second) entry of the vector of ranks assigned by the public sector player is sorted in ascending order. The sorted columns (respectively, rows) are then sorted again as many times as there are contract terms based on the preference system of \(P_1 \) (respectively, \(P_2 )\) in a sequential manner.

For illustration purposes, consider the fifth column of Table 1 along with the corresponding proposals from \(P_1 \) and \(P_2 \) (i.e. strategy profiles), the induced rankings (i.e. rankings by the public sector player \(P_0 \) of the strategy profiles) and the induced potential agreements (i.e. the private sector players who made the best proposal within each strategy profile)—see Table 5. Note that, when more than two private sector players are considered, the strategy profiles \(x:=\left( {x^{1},x^{2}} \right) \) are replaced by \(x:=\left( {x^{1},\ldots ,x^{N}} \right) \) where N denotes the number of private sector players. Note also that, when more than three contractual terms are considered, each \(x^{i}\) would be a vector of dimension K where K denotes the number of contractual terms specified by the public sector.

Table 5 List of strategy profiles including all proposals of \(P_1 \) and a single proposal of \(P_2 \) and the corresponding induced rankings and induced potential agreements
Full size table

In this case, this list is already sorted in descending order of the first entry of the vector of ranks by the public sector. This sorted list would then have to be sorted again in a lexicographic order based on prices first to reflect the preferences of \(P_1 \) (i.e. higher prices are preferred to lower ones), where the sorting is done within each of the sub-lists where \(P_1 \) is ranked first (respectively, second) separately, namely \(X_1^1 \) and \(X_2^1 \)— see Table 6.

Table 6 List of strategy profiles sorted according to the preference of \(P_1 \) on price
Full size table

This sorted list would then again have to be sorted in ascending order of delivery times and then in ascending order of risk sharing proportion, which is already done and leads to the ranking by \(P_1 \) of the column entries as shown in Table 7 and Table 2.

Table 7 List of strategy profile-induced outcomes sorted and ranked according to \(P_1 \) preferences
Full size table

Applying the above described logic to each column of Table 1 at a time leads to Table 2. Also, applying the above described logic to each row of Table 1 at a time leads to Table 3. Finally, Tables 2 and 3 are summarized into Table 4 for presentation purposes.

  • Step 3. Identification of ordinal non-cooperative equilibria Given the rankings of strategy profile-induced outcomes by the private sector players \(P_1 \) and \(P_2 \)—see Table 4—the strategy profile-induced outcome \((\left( {630,55\,\%, 3} \right) ;\left( {480,65\,\%, 6} \right) ;\left( {1,1} \right) )\) is the unique optimal non-cooperative equilibrium (ONE) of the game.

Output: Optimal generalized Nash equilibrium \((\left( {630,55\,\%, 3} \right) ;\left( {480,65\,\%, 6} \right) ;( {1,1} ))\).

This outcome could be used by both the public sector representative and the private sector players for decision-making. In sum, from the private sector players’ perspective, the optimal generalized Nash equilibrium suggests that player \(P_1 \) would be better off putting forward proposal \(({630,55\,\%, 3})\) and player \(P_2 \) would be better off putting forward proposal \(({480,65\,\%, 6})\). As to the public sector perspective, the optimal generalized Nash equilibrium suggests that the proposal of \(P_2 \) is more attractive than the proposal of \(P_1 \) except for the delivery time. In this simplified situation, common sense suggests that the PPP contract would be awarded to player \(P_2 \); however, in practice, this solution might suggest that further negotiation is necessary to avoid the potential drawbacks of a delivery time twice as much as the one proposed by player \(P_1 \).

4 Conclusions

This paper is concerned with public–private partnership (PPP) projects and the choice of private sector partners. Unlike previous Cardinal game theory-based analyses of PPP projects with respect to a range of decisions, this paper proposes an ordinal game theory-based framework. In addition, we propose tools for its operationalization including a general algorithm for ranking proposals that take account of the different perspectives of all players. To be more specific, the proposed algorithm is designed to find an optimal generalized Nash equilibrium. We illustrated the application of this algorithm on a realistic, yet small scale, scenario. The main features of the proposed algorithm could be summarized as follows. First, it can handle any number of private sector players and any number of contractual terms and related performance criteria. Second, it determines a single ranking of proposals or bidders that take account of multiple performance criteria and reflects both the public sector perspective and the private sector perspective. Third, it can be used by the private sector players to analyse any set of potential proposals most likely to be submitted by bidders and to assist with the design and choice of bidding strategies. Fourth, it can be used by the public sector player to analyse any set of potential proposals most likely to be submitted under any set of contractual terms and to assist with the choice of a realistic set of contractual terms and their performance measures. Last but not least, the proposed algorithm provides a means for automating the analysis process, which would save a valuable amount of time for practitioners. In sum, the proposed ordinal game theory framework is intended to assist both the public sector and the private sector with the analysis of scenarios and to guide decision-making.