Skip to main content
SpringerLink
Log in

Interior-Point Lagrangian Decomposition Method for Separable Convex Optimization

  • Published:
Journal of Optimization Theory and Applications Aims and scope Submit manuscript

Abstract

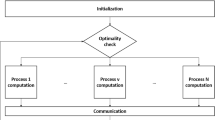
In this paper, we propose a distributed algorithm for solving large-scale separable convex problems using Lagrangian dual decomposition and the interior-point framework. By adding self-concordant barrier terms to the ordinary Lagrangian, we prove under mild assumptions that the corresponding family of augmented dual functions is self-concordant. This makes it possible to efficiently use the Newton method for tracing the central path. We show that the new algorithm is globally convergent and highly parallelizable and thus it is suitable for solving large-scale separable convex problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Xiao, L., Johansson, M., Boyd, S.: Simultaneous routing and resource allocation via dual decomposition. IEEE Trans. Commun. 52(7), 1136–1144 (2004)

    Article  Google Scholar 

  2. Gondzio, J., Sarkissian, R.: Parallel interior point solver for structured linear programs. Math. Program. 96, 561–584 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  3. Venkat, A., Hiskens, I., Rawlings, J., Wright, S.: Distributed MPC strategies with application to power system automatic generation control. IEEE Trans. Control Syst. Technol. 16(6), 1192–1206 (2008)

    Article  Google Scholar 

  4. Necoara, I., Suykens, J.A.K.: Application of a smoothing technique to decomposition in convex optimization. IEEE Trans. Autom. Control 53(11), 2674–2679 (2008)

    Article  MathSciNet  Google Scholar 

  5. Zhao, G.: A Lagrangian dual method with self-concordant barriers for multi-stage stochastic convex programming. Math. Program. 102, 1–24 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  6. Bertsekas, D.P., Tsitsiklis, J.N.: Parallel and Distributed Computation: Numerical Methods. Prentice-Hall, Englewood Cliffs (1989)

    MATH  Google Scholar 

  7. Lemarechal, C., Ouorou, A., Petrou, G.: A bundle-type algorithm for routing in telecommunication data networks. Comput. Optim. Appl. (2008)

  8. Kontogiorgis, S., De Leone, R., Meyer, R.: Alternating direction splittings for block angular parallel optimization. J. Optim. Theory Appl. 90(1), 1–29 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  9. Chen, G., Teboulle, M.: A proximal-based decomposition method for convex minimization problems. Math. Program. 64, 81–101 (1994)

    Article  MathSciNet  Google Scholar 

  10. Kojima, M., Megiddo, N., Mizuno, S., Shindoh, S.: Horizontal and vertical decomposition in interior point methods for linear programs. Dept. of Mathematical and Computing Sciences Technical report, Tokyo Institute of Technology (1993)

  11. Kortanek, K.O., Potra, F., Ye, Y.: On some efficient interior-point methods for nonlinear convex programming. Linear Algebra Appl. 152, 169–189 (1991)

    Article  MATH  MathSciNet  Google Scholar 

  12. Tseng, P.: Global linear convergence of a path-following algorithm for some monotone variational inequality problems. J. Optim. Theory Appl. 75(2), 265–279 (1992)

    Article  MATH  MathSciNet  Google Scholar 

  13. Zhu, J.: A path following algorithm for a class of convex programming problems. Math. Methods Oper. Res. 36(4), 359–377 (1992)

    Article  MATH  Google Scholar 

  14. Hegland, M., Osborne, M.R., Sun, J.: Parallel interior point schemes for solving multistage convex programming. Ann. Oper. Res. 108(1–4), 75–85 (2001)

    Article  MATH  MathSciNet  Google Scholar 

  15. Miele, A., Moseley, P.E., Levy, A.V., Coggins, G.M.: On the method of multipliers for mathematical programming problems. J. Optim. Theory Appl. 10, 1–33 (1972)

    Article  MATH  MathSciNet  Google Scholar 

  16. Nesterov, Y., Nemirovskii, A.: Interior Point Polynomial Algorithms in Convex Programming. SIAM Studies in Applied Mathematics. Society for Industrial and Applied Mathematics, Philadelphia (1994)

    MATH  Google Scholar 

  17. Renegar, J.: A Mathematical View of Interior-Point Methods for Convex Optimization. MPS-SIAM Series on Optimization. Philadelphia (2001)

  18. Mayne, D.Q., Rawlings, J.B., Rao, C.V., Scokaert, P.O.M.: Constrained model predictive control: stability and optimality. Automatica 36(7), 789–814 (2000)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Automatic Control and Systems Engineering Department, University Politehnica Bucharest, 060042, Bucharest, Romania

    I. Necoara

  2. Department of Electrical Engineering (ESAT), Katholieke Universiteit Leuven, 3001, Leuven–Heverlee, Belgium

    I. Necoara & J. A. K. Suykens

Authors
  1. I. Necoara
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. J. A. K. Suykens
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to I. Necoara.

Additional information

Communicated by D.Q. Mayne.

We acknowledge financial support from Flemish Government: FWO Projects G.0226.06, G.0302.07.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Necoara, I., Suykens, J.A.K. Interior-Point Lagrangian Decomposition Method for Separable Convex Optimization. J Optim Theory Appl 143, 567–588 (2009). https://doi.org/10.1007/s10957-009-9566-8

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10957-009-9566-8

Keywords

Search

Navigation