Switching Interacting Particle Systems: Scaling Limits, Uphill Diffusion and Boundary Layer

Abstract

This paper considers three classes of interacting particle systems on ${{\mathbb {Z}}}$: independent random walks, the exclusion process, and the inclusion process. Particles are allowed to switch their jump rate (the rate identifies the type of particle) between 1 (fast particles) and $\epsilon \in [0,1]$ (slow particles). The switch between the two jump rates happens at rate $\gamma \in (0,\infty )$. In the exclusion process, the interaction is such that each site can be occupied by at most one particle of each type. In the inclusion process, the interaction takes places between particles of the same type at different sites and between particles of different type at the same site. We derive the macroscopic limit equations for the three systems, obtained after scaling space by $N^{-1}$, time by $N^2$, the switching rate by $N^{-2}$, and letting $N\rightarrow \infty$. The limit equations for the macroscopic densities associated to the fast and slow particles is the well-studied double diffusivity model. This system of reaction-diffusion equations was introduced to model polycrystal diffusion and dislocation pipe diffusion, with the goal to overcome the limitations imposed by Fick’s law. In order to investigate the microscopic out-of-equilibrium properties, we analyse the system on $[N]=\{1,\ldots ,N\}$, adding boundary reservoirs at sites 1 and N of fast and slow particles, respectively. Inside [N] particles move as before, but now particles are injected and absorbed at sites 1 and N with prescribed rates that depend on the particle type. We compute the steady-state density profile and the steady-state current. It turns out that uphill diffusion is possible, i.e., the total flow can be in the direction of increasing total density. This phenomenon, which cannot occur in a single-type particle system, is a violation of Fick’s law made possible by the switching between types. We rescale the microscopic steady-state density profile and steady-state current and obtain the steady-state solution of a boundary-value problem for the double diffusivity model.

1 Introduction

Section 1.1 provides the background and the motivation for the paper. Section 1.2 defines the model. Section 1.3 identifies the dual and the stationary measures. Section 1.4 gives a brief outline of the remainder of the paper.

1.1 Background and Motivation

Interacting particle systems are used to model and analyse properties of non-equilibrium systems, such as macroscopic profiles, long-range correlations and macroscopic large deviations. Some models have additional structure, such as duality or integrability properties, which allow for a study of the fine details of non-equilibrium steady states, such as microscopic profiles and correlations. Examples include zero-range processes, exclusion processes, and models that fit into the algebraic approach to duality, such as inclusion processes and related diffusion processes, or models of heat conduction, such as the Kipnis-Marchioro-Presutti model [9, 17, 22, 30, 37]. Most of these models have indistinguishable particles of which the total number is conserved, and so the relevant macroscopic quantity is the density of particles.

Turning to more complex models of non-equilibrium, various exclusion processes with multi-type particles have been studied [24, 25, 41], as well as reaction-diffusion processes [7, 8, 18,19,20], where non-linear reaction-diffusion equations are obtained in the hydrodynamic limit, and large deviations around such equations have been analysed. In the present paper, we focus on a reaction-diffusion model that on the one hand is simple enough so that via duality a complete microscopic analysis of the non-equilibrium profiles can be carried out, but on the other hand exhibits interesting phenomena, such as uphill diffusion and boundary-layer effects. In our model we have two types of particles, fast and slow, that jump at rate 1 and $\epsilon \in [0,1]$, respectively. Particles of identical type are allowed to interact via exclusion or inclusion. There is no interaction between particles of different type that are at different sites. Each particle can change type at a rate that is adapted to the particle interaction (exclusion or inclusion), and is therefore interacting with particles of different type at the same site. An alternative and equivalent view is to consider two layers of particles, where the layer determines the jump rate (rate 1 for the bottom layer, rate $\epsilon$ for the top layer) and where on each layer the particles move according to exclusion or inclusion, and to let particles change layer at a rate that is appropriately chosen in accordance with the interaction. In the limit as $\epsilon \downarrow 0$, particles are immobile on the top layer.

We show that the hydrodynamic limit of all three dynamics is a linear reaction-diffusion system known under the name of double diffusivity model, namely,

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t \rho _0 = \Delta \rho _0 + \Upsilon (\rho _1-\rho _0),\\ \partial _t \rho _1 = \epsilon \Delta \rho _1 + \Upsilon (\rho _0-\rho _1), \end{array}\right. } \end{aligned}$$

(1.1)

where $\rho _i$, $i\in \{0,1\}$, are the macroscopic densities of the two types of particles, and $\Upsilon \in (0,\infty )$ is the scaled switching rate. The above system was introduced in [1] to model polycrystal diffusion (more generally, diffusion in inhomogeneous porous media) and dislocation pipe diffusion, with the goal to overcome the restrictions imposed by Fick’s law. Non-Fick behaviour is immediate from the fact that the total density $\rho =\rho _0+\rho _1$ does not satisfy the classical diffusion equation.

The double diffusivity model was studied extensively in the PDE literature [2, 33, 35], while its discrete counterpart was analysed in terms of a single random walk switching between two layers [34]. The same macroscopic model was studied independently in the mathematical finance literature in the context of switching diffusion processes [49]. Thus, we have a family of interacting particle systems whose macroscopic limit is relevant in several distinct contexts. Another context our three dynamics fit into are models of interacting active random walks with an internal state that changes randomly (e.g. activity, internal energy) and that determines their diffusion rate and or drift [3, 16, 28, 32, 38, 39, 44, 46].

An additional motivation to study two-layer models comes from population genetics. Individuals live in colonies, carry different genetics types, and can be either active or dormant. While active, individuals resample by adopting the type of a randomly sampled individual in the same colony, and migrate between colonies by hopping around. Active individuals can become dormant, after which they suspend resampling and migration, until they become active again. Dormant individuals reside in what is called a seed bank. The overall effect of dormancy is that extinction of types is slowed down, and so genetic diversity is enhanced by the presence of the seed bank. A wealth of phenomena can occur, depending on the parameters that control the rates of resampling, migration, falling asleep and waking up [6, 31]. Dormancy not only affects the long-term behaviour of the population quantitatively. It may also lead to qualitatively different equilibria and time scales of convergence. For a panoramic view on the role of dormancy in the life sciences, we refer the reader to [42].

From the point of view of non-equilibrium systems driven by boundary reservoirs, switching interacting particle systems have not been studied. On the one hand, such systems have both reaction and diffusion and therefore exhibit a richer non-equilibrium behaviour. On the other hand, the macroscopic equations are linear and exactly solvable in one dimension, and so these systems are simple enough to make a detailed microscopic analysis possible. As explained above, the system can be viewed as an interacting particle system on two layers. Therefore duality properties are available, which allows for a detailed analysis of the system coupled to reservoirs, which is dual to an absorbing system. In one dimension the analysis of the microscopic density profile reduces to a computation of the absorption probabilities of a simple random walk on a two-layer system absorbed at the left and right boundaries. From the analytic solution we can identify both the density profile and the current in the system. This leads to two interesting phenomena. The first phenomenon is uphill diffusion (see e.g. [12,13,14, 21, 40]), i.e., in a well-defined parameter regime the current can go against the particle density gradient: when the total density of particles at the left end is higher than at the right end, the current can still go from right to left. The second phenomenon is boundary-layer behaviour: in the limit as $\epsilon \downarrow 0$, in the macroscopic stationary profile the densities in the top and bottom layer are equal, which for unequal boundary conditions in the top and bottom layer results in a discontinuity in the stationary profile. Corresponding to this jump in the macroscopic system, we identify a boundary layer in the microscopic system of size $\sqrt{\epsilon }\,\log (1/\epsilon )$ where the densities are unequal. The quantification of the size of this boundary layer is an interesting corollary of the exact macroscopic stationary profile that we obtain from the microscopic system via duality.

1.2 Three Models

For $\sigma \in \{-1,0,1\}$ we introduce an interacting particle system on ${{\mathbb {Z}}}$ where the particles randomly switch their jump rate between two possible values, 1 and $\epsilon$, with $\epsilon \in [0,1]$. For $\sigma =-1$ the particles are subject to the exclusion interaction, for $\sigma =0$ the particles are independent, while for $\sigma =1$ the particles are subject to the inclusion interaction. Let

$$\begin{aligned} \begin{aligned} \eta _0(x)&:= \text {number of particles at site } x \text { jumping at rate } 1,\\ \eta _1(x)&:= \text {number of particles at site } x \text { jumping at rate } \epsilon . \end{aligned} \end{aligned}$$

The configuration of the system is

$$\begin{aligned} \eta := \{\eta (x)\}_{x\in {{\mathbb {Z}}}} \in {\mathcal {X}} = {\left\{ \begin{array}{ll} \{0,1\}^{{\mathbb {Z}}}\times \{0,1\}^{{\mathbb {Z}}}, &{}\text {if }\sigma =-1,\\ {{\mathbb {N}}}_0^{{{\mathbb {Z}}}}\times {{\mathbb {N}}}_0^{{{\mathbb {Z}}}}, &{}\text {if }\sigma =0,1, \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned} \eta (x) := (\eta _0(x),\eta _1(x)), \qquad x \in {{\mathbb {Z}}}. \end{aligned}$$

We call $\eta _0=\{\eta _0(x)\}_{x\in {{\mathbb {Z}}}}$ and $\eta _1=\{\eta _1(x)\}_{x\in {{\mathbb {Z}}}}$ the configurations of fast particles, respectively, slow particles. When $\epsilon = 0$ we speak of dormant particles (see Fig. 1).

Fig. 1

Two equivalent representations of switching independent random walks ($\sigma =0$)

Definition 1.1

(Switching interacting particle systems) For $\epsilon \in [0,1]$ and $\gamma \in (0,\infty )$, let $L_{\epsilon ,\gamma }$ be the generator

$$\begin{aligned} \begin{aligned} L_{\epsilon ,\gamma } := L_0 +\epsilon L_1 + \gamma L_{0 \updownarrow 1}, \end{aligned} \end{aligned}$$

(1.2)

acting on bounded cylindrical functions $f:{\mathcal {X}}\rightarrow {{\mathbb {R}}}$ as

$$\begin{aligned} \begin{aligned} (L_0 f)(\eta )&= \sum _{|x-y|=1} \Big \{\eta _0(x)(1+\sigma \eta _0(y))\,\big [f((\eta _0-\delta _x+\delta _y,\eta _1))-f(\eta )\big ]\\[-0.2cm]&\quad + \eta _0(y)(1+\sigma \eta _0(x))\,\big [f((\eta _0+\delta _x-\delta _y,\eta _1))-f(\eta )\big ]\Big \},\\[0.2cm] (L_1 f)(\eta )&= \sum _{|x-y|=1} \Big \{\eta _1(x)(1+\sigma \eta _1(y))\,\big [f((\eta _0,\eta _1-\delta _x+\delta _y))-f(\eta )\big ]\\[-0.2cm]&\quad + \eta _1(y)(1+\sigma \eta _1(x))\, \big [f((\eta _0,\eta _1+\delta _x-\delta _y))-f(\eta )\big ]\Big \},\\[0.2cm] (L_{0 \updownarrow 1}f)(\eta )&= \gamma \sum _{x\in {{\mathbb {Z}}}^d} \Big \{\eta _0(x)(1+\sigma \eta _1(x))\, \big [f((\eta _0-\delta _x,\eta _1+\delta _x))-f(\eta )\big ]\\&\quad +\eta _1(x)(1+\sigma \eta _0(x))\, \big [f((\eta _0+\delta _x,\eta _1-\delta _x))-f(\eta )\big ]\Big \}. \end{aligned} \end{aligned}$$

The Markov process $\{\eta (t):\,t\ge 0\}$ on state space ${\mathcal {X}}$ with

$$\begin{aligned} \eta (t) := \{\eta (x,t)\}_{x\in {{\mathbb {Z}}}} = \big \{(\eta _0(x,t),\eta _1(x,t))\big \}_{x\in {{\mathbb {Z}}}}, \end{aligned}$$

hopping rates $1,\epsilon$ and switching rate $\gamma$ is called switching exclusion process for $\sigma =-1$, switching random walks for $\sigma =0$ (see Fig. 1), and switching inclusion process for $\sigma =1$.

$\square$

1.3 Duality and Stationary Measures

The systems defined in (1.2) can be equivalently formulated as jump processes on the graph (see Fig. 1) with vertex set $\{(x,i) \in {{\mathbb {Z}}}^d \times I\}$, with $I = \{0,1\}$ labelling the two layers, and edge set given by the nearest-neighbour relation

$$\begin{aligned} (x,i)\sim (y,j) \quad \text { when } \quad {\left\{ \begin{array}{ll} |x-y|=1 \text { and } i=j,\\ x=y \text { and } |i-j| =1. \end{array}\right. } \end{aligned}$$

In this formulation the particle configuration is

$$\begin{aligned} \eta =(\eta _i(x))_{(x,i)\in {{\mathbb {Z}}}\times I} \end{aligned}$$

and the generator L is given by

$$\begin{aligned} \begin{aligned} (Lf)(\eta )&= \sum _{i\in I}\sum _{|x-y|=1}\epsilon ^i\eta _i(x) (1+\sigma \eta _i(y))\,[f(\eta -\delta _{(x,i)}+\delta _{(y,i)})-f(\eta )]\\&\quad +\epsilon ^i\eta _i(y) (1+\sigma \eta _i(x))\,[f (\eta -\delta _{(y,i)}+\delta _{(x,i)})-f(\eta )]\\&\quad +\sum _{i\in I}\gamma \sum _{x\in {{\mathbb {Z}}}} \eta _i(x)(1+\sigma \eta _{1-i})\,[f(\eta -\delta _{(x,i)}+\delta _{(x,1-i)}) -f(\eta )]. \end{aligned} \end{aligned}$$

(1.3)

Thus, a single particle (when no other particles are present) is subject to two movements:

• (i) Horizontal movement In layer $i=0$ and $i=1$ the particle performs a nearest-neighbour random walk on ${{\mathbb {Z}}}$ at rate 1, respectively, $\epsilon$.

• (ii) Vertical movement The particle switches layer at the same site at rate $\gamma$.

It is well known (see e.g. [47]) that for these systems there exists a one-parameter family of reversible product measures

$$\begin{aligned} \big \{\mu _\theta =\bigotimes _{(x,i)\in {{\mathbb {Z}}}\times I}\nu _{(x,i),\theta }:\, \theta \in \Theta \big \} \end{aligned}$$

with $\Theta =[0,1]$ if $\sigma =-1$ and $\Theta =[0,\infty )$ if $\sigma \in \{0,1\}$, and with marginals given by

$$\begin{aligned} \nu _{(x,i),\theta } = {\left\{ \begin{array}{ll} \text {Bernoulli}\,(\theta ), &{}\sigma = -1,\\ \text {Poisson}\,(\theta ), &{}\sigma = 0,\\ \text {Negative--Binomial}\,(1,\tfrac{\theta }{1+\theta }), &{}\sigma = 1. \end{array}\right. } \end{aligned}$$

(1.4)

Moreover, the classical self-duality relation holds, i.e., for all configurations $\eta , \, \xi \in {\mathcal {X}}$ and for all times $t\ge 0$,

$$\begin{aligned} {{\mathbb {E}}}_\eta [D(\xi ,\eta _t)]={{\mathbb {E}}}_\xi [D(\xi _t,\eta )], \end{aligned}$$

with $\{\xi (t): \ t\ge 0\}$ and $\{\eta (t):\ t\ge 0\}$ two copies of the process with generator given in (1.2) and self-duality function $D:\,{\mathcal {X}} \times {\mathcal {X}} \rightarrow {{\mathbb {R}}}$ given by

$$\begin{aligned} D(\xi ,\eta ) := \prod _{(x,i) \in {{\mathbb {Z}}}^d \times I} d(\xi _i(x),\eta _i(x)), \end{aligned}$$

(1.5)

with

$$\begin{aligned} d(k,n) := \frac{n!}{(n-k)!}\frac{1}{w(k)}\,{\mathbf {1}}_{\{k\le n\}} \end{aligned}$$

(1.6)

and

$$\begin{aligned} w(k):= {\left\{ \begin{array}{ll} \frac{\Gamma (1+k)}{\Gamma (1)}, &{}\sigma =1,\\ 1, &{}\sigma =-1,0. \end{array}\right. } \end{aligned}$$

(1.7)

Remark 1.2

(Possible extensions) Note that we could allow for more than two layers, for inhomogeneous rates and for non-nearest neighbour jumps as well, and the same duality relation would still hold (see e.g. [26] for an inhomogeneous version of the exclusion process). More precisely, let $\{\omega _i(\{x,y\})\}_{x,y\in {{\mathbb {Z}}}}$ and $\{\alpha _i(x)\}_{x\in {{\mathbb {Z}}}}$ be collections of bounded weights for $i\in I_M=\{0,1,\ldots , M\}$ with $M<\infty$. Then the interacting particle systems with generator

$$\begin{aligned} \begin{aligned} (L_{D,\gamma }f)(\eta )&=\sum _{i=0}^M D_i \sum _{|x-y|=1} \omega _i(\{x,y\})\,\Big \{\eta _i(x)\,(\alpha _i(y)+\sigma \eta _i(y))\,\big [f(\eta -\delta _{(x,i)}+\delta _{(y,i)})-f(\eta )\big ]\\&\quad + \eta _i(y)\,(\alpha _i(x)+\sigma \eta _i(x))\,\big [f (\eta -\delta _{(y,i)}+\delta _{(x,i)})-f(\eta )\big ]\Big \}\\&\quad + \sum _{i=0}^{M-1} \gamma _{\{i,i+1\}}\,\sum _{x\in {{\mathbb {Z}}}} \Big \{\eta _i(x)\, \big [f(\eta -\delta _{(x,i)}+\delta _{(x,i+1)})-f(\eta )\big ]\\&\quad +\eta _{i+1}(x)\,\big [f(\eta -\delta _{(x,i+1)}+\delta _{(x,i)})-f(\eta )\big ]\Big \}, \end{aligned} \end{aligned}$$

(1.8)

with $\eta =(\eta _i(x))_{(x,i)\in {{\mathbb {Z}}}\times I_M}$, $\{D_i\}_{i\in I_M}$ a bounded decreasing collection of weights in [0, 1] and $\gamma _{\{i,i+1\}}\in (0,\infty )$, are still self-dual with duality function as in (1.5), but with I replaced by $I_M$ and single-site duality functions given by $d_{(x,i)}(k,n)=\frac{n!}{(n-k)!}\frac{1}{w_{(x,i)}(k)}\,{\mathbf {1}}_{\{k\le n\}}$ with

$$\begin{aligned} w_{(x,i)}(k)\ := {\left\{ \begin{array}{ll} \frac{\alpha _i(x)!}{(\alpha _i(x)-k)!}\mathbb {1}_{\{k \le \alpha _i(x)\}}, &{}\sigma = -1,\\ \alpha _i(x)^k, &{}\sigma = 0,\\ \frac{\Gamma (\alpha _i(x)+k)}{\Gamma (\alpha _i(x))}, &{}\sigma = 1. \end{array}\right. } \end{aligned}$$

In the present paper we prefer to stick to the two-layer homogeneous setting in order not to introduce extra notations. However, it is straightforward to extend many of our results to the inhomogeneous multi-layer model.$\square$

Duality is a key tool in the study of detailed properties of interacting particle systems, since it allows for explicit computations. It has been used widely in the literature (see, e.g., [20, 43]). In the next section, self-duality (which implies microscopic closure of the evolution equation for the empirical density field) will be used to derive the hydrodynamic limit of the switching interacting particle systems described above. More precisely, we will use self-duality with one and two dual particles to compute the expectation of the evolution of the occupation variables and of the two-point correlations. These are needed, respectively, to control the expectation and the variance of the density field.

1.4 Outline

Section 2 identifies and analyses the hydrodynamic limit of the system in Definition 1.1 after scaling space, time and switching rate diffusively. In doing so, we exhibit a class of interacting particle systems whose microscopic dynamics scales to a macroscopic dynamics called the double diffusivity model. We provide a discussion on the solutions of this model, thereby connecting mathematical literature applied to material science and to financial mathematics. Section 3 looks at what happens, both microscopically and macroscopically, when boundary reservoirs are added, resulting in a non-equilibrium flow. Here the possibility of uphill diffusion becomes manifest, which is absent in single-layer systems, i.e., the two layers interact in a way that allows for a violation of Fick’s law. We characterise the parameter regime for uphill diffusion. We show that, in the limit as $\epsilon \downarrow 0$, the macroscopic stationary profile of the type-1 particles adapts to the microscopic stationary profile of the type-0 particles, resulting in a discontinuity at the boundary for the case of unequal boundary conditions on the top layer and the bottom layer. Appendix A provides the inverse of a certain boundary-layer matrix.

2 The Hydrodynamic Limit

In this section we scale space, time and switching diffusively, so as to obtain a hydrodynamic limit. In Sect. 2.1 we scale space by 1/N, time by $N^2$, the switching rate by $1/N^2$, introduce scaled microscopic empirical distributions, and let $N\rightarrow \infty$ to obtain a system of macroscopic equations. In Sect. 2.2 we recall some known results for this system, namely, there exists a unique solution that can be represented in terms of an underlying diffusion equation or, alternatively, via a Feynman-Kac formula involving the switching diffusion process.

2.1 From Microscopic to Macroscopic

Let $N \in {{\mathbb {N}}}$, and consider the scaled generator $L_{\epsilon ,\gamma _N}$ (recall (1.2)) with $\gamma _N = \Upsilon /N^2$ for some $\Upsilon \in (0,\infty )$, i.e., the reaction term is slowed down by a factor $N^2$ in anticipation of the diffusive scaling we are going to consider.

In order to study the collective behaviour of the particles after scaling of space and time, we introduce the following empirical density fields, which are Radon measure-valued cádlág (i.e., right-continuous with left limits) processes:

$$\begin{aligned} {\mathsf {X}}^{N}_0(t) := \frac{1}{N} \sum _{x\in {{\mathbb {Z}}}} \eta _{0}(x,tN^2)\,\delta _{x/N},\qquad {\mathsf {X}}^{N}_1(t) := \frac{1}{N} \sum _{x\in {{\mathbb {Z}}}} \eta _{1}(x,tN^2)\,\delta _{x/N}, \end{aligned}$$

where $\delta _y$ stands for the Dirac measure at $y\in {{\mathbb {R}}}$.

In order to derive the hydrodynamic limit for the switching interacting particle systems, we need the following set of assumptions. In the following we denote by $C^\infty _c({{\mathbb {R}}})$ the space of infinitely differentiable functions with values in ${{\mathbb {R}}}$ and compact support, by $C_b({{\mathbb {R}}};\sigma )$ the space of bounded and continuous functions with values in ${{\mathbb {R}}}_+$ for $\sigma \in \{0,1\}$ and with values in [0, 1] for $\sigma =-1$, by $C_0({{\mathbb {R}}})$ the space of continuous functions vanishing at infinity, by $C^2_0({{\mathbb {R}}})$ the space of twice differentiable functions vanishing at infinity and by M the space of Radon measure on ${{\mathbb {R}}}$.

Assumption 2.1

(Compatible initial conditions) Let ${\bar{\rho }}_i\in C_b({{\mathbb {R}}};\sigma )$ for $i\in \{0,1\}$ be two given functions, called initial macroscopic profiles. We say that a sequence $(\mu _N)_{N\in {{\mathbb {N}}}}$ of measures on ${\mathcal {X}}$ is a sequence of compatible initial conditions when:

• (i) For any $i\in \{0,1\}$, $g\in C^\infty _c({{\mathbb {R}}})$ and $\delta >0,$

  $$\begin{aligned} \lim _{N\rightarrow \infty }\mu _N\left( \left| \langle {\mathsf {X}}^{N}_i(0),g\rangle - \int _{{\mathbb {R}}}\mathrm{d}x\ {\bar{\rho }}_i(x)g(x) \right| >\delta \right) =0. \end{aligned}$$

• (ii) There exists a constant $C<\infty$ such that

  $$\begin{aligned} \sup _{(x,i) \in {{\mathbb {Z}}}\times I} {{\mathbb {E}}}_{\mu _N}[\eta _i(x)^2] \le C. \end{aligned}$$

  (2.1)

$\square$

Note that Assumption 2.1(ii) is the same as employed in [11, Theorem 1, Assumption (b)] and is trivial for the exclusion process.

Theorem 2.2

(Hydrodynamic scaling) Let ${\bar{\rho }}_0,{\bar{\rho }}_1 \in C_b({{\mathbb {R}}};\sigma )$ be two initial macroscopic profiles, and let $(\mu _N)_{N\in {{\mathbb {N}}}}$ be a sequence of compatible initial conditions. Let ${{\mathbb {P}}}_{\mu _N}$ be the law of the measure-valued process

$$\begin{aligned} \{X^N(t):\,t \ge 0\} , \qquad X^N(t) := (X_0^N(t), X_1^N(t)), \end{aligned}$$

induced by the initial measure $\mu _N$. Then, for any $T, \delta >0$ and $g\in C^\infty _c({{\mathbb {R}}})$,

$$\begin{aligned} \lim _{N\rightarrow \infty }{{\mathbb {P}}}_{\mu _N}\left( \sup _{t\in [0,T]} \left| \,\langle {\mathsf {X}}^{N}_i(t),g\rangle - \int _{{\mathbb {R}}}\mathrm{d}x\, \rho _i(x,t)g(x)\,\right| >\delta \right) =0, \qquad i \in I, \end{aligned}$$

where $\rho _0$ and $\rho _1$ are the unique continuous and bounded strong solutions of the system

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t \rho _0 = \Delta \rho _0 + \Upsilon (\rho _1-\rho _0),\\ \partial _t \rho _1 = \epsilon \Delta \rho _1 + \Upsilon (\rho _0-\rho _1), \end{array}\right. } \end{aligned}$$

(2.2)

with initial conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} \rho _0(x,0) = {\bar{\rho }}_0(x),\\ \rho _1(x,0) = {\bar{\rho }}_1(x). \end{array}\right. } \end{aligned}$$

(2.3)

Proof

The proof follows the standard route presented in [48, Section 8] (see also [11, 20]). We still explain the main steps because the two-layer setup is not standard. First of all, note that the macroscopic equation (2.2) can be straightforwardly identified by computing the action of the rescaled generator $L^N = L_{\epsilon ,\Upsilon /N^2}$ on the cylindrical functions $f_i(\eta ):=\eta _i(x), \ i\in \{0,1\}$, namely ,

$$\begin{aligned} (L^N f_i)(\eta ) = \epsilon ^i \left[ \eta _i(x+1)-2\eta _i(x)+\eta _i(x-1)\right] + \frac{\Upsilon }{N^2}\left[ \eta _{1-i}(x)-\eta _i(x)\right] \end{aligned}$$

and hence, for any $g\in C^{\infty }_c({{\mathbb {R}}})$,

$$\begin{aligned} \begin{aligned}&\int _0^{tN^2} \mathrm{d}s\,L^N(\langle {\mathsf {X}}^{N}_i(s),g\rangle ) \\&\quad = \int _0^{tN^2}\mathrm{d}s\, \frac{\epsilon ^i}{N} \sum _{x\in {{\mathbb {Z}}}} \eta _i(x,s)\, \tfrac{1}{2}\,\big [g((x+1)/N)-2g(x/N)+g((x-1)/N)\big ]\\&\qquad +\int _0^{tN^2} \mathrm{d}s\,\frac{1}{N} \sum _{x\in {{\mathbb {Z}}}} g(x/N)\, \frac{\Upsilon }{N^2}\,\big [\eta _{1-i}(x,s)-\eta _i(x,s)\big ], \end{aligned} \end{aligned}$$

where we moved the generator of the simple random walk to the test function by using reversibility w.r.t. the counting measure. By the regularity of g, we thus have

$$\begin{aligned} \begin{aligned}&\int _0^{tN^2} \mathrm{d}s\,L^N(\langle {\mathsf {X}}^{N}_i(s),g\rangle ) \\&\quad = \int _0^{t}\mathrm{d}s\, \langle {\mathsf {X}}^{N}_i(sN^2),\epsilon ^i \Delta g\rangle +\int _0^{tN^2} \mathrm{d}s\, \frac{\Upsilon }{N^2}\, \big [\langle {\mathsf {X}}^{N}_{1-i}(s),g\rangle -\langle {\mathsf {X}}^{N}_i(s),g\rangle \big ]+ o(\tfrac{1}{N^2}), \end{aligned} \end{aligned}$$

which is the discrete counterpart of the weak formulation of the right-hand side of (2.2), i.e., $\int _0^t\mathrm{d}s\int _{{\mathbb {R}}}\mathrm{d}x$ $\rho _{i}(x,s)\Delta g(x) + \Upsilon \int _0^t\mathrm{d}s\int _{{\mathbb {R}}}\mathrm{d}x\, [\rho _{1-i}(x,s)-\rho _i(x,s)]\,g(x)$. Thus, as a first step, we show that

$$\begin{aligned}&\lim _{N\rightarrow \infty }{{\mathbb {P}}}_{\mu _N}\left( \sup _{t\in [0,T]}\left| \langle {\mathsf {X}}^{N}_i(t),g\rangle - \langle {\mathsf {X}}^{N}_i(0),g\rangle - \int _0^{t}\mathrm{d}s\, \langle {\mathsf {X}}^{N}_i(sN^2),\epsilon ^i\Delta g\rangle \right. \right. \\&\quad \left. \left. -\int _0^{tN^2} \mathrm{d}s\, \frac{\Upsilon }{N^2}\,\big [\langle {\mathsf {X}}^{N}_{1-i}(s)-{\mathsf {X}}^{N}_i(s),g\rangle \big ] \right| >\delta \right) =0. \end{aligned}$$

In order to prove the above convergence we employ the Dynkin’s martingale formula for Markov processes (see, e.g., [48, Theorem 4.8]), which gives that the process defined as

$$\begin{aligned} M^N_i(g,t):= \langle {\mathsf {X}}^{N}_i(t),g\rangle - \langle {\mathsf {X}}^{N}_i(0),g\rangle -\int _0^{tN^2} \mathrm{d}s\,L^N(\langle {\mathsf {X}}^{N}_i(s),g\rangle ) \end{aligned}$$

is a martingale w.r.t. the natural filtration generated by the process $\{\eta _t\}_{t\ge 0}$ and with predictable quadratic variation expressed in terms of the carré du champ, i.e.,

$$\begin{aligned} \langle M^N_i(g,t), M^N_i(g,t) \rangle = \int _0^t \mathrm{d}s\,{{\mathbb {E}}}_{\mu _N}\left[ \Gamma ^N_i(g,s) \right] \end{aligned}$$

with

$$\begin{aligned} \Gamma ^N_i(g,s) =L^N \left( \langle {\mathsf {X}}^{N}_i(s),g\rangle \ \right) ^2 -\langle {\mathsf {X}}^{N}_i(s),g\rangle L^N \left( \langle {\mathsf {X}}^{N}_i(s),g\rangle \ \right) . \end{aligned}$$

We then have, by Chebyshev’s inequality and Doob’s martingale inequality (see, e.g., [36, Section1.3]),

$$\begin{aligned}&{{\mathbb {P}}}_{\mu _N}\left( \sup _{t\in [0,T]}\left| \langle {\mathsf X^{N}_i(s)}, g\rangle - \langle {\mathsf X^{N}_i(s)}, g\rangle - \int _0^{t}\mathrm{d}s\, \langle {\mathsf {X}}^{N}_i(sN^2),\epsilon \Delta g\rangle \right. \right. \nonumber \\&\qquad \left. \left. -\int _0^{tN^2} \mathrm{d}s\, \frac{\Upsilon }{N^2}\,\big [\langle {\mathsf {X}}^{N}_{1-i}(s),g\rangle -\langle {\mathsf {X}}^{N}_i(s),g\rangle \big ] \right| >\delta \right) \end{aligned}$$

(2.4)

$$\begin{aligned}&\quad \le \frac{1}{\delta ^2}{{\mathbb {E}}}_{\mu _N}\left[ \sup _{t\in [0,T]}\left| M^N_i(g,s)\right| ^2 \right] \le \frac{4}{\epsilon ^2}{{\mathbb {E}}}_{\mu _N}\left[ \left| M^N_i(g,T)\right| ^2 \right] \nonumber \\&\quad =\frac{4}{\delta ^2}{{\mathbb {E}}}_{\mu _N}\left[ \langle M^N_i(g,T), M^N_i(g,T) \rangle ^2 \right] \nonumber \\&\quad =\frac{4}{\delta ^2 N^2}{{\mathbb {E}}}_{\mu _N}\left[ \int _0^{N^2T}\mathrm{d}s\,\sum _{x\in {{\mathbb {Z}}}^d}\eta _i(x,s)(1+\sigma \eta _i(x\pm 1,s))\left( g\left( \frac{x\pm 1}{N}\right) -g\left( \frac{x}{N}\right) \right) \right] \nonumber \\&\qquad +\frac{4\Upsilon }{\delta ^2N^4}{{\mathbb {E}}}_{\mu _N}\left[ \int _0^{N^2T} \mathrm{d}s\, \sum _{x\in {{\mathbb {Z}}}^d} (\eta _i(x,s)+\eta _{1-i}(x,s)+2\sigma \eta _i(x,s)\eta _{1-i}(x,s)) g^2\left( \frac{x}{N}\right) \right] , \end{aligned}$$

(2.5)

where in the last equality we explicitly computed the carré du champ. Let $k\in {{\mathbb {N}}}$ be such that the support of g is in $[-k,k]$. Then, by the regularity of g, (2.4) is bounded by

$$\begin{aligned}&\frac{4}{\delta ^2N^2}(N^2T)(2k+1)N \frac{\Vert \nabla g\Vert _{\infty }}{N^2}\sup _{x,\in {{\mathbb {Z}}},s\in [0,N^2T]}{{\mathbb {E}}}_{\mu _N}\left[ \eta _i(x,s)(1+\sigma \eta _i(x + 1,s)) \right] \nonumber \\&\quad +\frac{4\Upsilon }{\delta ^2N^4}(N^2T)(2k+1)N\Vert g \Vert _{\infty }\sup _{x,\in {{\mathbb {Z}}},s\in [0,N^2T]}{{\mathbb {E}}}_{\mu _N}\left[ \eta _i(x,s)+\eta _{1-i}(x,s) \right. \nonumber \\&\qquad \left. +2\sigma \eta _i(x,s)\eta _{1-i}(x,s) \right] . \end{aligned}$$

(2.6)

We now show that, as a consequence of (2.1), for any $(x,i),\ (y,j)\in {{\mathbb {Z}}}\times I,$

$$\begin{aligned} {{\mathbb {E}}}_{\mu _N}\left[ \eta _i(x,s)\right] \le C, \quad {{\mathbb {E}}}_{\mu _N}\left[ \eta _i(x,s) \eta _j(y,s)\right] \le C, \end{aligned}$$

(2.7)

from which we obtain

$$\begin{aligned}&{{\mathbb {P}}}_{\mu _N}\left( \sup _{t\in [0,T]}\left| \langle {\mathsf {X}}^{N}_0(s),g\rangle - \langle {\mathsf {X}}^{N}_0(s),g\rangle - \int _0^{t}\mathrm{d}s\, \langle {\mathsf {X}}^{N}_0(sN^2),\epsilon \Delta g\rangle \right. \right. \nonumber \\ {}&\qquad \left. \left. -\int _0^{tN^2} \mathrm{d}s\, \frac{\Upsilon }{N^2}\,\big [\langle {\mathsf {X}}^{N}_1(s),g\rangle -\langle {\mathsf {X}}^{N}_0(s),g\rangle \big ] \right| >\delta \right) \nonumber \\&\quad \le \frac{8T}{\delta ^2N}(2k+1)\Vert \nabla g\Vert _{\infty }C+\Upsilon \frac{16 T}{\delta ^2N}(2k+1)\Vert g \Vert _{\infty } C, \end{aligned}$$

(2.8)

and the desired convergence follows. In order to prove (2.7), first of all note that, by the Cauchy-Schwartz inequality, it follows from (2.1) that, for any $(x,i),\ (y,j)\in {{\mathbb {Z}}}\times I$,

$$\begin{aligned} {{\mathbb {E}}}_{\mu _N}\left[ \eta _i(x)\eta _j(y) \right] \le C. \end{aligned}$$

(2.9)

Moreover, recalling the duality functions given in (1.5) and defining the configuration $\xi =\delta _{(x,i)}+\delta _{(y,j)}$ for $(x,i)\ne (y,j)$, we have that $D(\xi ,\eta _t)=\eta _i(x,t)\eta _j(y,t)$ and thus, using the classical self-duality relation,

$$\begin{aligned}&{{\mathbb {E}}}_{\mu _N}\left[ \eta _i(x,t)\eta _j(y,t) \right] ={{\mathbb {E}}}_{\mu _N}[D(\xi ,\eta _t)]=\int _{{\mathcal {X}}} {{\mathbb {E}}}_\eta [D(\xi ,\eta _t)]\,\mathrm{d}\mu _N(\eta )\\ {}&=\int _{{\mathcal {X}}} {{\mathbb {E}}}_\xi [D(\xi _t,\eta )]\,\mathrm{d}\mu _N(\eta )={{\mathbb {E}}}_\xi \left[ {{\mathbb {E}}}_{\mu _N}[D(\xi _t,\eta )] \right] . \end{aligned}$$

Labeling the particles in the dual configuration as $(X_t,i_t)$ and $(Y_t,j_t)$ with initial conditions $(X_0,i_0)=(x,i)$ and $(Y_0,j_0)=(y,j)$, we obtain

$$\begin{aligned}&{{\mathbb {E}}}_{\mu _N}\left[ \eta _i(x,t)\eta _j(y,t) \right] \nonumber \\&\quad ={{\mathbb {E}}}_\xi \left[ {{\mathbb {E}}}_{\mu _N}[\eta _{i_t}(X_t)\eta _{j_t}(Y_t) \mathbb {1} _{(X_t,i_t)\ne (Y_t,j_t)}] +{{\mathbb {E}}}_{\mu _N}[\eta _{i_t}(X_t)(\eta _{i_t}(X_t)-1) \mathbb {1} _{(X_t,i_t)=(Y_t,j_t)}] \right] \nonumber \\&\quad \le {{\mathbb {E}}}_\xi \left[ {{\mathbb {E}}}_{\mu _N}[\eta _{i_t}(X_t)\eta _{j_t}(Y_t)] \right] \le {{\mathbb {E}}}_\xi \left[ \sup _{(x,i),(y,j)\in {{\mathbb {Z}}}\times \{0,1\}} {{\mathbb {E}}}_{\mu _N}[\eta _{i}(x)\eta _{j}(y)] \right] \le C, \end{aligned}$$

(2.10)

where we used (2.9) in the last inequality. Similarly, for $\xi =\delta _{(x,i)}$ and $(X_t,i_t)$ the dual particle with initial condition $(X_0,i_0)=(x,i)$, we have that ${{\mathbb {E}}}_{\mu _N}\left[ \eta _i(x,t) \right] \le {{\mathbb {E}}}_{\mu _N}\left[ D(\xi ,\eta _t )\right] ={{\mathbb {E}}}_\xi [ {{\mathbb {E}}}_{\mu _N} [\eta _{i_t}(X_t) ] ]$. Using that $\eta _i(x)\le \eta _i(x)^2$ for any $(x,i)\in {{\mathbb {Z}}}\times I$ and using (2.1), we obtain (2.7). The proof is concluded after showing the following:

• (i) Tightness holds for the sequence of distributions of the processes $\{{\mathsf {X}}^N_i\}_{N\in {{\mathbb {N}}}}$, denoted by $\{Q_N\}_{N\in {{\mathbb {N}}}}$.

• (ii) All limit points coincide and are supported by the unique path ${\mathsf {X}} _i(t, \mathrm{d}x)=\rho _i(x,t)\,\mathrm{d}x$, with $\rho _i$ the unique weak (and in particular strong) bounded and continuous solution of (2.2).

While for (i) we provide an explanation, we skip the proof of (ii) because it is standard and is based on PDE arguments, namely, the existence and the uniqueness of the solutions in the class of continuous-time functions with values in $C_b({{\mathbb {R}}},\sigma )$ (we refer to [48, Lemma 8.6 and 8.7] for further details), and the fact that Assumption 2.1(i) ensures that the initial condition of (2.2) is also matched.

Tightness of the sequence $\{Q_N\}_{N\in {{\mathbb {N}}}}$ follows from the compact containment condition on the one hand, i.e., for any $\delta >0$ and $t>0$ there exists a compact set $K\subset M$ such that ${{\mathbb {P}}}_{\mu _N}(X^N_i\in K)>1-\delta$, and the equi-continuity condition on the other hand, i.e., $\limsup _{N\rightarrow \infty }{{\mathbb {P}}}_{\mu _N}( \omega ({\mathsf {X}}_i^N,\delta ,T))\ge {\mathfrak {e}})\le {\mathfrak {e}}$ for $\omega (\alpha ,\delta ,T):=\sup \{ d_M(\alpha (s),\alpha (t)): s,t\in [0,T], |s-t|\le \delta \}$ with $d_M$ the metric on Radon measures defined as

$$\begin{aligned} d_M(\nu _1,\nu _2):=\sum _{j\in {{\mathbb {N}}}}2^{-j}\left( 1 \wedge \left| \int _{{\mathbb {R}}}\phi _j \mathrm{d}\nu _1 -\int _{{\mathbb {R}}}\phi _j \mathrm{d}\nu _2 \right| \right) \end{aligned}$$

for an appropriately chosen sequence of functions $( \phi _j )_{j\in {{\mathbb {N}}}}$ in $C^{\infty }_c({{\mathbb {R}}})$. We refer to [48, Section A.10] for details on the above metric and to the proof of [48, Lemma 8.5] for the equi-continuity condition. We conclude by proving the compact containment condition. Define

$$\begin{aligned} K:=\Big \{ \nu \in M\ s.t. \ \exists \, k\in {{\mathbb {N}}}\ s.t. \ \nu [-\ell ,\ell ]\le A(2\ell +1)\ell ^2 \ \forall \ \ell \in [k,\infty ]\cap {{\mathbb {N}}}\Big \} \end{aligned}$$

with $A>0$ such that $\frac{C\pi }{6A}<\delta$. By [48, Proposition A.25], we have that K is a pre-compact subset of M. Moreover, by the Markov inequality and Assumption 2.1(ii), it follows that

$$\begin{aligned} Q_N({{\bar{K}}}^c)&\le \sum _{\ell \in {{\mathbb {N}}}}{{\mathbb {P}}}_{\mu _N}\left( {\mathsf {X}}_i^N([-\ell ,\ell ])\ge A(2\ell +1)\ell ^2 \right) \le \sum _{\ell \in {{\mathbb {N}}}}\frac{1}{ A(2\ell +1)\ell ^2 } {{\mathbb {E}}}_{\mu _N}\left[ {\mathsf {X}}_i^N([-\ell ,\ell ]) \right] \\&=\sum _{\ell \in {{\mathbb {N}}}}\frac{1}{ A(2\ell +1)\ell ^2 } \sum _{x\in [-\ell ,\ell ]\cap \frac{{{\mathbb {Z}}}}{N}}{{\mathbb {E}}}_{\mu _N}\left[ \eta _i(x, tN^2) \right] \le \sum _{\ell \in {{\mathbb {N}}}} \frac{1}{ A(2\ell +1)\ell ^2 } \frac{2\ell N+1}{N}C \\&\le \frac{C}{A} \sum _{\ell \in {{\mathbb {N}}}} \frac{1}{ \ell ^2 }<\delta , \end{aligned}$$

from which it follows that $Q_N({{\bar{K}}})>1-\delta$ for any N. $\square$

Remark 2.3

(Total density)

• (i) If $\rho _0,\rho _1$ are smooth enough and satisfy (2.2), then by taking extra derivatives we see that the total density $\rho :=\rho _0+\rho _1$ satisfies the thermal telegrapher equation

  $$\begin{aligned} \partial _t \left( \partial _t \rho + 2\Upsilon \rho \right) = - \epsilon \Delta (\Delta \rho ) + (1+\epsilon )\Delta \left( \partial _t \rho + \Upsilon \rho \right) , \end{aligned}$$

  (2.11)

  which is second order in $\partial _t$ and fourth order in $\partial _x$ (see [2, 33] for a derivation). Note that (2.11) shows that the total density does not satisfy the usual diffusion equation. This fact will be investigated in detail in the next section, where we will analyse the non-Fick property of $\rho$.

• (ii) If $\epsilon =1$, then the total density $\rho$ satisfies the heat equation $\partial _t\rho = \Delta \rho$.

• (iii) If $\epsilon =0$, then (2.11) reads

  $$\begin{aligned} \partial _t\left( \partial _t \rho + 2\Upsilon \rho \right) = \Delta \left( \partial _t \rho + \Upsilon \rho \right) , \end{aligned}$$

  which is known as the strongly damped wave equation. The term $\partial _t(2\lambda \rho )$ is referred to as frictional damping, the term $\Delta (\partial _t \rho )$ as Kelvin-Voigt damping (see [10]).

$\square$

Remark 2.4

(Literature) We mention in passing that in [38] hydrodynamic scaling of interacting particles with internal states has been considered in a different setting and with a different methodology. $\square$

2.2 Existence, Uniqueness and Representation of the Solution

The existence and uniqueness of a continuous-time solution $(\rho _0(t),\, \rho _1(t))$ with values in $C_b({{\mathbb {R}}},\sigma )$ of the system in (2.2) can be proved by standard Fourier analysis. Below we recall some known results that have a more probabilistic interpretation.

Stochastic representation of the solution

The system in (2.2) fits in the realm of switching diffusions (see e.g. [49]), which are widely studied in the mathematical finance literature. Indeed, let $\{i_t:\,t \ge 0\}$ be the pure jump process on state space $I=\{0,1\}$ that switches at rate $\Upsilon$, whose generator acting on bounded functions $g:\,I \rightarrow {{\mathbb {R}}}$ is

$$\begin{aligned} (Ag)(i) := \Upsilon (g(1-i)-g(i)), \qquad i \in I. \end{aligned}$$

Let $\{X_t:\,t \ge 0\}$ be the stochastic process on ${{\mathbb {R}}}$ solving the stochastic differential equation

$$\begin{aligned} \mathrm{d}X_t = \psi (i_t)\,\mathrm{d}W_t, \end{aligned}$$

where $W_t=B_{2t}$ with $\{B_t:\, t \ge 0\}$ standard Brownian motion, and $\psi :\,I\rightarrow \{D_0,D_1\}$ is given by

$$\begin{aligned} \psi := D_0\,{\varvec{1}}_{\{0\}} + D_1\,{\varvec{1}}_{\{1\}}, \end{aligned}$$

with $D_0=1$ and $D_1=\epsilon$ in our setting. Let ${\mathcal {L}} = {\mathcal {L}}_{\epsilon ,\Upsilon }$ be the generator defined by

$$\begin{aligned} ({\mathcal {L}} f)(x,i) := \lim _{t\downarrow 0} \frac{1}{t}\,{{\mathbb {E}}}_{x,i}[f(X_t,i_t)-f(x,i)] \end{aligned}$$

for $f:\,{{\mathbb {R}}}\times I \rightarrow {{\mathbb {R}}}$ such that $f(\cdot ,i)\in C^2_0({{\mathbb {R}}})$. Then, via a standard computation (see e.g. [29, Eq.(4.4)]), it follows that

$$\begin{aligned} \begin{aligned} ({\mathcal {L}} f)(x,i)&=\psi (i)(\Delta f)(x,i)+ \Upsilon [f(x,1-i)-f(x,i)]\\[0.2cm]&={\left\{ \begin{array}{ll} \Delta f(x,0)+\Upsilon \,[f(x,1)-f(x,0)], &{}i=0,\\ \epsilon \Delta f(x,1)+\Upsilon \,[f(x,0)-f(x,1)], &{}i=1. \end{array}\right. } \end{aligned} \end{aligned}$$

We therefore have the following result that corresponds to [29, Chapter 5, Section 4, Theorem 4.1](see also [49, Theorem 5.2]).

Theorem 2.5

(Stochastic representation of the solution) Suppose that ${\bar{\rho }}_i:\,{{\mathbb {R}}}\rightarrow {{\mathbb {R}}}$ for $i\in I$ are continuous and bounded. Then (2.2) has a unique solution given by

$$\begin{aligned} \rho _i(x,t)={{\mathbb {E}}}_{(x,i)}[ {\bar{\rho }}_{i_t}(X_t)], \qquad i \in I. \end{aligned}$$

Note that if there is only one particle in the system (1.2), then we are left with a single random walk, say $\{Y_t:\,t \ge 0\}$, whose generator, denoted by ${\mathsf {A}}$, acts on bounded functions $f:\,{{\mathbb {Z}}}\times I\rightarrow {{\mathbb {R}}}$ as

$$\begin{aligned} (\mathsf Af)(y,i) = \psi (i)\left[ \sum _{z\sim y} [f(z,i)-f(y,i)]\right] + \Upsilon \,[f(y,1-i)-f(y,i)]. \end{aligned}$$

After we apply the generator to the function $f(y,i)=y$, we get

$$\begin{aligned} \mathsf (Af)(y,i)=0, \end{aligned}$$

i.e., the position of the random walk is a martingale. Computing the quadratic variation via the carré du champ, we find

$$\begin{aligned} {\mathsf {A}}(Y_t^2) =\psi (i_t) [(Y_t+1)^2-Y_t^2] + \psi (i_t)[(Y_t-1)^2-Y_t^2] = 2\psi (i_t). \end{aligned}$$

Hence the predictable quadratic variation is given by

$$\begin{aligned} \int _0^t \mathrm{d}s\,2\psi (i_s). \end{aligned}$$

Note that for $\epsilon =0$ the latter equals the total amount of time the random walk is not dormant up to time t.

When we diffusively scale the system (scaling the reaction term was done at the beginning of Sect. 2), the quadratic variation becomes

$$\begin{aligned} \int _0^{tN^2} \mathrm{d}s\, \psi (i_{N,s}) = \int _0^{t} \mathrm{d}r\,\psi (i_r). \end{aligned}$$

As a consequence, we have the following invariance principle:

• Given the path of the process $\{i_t:\, t\ge 0\}$,

  $$\begin{aligned} \lim _{N\rightarrow \infty } \frac{Y_{N^2t}}{N} = W_{\int _0^{t} \mathrm{d}r\,\sqrt{\psi (i_r)}}, \end{aligned}$$

  where $W_t=B_{2t}$ with $\{B_t:\, t \ge 0\}$ is standard Brownian motion.

Thus, if we knew the path of the process $\{i_r:\, r\ge 0\}$, then we could express the solution of the system in (2.2) in terms of a time-changed Brownian motion. However, even though $\{i_r:\, r\ge 0\}$ is a simple flipping process, we cannot say much explicitly about the random time $\int _0^{t} \mathrm{d}r\,\sqrt{\psi (i_r)}$. We therefore look for a simpler formula, where the relation to a Brownian motion with different velocities is more explicit. We achieve this by looking at the resolvent of the generator ${\mathcal {L}}$. In the following, we denote by $\{S_t, \, t\ge 0\}$ the semigroup on $C_b({{\mathbb {R}}})$ of $\{W_{t}:\,t\ge 0\}$.

Proposition 2.6

(Resolvent) Let $f:\,{{\mathbb {R}}}\times I\rightarrow {{\mathbb {R}}}$ be a bounded and smooth function. Then, for $\lambda >0$, $\epsilon \in (0,1]$ and $i\in I$,

$$\begin{aligned} \begin{aligned}&(\lambda {\varvec{I}}-{\mathcal {L}})^{-1} f(x,i)\\&\quad =\int _0^\infty \mathrm{d}t\, \frac{1}{\epsilon ^i}\, \mathrm{e}^{-\tfrac{1+\epsilon }{\epsilon }\ell (\Upsilon ,\lambda )t} \left( \cosh (tc_\epsilon (\Upsilon ,\lambda ))+ \frac{1-\epsilon }{\epsilon }\ell _\epsilon (\Upsilon ,\lambda )\frac{\sinh (tc_\epsilon (\Upsilon ,\lambda ))}{c_\epsilon (\lambda )}\right) \,(S_tf(\cdot ,i))(x) \\&\qquad + \int _0^\infty \mathrm{d}t \,\mathrm{e}^{-\tfrac{1+\epsilon }{\epsilon }\ell (\Upsilon ,\lambda )t} \left( \frac{\Upsilon }{\epsilon }\sinh (tc_\epsilon (\Upsilon ,\lambda ))\right) \,(S_tf(\cdot ,1-i))(x) , \end{aligned}\nonumber \\ \end{aligned}$$

(2.12)

where $c_\epsilon (\Upsilon ,\lambda )= \sqrt{\left( \tfrac{1-\epsilon }{\epsilon }\right) ^2\ell (\Upsilon ,\lambda )^2+\frac{\Upsilon ^2}{\epsilon }}$ and $\ell (\Upsilon ,\lambda )=\frac{\Upsilon +\lambda }{2}$, while for $\epsilon =0$,

$$\begin{aligned} (\lambda {\varvec{I}}-{\mathcal {L}})^{-1}f(x,i)=\int _0^\infty \mathrm{d}t\,\mathrm{e}^{-\lambda \tfrac{2\Upsilon +\lambda }{\Upsilon +\lambda }t}\left( \left( \tfrac{\Upsilon }{\lambda +\Upsilon }\right) ^i(S_tf(\cdot ,0))(x)+ \left( \tfrac{\Upsilon }{\Upsilon +\lambda }\right) ^{i+1}(S_tf(\cdot ,1))(x) \right) . \end{aligned}$$

(2.13)

Proof

The proof is split into two parts.

$\underline{{\mathrm{Case}}\,\,\epsilon >0.}$ We can split the generator ${\mathcal {L}}$ as

$$\begin{aligned} {\mathcal {L}} = \psi (i) \tilde{{\mathcal {L}}} = \psi (i)\left( \Delta + \frac{1}{\psi (i)} A\right) = \psi (i)(\Delta + {{\tilde{A}}}), \end{aligned}$$

i.e., we decouple $X_t$ and $i_t$ in the action of the generator. We can now use the Feynman-Kac formula to express the resolvent of the operator ${\mathcal {L}}$ in terms of the operator $\tilde{{\mathcal {L}}}$. Denoting by ${{\tilde{{{\mathbb {E}}}}}}$ the expectation of the process with generator $\tilde{{\mathcal {L}}}$, we have, for $\lambda \in {{\mathbb {R}}}$,

$$\begin{aligned} (\lambda {\varvec{I}}-{\mathcal {L}})^{-1} f(x,i)= & {} \left( \frac{\lambda {\varvec{I}}}{\psi }-\tilde{{\mathcal {L}}} \right) ^{-1}\left( \frac{f(x,i)}{\psi (i)}\right) \\= & {} \int _0^\infty \mathrm{d}t\,\,{\tilde{{{\mathbb {E}}}}}_{(x,i)} \left[ \mathrm{e}^{-\int _{0}^t \mathrm{d}s\, \frac{\lambda }{\psi (i_s)} }\,\, \frac{f(X_t,i_t)}{\psi (i_t)} \right] , \end{aligned}$$

and by the decoupling of $X_t$ and $i_t$ under $\tilde{{\mathcal {L}}}$, we get

$$\begin{aligned} \begin{aligned}&(\lambda {\varvec{I}}-{\mathcal {L}})^{-1} f(x,i)\\&\quad = \int _0^\infty \mathrm{d}t\,\,{\tilde{{{\mathbb {E}}}}}_{i}\left[ \mathrm{e}^{-\lambda \int _{0}^t \mathrm{d}s\,\frac{1}{\psi (i_s)}}\,\, \frac{{\varvec{1}}_{\{0\}}(i_t)}{\psi (i_t)} \right] (S_{t}f(\cdot ,0))(x) \\&\qquad + \int _0^\infty \mathrm{d}t\,\,{\tilde{{{\mathbb {E}}}}}_{i} \left[ \mathrm{e}^{-\lambda \int _{0}^t \frac{1}{\psi (i_s)}}\,\, \frac{{\varvec{1}}_{\{1\}}(i_t)}{\psi (i_t)} \right] (S_{t}f(\cdot ,1))(x)\\&\quad = \int _0^\infty \mathrm{d}t\,\,{\tilde{{{\mathbb {E}}}}}_{i} \left[ \mathrm{e}^{-\lambda \int _{0}^t \mathrm{d}s\, \frac{1}{\psi (i_s)}}\,\, {\varvec{1}}_{\{0\}}(i_t) \right] (S_{t}f(\cdot ,0))(x) \\&\qquad + \frac{1}{\epsilon } \int _0^\infty \mathrm{d}t\,\,{\tilde{{{\mathbb {E}}}}}_{i} \left[ \mathrm{e}^{-\lambda \int _{0}^t \mathrm{d}s\,\frac{1}{\psi (i_s)}}\,\, {\varvec{1}}_{\{1\}}(i_t) \right] (S_{t}f(\cdot ,1))(x). \end{aligned} \end{aligned}$$

Defining

$$\begin{aligned} A:= \left[ \begin{array}{c c c c} -\Upsilon &{} \Upsilon \\ \Upsilon &{} -\Upsilon \\ \end{array} \right] , \qquad \psi _\epsilon := \left[ \begin{array}{c c c c} 1 &{} 0 \\ 0 &{} \epsilon \\ \end{array} \right] , \end{aligned}$$

and using again the Feynman-Kac formula, we have

$$\begin{aligned} (\lambda {\varvec{I}}-{\mathcal {L}})^{-1} \left[ \begin{array}{c c c c} f(x,0) \\ f(x,1) \\ \end{array} \right] = \int _0^\infty \mathrm{d}t\,K_{\epsilon }(t,\lambda ) \left[ \begin{array}{c c c c} (S_tf(\cdot ,0))(x)\\ (S_tf(\cdot ,1))(x) \\ \end{array} \right] \end{aligned}$$

with $K_{\epsilon }(t,\lambda ) = \mathrm{e}^{t\psi _\epsilon ^{-1}(-\lambda {\varvec{I}} +A)}\psi _\epsilon ^{-1}$.

Using the explicit formula for the exponential of a $2\times 2$ matrix (see e.g. [4, Corollary 2.4]), we obtain

$$\begin{aligned}&\mathrm{e}^{t\psi _\epsilon ^{-1}(-\lambda {\varvec{I}} +A)} =\mathrm{e}^{-\tfrac{1+\epsilon }{\epsilon }\ell (\Upsilon ,\lambda )t}\nonumber \\&\quad \times \left[ \begin{array}{c c c c} \cosh (tc_\epsilon (\Upsilon ,\lambda ))+ \tfrac{1-\epsilon }{\epsilon }\ell (\Upsilon ,\lambda )\tfrac{\sinh (tc_\epsilon (\Upsilon ,\lambda ))}{c_\epsilon (\Upsilon ,\lambda )}&{} \Upsilon \tfrac{\sinh (tc_\epsilon (\Upsilon ,\lambda ))}{c_\epsilon (\Upsilon ,\lambda )} \\ \tfrac{\Upsilon }{\epsilon }\tfrac{\sinh (tc_\epsilon (\Upsilon ,\lambda ))}{c_\epsilon (\Upsilon ,\lambda )} &{}\cosh (tc_\epsilon (\Upsilon ,\lambda ))- \tfrac{1-\epsilon }{\epsilon }\ell (\Upsilon ,\lambda )\tfrac{\sinh (tc_\epsilon (\Upsilon ,\lambda ))}{c_\epsilon (\Upsilon ,\lambda )}\\ \end{array} \right] \nonumber \\ \end{aligned}$$

(2.14)

with $c_\epsilon (\Upsilon ,\lambda )= \sqrt{\left( \tfrac{1-\epsilon }{\epsilon }\right) ^2\ell (\Upsilon ,\lambda )^2+\frac{\Upsilon ^2}{\epsilon }}$ and $\ell (\Upsilon ,\lambda )=\frac{\Upsilon +\lambda }{2}$, from which we obtain (2.12).

$\underline{{\mathrm{Case}}\,\,\epsilon =0.}$ We derive $K_0(t,\lambda )$ by taking the limit $\epsilon \downarrow 0$ in the previous expression, i.e., $K_0(t,\lambda )=\lim _{\epsilon \downarrow 0}$ $K_\epsilon (t,\lambda )$. We thus have that $K_0(t,\lambda )$ is equal to

$$\begin{aligned}&\lim _{\epsilon \downarrow 0}\mathrm{e}^{-\tfrac{1+\epsilon }{\epsilon }\ell (\Upsilon ,\lambda )t}\left[ \begin{array}{c c c c} \cosh (tc_\epsilon (\Upsilon ,\lambda ))+ \tfrac{1-\epsilon }{\epsilon }\ell (\Upsilon ,\lambda )\tfrac{\sinh (tc_\epsilon (\Upsilon ,\lambda ))}{c_\epsilon (\Upsilon ,\lambda )}&{} \tfrac{\Upsilon }{\epsilon }\tfrac{\sinh (tc_\epsilon (\Upsilon ,\lambda ))}{c_\epsilon (\Upsilon ,\lambda )} \\ \tfrac{\Upsilon }{\epsilon }\tfrac{\sinh (tc_\epsilon (\Upsilon ,\lambda ))}{c_\epsilon (\Upsilon ,\lambda )} &{}\tfrac{1}{\epsilon }\cosh (tc_\epsilon (\Upsilon ,\lambda ))- \tfrac{1-\epsilon }{\epsilon ^2}\ell (\Upsilon ,\lambda )\tfrac{\sinh (tc_\epsilon (\Upsilon ,\lambda ))}{c_\epsilon (\Upsilon ,\lambda )}\\ \end{array} \right] \\&\quad =\mathrm{e}^{-\lambda \tfrac{2\Upsilon +\lambda }{\Upsilon +\lambda }t}\left[ \begin{array}{c c c c} 1&{} \tfrac{\Upsilon }{\Upsilon +\lambda } \\ \tfrac{\Upsilon }{\Upsilon +\lambda } &{}\left( \tfrac{\Upsilon }{\Upsilon +\lambda }\right) ^2 \\ \end{array} \right] , \end{aligned}$$

from which (2.12) follows. $\square$

Remark 2.7

(Symmetric layers) Note that for $\epsilon =1$ we have

$$\begin{aligned} (\lambda {\varvec{I}}-{\mathcal {L}})^{-1} f(x,i) =\int _0^\infty \mathrm{d}t\, \mathrm{e}^{-\lambda t} \left( \tfrac{1+\mathrm{e}^{-2\Upsilon t}}{2}\,(S_tf(\cdot ,i))(x)+ \tfrac{1-\mathrm{e}^{-2\Upsilon t}}{2}\,(S_tf(\cdot ,1-i))(x)\right) . \end{aligned}$$

$\square$

We conclude this section by noting that the system in (2.2) was studied in detail in [2, 33]. By taking Fourier and Laplace transforms and inverting them, it is possible to deduce explicitly the solution, which is expressed in terms of solutions to the classical heat equation. More precisely, using formula [33, Eq.2.2], we have that

$$\begin{aligned} \rho _0(x,t)= & {} \mathrm{e}^{-\Upsilon t}\,(S_t\,{\bar{\rho }}_0)(x) +\frac{\Upsilon }{1-\epsilon }\mathrm{e}^{-\Upsilon t}\int _{\epsilon t}^t \mathrm{d}s\, \left( \left( \frac{s-\epsilon t}{t-s}\right) ^{1/2}I_1(\upsilon (s))\,(S_s\,{\bar{\rho }}_0)(x) \right. \nonumber \\&\left. +I_0(\upsilon (s))\,(S_s\,{\bar{\rho }}_1)(x)\right) \end{aligned}$$

(2.15)

and

$$\begin{aligned} \rho _1(x,t)= & {} \mathrm{e}^{-\Upsilon t}(S_{\epsilon t}\,{\bar{\rho }}_1)(x) +\frac{\Upsilon }{1-\epsilon } \mathrm{e}^{-\sigma t}\int _{\epsilon t}^t \mathrm{d}s\,\left( \left( \frac{s-\epsilon t}{t-s}\right) ^{-1/2}I_1(\upsilon (s))\, (S_s\,{\bar{\rho }}_1)(x) \right. \nonumber \\&\left. +I_0(\upsilon (s))\,(S_s\,{\bar{\rho }}_0)(x) \right) , \end{aligned}$$

(2.16)

where $\upsilon (s)=\frac{2\Upsilon }{1-\epsilon }((t-s)(s-\epsilon t))^{1/2}$, and $I_0(\cdot )$ and $I_1(\cdot )$ are the modified Bessel functions.

3 The System with Boundary Reservoirs

In this section we consider a finite version of the switching interacting particle systems introduced in Definition 1.1 to which boundary reservoirs are added. Section 3.1 defines the model. Section 3.2 identifies the dual and the stationary measures. Section 3.3 derives the non-equilibrium density profile, both for the microscopic system and the macroscopic system, and offers various simulations. In Sect. 3.4 we compute the stationary horizontal current of slow and fast particles both for the microscopic system and the macroscopic system. Section 3.5 shows that in the macroscopic system, for certain choices of the rates, there can be a flow of particles uphill, i.e., against the gradient imposed by the reservoirs. Thus, as a consequence of the competing driving mechanisms of slow and fast particles, we can have a flow of particles from the side with lower density to the side with higher density.

3.1 Model

We consider the same system as in Definition 1.1, but restricted to $V:=\{1,\ldots ,N\}\subset {{\mathbb {Z}}}$. In addition, we set ${\hat{V}} := V\cup \{L,R\}$ and attach a left-reservoir to L and a right-reservoir to R, both for fast and slow particles. To be more precise, there are four reservoirs (see Fig. 2):

Fig. 2

Case $\sigma =0$, $\epsilon >0$ with boundary reservoirs: two equivalent representations

• (i) For the fast particles, a left-reservoir at L injects fast particles at $x=1$ at rate $\rho _{L,0}(1+\sigma \eta _0(1,t))$ and a right-reservoir at R injects fast particles at $x=N$ at rate $\rho _{R,0}(1+\sigma \eta _0(N,t))$. The left-reservoir absorbs fast particles at rate $1+\sigma \rho _{L,0}$, while the right-reservoir does so at rate $1+\sigma \rho _{R,0}$.

• (ii) For the slow particles, a left-reservoir at L injects slow particles at $x=1$ at rate $\rho _{L,1}(1+\sigma \eta _1(1,t))$ and a right-reservoir at R injects slow particles at $x=N$ at rate $\rho _{R,1}(1+\sigma \eta _1(N,t))$. The left-reservoir absorbs fast particles at rate $1+\sigma \rho _{L,1}$, while the right-reservoir does so at rate $1+\sigma \rho _{R,1}$.

Inside V, the particles move as before.

For $i\in I$, $x \in V$ and $t\ge 0$, let $\eta _{i}(x,t)$ denote the number of particles in layer i at site x at time t. For $\sigma \in \{-1,0,1\}$, the Markov process $\{\eta (t):\,t \ge 0\}$ with

$$\begin{aligned} \eta (t) = \{\eta _{0}(x,t),\eta _{1}(x,t)\}_{x \in V} \end{aligned}$$

has state space

$$\begin{aligned} {\mathcal {X}} = {\left\{ \begin{array}{ll} \{0,1\}^V\times \{0,1\}^V, &{}\sigma =-1,\\ {{\mathbb {N}}}_0^{V}\times {{\mathbb {N}}}_0^{V}, &{}\sigma =0,1,\ \end{array}\right. } \end{aligned}$$

and generator

$$\begin{aligned} L := L_{\epsilon ,\gamma ,N}= L^{\mathrm {bulk}} + L^{\mathrm {res}} \end{aligned}$$

(3.1)

with

$$\begin{aligned}&L^{\mathrm {bulk}}:= L^{\mathrm {bulk}}_0 +\epsilon L^{\mathrm {bulk}}_1 + \gamma L^{\mathrm {bulk}}_{0 \updownarrow 1} \end{aligned}$$

(3.2)

acting on bounded cylindrical functions $f:\,{\mathcal {X}}\rightarrow {{\mathbb {R}}}$ as

$$\begin{aligned} (L^{\mathrm {bulk}}_0 f)(\eta )&=\sum _{x=1}^{N-1} \Big \{\eta _0(x)(1+\sigma \eta _0(x+1))\,\big [f(\eta _0-\delta _{x} +\delta _{x+1},\eta _1)-f(\eta _0,\eta _1)\big ]\\&\quad +\eta _0(x+1)(1+\sigma \eta _0(x))\,\big [f(\eta _0-\delta _{x+1}+\delta _{x},\eta )-f(\eta _0,\eta _1)\big ]\Big \}, \\ (L^{\mathrm {bulk}}_1 f)(\eta )&= \sum _{x=1}^{N-1} \Big \{\eta _1(x)(1+\sigma \eta _1(x+1))\, \big [f(\eta _0,\eta _1-\delta _{x}+\delta _{x+1})-f(\eta _0,\eta _1)\big ]\\&\quad + \eta _1(x+1)(1+\sigma \eta _1(x))\,\big [f(\eta _0,\eta _1-\delta _{x+1}+\delta _{x})-f(\eta _0,\eta _1))\big ]\Big \}, \\ (L^{\mathrm {bulk}}_{0 \updownarrow 1}f)(\eta )&= \sum _{x=1}^N \Big \{\eta _0(x)(1+\sigma \eta _1(x))\, \big [f(\eta _0-\delta _{x},\eta _{1}+\delta _{x})-f(\eta _0,\eta _1)\big ]\\&\quad + \eta _1(x)(1+\sigma \eta _0(x))\,\big [f(\eta _{0}+\delta _{x},\eta _{1}-\delta _{x})-f(\eta _{0},\eta _{1}))\big ]\Big \}, \end{aligned}$$

and

$$\begin{aligned} L^{\mathrm {res}}:=L^{\mathrm {res}}_0+ L^{\mathrm {res}}_1 \end{aligned}$$

(3.3)

acting as

$$\begin{aligned} (L^{\mathrm {res}}_0f)(\eta )&= \eta _0(1)(1+\sigma \rho _{L,0})\,\big [f(\eta _0-\delta _{1},\eta _{1})-f(\eta _0,\eta _{1})\big ]\\&\quad + \rho _{L,0}(1+\sigma \eta _0(1))\,\big [f(\eta _0+\delta _{1},\eta _{1})-f(\eta _0,\eta _{1})\big ]\\&\quad +\eta _0(N)(1+\sigma \rho _{R,0})\,\big [f(\eta _0-\delta _{N},\eta _{1})-f(\eta _0,\eta _{1})\big ] \\&\quad + \rho _{R,0}(1+\sigma \eta _0(N))\,\big [f(\eta _0+\delta _{N},\eta )-f(\eta _0,\eta _{1})\big ], \\ (L^{\mathrm {res}}_1f)(\eta )&=\eta _1(1)(1+\sigma \rho _{L,1})\,\big [f(\eta _{0},\eta _1-\delta _{1})-f(\eta _0,\eta _{1})\big ]\\&\quad +\rho _{L,1}(1+\sigma \eta _1(1))\,\big [f(\eta _{0},\eta _1+\delta _{1})-f(\eta _{0},\eta _{1})\big ]\\&\quad +\eta _1(N)(1+\sigma \rho _{R,1})\,\big [f(\eta _{0},\eta _1-\delta _{N})-f(\eta _0,\eta _{1})\big ] \\&\quad + \rho _{R,1}(1+\sigma \rho _{R,N})\,\big [f(\eta _{0},\eta _1+\delta _{N})-f(\eta _0,\eta _{1})\big ]. \end{aligned}$$

3.2 Duality

In [9] it was shown that the partial exclusion process, a system of independent random walks and the symmetric inclusion processes on a finite set V, coupled with proper left and right reservoirs, are dual to the same particle system but with the reservoirs replaced by absorbing sites. As remarked in [27], the same result holds for more general geometries, consisting of inhomogeneous rates (site and edge dependent), and for many proper reservoirs. Our model is a particular instance of the case treated in [27, Remark 2.2]), because we can think of the rate as conductances attached to the edges.

More precisely, we consider the system where particles jump on two copies of

$$\begin{aligned} {{\hat{V}}}:= V\cup \{L,R\} \end{aligned}$$

and follow the same dynamics as before in V, but with the reservoirs at L and R absorbing. We denote by $\xi$ the configuration

$$\begin{aligned} \xi =(\xi _0,\xi _1):=(\{\xi _0(x)\}_{x\in {{\hat{V}}}},\{\xi _1(x)\}_{x\in {{\hat{V}}}}), \end{aligned}$$

where $\xi _i(x)$ denotes the number of particles at site x in layer i. The state space is $\hat{{\mathcal {X}}} = {{\mathbb {N}}}_0^{{{\hat{V}}}}\times {{\mathbb {N}}}_0^{{{\hat{V}}}}$, and the generator is

$$\begin{aligned} {{\hat{L}}} := {\hat{L}}_{\epsilon ,\gamma ,N} = {{\hat{L}}}^{\mathrm {bulk}} + {{\hat{L}}}^{L,R} \end{aligned}$$

(3.4)

with

$$\begin{aligned}&{{\hat{L}}}^{\mathrm {bulk}}:= {{\hat{L}}}_0^{\mathrm {bulk}}+\epsilon {{\hat{L}}}_1^{\mathrm {bulk}} + \gamma {{\hat{L}}}^{\mathrm {bulk}}_{0 \updownarrow 1} \end{aligned}$$

acting on cylindrical functions $f:\,{\mathcal {X}} \rightarrow {{\mathbb {R}}}$ as

$$\begin{aligned} ({{\hat{L}}}_0^{\mathrm {bulk}}f)(\xi )&=\sum _{x=1}^{N-1} \Big \{\xi _0(x)(1+\sigma \xi _0(x+1))\, \big [f(\xi _0-\delta _{x}+\delta _{x+1},\xi _1)-f(\xi _0,\xi _1)\big ]\\&\quad + \xi _0(x+1)(1+\sigma \xi _0(x))\,\big [f(\xi _0-\delta _{x+1}+\delta _{x},\xi _1)- f(\xi _0,\xi _1)\big ]\Big \},\\ ({{\hat{L}}}_1^{\mathrm {bulk}}f)(\xi )&=\sum _{x=1}^{N-1} \Big \{\xi _1(x)(1+\sigma \xi _1(x+1))\, \big [f(\xi _0,\xi _1-\delta _{x}+\delta _{x+1})-f(\xi _0,\xi _1)\big ]\\&\quad + \xi _1(x+1)(1+\sigma \xi _1(x))\,\big [f(\xi _0,\xi _1-\delta _{x+1}+\delta _{x})-f(\xi _0,\xi _1)\big ]\Big \},\\ ({{\hat{L}}}^{\mathrm {bulk}}_{0 \updownarrow 1}f)(\eta )&=\sum _{x=1}^N \Big \{\xi _0(x)(1+\sigma \xi _1(x))\, \big [f(\xi _0-\delta _{x},\xi _{1}+\delta _{x})-f(\xi _0,\xi _1)\big ]\\&\quad + \xi _1(x)(1+\sigma \xi _0(x))\,\big [f(\xi _{0}+\delta _{x},\xi _{1}-\delta _{x})-f(\xi _{0},\xi _{1})\big ]\Big \}, \end{aligned}$$

and

$$\begin{aligned} {{\hat{L}}}^{L,R}={{\hat{L}}}_0^{L,R}+{{\hat{L}}}_1^{L,R} \end{aligned}$$

acting as

$$\begin{aligned} ({{\hat{L}}}_0^{L,R}f)(\xi )&= \xi _0(1)\,\big [f(\xi _0-\delta _{1},\xi _{1})-f(\xi _0,\xi _{1})\big ] + \xi _0(N)\,\big [f(\xi _0-\delta _{N},\xi _1)-f(\xi _0,\xi _1)\big ],\\ ({{\hat{L}}}_1^{L,R}f)(\xi )&= \xi _1(1)\,\big [f(\xi _0,\xi _1-\delta _{1})-f(\xi _0,\xi _1)\big ] + \xi _1(N)\,\big [f(\xi _0,\xi _1-\delta _{N})-f(\xi _0,\xi _1)\big ]. \end{aligned}$$

Proposition 3.1

(Duality) [9, Theorem 4.1] and [27, Proposition 2.3] The Markov processes

$$\begin{aligned} \{\eta (t):\,t \ge 0\}, \qquad \eta (t)&= \{\eta _0(x,t),\eta _{1}(x,t)\}_{x \in V},\\ \{\xi (t):\,t \ge 0\}, \qquad \xi (t)&= \{\xi _0(x,t),\xi _{1}(x,t)\}_{x \in {{\hat{V}}}}, \end{aligned}$$

with generators L in (3.1) and ${{\hat{L}}}$ in (3.4) are dual. Namely, for all configurations $\eta \in {\mathcal {X}}$, $\xi \in \hat{{\mathcal {X}}}$ and times $t\ge 0$,

$$\begin{aligned} {{\mathbb {E}}}_\eta [ D(\xi ,\eta _t)]= {{\mathbb {E}}}_\xi [ D(\xi _t,\eta )], \end{aligned}$$

where the duality function is given by

$$\begin{aligned} D(\xi ,\eta ):= \left( \prod _{i\in I} d_{(L,i)}(\xi _i(L))\right) \times \left( \prod _{x\in V} d(\xi _i(x),\eta _i(x))\right) \times \left( \prod _{i\in I} d_{(R,i)}(\xi _i(R))\right) , \end{aligned}$$

where, for $k,n\in {{\mathbb {N}}}$ and $i\in I$, $d(\cdot , \cdot )$ is given in (1.6) and

$$\begin{aligned} d_{(L,i)}(k) = \left( \rho _{L,i}\right) ^k, \qquad d_{(R,i)}(k) = \left( \rho _{R,i}\right) ^k. \end{aligned}$$

The proof boils down to checking that the relation

$$\begin{aligned} {{\hat{L}}} D(\cdot ,\eta )(\xi )=LD(\xi ,\cdot )(\eta ) \end{aligned}$$

holds for any $\xi \in {\mathcal {X}}$ and $\xi \in \hat{{\mathcal {X}}}$, as follows from a rewriting of the proof of [9, Theorem 4.1].

Remark 3.2

(Choice of reservoir rates)

• (i) Note that we have chosen the reservoir rates to be 1 both for fast and slow particles. We did this because we view the reservoirs as an external mechanism that injects and absorbs neutral particles, while the particles assume their type as soon as they are in the bulk of the system. In other words, in the present context we view the change of the rate in the two layers as a change of the viscosity properties of the medium is which the particles evolve, instead of a property of the particles themselves.

• (ii) If we would tune the reservoir rate of the slow particles to be $\epsilon$, then the duality relation mentioned above would still holds, with the difference that the dual system would have $\epsilon$ as the rate of absorption for the slow particles. This change of the reservoir rates does not affect our results on the non-Fick properties of the model (see Sect. 3.5 below) and on the size of the boundary layer (see Sect. 3.6 below). Indeed, the limiting macroscopic properties we get by changing the rate of the reservoir of the slow particles are the same as the ones we derive later (i.e., the macroscopic boundary-value problem is the same for any choice of reservoir rate). Note that we do not rescale the reservoir rate when we rescale the system to pass from microscopic to macroscopic, which implies that our macroscopic equation has a Dirichlet boundary condition (see (3.44) below).

$\square$

Also in the context of boundary-driven systems, duality is an essential tool to perform explicit computations. We refer to [37] and [9], where duality for boundary-driven systems was used to compute the stationary profile, by looking at the absorption probabilities of the dual. This is the approach we will follow in the next section. We remark that, for the inclusion process and for generalizations of the exclusion process, duality is the only available tool to characterize properties of the non-equilibrium steady state (such as the stationary profile), whereas other more direct methods (such as the matrix formulation in e.g. [17]) are not applicable in this setting.

3.3 Non-equilibrium Stationary Profile

Also the existence and uniqueness of the non-equilibrium steady state has been established in [27, Theorem 3.3] for general geometries, and the argument in that paper can be easily adapted to our setting.

Theorem 3.3

(Stationary measure) [27, Theorem 3.3(a)] For $\sigma \in \{-1,0,1\}$ there exists a unique stationary measure $\mu _{stat} \$ for $\{\eta (t):\,t \ge 0\}$. Moreover, for $\sigma =0$ and for any values of $\{\rho _{L,0}, \ \rho _{L,1}, \ \rho _{R,0}, \ \rho _{R,1}\}$,

$$\begin{aligned} \mu _{stat} =\prod _{(x,i) \in V \times I} \nu _{(x,i)}, \qquad \nu _{(x,i)} = \mathrm {Poisson}(\theta _{(x,i)}), \end{aligned}$$

(3.5)

while, for $\sigma \in \{-1,1\}$, $\mu _{stat}$ is in general not in product form, unless $\rho _{L,0}= \rho _{L,1}=\rho _{R,0}= \rho _{R,1}$, for which

$$\begin{aligned} \mu _{stat} =\prod _{(x,i) \in V \times I} \nu _{(x,i), \theta }, \end{aligned}$$

(3.6)

where $\nu _{(x,i), \theta }$ is given in (1.4).

Proof

For $\sigma =-1$, the existence and uniqueness of the stationary measure is trivial by the irreducibility and the finiteness of the state space of the process. For $\sigma \in \{0,1\}$, recall from [27, Appendix A] that a probability measure $\mu$ on ${\mathcal {X}}$ is said to be tempered if it is characterized by the integrals $\big \{{{\mathbb {E}}}_\mu [D(\xi ,\eta )]\,:\,\ \xi \in \hat{{\mathcal {X}}} \big \}$ and that if there exists a $\theta \in [0,\infty )$ such that ${{\mathbb {E}}}_\mu [ D(\xi ,\eta )]\le \theta ^{|\xi |}$ for any $\xi \in \hat{{\mathcal {X}}}$. By means of duality we have that, for any $\eta \in {\mathcal {X}}$ and $\xi \in \hat{{\mathcal {X}}}$,

$$\begin{aligned}&\lim _{t\rightarrow \infty }{{\mathbb {E}}}_\eta [D(\xi ,\eta _t)]=\lim _{t\rightarrow \infty }{\hat{{{\mathbb {E}}}}}_\xi [D(\xi _t,\eta )]\nonumber \\&\quad = \sum _{i_0=0}^{|\xi |}\sum _{i_{0,L}=0}^{i_0}\sum _{j_{1,L}=0}^{|\xi |-i_0} \rho _{L,0}^{i_{0,L}}\ \rho _{R,0}^{i_0-i_{0,L}}\ \rho _{L,1}^{i_{1,L}}\ \rho _{R,1}^{|\xi |-i_{0}-i_{1,L}} \end{aligned}$$

(3.7)

$$\begin{aligned}&\qquad \times {\hat{{{\mathbb {P}}}}}_\xi \left( \xi _\infty = i_{0,L}\delta _{(L,0)}+(i_0-i_{0,L})\delta _{(R,0)} + i_{1,L} \delta _{(L,1)}+ (|\xi |-i_{0}-i_{1,L}) \delta _{(R,1)}\right) , \end{aligned}$$

(3.8)

from which we conclude that $\lim _{t\rightarrow \infty }{{\mathbb {E}}}_\eta [D(\xi ,\eta _t)]\le \max \{\rho _{L,0}, \rho _{R,0}, \rho _{L,1}, \rho _{R,1} \}^{|\xi |}$. Let $\mu _s$ be the unique tempered probability measure such that for any $\xi \in \hat{{\mathcal {X}}},$ ${{\mathbb {E}}}_{\mu _{stat}}[D(\xi ,\eta )]$ coincides with (3.7). From the convergence of the marginal moments in (3.7) we conclude that, for any $f:{\mathcal {X}}\rightarrow {{\mathbb {R}}}$ bounded and for any $\eta \in {\mathcal {X}}$,

$$\begin{aligned} \lim _{t\rightarrow \infty }{{\mathbb {E}}}_\eta [f(\eta _t)]={{\mathbb {E}}}_{\mu _{stat}}[f(\eta )]. \end{aligned}$$

Thus, a dominated convergence argument yields that for any probability measure $\mu$ on ${\mathcal {X}}$,

$$\begin{aligned} \lim _{t\rightarrow \infty }{{\mathbb {E}}}_\mu [f(\eta _t)]={{\mathbb {E}}}_{\mu _{stat}}[f(\eta )], \end{aligned}$$

giving that $\mu _{stat}$ is the unique stationary measure. The explicit expression in (3.5) and (3.6) follows from similar computations as in [9], while, arguing by contradiction as in the proof of [27, Theorem 3.3], we can show that the two-point truncated correlations are non-zero for $\sigma \in \{-1,1\}$ whenever at least two reservoir parameters are different. $\square$

3.3.1 Stationary Microscopic Profile and Absorption Probability

In this section we provide an explicit expression for the stationary microscopic density of each type of particle. To this end, let $\mu _{stat}$ be the unique non-equilibrium stationary measure of the process

$$\begin{aligned} \{\eta (t):\,t \ge 0\}, \qquad \eta (t) := \{\eta _0(x,t),\eta _{1}(x,t)\}_{x\in V}, \end{aligned}$$

and let $\{\theta _0({x}),\theta _1({x})\}_{x\in V}$ be the stationary microscopic profile, i.e., for $x\in V$ and $i\in I$,

$$\begin{aligned} \theta _i({x})={{\mathbb {E}}}_{\mu _{stat}}[\eta _i(x,t)]. \end{aligned}$$

(3.9)

Write ${{\mathbb {P}}}_\xi$ (and ${{\mathbb {E}}}_\xi$) to denote the law (and the expectation) of the dual Markov process

$$\begin{aligned} \{\xi (t):\,t \ge 0\}, \qquad \xi (t):=\{\xi _0(x,t),\xi _{1}(x,t)\}_{x\in {{\hat{V}}}}, \end{aligned}$$

starting from $\xi =\{\xi _{0}(x),\xi _{1}(x)\}_{x\in {{\hat{V}}}}$. For $x\in V$, set

$$\begin{aligned} \begin{aligned} \vec {p}_x&:= \big [ \begin{array}{c c c c} {{\hat{p}}}(\delta _{(x,0)}, \delta _{(L,0)})&{{\hat{p}}}(\delta _{(x,0)}, \delta _{(L,1)})&{{\hat{p}}}(\delta _{(x,0)}, \delta _{(R,0)})&{{\hat{p}}}(\delta _{(x,0)}, \delta _{(R,1)}) \end{array} \big ]^T,\\ \vec {q}_x&:=\big [ \begin{array}{c c c c} {{\hat{p}}}(\delta _{(x,1)}, \delta _{(L,0)})&{{\hat{p}}}(\delta _{(x,1)}, \delta _{(L,1)})&{{\hat{p}}}(\delta _{(x,1)}, \delta _{(R,0)})&{{\hat{p}}}(\delta _{(x,1)}, \delta _{(R,1)}) \end{array} \big ]^T, \end{aligned} \end{aligned}$$

(3.10)

where

$$\begin{aligned}&{{\hat{p}}}(\xi , {\tilde{\xi }})=\lim \limits _{t\rightarrow \infty }{{\mathbb {P}}}_\xi (\xi (t) ={\tilde{\xi }}),\quad \nonumber \\&\quad \xi =\delta _{(x,i)} \text { for some } (x,i)\in V\times I,\ \tilde{\xi }\in \{\delta _{(L,0)},\delta _{(L,1)},\delta _{(R,0)},\delta _{(R,1)}\}, \end{aligned}$$

(3.11)

and let

$$\begin{aligned} \vec {\rho } :=\big [ \begin{array}{c c c c} \rho _{(L,0)}&\rho _{(L,1)}&\rho _{(R,0)}&\rho _{(R,1)} \end{array} \big ]^T. \end{aligned}$$

(3.12)

Note that ${{\hat{p}}}(\delta _{(x,i)}, \cdot )$ is the probability of the dual process, starting from a single particle at site x at layer $i\in I$, of being absorbed at one of the four reservoirs. Using Proposition 3.1 and Theorem 3.3, we obtain the following.

Corollary 3.4

(Dual representation of stationary profile) For $x\in V$, the microscopic stationary profile is given by

$$\begin{aligned} \begin{aligned} \theta _0(x)&= \vec {p}_x\, \cdot \,\vec {\rho },\\ \theta _1(x)&= \vec {q}_x\, \cdot \, \vec {\rho }, \end{aligned} \qquad x\in \{1,\ldots ,N\}, \end{aligned}$$

(3.13)

where $\vec {p}_x,\vec {q}_x$ and $\vec {\rho }$ are as in (3.10)–(3.12).

We next compute the absorption probabilities associated to the dual process in order to obtain a more explicit expression for the stationary microscopic profile $\{\theta _0({x}),\theta _1({x})\}_{x\in V}$. The absorption probabilities ${\hat{p}}(\cdot \,,\cdot )$ of the dual process satisfy

$$\begin{aligned} ({{\hat{L}}} {{\hat{p}}})(\cdot , {\tilde{\xi }})(\xi ) = 0\qquad \forall \,\xi \in \hat{{\mathcal {X}}}, \end{aligned}$$

where ${{\hat{L}}}$ is the dual generator defined in (3.4), i.e., they are harmonic functions for the generator ${\hat{L}}$.

In matrix form, the above translates into the following systems of equations:

$$\begin{aligned} \begin{aligned} \vec {p}_1&= \frac{1}{2 + \gamma }\,(\vec {p}_0+\vec {p}_2)+\frac{\gamma }{2+\gamma }\,\vec {q}_1,\\ \vec {q}_1&= \frac{\epsilon }{(1+\epsilon )+\gamma }\,\vec {q}_2+\frac{1}{(1+\epsilon )+\gamma }\,\vec {q}_0 +\frac{\gamma }{(1+\epsilon )+\gamma }\,\vec {p}_1,\\ \vec {p}_x&= \frac{1}{2+\gamma }\,(\vec {p}_{x-1}+\vec {p}_{x+1})+\frac{\gamma }{2+\gamma }\,\vec {q}_x,&x \in \{2, \ldots , N-1\},\\ \vec {q}_x&= \frac{\epsilon }{2\epsilon +\gamma }\,(\vec {q}_{x-1}+\vec {q}_{x+1}) +\frac{\gamma }{2\epsilon +\gamma }\,\vec {p}_x,&x \in \{2, \ldots , N-1\},\\ \vec {p}_N&=\frac{1}{2+\gamma }\,(\vec {p}_{N-1}+\vec {p}_{N+1})+\frac{\gamma }{2+\gamma }\,\vec {q}_N,\\ \vec {q}_N&= \frac{\epsilon }{(1+\epsilon )+\gamma }\,\vec {q}_{N-1} +\frac{1}{(1+\epsilon )+\gamma }\,\vec {q}_{N+1}+\frac{\gamma }{(1+\epsilon )+\gamma }\,\vec {p}_N, \end{aligned} \end{aligned}$$

(3.14)

where

$$\begin{aligned} \begin{aligned}&\vec {p}_0 := \big [ \begin{array}{c c c c} 1&0&0&0 \end{array} \big ]^T,&\vec {q}_{0} :=\big [ \begin{array}{c c c c} 0&1&0&0 \end{array} \big ]^T,\\&\vec {p}_{N+1} := \big [ \begin{array}{c c c c} 0&0&1&0 \end{array} \big ]^T,&\vec {q}_{N+1} := \big [ \begin{array}{c c c c} 0&0&0&1 \end{array} \big ]^T. \end{aligned} \end{aligned}$$

We divide the analysis of the absorption probabilities into two cases: $\epsilon =0$ and $\epsilon >0$.

Case $\epsilon =0$ .

Proposition 3.5

(Absorption probability for $\epsilon =0$) Consider the dual process

$$\begin{aligned} \{\xi (t):\,t \ge 0\}, \qquad \xi (t) = \{\xi _0(x,t),\xi _{1}(x,t)\}_{x \in V}, \end{aligned}$$

with generator ${\hat{L}}_{\epsilon ,\gamma ,N}$ (see (3.4)) with $\epsilon =0$. Then for the dual process, starting from a single particle, the absorption probabilities ${\hat{p}}(\cdot ,\cdot )$ (see (3.11)) are given by

$$\begin{aligned}&\begin{aligned} {{\hat{p}}}(\delta _{(x,0)}, \delta _{(L,0)})&=\frac{1+\gamma }{1+2\gamma }\left( \frac{(1+N)+(1+2N)\,\gamma }{1+N+2N\gamma } -\frac{1+2\gamma }{1+N+2N\gamma }\,x\right) ,\\ {{\hat{p}}}(\delta _{(x,0)}, \delta _{(L,1)})&=\frac{\gamma }{1+2\gamma }\left( \frac{(1+N)+(1+2N)\,\gamma }{1+N+2N\gamma } -\frac{1+2\gamma }{1+N+2N\gamma }\,x\right) ,\\ {{\hat{p}}}(\delta _{(x,0)}, \delta _{(R,0)})&=\frac{1+\gamma }{1+2\gamma }\left( \frac{-\gamma }{1+N+2N\gamma } +\frac{1+2\gamma }{1+N+2N\gamma }\,x\right) ,\\ {{\hat{p}}}(\delta _{(x,0)}, \delta _{(R,1)})&=\frac{\gamma }{1+2\gamma }\left( \frac{-\gamma }{1+N+2N\gamma }+\frac{1+2\gamma }{1+N+2N\gamma }\,x\right) , \end{aligned} \end{aligned}$$

(3.15)

$$\begin{aligned}&\begin{aligned} {{\hat{p}}}(\delta _{(1,1)}, \delta _{(L,0)})&=\frac{\gamma \,(N-\gamma +2N\gamma )}{(1+2\gamma )(1+N+2N\gamma )},\quad \\ {\hat{p}}(\delta _{(1,1)}, \delta _{(L,1)})&=\frac{1+N+(1+3N)\gamma -(1-2N)\gamma ^2}{(1+2\gamma )(1+N+2N\gamma )},\\ {{\hat{p}}}(\delta _{(1,1)}, \delta _{(R,0)})&=\frac{\gamma (1+\gamma )}{(1+2\gamma )(1+N+2N\gamma )},\quad \\ {{\hat{p}}}(\delta _{(1,1)}, \delta _{(R,1)})&=\frac{\gamma ^2}{(1+2\gamma )(1+N+2N\gamma )}, \end{aligned} \end{aligned}$$

(3.16)

and

$$\begin{aligned} {{\hat{p}}}(\delta _{(x,1)}, \delta _{(\beta ,i)}) ={{\hat{p}}}(\delta _{(x,0)}, \delta _{(\beta ,i)}), \qquad x\in \{2,\ldots ,N-1\},\,(\beta ,i)\in \{L,R\}\times I, \end{aligned}$$

(3.17)

and

$$\begin{aligned} \begin{aligned} {{\hat{p}}}(\delta _{(N,1)}, \delta _{(L,0)})&={\hat{p}}(\delta _{(1,1)}, \delta _{(R,0)}),\quad {\hat{p}}(\delta _{(N,1)}, \delta _{(L,1)}) ={\hat{p}}(\delta _{(1,1)}, \delta _{(R,1)}),\\ {{\hat{p}}}(\delta _{(N,1)}, \delta _{(R,0)})&={\hat{p}}(\delta _{(1,1)}, \delta _{(L,0)}),\quad {{\hat{p}}}(\delta _{(N,1)}, \delta _{(R,1)}) ={\hat{p}}(\delta _{(1,1)}, \delta _{(L,1)}). \end{aligned} \end{aligned}$$

(3.18)

Proof

Note that, for $\epsilon =0$, from the linear system in (3.14) we get

$$\begin{aligned} \begin{aligned} \vec {p}_{x+1}-\vec {p}_{x}&=\vec {p}_{x}-\vec {p}_{x-1},\\ \vec {q}_{x}&=\vec {p}_x, \end{aligned} \quad x\in \{2,\ldots ,N-1\}. \end{aligned}$$

(3.19)

Thus, if we set $\vec {c}=\vec {p}_{2}-\vec {p}_{1}$, then it suffices to solve the following 4 linear equations with 4 unknowns $\vec {p}_1,\vec {c},\vec {q}_1$, $\vec {q}_N$:

$$\begin{aligned} \begin{aligned} \vec {p}_1&= \frac{1}{2 + \gamma }\,(\vec {p}_0+\vec {p}_1+\vec {c})+\frac{\gamma }{2+\gamma }\,\vec {q}_1,\\ \vec {q}_1&= \frac{1}{1+\gamma }\,\vec {q}_0 +\frac{\gamma }{1+\gamma }\,\vec {p}_1,\\ \vec {p}_1+(N-1)\vec {c}&=\frac{1}{2+\gamma }\,(\vec {p}_1+(N-2)\vec {c}+\vec {p}_{N+1}) +\frac{\gamma }{2+\gamma }\,\vec {q}_N,\\ \vec {q}_N&= \frac{1}{1+\gamma }\,\vec {q}_{N+1}+\frac{\gamma }{1+\gamma }\,(\vec {p}_1+(N-1)\vec {c}). \end{aligned} \end{aligned}$$

(3.20)

Solving the above equations we get the desired result. $\square$

As a consequence, we obtain the stationary microscopic profile for the original process $\{\eta (t):\,t \ge 0\}, \ \eta (t) = \{\eta _0(x,t),\eta _{1}(x,t)\}_{x \in V}$ when $\epsilon =0$.

Theorem 3.6

(Stationary microscopic profile for $\epsilon =0$) The stationary microscopic profile $\{\theta _0(x),\theta _1(x)\}_{x\in V}$ (see (3.9)) for the process $\{\eta (t):\,t \ge 0\}$ with $\eta (t) = \{\eta _0(x,t),\eta _{1}(x,t)\}_{x \in V}$ with generator $L_{\epsilon ,\gamma ,N}$ (see (3.1)) and $\epsilon =0$ is given by

$$\begin{aligned} \begin{aligned} \theta _0(x)&= \frac{1+\gamma }{1+2\gamma }\left[ \left( \tfrac{(1+N)+(1+2N)\,\gamma }{1+N+2N\gamma } -\tfrac{1+2\gamma }{1+N+2N\gamma }\,x \right) \rho _{L,0} +\left( \tfrac{-\gamma }{1+N+2N\gamma }+\tfrac{1+2\gamma }{1+N+2N\gamma }\,x\right) \rho _{R,0}\right] \\&\qquad +\frac{\gamma }{1+2\gamma }\left[ \left( \tfrac{(1+N)+(1+2N)\,\gamma }{1+N+2N\gamma } -\tfrac{1+2\gamma }{1+N+2N\gamma }\,x\right) \rho _{(L,1)} \right. \\&\left. \qquad +\left( \tfrac{-\gamma }{1+N+2N\gamma }+\tfrac{1+2\gamma }{1+N+2N\gamma }\,x\right) \rho _{(R,1)}\right] \end{aligned} \end{aligned}$$

(3.21)

and

$$\begin{aligned} \begin{aligned} \theta _1(1)&= \frac{\gamma }{1+\gamma }\,\theta _0(1)+\frac{1}{1+\gamma }\,\rho _{(L,1)},\\ \theta _1(x)&=\theta _0(x),&x\in \{2,\ldots ,N-1\},\\ \theta _1(N)&= \frac{\gamma }{1+\gamma }\,\theta _0(N)+\frac{1}{1+\gamma }\,\rho _{(R,1)}. \end{aligned} \end{aligned}$$

(3.22)

Proof

The proof directly follows from Corollary 3.4 and Proposition 3.5. $\square$

Case $\epsilon >0$ .

We next compute the absorption probabilities for the dual process and the stationary microscopic profile for the original process when $\epsilon >0$.

Proposition 3.7

(Absorption probability for $\epsilon >0$) Consider the dual process

$$\begin{aligned} \{\xi (t):\,t \ge 0\}, \qquad \xi (t) = \{\xi _0(x,t),\xi _{1}(x,t)\}_{x \in V}, \end{aligned}$$

with generator ${\hat{L}}_{\epsilon ,\gamma }$ (see (3.4)) with $\epsilon >0$. Let ${\hat{p}}(\cdot ,\cdot )$ (see (3.11)) be the absorption probabilities of the dual process starting from a single particle, and let $(\vec {p}_x,\vec {q}_x)_{x\in V}$ be as defined in (3.10). Then

$$\begin{aligned} \begin{aligned} \vec {p}_x&= \vec {c}_1\, x + \vec {c}_2 + \epsilon (\vec {c}_3\,\alpha _1^x+\vec {c}_4\,\alpha _2^x),\\ \vec {q}_x&= \vec {c}_1\, x + \vec {c}_2 - (\vec {c}_3\,\alpha _1^x+\vec {c}_4\,\alpha _2^x), \end{aligned} \quad x\in V, \end{aligned}$$

(3.23)

where $\alpha _1,\alpha _2$ are the two roots of the equation

$$\begin{aligned} \epsilon \alpha ^2-(\gamma (1+\epsilon )+2\epsilon )\,\alpha +\epsilon =0, \end{aligned}$$

(3.24)

and $\vec {c}_1,\vec {c}_2,\vec {c}_3,\vec {c}_4$ are vectors that depend on the parameters $N,\epsilon ,\alpha _1,\alpha _2$ (see (A.4) for explicit expressions).

Proof

Applying the transformation

$$\begin{aligned} \vec {\tau }_x := \vec {p}_x+\epsilon \vec {q}_x,\qquad \vec {s}_x := \vec {p}_x-\vec {q}_x, \end{aligned}$$

(3.25)

we see that the system in (3.14) decouples in the bulk (i.e., the interior of V), and

$$\begin{aligned} \vec {\tau }_x = \frac{1}{2}(\vec {\tau }_{x+1}+\vec {\tau }_{x-1}),\qquad \vec {s}_x = \frac{\epsilon }{\gamma (1+\epsilon )+2\epsilon }(\vec {s}_{x+1}+\vec {s}_{x-1}), \qquad x\in \{2,\ldots ,N-1\}. \end{aligned}$$

(3.26)

The solution of the above system of recursion equations takes the form

$$\begin{aligned} \vec {\tau }_x = \vec {A}_1 x + \vec {A}_2,\quad \vec {s}_x = \vec {A}_3 \alpha _1^x + \vec {A}_4 \alpha _2^x, \end{aligned}$$

(3.27)

where $\alpha _1,\alpha _2$ are the two roots of the equation

$$\begin{aligned} \epsilon \alpha ^2-(\gamma (1+\epsilon )+2\epsilon )\,\alpha +\epsilon =0. \end{aligned}$$

(3.28)

Rewriting the four boundary conditions in (3.14) in terms of the new transformations, we get

$$\begin{aligned} \big [ \begin{array}{c c c c} \vec {A}_1&\vec {A}_2&\vec {A}_3&\vec {A}_4 \end{array} \big ] = (1+\epsilon )(M_\epsilon ^{-1})^T, \end{aligned}$$

(3.29)

where $M_\epsilon$ is given by

$$\begin{aligned} M_\epsilon := \left[ \begin{array}{c c c c} 0 &{} 1 &{} \epsilon &{} \epsilon \\ 1-\epsilon &{} 1 &{} (\epsilon -1)\alpha _1-\epsilon &{} (\epsilon -1)\alpha _2-\epsilon \\ N+1 &{} 1 &{} \epsilon \alpha _1^{N+1} &{} \epsilon \alpha _2^{N+1}\\ N+\epsilon &{} 1 &{} -\alpha _1^N(\epsilon \alpha _1+(1-\epsilon )) &{} -\alpha _2^N(\epsilon \alpha _2+(1-\epsilon )) \end{array} \right] . \end{aligned}$$

(3.30)

Since $\vec {p}_x = \frac{1}{1+\epsilon }(\vec {\tau }_x+\epsilon \vec {s}_x)$ and $\vec {q}_x = \frac{1}{1+\epsilon }(\vec {\tau }_x-\vec {s}_x)$, by setting

$$\begin{aligned} \vec {c}_i = \frac{1}{1+\epsilon }\vec {A}_i,\quad i\in \{1,2,3,4\}, \end{aligned}$$

we get the desired identities. $\square$

Without loss of generality, from here onwards, we fix the choices of the roots $\alpha _1$ and $\alpha _2$ of the quadratic equation in (3.24) as

$$\begin{aligned} \alpha _1= & {} 1+\frac{\gamma }{2}\left( 1+\frac{1}{\epsilon }\right) -\sqrt{\left[ 1+\frac{\gamma }{2} \left( 1+\frac{1}{\epsilon }\right) \right] ^2-1},\quad \nonumber \\ \alpha _2= & {} 1+\frac{\gamma }{2}\left( 1+\frac{1}{\epsilon }\right) +\sqrt{\left[ 1+\frac{\gamma }{2} \left( 1+\frac{1}{\epsilon }\right) \right] ^2-1}. \end{aligned}$$

(3.31)

Note that, for any $\epsilon , \gamma >0$, we have

$$\begin{aligned} \alpha _1\alpha _2 = 1. \end{aligned}$$

(3.32)

As a corollary, we get the expression for the stationary microscopic profile of the original process.

Theorem 3.8

(Stationary microscopic profile for $\epsilon >0$) The stationary microscopic profile $\{\theta _0(x),\theta _1(x)\}_{x\in V}$ (see (3.9)) for the process $\{\eta (t):\,t \ge 0\}$ and $\eta (t) = \{\eta _0(x,t),\eta _{1}(x,t)\}_{x \in V}$ with generator $L_{\epsilon ,\gamma ,N}$ (see (3.1)) with $\epsilon >0$ is given by

$$\begin{aligned} \begin{aligned} \theta _0(x)&= (\vec {c}_1\,.\,\vec {\rho }) x +(\vec {c}_2\,.\,\vec {\rho })+\epsilon (\vec {c}_3\,.\, \vec {\rho })\alpha _1^x+\epsilon (\vec {c}_4\,.\,\vec {\rho })\alpha _2^x,\\ \theta _1(x)&=(\vec {c}_1\,.\,\vec {\rho }) x +(\vec {c}_2\,.\,\vec {\rho })-(\vec {c}_3\,.\, \vec {\rho })\alpha _1^x-(\vec {c}_4\,.\,\vec {\rho })\alpha _2^x, \end{aligned} \quad x\in V, \end{aligned}$$

(3.33)

where $(\vec {c}_i)_{1\le i \le 4}$ are as in (A.4), and

$$\begin{aligned} \vec {\rho } :=\big [ \begin{array}{c c c c} \rho _{(L,0)}&\rho _{(L,1)}&\rho _{(R,0)}&\rho _{(R,1)} \end{array} \big ]^T. \end{aligned}$$

Proof

The proof follows directly from Corollary 3.4 and Proposition 3.7. $\square$

Remark 3.9

(Symmetric layers) For $\epsilon =1,$ the inverse of the matrix $M_\epsilon$ in the proof of Proposition 3.7 takes a simpler form. This is because for $\epsilon =1$ the system is fully symmetric. In this case, the explicit expression of the stationary microscopic profile is given by

$$\begin{aligned} \begin{aligned} \theta _0(x)&= \frac{1}{2}\left( \frac{N+1-x}{N+1}+ \frac{\alpha _2^{N+1-x}-\alpha _1^{N+1-x}}{\alpha _2^{N+1} -\alpha _1^{N+1}}\right) \rho _{L,0} \\&\quad +\frac{1}{2}\left( \frac{x}{N+1}+ \frac{\alpha _2^x-\alpha _1^x}{\alpha _2^{N+1} -\alpha _1^{N+1}} \right) \rho _{R,0}\\&\quad +\frac{1}{2}\left( \frac{N+1-x}{N+1}- \frac{\alpha _2^{N+1-x}-\alpha _1^{N+1-x}}{\alpha _2^{N+1} \alpha _1^{N+1}} \right) \rho _{(L,1)}\\&\quad +\frac{1}{2}\left( \frac{x}{N+1}- \frac{\alpha _2^x-\alpha _1^x}{\alpha _2^{N+1}-\alpha _1^{N+1}} \right) \rho _{(R,1)} \end{aligned} \end{aligned}$$

(3.34)

and

$$\begin{aligned} \begin{aligned} \theta _1(x)&= \frac{1}{2}\left( \frac{N+1-x}{N+1}- \frac{\alpha _2^{N+1-x}-\alpha _1^{N+1-x}}{\alpha _2^{N+1} -\alpha _1^{N+1}} \right) \rho _{L,0} \\&\quad +\frac{1}{2}\left( \frac{x}{N+1} - \frac{\alpha _2^x-\alpha _1^x}{\alpha _2^{N+1} -\alpha _1^{N+1}} \right) \rho _{R,0}\\&\quad +\frac{1}{2}\left( \frac{N+1-x}{N+1}+ \frac{\alpha _2^{N+1-x}-\alpha _1^{N+1-x}}{\alpha _2^{N+1} -\alpha _1^{N+1}} \right) \rho _{(L,1)} \\&\quad +\frac{1}{2}\left( \frac{x}{N+1}+ \frac{\alpha _2^x-\alpha _1^x}{\alpha _2^{N+1} -\alpha _1^{N+1}} \right) \rho _{(R,1)}. \end{aligned} \end{aligned}$$

(3.35)

However, note that

$$\begin{aligned} \theta _0(x) + \theta _1(x) = 2[(\vec {c}_1.\vec {\rho }) x+(\vec {c}_2.\vec {\rho })]-(1-\epsilon )[(\vec {c}_3\,.\, \vec {\rho })\alpha _1^x-(\vec {c}_4\,.\,\vec {\rho })\alpha _2^x], \end{aligned}$$

which is linear in x only when $\epsilon =1$, and

$$\begin{aligned} \theta _0(x) - \theta _1(x) = (1+\epsilon )[(\vec {c}_3\,.\,\vec {\rho })\alpha _1^x+(\vec {c}_4\,.\,\vec {\rho })\alpha _2^x], \end{aligned}$$

which is purely exponential in x.$\square$

3.3.2 Stationary Macroscopic Profile and Boundary-Value Problem

In this section we rescale the finite-volume system with boundary reservoirs, in the same way as was done for the infinite-volume system in Sect. 2 when we derived the hydrodynamic limit (i.e., space is scaled by 1/N and the switching rate $\gamma _N$ is scaled such that $\gamma _N N^2\rightarrow \Upsilon >0$), and study the validity of Fick’s law at stationarity on macroscopic scale. Before we do that, we justify below that the current scaling of the parameters is indeed the proper choice, in the sense that we obtain non-trivial pointwise limits (macroscopic stationary profiles) of the microscopic stationary profiles found in previous sections, and that the resulting limits (when $\epsilon > 0$) satisfy the stationary boundary-value problem given in (2.2) with boundary conditions $\rho ^{\text {stat}}_0(0) = \rho _{L,0}, \ \rho ^{\text {stat}}_0(1) = \rho _{R,0},\ \rho ^{\text {stat}}_1(0) = \rho _{L,1}$ and $\rho ^{\text {stat}}_1(1) = \rho _{R,1}$.

We say that the macroscopic stationary profiles are given by functions $\rho ^{\text {stat}}_i: (0,1)\rightarrow {{\mathbb {R}}}$ for $i\in I$ if, for any $y\in (0,1)$,

$$\begin{aligned} \lim _{N\rightarrow \infty }\theta _0^{(N)}(\lceil yN\rceil )=\rho ^{\text {stat}}_0(y),\quad \lim _{N\rightarrow \infty } \theta _1^{(N)}(\lceil yN\rceil )=\rho ^{\text {stat}}_1(y). \end{aligned}$$

(3.36)

Theorem 3.10

(Stationary macroscopic profile) Let $(\theta _0^{(N)}(x),\theta _1^{(N)}(x))_{x\in V}$ be the stationary microscopic profile (see (3.9)) for the process $\{\eta (t):\,t \ge 0\}, \ \eta (t) = \{\eta _0(x,t),\eta _{1}(x,t)\}_{x \in V}$ with generator $L_{\epsilon ,\gamma _N,N}$ (see (3.1)), where $\gamma _N$ is such that $\gamma _NN^2\rightarrow \Upsilon$ as $N\rightarrow \infty$ for some $\Upsilon >0$. Then, for each $y\in (0,1)$, the pointwise limits (see Fig. 3)

$$\begin{aligned} {\rho _0^{\mathrm{{stat}}}}(y):=\lim _{N\rightarrow \infty } \theta _0^{(N)}(\lceil yN\rceil ),\quad {\rho _1^{\mathrm{{stat}}}}(y):=\lim _{N\rightarrow \infty } \theta _1^{(N)}(\lceil yN\rceil ), \end{aligned}$$

(3.37)

exist and are given by

$$\begin{aligned} \begin{aligned} {\rho _0^{\mathrm{{stat}}}}(y)&= \rho _{L,0}+(\rho _{R,0}-\rho _{L,0})y,&y\in (0,1),\\ {\rho _1^{\mathrm{{stat}}}}(y)&= {\rho _0^{\mathrm{{stat}}}}(y),&y\in (0,1), \end{aligned} \end{aligned}$$

(3.38)

when $\epsilon =0$, while

$$\begin{aligned}&\begin{aligned} {\rho _0^{\mathrm{{stat}}}}(y)&= \frac{\epsilon }{1+\epsilon }\left[ \frac{\sinh \left[ B_{\epsilon ,\Upsilon }\,(1-y)\right] }{\sinh \left[ B_{\epsilon ,\Upsilon }\right] }\,(\rho _{(L,0)}-\rho _{(L,1)}) +\frac{\sinh \left[ B_{\epsilon ,\Upsilon }\,y\right] }{\sinh \left[ B_{\epsilon ,\Upsilon }\right] }\,(\rho _{(R,0)}-\rho _{(R,1)})\right] \\&\quad + \frac{1}{1+\epsilon }\left[ \rho _{(R,0)}\,y+\rho _{(L,0)} \,(1-y)\right] +\frac{\epsilon }{1+\epsilon } \left[ \rho _{(R,1)}\,y+\rho _{(L,1)} \,(1-y)\right] , \end{aligned} \end{aligned}$$

(3.39)

$$\begin{aligned}&\begin{aligned} {\rho _1^{\mathrm{{stat}}}}(y)&= \frac{1}{1+\epsilon }\left[ \frac{\sinh \left[ B_{\epsilon ,\Upsilon }\,(1-y)\right] }{\sinh \left[ B_{\epsilon ,\Upsilon }\right] }\,(\rho _{(L,1)}-\rho _{(L,0)}) +\frac{\sinh \left[ B_{\epsilon ,\Upsilon }\,y\right] }{\sinh \left[ B_{\epsilon ,\Upsilon }\right] }\,(\rho _{(R,1)}-\rho _{(R,0)})\right] \\&+ \frac{1}{1+\epsilon }\left[ \rho _{(R,0)}\,y+\rho _{(L,0)} \,(1-y)\right] +\frac{\epsilon }{1+\epsilon }\left[ \rho _{(R,1)}\,y+\rho _{(L,1)} \,(1-y)\right] , \end{aligned} \end{aligned}$$

(3.40)

when $\epsilon >0$, where $B_{\epsilon ,\Upsilon }:=\sqrt{\Upsilon (1+\tfrac{1}{\epsilon })}$. Moreover, when $\epsilon >0$, the two limits in (3.37) are uniform in (0, 1).

Proof

For $\epsilon =0$, it easily follows from (3.21) plus the fact that $\gamma _N N^2\rightarrow \Upsilon >0$ and $\tfrac{\lceil yN\rceil }{N}\rightarrow y$ uniformly in (0, 1) as $N\rightarrow \infty$, that

$$\begin{aligned} \lim _{N\rightarrow \infty }\sup _{y\in (0,1)} \left| \theta _0^{(N)}(\lceil yN\rceil )-[\rho _{(L,0)}+(\rho _{(R,0)}-\rho _{(L,0)})\,y]\right| =0, \end{aligned}$$

and since $\theta _1(x) = \theta _0(x)$ for all $x\in \{2,\ldots ,N-1\}$, for fixed $y\in (0,1)$, we have

$$\begin{aligned} \lim _{N\rightarrow \infty } \theta _1^{(N)}(\lceil yN\rceil ) = {\rho _0^{\mathrm{{stat}}}}(y). \end{aligned}$$

When $\epsilon >0,$ since $\gamma _N N^2\rightarrow \Upsilon >0$ as $N\rightarrow \infty ,$ we note the following:

$$\begin{aligned} \begin{aligned}&\gamma _N\overset{N\rightarrow \infty }{\longrightarrow } 0,\\&\quad \lim \limits _{N\rightarrow \infty }\alpha _1=\lim \limits _{N\rightarrow \infty }\alpha _2=1,\\&\quad \lim \limits _{N\rightarrow \infty }\alpha _1^N = \mathrm{e}^{-B_{\epsilon ,\Upsilon }},\quad \lim \limits _{N\rightarrow \infty }\alpha _2^N = \mathrm{e}^{B_{\epsilon ,\Upsilon }}. \end{aligned} \end{aligned}$$

(3.41)

Consequently, from the expressions of $(\vec {c}_i)_{1\le i \le 4}$ defined in (A.4), we also have

$$\begin{aligned} \begin{aligned} \lim \limits _{N\rightarrow \infty }N\vec {c}_1&= \frac{1}{1+\epsilon }\big [ \begin{array}{c c c c} -1&-\epsilon&1&\epsilon \end{array} \big ]^T,\ \lim \limits _{N\rightarrow \infty }\vec {c}_2 = \frac{1}{1+\epsilon }\big [ \begin{array}{c c c c} 1&\epsilon&0&0 \end{array} \big ]^T,\\ \lim \limits _{N\rightarrow \infty }\vec {c}_3&= \frac{1}{1+\epsilon }\big [ \begin{array}{c c c c} \frac{\mathrm{e}^{B_{\epsilon ,\Upsilon }}}{\mathrm{e}^{B_{\epsilon ,\Upsilon }}-\mathrm{e}^{-B_{\epsilon ,\Upsilon }}}&-\frac{\mathrm{e}^{B_{\epsilon ,\Upsilon }}}{\mathrm{e}^{B_{\epsilon ,\Upsilon }}-\mathrm{e}^{-B_{\epsilon ,\Upsilon }}}&-\frac{1}{\mathrm{e}^{B_{\epsilon ,\Upsilon }}-\mathrm{e}^{-B_{\epsilon ,\Upsilon }}}&\frac{1}{\mathrm{e}^{B_{\epsilon ,\Upsilon }}-\mathrm{e}^{-B_{\epsilon ,\Upsilon }}} \end{array} \big ]^T,\\ \lim \limits _{N\rightarrow \infty }\vec {c}_4&= \frac{1}{1+\epsilon }\big [ \begin{array}{c c c c} -\frac{\mathrm{e}^{-B_{\epsilon ,\Upsilon }}}{\mathrm{e}^{B_{\epsilon ,\Upsilon }}-\mathrm{e}^{-B_{\epsilon ,\Upsilon }}}&\frac{\mathrm{e}^{-B_{\epsilon ,\Upsilon }}}{\mathrm{e}^{B_{\epsilon ,\Upsilon }}-\mathrm{e}^{-B_{\epsilon ,\Upsilon }}}&\frac{1}{\mathrm{e}^{B_{\epsilon ,\Upsilon }}-\mathrm{e}^{-B_{\epsilon ,\Upsilon }}}&-\frac{1}{\mathrm{e}^{B_{\epsilon ,\Upsilon }}-\mathrm{e}^{-B_{\epsilon ,\Upsilon }}} \end{array} \big ]^T. \end{aligned} \end{aligned}$$

(3.42)

Combining the above equations with (3.33), and the fact that $\tfrac{\lceil yN\rceil }{N}\rightarrow y$ uniformly in (0, 1) as $N\rightarrow \infty$, we get the desired result. $\square$

Remark 3.11

(Non-uniform convergence) Note that for $\epsilon >0$ both stationary macroscopic profiles, when extended continuously to the closed interval [0, 1], match the prescribed boundary conditions. This is different from what happens for $\epsilon =0$, where the continuous extension of ${\rho _1^{\mathrm{{stat}}}}$ to the closed interval [0, 1] equals ${\rho _0^{\mathrm{{stat}}}}(y)= \rho _{L,0}+(\rho _{R,0}-\rho _{L,0})y$, which does not necessarily match the prescribed boundary conditions unless $\rho _{(L,1)}=\rho _{(L,0)}$ and $\rho _{(R,1)}=\rho _{(R,0)}$. Moreover, as can be seen from the proof above, for $\epsilon >0,$ the convergence of $\theta _i$ to $\rho _i$ is uniform in [0, 1], i.e.,

$$\begin{aligned} \lim _{N\rightarrow \infty }\sup _{y\in [0,1]} \left| \, {\rho _0^{\mathrm{{stat}}}}(y)-\theta _0^{(N)}(\lceil yN\rceil )\,\right| =0,\quad \lim _{N\rightarrow \infty }\sup _{y\in [0,1]} \left| \, {\rho _1^{\mathrm{{stat}}}}(y)-\theta _1^{(N)}(\lceil yN\rceil )\,\right| =0, \end{aligned}$$

while for $\epsilon =0$, the convergence of $\theta _1$ to $\rho _1$ is not uniform in [0, 1] when either $\rho _{(L,0)}\ne \rho _{(L,1)}$ or $\rho _{(R,0)}\ne \rho _{(R,1)}$.

Also, if $\rho _i^{\text {stat}, \epsilon }(\cdot )$ denotes the macroscopic profile defined in (3.39)-(3.40), then for $\epsilon >0$ and $i\in \{0,1\}$, we have

$$\begin{aligned} \lim \limits _{\epsilon \rightarrow 0}\rho _i^{\text {stat}, \epsilon }(y)\rightarrow \rho _i^{\text {stat}, 0}(y) \end{aligned}$$

(3.43)

for fixed $y\in (0,1)$ and $i\in \{0,1\}$, where $\rho _i^{\text {stat}, 0}(\cdot )$ is the corresponding macroscopic profile in (3.38) for $\epsilon =0$. However, this convergence is also not uniform for $i=1$ when $\rho _{(L,0)}\ne \rho _{(L,1)}$ or $\rho _{(R,0)}\ne \rho _{(R,1)}$. $\square$

In view of the considerations in Remark 3.11, we next concentrate on the case $\epsilon >0.$ The following result tells us that for $\epsilon >0$ the stationary macroscopic profiles satisfy a stationary PDE with fixed boundary conditions and also admit a stochastic representation in terms of an absorbing switching diffusion process.

Theorem 3.12

(Stationary boundary value problem) Consider the boundary value problem

$$\begin{aligned} {\left\{ \begin{array}{ll} 0 = \Delta u_0 + \Upsilon (u_1-u_0),\\ 0 = \epsilon \Delta u_1 + \Upsilon (u_0-u_1), \end{array}\right. } \end{aligned}$$

(3.44)

with boundary conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} u_0(0) = \rho _{L,0}, \ u_0(1) = \rho _{R,0},\\ u_1(0) = \rho _{L,1}, \ u_1(1) = \rho _{R,1}, \end{array}\right. } \end{aligned}$$

(3.45)

where $\epsilon ,\Upsilon >0$, and the four boundary parameters $\rho _{(L,0)},\, \rho _{(L,1)},\,\rho _{(R,0)},\,\rho _{(R,1)}$ are also positive. Then the PDE admits a unique strong solution given by

$$\begin{aligned} u_i(y) = {\rho _i^{\mathrm{{stat}}}}(y),\qquad y\in [0,1], \end{aligned}$$

(3.46)

where $({\rho _0^{\mathrm{{stat}}}}(\cdot ),{\rho _1^{\mathrm{{stat}}}}(\cdot ))$ are as defined in (3.37). Furthermore, $({\rho _0^{\mathrm{{stat}}}}(\cdot ),{\rho _1^{\mathrm{{stat}}}}(\cdot ))$ has the stochastic representation

$$\begin{aligned} {\rho _i^{\mathrm{{stat}}}}(y) = {{\mathbb {E}}}_{(y,i)}[\Phi _{i_\tau }(X_\tau )], \end{aligned}$$

(3.47)

where $\{i_t:\,t \ge 0\}$ is the pure jump process on state space $I=\{0,1\}$ that switches at rate $\Upsilon$, the functions $\Phi _0,\Phi _1:\,I\rightarrow {{\mathbb {R}}}_+$ are defined as

$$\begin{aligned} \Phi _0 = \rho _{(L,0)}\,{\varvec{1}}_{\{0\}} + \rho _{(R,0)}\,{\varvec{1}}_{\{1\}},\qquad \Phi _1 = \rho _{(L,1)}\,{\varvec{1}}_{\{0\}} + \rho _{(R,1)}\,{\varvec{1}}_{\{1\}}, \end{aligned}$$

$\{X_t:\,t \ge 0\}$ is the stochastic process [0, 1] that satisfies the SDE

$$\begin{aligned} \mathrm{d}X_t = \psi (i_t)\,\mathrm{d}W_t \end{aligned}$$

with $W_t=B_{2t}$ and $\{B_t:\, t \ge 0\}$ standard Brownian motion, the switching diffusion process $\{(X_t,i_t):\,t\ge 0\}$ is killed at the stopping time

$$\begin{aligned} \tau := \inf \{t\ge 0\,:\,X_t\in I\}, \end{aligned}$$

and $\psi :\,I\rightarrow \{1,\epsilon \}$ is given by $\psi := {\varvec{1}}_{\{0\}} + \epsilon \,{\varvec{1}}_{\{1\}}$.

Proof

It is straightforward to verify that for $\epsilon >0$ the macroscopic profiles $\rho _0,\rho _1$ defined in (3.39)−(3.40) are indeed uniformly continuous in (0, 1) and thus can be uniquely extended continuously to [0, 1], namely, by defining ${\rho _i^{\mathrm{{stat}}}}(0)=\rho _{(L,i)},\, {\rho _i^{\mathrm{{stat}}}}(1)=\rho _{(R,i)}$ for $i\in I$. Also ${\rho _i^{\mathrm{{stat}}}}\in C^\infty ([0,1])$ for $i\in I$ and satisfy the stationary PDE (3.44), with the boundary conditions specified in (3.45).

The stochastic representation of a solution of the system in (3.44) follows from [29, p385, Eq.(4.7)]. For the sake of completeness, we give the proof of uniqueness of the solution of (3.44). Let $u=(u_0,u_1)$ and $v=(v_0,v_1)$ be two solutions of the stationary reaction diffusion equation with the specified boundary conditions in (3.45). Then $(w_0,w_1) :=(u_0-v_0,u_1-v_1)$ satisfies

$$\begin{aligned} {\left\{ \begin{array}{ll} 0 = \Delta w_0 + \Upsilon (w_1-w_0),\\ 0 = \epsilon \Delta w_1 + \Upsilon (w_0-w_1), \end{array}\right. } \end{aligned}$$

(3.48)

with boundary conditions

$$\begin{aligned} w_0(0) = w_0(1) = w_1(0) = w_1(1) = 0. \end{aligned}$$

(3.49)

Multiplying the two equations in (3.48) with $w_0$ and $w_1$, respectively, and using the identity

$$\begin{aligned} w_i\Delta w_i = \nabla \cdot (w_i\nabla w_i)-|\nabla w_i|^2,\quad i\in I, \end{aligned}$$

we get

$$\begin{aligned} {\left\{ \begin{array}{ll} 0 = \nabla \cdot (w_0\nabla w_0)-|\nabla w_0|^2+\Upsilon (w_1-w_0)w_0,\\ 0 = \epsilon \nabla \cdot (w_1\nabla w_1)-\epsilon |\nabla w_1|^2+\Upsilon (w_0-w_1)w_1. \end{array}\right. } \end{aligned}$$

(3.50)

Integrating both equations by parts over [0, 1],  we get

$$\begin{aligned} \begin{aligned} 0&= -[w_0(1)\nabla w_0(1)-w_0(0)\nabla w_0(0)] - \int _{0}^{1} dy\,|\nabla w_0(y)|^2 \\&\quad +\Upsilon \int _{0}^{1}dy\,(w_1(y)-w_0(y))w_0(y),\\ 0&=-\epsilon [w_1(1)\nabla w_1(1)-w_1(0)\nabla w_1(0)] - \epsilon \int _{0}^{1} dy\,|\nabla w_1(y)|^2 \\&\quad +\Upsilon \int _{0}^{1}dy\,(w_0(y)-w_1(y))w_1(y). \end{aligned} \end{aligned}$$

(3.51)

Adding the above two equations and using the zero boundary conditions in (3.49), we have

$$\begin{aligned} \int _{0}^{1} dy\,|\nabla w_0(y)|^2+\epsilon \int _{0}^{1} dy\,|\nabla w_1(y)|^2+\Upsilon \int _{0}^{1}dy\,[w_1(y)-w_0(y)]^2 = 0. \end{aligned}$$

(3.52)

Since both $w_0$ and $w_1$ are continuous and $\epsilon>0,\Upsilon >0$, it follows that

$$\begin{aligned} w_0 = w_1,\quad \nabla w_0 = \nabla w_1 = 0, \end{aligned}$$

(3.53)

and so $w_0=w_1\equiv 0$. $\square$

Note that, as a result of Theorem 3.12, the four absorption probabilities of the switching diffusion process $\{(X_t,i_t)\,:\,t\ge 0\}$ starting from $(y,i)\in [0,1]\times I$ are indeed the respective coefficients of $\rho _{(L,0)},\rho _{(L,1)},\rho _{(R,0)}$, $\rho _{(R,1)}$ appearing in the expression of ${\rho _i^{\mathrm{{stat}}}}(y)$. Furthermore note that, as a consequence of Theorem 3.12 and the results in [33, Section 3], the time-dependent boundary-value problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t \rho _0 = \Delta \rho _0 + \Upsilon (\rho _1-\rho _0),\\ \partial _t \rho _1 = \epsilon \Delta \rho _1 + \Upsilon (\rho _0-\rho _1), \end{array}\right. } \end{aligned}$$

(3.54)

with initial conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} \rho _0(x,0) = {\bar{\rho }}_0(x),\\ \rho _1(x,0) = {\bar{\rho }}_1(x), \end{array}\right. } \end{aligned}$$

(3.55)

and boundary conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} \rho _0(0,t) = \rho _{L,0}, \ \rho _0(1,t) = \rho _{R,0},\\ \rho _1(0,t) = \rho _{L,1}, \ \rho _1(1,t) = \rho _{R,1}, \end{array}\right. } \end{aligned}$$

(3.56)

admits a unique solution given by

$$\begin{aligned} {\left\{ \begin{array}{ll} \rho _0(x,t) = \rho ^{\text {hom}}_0(x,t)+ {\rho _0^{\mathrm{{stat}}}}(x),\\ \rho _1(x,t) = \rho ^{\text {hom}}_1(x,t)+ {\rho _1^{\mathrm{{stat}}}}(x), \end{array}\right. } \end{aligned}$$

(3.57)

where

$$\begin{aligned} \rho _0^{\text {hom}}(x,t)= & {} \mathrm{e}^{-\Upsilon t}h_0(x,t)+\frac{\Upsilon }{1-\epsilon } \mathrm{e}^{-\Upsilon t}\int _{\epsilon t}^t \mathrm{d}s\,\left( \left( \frac{s-\epsilon t}{t-s}\right) ^{1/2}I_1(\upsilon (s))h_0(x,s) \right. \nonumber \\&\quad \left. +I_0(\upsilon (s))h_1(x,s) \right) , \end{aligned}$$

(3.58)

$$\begin{aligned} \rho _1^{\text {hom}}(x,t)= & {} \mathrm{e}^{-\Upsilon t}h_1(x,\epsilon t)+\frac{\Upsilon }{1-\epsilon }\mathrm{e}^{-\Upsilon t}\int _{\epsilon t}^t \mathrm{d}s\, \left( \left( \frac{s-\epsilon t}{t-s}\right) ^{-1/2}I_1(\upsilon (s))h_1(x,s) \right. \nonumber \\&\quad \left. +I_0(\upsilon (s))h_0(x,s) \right) , \end{aligned}$$

(3.59)

$\upsilon (s)=\frac{2\Upsilon }{1-\epsilon }((t-s)(s-\epsilon t))^{1/2}$, $I_0(\cdot )$ and $I_1(\cdot )$ are the modified Bessel functions, $h_0(x,t)$, $h_1(x,t)$ are the solutions of

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t h_0 = \Delta h_0, \\ \partial _t h_1 = \Delta h_1, \\ h_0(x,0)= {\bar{\rho }}_0(x)-{\rho _0^{\mathrm{{stat}}}}(x), \\ h_1(x,1)= {\bar{\rho }}_1(x) -{\rho _1^{\mathrm{{stat}}}}(x),\\ h_0(0,t)= h_0(1,t)= h_1(0,t)=h_1(1,t)=0, \end{array}\right. } \end{aligned}$$

(3.60)

and ${\rho _0^{\mathrm{{stat}}}}(x)$, ${\rho _1^{\mathrm{{stat}}}}(x)$ are given in (3.40).

We conclude this section by proving that the solution of the time-dependent boundary-value problem in (3.54) converges to the stationary profile in (3.40).

Proposition 3.13

(Convergence to stationary profile) Let ${\rho _0^{\mathrm{{hom}}}}(x,t)$ and ${\rho _1^{\mathrm{{hom}}}}(x,t)$ be as in (3.58) and (3.59), respectively, i.e., the solutions of the boundary-value problem (3.54) with zero boundary conditions and initial conditions given by ${\rho _0^{\mathrm{{hom}}}}(x,0)= {\bar{\rho }}_0(x)-{\rho _0^{\mathrm{{stat}}}}(x)$ and ${\rho _1^{\mathrm{{hom}}}}(x,0)= {\bar{\rho }}_1(x) -{\rho _1^{\mathrm{{stat}}}}(x)$. Then, for any $k\in {{\mathbb {N}}}$,

$$\begin{aligned} \lim _{t\rightarrow \infty } \Big [\Vert {\rho _0^{\mathrm{{hom}}}}(x,t)\Vert _{C^k(0,1)}+\Vert {\rho _1^{\mathrm{{hom}}}}(x,t)\Vert _{C^k(0,1)}\Big ]=0. \end{aligned}$$

Proof

We start by showing that

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }\,\Big [ \Vert {\rho _0^{\mathrm{{hom}}}}(x,t)\Vert _{L^2(0,1)}+\Vert {\rho _1^{\mathrm{{hom}}}}(x,t)\Vert _{L^2(0,1)}\Big ]=0. \end{aligned}$$

(3.61)

Multiply the first equation of (3.54) by $\rho _0$ and the second equation by $\rho _1$. Integration by parts yields

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t\left( \int _0^1 \mathrm{d}x\,\rho _0^2 \right) =-\int _0^1 \mathrm{d}x\,|\partial _x \rho _0|^2 +\Upsilon \int _0^1 \mathrm{d}x\,(\rho _1\rho _0-\rho _0^2),\\ \partial _t\left( \int _0^1 \mathrm{d}x\,\rho _1^2(x,t) \right) =-\epsilon \int _0^1 \mathrm{d}x\,|\partial _x \rho _1|^2 +\Upsilon \int _0^1 \mathrm{d}x\,(\rho _0\rho _1-\rho _1^2). \end{array}\right. } \end{aligned}$$

(3.62)

Summing the two equations and defining $E(t):= \int _0^1 \mathrm{d}x\,(\rho _0(x,t)^2 +\rho _1(x,t)^2)$, we obtain

$$\begin{aligned} \partial _tE(t)=-\left( \int _0^1 \mathrm{d}x\,|\partial _x \rho _0|^2 + \epsilon \int _0^1 \mathrm{d}x\,|\partial _x \rho _1|^2 \right) -\Upsilon \int _0^1 \mathrm{d}x\,(\rho _0-\rho _1)^2. \end{aligned}$$

(3.63)

By the Poincaré inequality (i.e., $\int _0^1 \mathrm{d}x\,|\partial _x \rho _i(x,t)|^2 \ge C_p \int _0^1 \mathrm{d}x\ |\rho _i(x,t)|^2$, with $C_p>0$) we have $\partial _tE(t)\le -\epsilon C_p E(t)$, from which we obtain

$$\begin{aligned} E(t)\le \mathrm{e}^{-C_pt}E(0), \end{aligned}$$

and hence (3.61).

From [45, Theorem 2.1] it follows that

$$\begin{aligned} A:=\left[ \begin{array}{c c c c} \Delta -\Upsilon &{} \Upsilon \\ \Upsilon &{} \epsilon \Delta -\Upsilon \\ \end{array} \right] , \end{aligned}$$

with domain $D(A)=H^2(0,1)\cap H_0^1(0,1)$, generates a semigroup $\{{\mathcal {S}}_t:\, t\ge 0\}$. If we set $\vec {\rho }(t)={\mathcal {S}}_t (\vec {\bar{\rho }}^{\text {hom}})$, with $\vec {\bar{\rho }}^{\text {hom}}=\vec {\bar{\rho }}-\vec {\rho }^{\text {stat}}$, then by the semigroup property we have

$$\begin{aligned} \vec {\rho }(t)={\mathcal {S}}_{t-1}({\mathcal {S}}_{1/k})^k(\vec {\bar{\rho }}^{{\text {hom}}}), \qquad t \ge 1, \end{aligned}$$

and hence $A^k\vec {\rho }(t)={\mathcal {S}}_{t-1}(A{\mathcal {S}}_{1/k})^k(\vec {\bar{\rho }}^{\text {hom}})$. If we set $\vec {p}:=(A{\mathcal {S}}_{1/k})^k(\vec {\bar{\rho }}^{\text {hom}})$, then we obtain, by [45, Theorem 5.2(d)],

$$\begin{aligned} \Vert A^k \vec {\rho }(t) \Vert _{L^2(0,1)}\le \Vert {\mathcal {S}}_{t-1}\vec {p}\Vert _{L^2(0,1)}, \end{aligned}$$

where $\lim _{t\rightarrow \infty }\Vert {\mathcal {S}}_{t-1}\vec {p}\Vert _{L^2(0,1)}=0$ by the first part of the proof. The compact embedding

$$\begin{aligned} D(A^k)\hookrightarrow H^{2k}(0,1)\hookrightarrow C^k(0,1), \qquad k\in {{\mathbb {N}}}, \end{aligned}$$

concludes the proof. $\square$

3.4 The Stationary Current

In this section we compute the expected current in the non-equilibrium steady state that is induced by different densities at the boundaries. We consider the microscopic and macroscopic systems, respectively.

Microscopic system

We start by defining the notion of current. The microscopic currents are associated with the edges of the underlying two-layer graph. In our setting, we denote by ${{{\mathcal {J}}}}^0_{x,x+1}(t)$ and ${{{\mathcal {J}}}}^1_{x,x+1}(t)$ the instantaneous current through the horizontal edge $(x,x+1)$, $x\in V$, of the bottom layer, respectively, top layer at time t. Obviously,

$$\begin{aligned} {{{\mathcal {J}}}}^0_{x,x+1}(t) = \eta _{0}(x,t) - \eta _{0}(x+1,t), \qquad \qquad {{{\mathcal {J}}}}^1_{x,x+1}(t) = \epsilon [\eta _{1}(x,t) - \eta _{1}(x+1,t)]. \end{aligned}$$

We are interested in the stationary currents ${J}^0_{x,x+1}$, respectively, ${J}^1_{x,x+1}$, which are obtained as

$$\begin{aligned} J^0_{x,x+1} = {{\mathbb {E}}}_{stat}[\eta _{0}(x) - \eta _{0}(x+1)], \qquad \qquad J^1_{x,x+1} = \epsilon {{\mathbb {E}}}_{stat}[\eta _{1}(x) - \eta _{1}(x+1)], \end{aligned}$$

(3.64)

where ${{\mathbb {E}}}_{stat}$ denotes expectation w.r.t. the unique invariant probability measure of the microscopic system $\{\eta (t):\, t \ge 0\}$ with $\eta (t) = \{\eta _{0}(x,t),\eta _{1}(x,t)\}_{x\in V}$. In other words, $J^0_{x,x+1}$ and $J^1_{x,x+1}$ give the average flux of particles of type 0 and type 1 across the bond $(x,x+1)$ due to diffusion.

Of course, the average number of particle at each site varies in time also as a consequence of the reaction term:

$$\begin{aligned} \frac{d}{dt} {{\mathbb {E}}}[\eta _0(x,t)]= & {} {{\mathbb {E}}}[{{{\mathcal {J}}}}^0_{x-1,x}(t) - {{{\mathcal {J}}}}^0_{x,x+1}(t)] +\gamma ( {{\mathbb {E}}}[\eta _1(x,t)] - {{\mathbb {E}}}[\eta _0(x,t)]), \\ \frac{d}{dt} {{\mathbb {E}}}[\eta _1(x,t)]= & {} {{\mathbb {E}}}[{{{\mathcal {J}}}}^1_{x-1,x}(t) - {{{\mathcal {J}}}}^1_{x,x+1}(t)] + \gamma ({{\mathbb {E}}}[\eta _0(x,t)] - {{\mathbb {E}}}[\eta _1(x,t)]). \end{aligned}$$

Summing these equations, we see that there is no contribution of the reaction part to the variation of the average number of particles at site x:

$$\begin{aligned} \frac{d}{dt} {{\mathbb {E}}}[\eta _0(x,t) + \eta _1(x,t)] = {{\mathbb {E}}}[{{{\mathcal {J}}}}_{x-1,x}(t) - {{{\mathcal {J}}}}_{x,x+1}(t)]. \end{aligned}$$

The sum

$$\begin{aligned} J_{x,x+1} = J^0_{x,x+1} + J^1_{x,x+1}, \end{aligned}$$

(3.65)

with $J^0_{x,x+1}$ and $J^1_{x,x+1}$ defined in (3.64), will be called the stationary current between sites at $x,x+1$, $x\in V$, which is responsible for the variation of the total average number of particles at each site, regardless of their type.

Proposition 3.14

(Stationary microscopic current) For $x \in \{2,\ldots ,N-1\}$ the stationary currents defined in (3.64) are given by

$$\begin{aligned} J^0_{x,x+1} = - \tfrac{1+\gamma }{1+N+2N\gamma }[\rho _{(R,0)}-\rho _{(L,0)}]-\tfrac{\gamma }{1+N+2N\gamma }[\rho _{(R,1)}-\rho _{(L,1)}],\quad J^1_{x,x+1} = 0, \end{aligned}$$

(3.66)

when $\epsilon =0$ and by

$$\begin{aligned} \begin{aligned} J^0_{x,x+1}&= - \vec {c}_1\cdot \vec {\rho } - \epsilon [(\vec {c}_3\cdot \vec {\rho }) \alpha _1^x (\alpha _1 - 1) + (\vec {c}_4\cdot \vec {\rho }) \alpha _2^x (\alpha _2 - 1)],\\ J^1_{x,x+1}&= - \epsilon \vec {c}_1\cdot \vec {\rho } + \epsilon [(\vec {c}_3\cdot \vec {\rho }) \alpha _1^x (\alpha _1 - 1) + (\vec {c}_4\cdot \vec {\rho }) \alpha _2^x (\alpha _2 - 1)], \end{aligned} \end{aligned}$$

(3.67)

when $\epsilon >0,$ where $\vec {c}_1, \vec {c}_3, \vec {c}_4$ are the vectors defined in (A.4) of Appendix A, and $\alpha _1,\alpha _2$ are defined in (3.31). As a consequence, the current $J_{x,x+1}= J^0_{x,x+1} + J^1_{x,x+1}$ is independent of x and is given by

$$\begin{aligned} J_{x,x+1} = - \tfrac{1+\gamma }{1+N+2N\gamma }[\rho _{(R,0)}-\rho _{(L,0)}]-\tfrac{\gamma }{1+N+2N\gamma }[\rho _{(R,1)}-\rho _{(L,1)}] \end{aligned}$$

(3.68)

when $\epsilon = 0$ and

$$\begin{aligned} J_{x,x+1} = - (1+\epsilon )\left[ C_1\,(\rho _{R,0}-\rho _{L,0})+\epsilon \,C_2\,(\rho _{R,1}-\rho _{L,1})\right] \end{aligned}$$

(3.69)

when $\epsilon >0$, where

$$\begin{aligned} \begin{aligned} C_1&= \frac{[\alpha _1(1-\epsilon )(\alpha _1^{N-1}-1) + \epsilon \,(\alpha _1^{N+1}-1)]}{\alpha _1(1-\epsilon )(\alpha _1^{N-1}-1)(N+1)+2\epsilon \,(\alpha _1^{N+1}-1)(N+\epsilon )},\\ C_2&= \frac{(\alpha _1^{N+1}-1)}{\alpha _1(1-\epsilon )(\alpha _1^{N-1}-1)(N+1) +2\epsilon \,(\alpha _1^{N+1}-1)(N+\epsilon )}. \end{aligned} \end{aligned}$$

(3.70)

Proof

From (3.64) we have

$$\begin{aligned} J^0_{x,x+1} = \theta _0(x) - \theta _0(x+1), \qquad \qquad J^1_{x,x+1} = \epsilon [\theta _1(x) - \theta _1(x+1)], \end{aligned}$$

(3.71)

where $\theta _0(\cdot ),\theta _1(\cdot )$ are the average microscopic profiles. Thus, when $\epsilon =0$, the expressions of $J^0_{x,x+1},J^1_{x,x+1}$ and consequently $J_{x,x+1}$ follow directly from (3.21).

For $\epsilon >0$, using the expressions of $\theta _0(\cdot ),\theta _1(\cdot )$ in (3.33), we see that

$$\begin{aligned} \begin{aligned} J^0_{x,x+1}&= \theta _0(x)-\theta _0(x+1)= - \vec {c}_1\cdot \vec {\rho } - \epsilon [(\vec {c}_3\cdot \vec {\rho }) \alpha _1^x (\alpha _1 - 1) + (\vec {c}_4\cdot \vec {\rho }) \alpha _2^x (\alpha _2 - 1)],\\ J^1_{x,x+1}&=\epsilon [\theta _1(x)-\theta _1(x+1)]= - \epsilon \vec {c}_1\cdot \vec {\rho } + \epsilon [(\vec {c}_3\cdot \vec {\rho }) \alpha _1^x (\alpha _1 - 1) + (\vec {c}_4\cdot \vec {\rho }) \alpha _2^x (\alpha _2 - 1)], \end{aligned} \end{aligned}$$

(3.72)

where $\vec {c}_1, \vec {c}_3, \vec {c}_4$ are the vectors defined in (A.4) of Appendix A, and $\alpha _1,\alpha _2$ are defined in (3.31). Adding the two equations, we also have

$$\begin{aligned} J_{x,x+1} = J^0_{x,x+1} + J^1_{x,x+1} = -(1+\epsilon )\,\vec {c}_1\cdot \vec {\rho }= (1+\epsilon )\left[ C_1\,(\rho _{R,0}-\rho _{L,0})+\epsilon \,C_2\,(\rho _{R,1}-\rho _{L,1})\right] , \end{aligned}$$

(3.73)

where $C_1,C_2$ are as in (3.70). $\square$

Macroscopic system

The microscopic current scales like 1/N. Indeed, the currents associated to the two layers in the macroscopic system can be obtained from the microscopic currents, respectively, by defining

$$\begin{aligned} J^0(y) = \lim _{N\rightarrow \infty } N J^0_{\lfloor yN\rfloor ,\lfloor yN\rfloor +1}, \qquad J^1(y) = \lim _{N\rightarrow \infty } N J^1_{\lfloor yN\rfloor ,\lfloor yN\rfloor +1}. \end{aligned}$$

(3.74)

Below we justify the existence of the two limits and thereby provide explicit expressions for the macroscopic currents.

Proposition 3.15

(Stationary macroscopic current) For $y \in (0,1)$ the stationary currents defined in (3.74) are given by

$$\begin{aligned} J^0(y) = -\left[ (\rho _{R,0}-\rho _{L,0})\right] ,\quad J^1(y) = 0, \end{aligned}$$

(3.75)

when $\epsilon =0$ and by

$$\begin{aligned} \begin{aligned} J^0(y)&=\frac{\epsilon B_{\epsilon ,\Upsilon }}{1+\epsilon }\left[ \frac{\cosh \left[ B_{\epsilon ,\Upsilon }\,(1-y)\right] }{\sinh \left[ B_{\epsilon ,\Upsilon }\right] }\,(\rho _{(L,0)}-\rho _{(L,1)}) -\frac{\cosh \left[ B_{\epsilon ,\Upsilon }\,y\right] }{\sinh \left[ B_{\epsilon ,\Upsilon }\right] }\,(\rho _{(R,0)}-\rho _{(R,1)})\right] \\&\quad -\frac{1}{1+\epsilon }\left[ (\rho _{(R,0)}-\rho _{(L,0)})+\epsilon (\rho _{(R,1)}-\rho _{(L,1)})\right] \end{aligned} \end{aligned}$$

(3.76)

and

$$\begin{aligned} \begin{aligned} J^1(y)&=-\frac{\epsilon B_{\epsilon ,\Upsilon }}{1+\epsilon }\left[ \frac{\cosh \left[ B_{\epsilon ,\Upsilon }\,(1-y)\right] }{\sinh \left[ B_{\epsilon ,\Upsilon }\right] }\,(\rho _{(L,0)}-\rho _{(L,1)}) -\frac{\cosh \left[ B_{\epsilon ,\Upsilon }\,y\right] }{\sinh \left[ B_{\epsilon ,\Upsilon }\right] }\,(\rho _{(R,0)}-\rho _{(R,1)})\right] \\&\quad -\frac{\epsilon }{1+\epsilon }\left[ (\rho _{(R,0)}-\rho _{(L,0)})+\epsilon (\rho _{(R,1)}-\rho _{(L,1)})\right] \end{aligned} \end{aligned}$$

(3.77)

when $\epsilon > 0$. As a consequence, the total current $J(y)= J^0(y) + J^1(y)$ is constant and is given by

$$\begin{aligned} J(y) = -\left[ (\rho _{R,0}-\rho _{L,0})+\epsilon \,(\rho _{R,1}-\rho _{L,1})\right] . \end{aligned}$$

(3.78)

Proof

For $\epsilon =0$ the claim easily follows from the expressions of $J^0_{x,x+1}, J^1_{x,x+1}$ given in (3.66) and the fact that $\gamma _N\rightarrow 0$ as $N\rightarrow \infty$.

When $\epsilon >0$, we first note the following:

$$\begin{aligned} \begin{aligned}&\gamma _N N^2\overset{N\rightarrow \infty }{\longrightarrow } \Upsilon >0,\\&\quad \lim \limits _{N\rightarrow \infty }\alpha _1= \lim \limits _{N\rightarrow \infty }\alpha _2=1,\\&\quad \lim \limits _{N\rightarrow \infty }N(\alpha _1-1)=-B_{\epsilon ,\Upsilon },\ \lim \limits _{N\rightarrow \infty }N(\alpha _2-1)=B_{\epsilon ,\Upsilon },\\&\quad \lim \limits _{N\rightarrow \infty }\alpha _1^N = \mathrm{e}^{-B_{\epsilon ,\Upsilon }},\quad \lim \limits _{N\rightarrow \infty }\alpha _2^N = \mathrm{e}^{B_{\epsilon ,\Upsilon }}. \end{aligned} \end{aligned}$$

(3.79)

Consequently, from the expressions for $(\vec {c}_i)_{1\le i \le 4}$ defined in (A.4), we also have

$$\begin{aligned} \begin{aligned} \lim \limits _{N\rightarrow \infty }N\vec {c}_1&= \frac{1}{1+\epsilon }\,\big [ \begin{array}{c c c c} -1&-\epsilon&1&\epsilon \end{array} \big ]^T,\\ \lim \limits _{N\rightarrow \infty }\vec {c}_3&= \frac{1}{1+\epsilon }\,\big [ \begin{array}{c c c c} \frac{\mathrm{e}^{B_{\epsilon ,\Upsilon }}}{\mathrm{e}^{B_{\epsilon ,\Upsilon }}-\mathrm{e}^{-B_{\epsilon ,\Upsilon }}}&-\frac{\mathrm{e}^{B_{\epsilon ,\Upsilon }}}{\mathrm{e}^{B_{\epsilon ,\Upsilon }}-\mathrm{e}^{-B_{\epsilon ,\Upsilon }}}&-\frac{1}{\mathrm{e}^{B_{\epsilon ,\Upsilon }}-\mathrm{e}^{-B_{\epsilon ,\Upsilon }}}&\frac{1}{\mathrm{e}^{B_{\epsilon ,\Upsilon }}-\mathrm{e}^{-B_{\epsilon ,\Upsilon }}} \end{array} \big ]^T,\\ \lim \limits _{N\rightarrow \infty }\vec {c}_4&= \frac{1}{1+\epsilon }\,\big [ \begin{array}{c c c c} -\frac{\mathrm{e}^{-B_{\epsilon ,\Upsilon }}}{\mathrm{e}^{B_{\epsilon ,\Upsilon }}-\mathrm{e}^{-B_{\epsilon ,\Upsilon }}}&\frac{\mathrm{e}^{-B_{\epsilon ,\Upsilon }}}{\mathrm{e}^{B_{\epsilon ,\Upsilon }}-\mathrm{e}^{-B_{\epsilon ,\Upsilon }}}&\frac{1}{\mathrm{e}^{B_{\epsilon ,\Upsilon }}-\mathrm{e}^{-B_{\epsilon ,\Upsilon }}}&-\frac{1}{\mathrm{e}^{B_{\epsilon ,\Upsilon }}-\mathrm{e}^{-B_{\epsilon ,\Upsilon }}} \end{array} \big ]^T. \end{aligned} \end{aligned}$$

(3.80)

Combining the above equations with (3.67), we have

$$\begin{aligned} \begin{aligned} J^0(y)&= \lim _{N\rightarrow \infty } N J^0_{\lfloor yN\rfloor ,\lfloor yN\rfloor +1}\\&= -\epsilon B_{\epsilon ,\Upsilon }\Big [\Big (\lim \limits _{N\rightarrow \infty }\vec {c}_4\cdot \vec {\rho }\Big )\,\mathrm{e}^{B_{\epsilon ,\Upsilon }y}-\Big (\lim \limits _{N\rightarrow \infty }\vec {c}_3\cdot \vec {\rho }\Big )\,\mathrm{e}^{-B_{\epsilon ,\Upsilon }y}\Big ]-\Big (\lim \limits _{N\rightarrow \infty }N\vec {c}_1\cdot \vec {\rho }\Big )\\&=\frac{\epsilon B_{\epsilon ,\Upsilon }}{1+\epsilon }\left[ \frac{\cosh \left[ B_{\epsilon ,\Upsilon }\,(1-y)\right] }{\sinh \left[ B_{\epsilon ,\Upsilon }\right] }\,(\rho _{(L,0)}-\rho _{(L,1)}) -\frac{\cosh \left[ B_{\epsilon ,\Upsilon }\,y\right] }{\sinh \left[ B_{\epsilon ,\Upsilon }\right] }\,(\rho _{(R,0)}-\rho _{(R,1)})\right] \\&\quad -\frac{1}{1+\epsilon }\left[ (\rho _{(R,0)}-\rho _{(L,0)})+\epsilon (\rho _{(R,1)}-\rho _{(L,1)})\right] \end{aligned} \end{aligned}$$

(3.81)

and, similarly,

$$\begin{aligned} \begin{aligned} J^1(y)&= \lim _{N\rightarrow \infty } N J^1_{\lfloor yN\rfloor ,\lfloor yN\rfloor +1}\\&= \epsilon B_{\epsilon ,\Upsilon }\Big [\Big (\lim \limits _{N\rightarrow \infty }\vec {c}_4\cdot \vec {\rho }\Big )\,\mathrm{e}^{B_{\epsilon ,\Upsilon }y}-\Big (\lim \limits _{N\rightarrow \infty }\vec {c}_3\cdot \vec {\rho }\Big )\,\mathrm{e}^{-B_{\epsilon ,\Upsilon }y}\Big ]-\epsilon \,\Big (\lim \limits _{N\rightarrow \infty }N\vec {c}_1\cdot \vec {\rho }\Big )\\&=-\frac{\epsilon B_{\epsilon ,\Upsilon }}{1+\epsilon }\left[ \frac{\cosh \left[ B_{\epsilon ,\Upsilon }\,(1-y)\right] }{\sinh \left[ B_{\epsilon ,\Upsilon }\right] }\,(\rho _{(L,0)}-\rho _{(L,1)}) -\frac{\cosh \left[ B_{\epsilon ,\Upsilon }\,y\right] }{\sinh \left[ B_{\epsilon ,\Upsilon }\right] }\,(\rho _{(R,0)}-\rho _{(R,1)})\right] \\&\quad -\frac{\epsilon }{1+\epsilon }\left[ (\rho _{(R,0)}-\rho _{(L,0)})+\epsilon (\rho _{(R,1)}-\rho _{(L,1)})\right] . \end{aligned} \end{aligned}$$

(3.82)

Adding $J^0(y)$ and $J^1(y)$, we obtain the total current

$$\begin{aligned} J(y)=J^0(y)+J^1(y)=-\left[ (\rho _{R,0}-\rho _{L,0})+\epsilon \,(\rho _{R,1}-\rho _{L,1})\right] , \end{aligned}$$

(3.83)

which is indeed independent of y. $\square$

Remark 3.16

(Currents) Combining the expressions for the density profiles and the current, we see that

$$\begin{aligned} J^0(y) = - \frac{d\rho _0}{dy} (y), \qquad J^1(y) = - \epsilon \frac{d\rho _1}{dy} (y). \end{aligned}$$

$\square$

3.5 Discussion: Fick’s Law and Uphill Diffusion

In this section we discuss the behaviour of the boundary-driven system as the parameter $\epsilon$ is varied. For simplicity we restrict our discussion to the macroscopic setting, although similar comments hold for the microscopic system as well.

In view of the previous results, we can rewrite the equations for the densities $\rho _0(y,t),\rho _1(y,t)$ as

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t \rho _0 = -\nabla J^0 + \Upsilon (\rho _1-\rho _0),\\ \partial _t \rho _1 = -\nabla J^1 + \Upsilon (\rho _0-\rho _1),\\ J_0 = - \nabla \rho _0, \\ J_1 = -\epsilon \nabla \rho _1, \end{array}\right. } \end{aligned}$$

which are complemented with the boundary values (for $\epsilon >0$)

$$\begin{aligned} {\left\{ \begin{array}{ll} \rho _0(0,t) = \rho _{L,0}, \ \rho _0(1,t) = \rho _{R,0},\\ \rho _1(0,t) = \rho _{L,1}, \ \rho _1(1,t) = \rho _{R,1}. \end{array}\right. } \end{aligned}$$

We will be concerned with the total density $\rho = \rho _0 +\rho _1$, whose evolution equation does not contain the reaction part, and is given by

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t \rho = - \nabla J,\\ J = - \nabla ( \rho _0 + \epsilon \rho _1), \end{array}\right. } \end{aligned}$$

(3.84)

with boundary values

$$\begin{aligned} {\left\{ \begin{array}{ll} \rho (0,t) = \rho _L = \rho _{L,0}+ \rho _{R,0},\\ \rho (1,t) = \rho _R = \rho _{R,0}+\rho _{R,1}. \end{array}\right. } \end{aligned}$$

(3.85)

Non-validity of Fick’s law From (3.84) we immediately see that Fick’s law of mass transport is satisfied if and only if $\epsilon =1$. When we allow diffusion and reaction of slow and fast particles, i.e., $0 \le \epsilon <1$, Fick’s law breaks down, since the current associated to the total mass is not proportional to the gradient of the total mass. Rather, the current J is the sum of a contribution $J^0$ due to the diffusion of fast particles of type 0 (at rate 1) and a contribution $J^1$ due to the diffusion of slow particles of type 1 (at rate $\epsilon$). Interestingly, the violation of Fick’s law opens up the possibility of several interesting phenomena that we discuss in what follows.

Equal boundary densities with non-zero current In a system with diffusion and reaction of slow and fast particles we may observe a non-zero current when the total density has the same value at the two boundaries. This is different from what is observed in standard diffusive systems driven by boundary reservoirs, where in order to have a stationary current it is necessary that the reservoirs have different chemical potentials, and therefore different densities, at the boundaries.

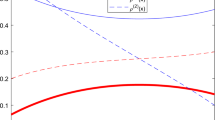
Let us, for instance, consider the specific case when $\rho _{L,0} =\rho _{R,1} = 2$ and $\rho _{L,1} = \rho _{R,0} = 4$, which indeed implies equal densities at the boundaries given by $\rho _{L} =\rho _{R} = 6$. The density profiles and currents are displayed in Fig. 3 for two values of $\epsilon$, which shows the comparison between the Fick-regime $\epsilon = 1$ (left panels) and the non-Fick-regime with very slow particles $\epsilon = 0.001$ (right panels).

On the one hand, in the Fick-regime the profile of both types of particles interpolates between the boundary values, with a slightly non-linear shape that has been quantified precisely in (3.39)–(3.40). Furthermore, in the same regime $\epsilon =1$, the total density profile is flat and the total current J vanishes because $J^0(y) = -J^1(y)$ for all $y\in [0,1]$.

On the other hand, in the non-Fick-regime with $\epsilon = 0.001$, the stationary macroscopic profile for the fast particles interpolates between the boundary values almost linearly (see (3.43)), whereas the profile for the slow particles is non-monotone: it has two bumps at the boundaries and in the bulk closely follows the other profile. This non-monotonicity in the profile of the slow particles is due to the non-uniform convergence in the limit $\epsilon \downarrow 0$, as pointed out in the last part of Remark 3.11. As a consequence, the total density profile is not flat and has two bumps at the boundaries. Most strikingly, the total current is $J=-2$, since now the current of the bottom layer $J^0$ is dominating, while the current of the bottom layer $J^1$ is small (order $\epsilon$).

Fig. 3

Macroscopic profiles of the densities for slow and fast particles (top panels), macroscopic profile of the total density (central panels), and the currents (bottom panels). Here, $\rho _{(L,0)}=2,\,\rho _{(L,1)}=4,\,\rho _{(R,0)}=4$ and $\rho _{(R,1)}=2, \Upsilon =1$. For the panels in the left column, $\epsilon =1$ and for the panels in the right column, $\epsilon =0.001$

Unequal boundary densities with uphill diffusion As argued earlier, since the system does not always obey Fick’s law, by tuning the parameters $\rho _{(L,0)}$, $\rho _{(L,1)}$, $\rho _{(R,0)}$, $\rho _{(R,1)}$ and $\epsilon$, we can push the system into a regime where the total current is such that $J<0$ and the total densities are such that $\rho _R < \rho _L$, where $\rho _R = \rho _{(R,0)}+\rho _{(R,1)}$ and $\rho _L = \rho _{(L,0)}+\rho _{(L,1)}$. In this regime, the current goes uphill, since the total density of particles at the right is lower than at the left, yet the average current is negative.

Fig. 4

Macroscopic profiles of the densities for slow and fast particles (top panels), macroscopic profile of the total density (central panels), and the currents (bottom panels). Here, $\rho _{(L,0)}=2,\,\rho _{(L,1)}=6,\,\rho _{(R,0)}=4$ and $\rho _{(R,1)}=2, \Upsilon =1$. For the panels in the left column, $\epsilon =1$ and for the panels in the right column, $\epsilon =0.001$

Fig. 5

Macroscopic profiles of the densities for slow and fast particles (top panels), macroscopic profile of the total density (central panels), and the currents (bottom panels) in the “mild" downhill and the “mild" uphill regime. Here, $\rho _{(L,0)}=2,\,\rho _{(L,1)}=6,\,\rho _{(R,0)}=4$ and $\rho _{(R,1)}=2, \Upsilon =1$. For the panels in the left column, $\epsilon =0.75$ and for the panels in the right column, $\epsilon =0.25$

For an illustration, consider the case when $\rho _{L,1} =6, \rho _{R,0}=4$ and $\rho _{L,0} =\rho _{R,1} = 2$, which implies $\rho _{L} = 8$ and $\rho _{R} = 6$ and thus $\rho _{R} < \rho _{L}$. The density profiles and currents are shown in Fig. 4 for two values of $\epsilon$, in particular, a comparison between the Fick-regime $\epsilon = 1$ (left panels) and the non-Fick-regime with very slow particles $\epsilon = 0.001$ (right panels). As can be seen in the figure, when $\epsilon =1,$ the system obeys Fick’s law: the total density linearly interpolates between the two total boundary densities 8 and 6, respectively. The average total stationary current is positive as predicted by Fick’s law. However, in the uphill regime, the total density is non-linear and the gradient of the total density is not proportional to the total current, violating Fick’s law. The total current is negative and is effectively dominated by the current of the fast particles. It will be shown later that the transition into the uphill regime happens at the critical value $\epsilon = \tfrac{|\rho _{(R,0)}-\rho _{(L,0)}|}{|\rho _{(R,1)}-\rho _{(L,1)}|} = \tfrac{1}{2}$. In the limit $\epsilon \downarrow 0$ the total density profile and the current always get dominated in the bulk by the profile and the current of the fast particles, respectively. When $\epsilon <\tfrac{1}{2}$, even though the density of the slow particles makes the total density near the boundaries such that $\rho _R < \rho _L$, it is not strong enough to help the system overcome the domination of the fast particles in the bulk, and so the effective total current goes in the same direction as the current of the fast particles, producing an uphill current.

The transition between downhill and uphill We observe that for the choice of reservoir parameters $\rho _{L,1} =6, \rho _{R,0}=4$ and $\rho _{L,0} =\rho _{R,1} = 2$, the change from downhill to uphill diffusion occurs at $\epsilon = \tfrac{|\rho _{(R,0)}-\rho _{(L,0)}|}{|\rho _{(R,1)}-\rho _{(L,1)}|} = \tfrac{1}{2}$. The density profiles and currents are shown in Fig. 5 for two additional values of $\epsilon$, one in the “mild” downhill regime $J>0$ for $\epsilon = 0.75$ (left panels), the other in the “mild” uphill regime $J<0$ for $\epsilon = 0.25$ (right panels). In the uphill regime (right panel), i.e., when $\epsilon =0.75$, the “mild" non-linearity of the total density profile is already visible, indicating the violation of Fick’s law.

Identification of the uphill regime We define the notion of uphill current below and identify the parameter ranges for which uphill diffusion occurs.

Definition 3.17

(Uphill diffusion) For parameters $\rho _{(L,0)},\rho _{(L,1)},\rho _{(R,0)},\rho _{(R,1)}$ and $\epsilon >0,$ we say the system has an uphill current in stationarity if the total current J and the difference between the total density of particles in the right and the left side of the system given by $\rho _R - \rho _L$ have the same sign, where it is understood that $\rho _R = \rho _{(R,0)}+\rho _{(R,1)}$ and $\rho _L = \rho _{(L,0)}+\rho _{(L,1)}$.

$\square$

Proposition 3.18

(Uphill regime) Let $a_0 : = \rho _{(R,0)}-\rho _{(L,0)}$ and $a_1:= \rho _{(R,1)}-\rho _{(L,1)}$. Then the macroscopic system admits an uphill current in stationarity if and only if

$$\begin{aligned} a_0^2+(1+\epsilon )\,a_0a_1+\epsilon a_1^2 < 0. \end{aligned}$$

(3.86)

If, furthermore, $\epsilon \in [0,1]$, then

• (i) either

  $$\begin{aligned} a_0+a_1> 0 \text { with } a_0<0,\,a_1> 0 \end{aligned}$$

  or

  $$\begin{aligned} a_0+a_1< 0 \text { with } a_0 > 0,\,a_1 < 0, \end{aligned}$$

• (ii) $\epsilon \in \big [0,-\tfrac{a_0}{a_1}\big ]$.

Proof

Note that, by (3.78), there is an uphill current if and only if $a_0 + a_1$ and $a_0 + \epsilon a_1$ have opposite signs. In other words, this happens if and only if

$$\begin{aligned} (a_0+a_1)(a_0+\epsilon \,a_1) = a_0^2+(1+\epsilon )\,a_0a_1+\epsilon a_1^2<0. \end{aligned}$$

The above constraint forces $a_0a_1<0$. Further simplification reduces the parameter regime to the following four cases:

• $a_0+a_1 > 0$ with $a_0<0,\,a_1> 0$ and $\epsilon <-\tfrac{a_0}{a_1}$,

• $a_0+a_1 < 0$ with $a_0>0,\,a_1< 0$ and $\epsilon <-\tfrac{a_0}{a_1}$,

• $a_0+a_1 > 0$ with $a_0>0,\,a_1< 0$ and $\epsilon >-\tfrac{a_0}{a_1}$,

• $a_0+a_1 < 0$ with $a_0<0,\,a_1> 0$ and $\epsilon >-\tfrac{a_0}{a_1}$.

Under the assumption $\epsilon \in [0,1]$, only the first two of the above four cases survive. $\square$

3.6 The Width of the Boundary Layer

We have seen that for $\epsilon =0$ the microscopic density profile of the fast particles $\theta _0(x)$ linearly interpolates between $\rho _{L,0}$ and $\rho _{R,0}$, whereas the density profile of the slow particles satisfies $\theta _1(x) = \theta _0(x)$ for all $x\in \{2,\ldots ,N-1\}$. In the macroscopic setting this produces a continuous macroscopic profile ${\rho _0^{\mathrm{{stat}}}}(y) = \rho _{L,0} + (\rho _{R,0}-\rho _{L,0})y$ for the bottom-layer, while the top-layer profile develops two discontinuities at the boundaries when either $\rho _{(L,0)}\ne \rho _{(L,1)}$ or $\rho _{(R,0)}\ne \rho _{(R,1)}$. In particular,

$$\begin{aligned} {\rho _1^{\mathrm{{stat}}}}(y)\rightarrow \big [\rho _{L,0} + (\rho _{R,0}-\rho _{L,0})y\big ]\, {\mathbf {1}}_{(0,1)}(y) + \rho _{L,1} {\mathbf {1}}_{\{1\}}(y) + \rho _{R,1} {\mathbf {1}}_{\{0\}}(y),\quad \epsilon \downarrow 0, \end{aligned}$$

for $y\in [0,1]$. For small but positive $\epsilon ,$ the curve is smooth and the discontinuity is turned into a boundary layer. In this section we investigate the width of the left and the right boundary layers as $\epsilon \downarrow 0$. To this end, let us define

$$\begin{aligned} W_L:=|\rho _{(L,0)}-\rho _{(L,1)}|,\quad W_R:=|\rho _{(R,0)}-\rho _{(R,1)}|. \end{aligned}$$

(3.87)

Note that, the profile $\rho _1$ develops a left boundary layer if and only if $W_L > 0$ and, similarly, a right boundary layer if and only if $W_R > 0$.

Definition 3.19

We say that the left boundary layer is of size $f_L(\epsilon )$ if there exists $C>0$ such that, for any $c>0,$

$$\begin{aligned} \lim _{\epsilon \downarrow 0} \frac{R_L(\epsilon , c)}{f_L(\epsilon )}=C, \end{aligned}$$

where $R_L(\epsilon , c)=\sup \left\{ y\in \big (0,\tfrac{1}{2}\big ): \left| \frac{d^2}{d y^2}{\rho _1^{\mathrm{{stat}}}}(y)\right| \ge c\right\}$. Analogously, we say that the right boundary layer is of size $f_R(\epsilon )$ if there exists $C>0$ such that, for any $c>0,$

$$\begin{aligned} \lim _{\epsilon \downarrow 0} \frac{1-R_R(\epsilon , c)}{f_R(\epsilon )}=C, \end{aligned}$$

where $R_R(\epsilon , c)=\inf \left\{ y\in \big (\tfrac{1}{2},1\big ): \left| \frac{d^2}{d y^2}{\rho _1^{\mathrm{{stat}}}}(y)\right| \ge c\right\}$.

The widths of the two boundary layers essentially measure the deviation of the top-layer density profile (and therefore also the total density profile) from the bulk linear profile corresponding to the case $\epsilon = 0$. In the following proposition we estimate the sizes of the two boundary layers.

Proposition 3.20

(Width of boundary layers) The widths of the two boundary layers are given by

$$\begin{aligned} f_L(\epsilon ) = f_R(\epsilon ) = \sqrt{\epsilon }\,\log (1/\epsilon ), \end{aligned}$$

(3.88)

where $f_L(\epsilon ),f_R(\epsilon )$ are defined as in Definition 3.19.

Proof

Note that, to compute $f_L(\epsilon )$, it suffices to keep $W_L>0$ fixed and put $W_R = 0$, where $W_L,W_R$ are as in (3.87). Let ${\overline{y}}(\epsilon , c)\in (0,\tfrac{1}{2})$ be such that, for some constant $c>0$,

$$\begin{aligned} \left| \frac{d^2}{d y^2}{\rho _1^{\mathrm{{stat}}}}(y)\right| \ge c, \end{aligned}$$

(3.89)

or equivalently, since $\epsilon \Delta \rho _1 =\Upsilon (\rho _1-\rho _0)$,

$$\begin{aligned} |{\rho _1^{\mathrm{{stat}}}}(y)-{\rho _0^{\mathrm{{stat}}}}(y)|\ge \frac{c\epsilon }{\Upsilon }. \end{aligned}$$

(3.90)

Recalling the expressions of ${\rho _0^{\mathrm{{stat}}}}(\cdot )$ and ${\rho _1^{\mathrm{{stat}}}}(\cdot )$ for positive $\epsilon$ given in (3.39)−(3.40), we get

$$\begin{aligned} \left| \frac{\sinh \big [\sqrt{\Upsilon (1+\tfrac{1}{\epsilon })}(1-y)\big ]}{\sinh \big [\sqrt{\Upsilon (1+\tfrac{1}{\epsilon })}\big ]}\,(\rho _{(L,0)}-\rho _{(L,1)})+\frac{\sinh \big [\sqrt{\Upsilon (1+\tfrac{1}{\epsilon })}\,y\big ]}{\sinh \big [\sqrt{\Upsilon (1+\tfrac{1}{\epsilon })}\big ]}\,(\rho _{(R,0)}-\rho _{(R,1)})\right| \ge \frac{c\epsilon }{\Upsilon }. \end{aligned}$$

(3.91)

Using (3.87) plus the fact that $W_R = 0,$ and setting $B_{\epsilon ,\Upsilon }:=\sqrt{\Upsilon \left( 1+\tfrac{1}{\epsilon }\right) }$, we see that

$$\begin{aligned} \sinh \left[ B_{\epsilon ,\Upsilon }(1-y)\right] \ge \frac{c\epsilon }{\Upsilon W_L}\sinh \left[ B_{\epsilon ,\Upsilon }\right] . \end{aligned}$$

(3.92)

Because $\sinh (\cdot )$ is strictly increasing, (3.92) holds if and only if

$$\begin{aligned} {\overline{y}}(\epsilon , c) \le 1 - \frac{1}{B_{\epsilon ,\Upsilon }}\sinh ^{-1}\left[ \frac{c\epsilon }{\Upsilon W_L}\sinh \left( \tfrac{B_{\epsilon ,\Upsilon }}{2}\right) \right] . \end{aligned}$$

(3.93)

Thus, for small $\epsilon >0$ we have

$$\begin{aligned} R_L(\epsilon ,c) = 1 - \frac{1}{B_{\epsilon ,\Upsilon }}\sinh ^{-1}\left[ \frac{c\epsilon }{\Upsilon W_L}\sinh \left( \tfrac{B_{\epsilon ,\Upsilon }}{2}\right) \right] , \end{aligned}$$

(3.94)

where $R_L(\epsilon , c)$ is defined as in Definition 3.19. Since $\sinh ^{-1} x = \log (x+\sqrt{x^2+1})$ for $x\in {{\mathbb {R}}}$, we obtain

$$\begin{aligned} \begin{aligned} R_L(\epsilon , c)&= \frac{\sqrt{\epsilon }}{\sqrt{\Upsilon (1+\epsilon )}}\log \left[ \frac{N_{\epsilon ,\Upsilon }+\sqrt{N_{\epsilon ,\Upsilon }^2+1}}{\epsilon CN_{\epsilon ,\Upsilon }+\sqrt{(\epsilon CN_{\epsilon ,\Upsilon })^2+1}}\right] \\&= \frac{\sqrt{\epsilon }}{\sqrt{\Upsilon (1+\epsilon )}}\log (1/\epsilon )+\frac{\sqrt{\epsilon }}{\sqrt{\Upsilon (1+\epsilon )}}\log \left[ \frac{1+\sqrt{1+(1/N_{\epsilon ,\Upsilon })^2}}{C+\sqrt{C^2+(1/(\epsilon N_{\epsilon ,\Upsilon }))^2}}\right] \\&=\frac{\sqrt{\epsilon }}{\sqrt{\Upsilon (1+\epsilon )}}\log (1/\epsilon ) + R_{\epsilon ,\Upsilon ,W_L}, \end{aligned} \end{aligned}$$

(3.95)

where $N_{\epsilon ,\Upsilon }:=\sinh \Big (\tfrac{B_{\epsilon ,\Upsilon }}{2}\Big ), C:=\tfrac{c}{\Upsilon W_L}$, and the error term is

$$\begin{aligned} R_{\epsilon ,\Upsilon ,W_L}:=\frac{\sqrt{\epsilon }}{\sqrt{\Upsilon (1+\epsilon )}}\log \left[ \frac{1+\sqrt{1+(1/N_{\epsilon ,\Upsilon })^2}}{C+\sqrt{C^2+(1/(\epsilon N_{\epsilon ,\Upsilon }))^2}}\right] . \end{aligned}$$

Note that, since $\epsilon N_{\epsilon ,\Upsilon }\rightarrow \infty$ as $\epsilon \downarrow 0$, we have

$$\begin{aligned} \lim \limits _{\epsilon \downarrow 0}\frac{R_{\epsilon ,\Upsilon ,W_L}}{\sqrt{\epsilon }} = \frac{1}{\sqrt{\Upsilon }}\log (1/C) < \infty . \end{aligned}$$

(3.96)

Hence, combining (3.95)−(3.96), we get

$$\begin{aligned} \lim \limits _{\epsilon \downarrow 0}\frac{R_L(\epsilon , c)}{\sqrt{\epsilon }\log (1/\epsilon )} = \lim \limits _{\epsilon \downarrow 0}\frac{1}{\sqrt{\Upsilon }(1+\epsilon )}+\lim \limits _{\epsilon \downarrow 0}\frac{R_{\epsilon ,\Upsilon ,W_L}}{\sqrt{\epsilon }\log (1/\epsilon )} = \frac{1}{\sqrt{\Upsilon }} \end{aligned}$$

(3.97)

and so, by Definition 3.19, $f_L(\epsilon ) = \sqrt{\epsilon }\log (1/\epsilon )$.

Similarly, to compute $f_R(\epsilon )$, we first fix $W_L = 0, W_R>0$ and note that, for some $c>0$, we have, by using (3.91),

$$\begin{aligned} |\partial ^2{\rho _1^{\mathrm{{stat}}}}(y)|\ge c\quad \text { if and only if }\quad \sinh \left[ B_{\epsilon ,\Upsilon }\,y\right] \ge \tfrac{c\epsilon }{\Upsilon W_R}\sinh \left[ B_{\epsilon ,\Upsilon }\right] . \end{aligned}$$

(3.98)

Hence, by appealing to the strict monotonicity of $\sinh (\cdot ),$ we obtain

$$\begin{aligned} R_R(\epsilon ,c)=\inf \left\{ y\in \big (\tfrac{1}{2},1\big ): \left| \frac{d^2}{d y^2}{\rho _1^{\mathrm{{stat}}}}(y)\right| \ge c\right\} = \frac{1}{B_{\epsilon ,\Upsilon }}\sinh ^{-1}\left[ \frac{c\epsilon }{\Upsilon W_R}\sinh \left( \tfrac{B_{\epsilon ,\Upsilon }}{2}\right) \right] . \end{aligned}$$

(3.99)

Finally, by similar computations as in (3.95)–(3.97), we see that

$$\begin{aligned} \lim \limits _{\epsilon \downarrow 0}\frac{1-R_R(\epsilon ,c)}{\sqrt{\epsilon \log (1/\epsilon )}} = \frac{1}{\sqrt{\Upsilon }} \end{aligned}$$

(3.100)

and hence $f_R(\epsilon )=\sqrt{\epsilon }\log (1/\epsilon )$. $\square$

Inverse of the Boundary-Layer Matrix

The inverse of the matrix $M_\epsilon$ defined in (3.30) is given by ($\alpha _1$ and $\alpha _2$ are as in (3.31))

$$\begin{aligned} M_\epsilon ^{-1}:= \frac{1}{Z} \begin{bmatrix} -m_{13} &{}\quad -m_{14} &{}\quad m_{13} &{}\quad m_{14}\\ m_{21} &{}\quad m_{22} &{}\quad m_{23} &{}\quad m_{24}\\ m_{31}(\alpha _2) &{}\quad m_{32}(\alpha _2) &{}\quad m_{33}(\alpha _2) &{}\quad m_{34}(\alpha _2)\\ -m_{31}(\alpha _1) &{}\quad -m_{32}(\alpha _1) &{}\quad -m_{33}(\alpha _1) &{}\quad -m_{34}(\alpha _1) \end{bmatrix} , \end{aligned}$$

(A.1)

where

$$\begin{aligned} \begin{aligned} Z&:= \alpha _1^{N + 1} [\alpha _2 (1 - \epsilon ) (\alpha _2^{N - 1} + 1) + 2 \epsilon (\alpha _2^{N + 1} + 1)]\,[\alpha _2 (1 + N) (1 - \epsilon ) (\alpha _2^{N - 1} - 1) \\&\qquad + 2 \epsilon (N + \epsilon ) (\alpha _2^{1 + N} - 1)],\\ m_{13}&:=\alpha _1^{N + 1}[\alpha _2 (1 - \epsilon ) (\alpha _2^{N - 1} + 1) + 2 \epsilon (\alpha _2^{N + 1} + 1)]\,[\alpha _2 (1 - \epsilon ) (\alpha _2^{N - 1} - 1) + \epsilon (\alpha _2^{N + 1} - 1)],\\ m_{14}&:=\epsilon \, \alpha _1^{ N + 1}[\alpha _2 (1 - \epsilon ) (\alpha _2^{N - 1} + 1) + 2 \epsilon (\alpha _2^{N + 1} + 1)]\,(\alpha _2^{N+1} - 1),\\ m_{21}&:= (1 + N) (1 - \epsilon )^2 (\alpha _2^{N-1}-\alpha _1^{N-1})-\epsilon (1 - \epsilon )^2(\alpha _2 - \alpha _1)\\&\qquad + \epsilon ^2 (1 + 2 N + \epsilon )(\alpha _2^{N+1}-\alpha _1^{N+1}) + \epsilon (1 - \epsilon )(2 + 3 N + \epsilon )(\alpha _2^N-\alpha _1^N),\\ m_{22}&:= \epsilon \,[(1 - \epsilon )(1 + N)(\alpha _2^N-\alpha _1^N) + \epsilon (1 + 2 N + \epsilon )(\alpha _2^{N+1}-\alpha _1^{N+1})],\\ m_{23}&:= \epsilon \,(1 - \epsilon ) [(N + \epsilon )(\alpha _2 - \alpha _1) - (1 - \epsilon )(\alpha _2^N - \alpha _1^N) - \epsilon (\alpha _2^{N+1} - \alpha _1^{N+1})],\\ m_{24}&:= -\epsilon (1 - \epsilon ) [(1 + N) (\alpha _2 - \alpha _1) + \epsilon \,(\alpha _2^{N+1} - \alpha _1^{N+1})], \end{aligned} \end{aligned}$$

(A.2)

and the polynomials $m_{31}(z),m_{32}(z),m_{33}(z),m_{34}(z)$ are defined as

$$\begin{aligned} \begin{aligned} m_{31}(z)&:= -(1 -\epsilon )^2\,z - \epsilon \,(1 - \epsilon ) + (1 - \epsilon ) (N + \epsilon )\,z^N - \epsilon (1 - 2 N - 3 \epsilon )\,z^{N+1},\\ m_{32}(z)&:= -(1 - \epsilon )(1 + N) z^N - \epsilon \,(1 - \epsilon ) - \epsilon (1 + 2 N + \epsilon )\,z^{N+1},\\ m_{33}(z)&:= (1 -\epsilon )^2\,z^N + \epsilon \,(1 - \epsilon )\,z^{N+1} - (1 - \epsilon ) (N + \epsilon )\,z + \epsilon (1 - 2 N - 3 \epsilon ),\\ m_{34}(z)&:= (1 + N)(1 - \epsilon )\,z + \epsilon \,(1 - \epsilon )\,z^{N+1} + \epsilon (1 + 2 N + \epsilon ). \end{aligned} \end{aligned}$$

(A.3)

We remark that most of the terms appearing in the inverse simplify because of (3.32). We define the four vectors $\vec {c}_1,\vec {c}_2,\vec {c}_3,\vec {c}_4$ as the respective rows of $M_\epsilon ^{-1}$, i.e.,

$$\begin{aligned} \begin{aligned} \vec {c}_1&:= (M_\epsilon ^{-1})^T \vec {e}_1,\quad \vec {c}_2 := (M_\epsilon ^{-1})^T \vec {e}_2,\\ \vec {c}_3&:= (M_\epsilon ^{-1})^T \vec {e}_3,\quad \vec {c}_4 := (M_\epsilon ^{-1})^T \vec {e}_4, \end{aligned} \end{aligned}$$

(A.4)

where

$$\begin{aligned} \begin{aligned} \vec {e}_1&:= \big [ \begin{array}{c c c c} 1&0&0&0 \end{array} \big ]^T,&\vec {e}_{2} :=\big [ \begin{array}{c c c c} 0&1&0&0 \end{array} \big ]^T,\\ \vec {e}_{3}&:= \big [ \begin{array}{c c c c} 0&0&1&0 \end{array} \big ]^T,&\vec {e}_{4} := \big [ \begin{array}{c c c c} 0&0&0&1 \end{array} \big ]^T. \end{aligned} \end{aligned}$$