Exact Steady-State Distributions of Multispecies Birth–Death–Immigration Processes: Effects of Mutations and Carrying Capacity on Diversity

Abstract

Stochastic models that incorporate birth, death and immigration (also called birth–death and innovation models) are ubiquitous and applicable to many problems such as quantifying species sizes in ecological populations, describing gene family sizes, modeling lymphocyte evolution in the body. Many of these applications involve the immigration of new species into the system. We consider the full high-dimensional stochastic process associated with multispecies birth–death–immigration and present a number of exact and asymptotic results at steady state. We further include random mutations or interactions through a carrying capacity and find the statistics of the total number of individuals, the total number of species, the species size distribution, and various diversity indices. Our results include a rigorous analysis of the behavior of these systems in the fast immigration limit which shows that of the different diversity indices, the species richness is best able to distinguish different types of birth–death–immigration models. We also find that detailed balance is preserved in the simple noninteracting birth–death–immigration model and the birth–death–immigration model with carrying capacity implemented through death. Surprisingly, when carrying capacity is implemented through the birth rate, detailed balance is violated.

Appendices

Mathematical Appendices

A: Simple Birth–Death–Immigration Models (sBDI)

1.1 A.1: Finite Number of Species

So far, we have assumed immigration events introduce completely new species to the system, regardless of the existing population structure. Within the context of island biodiversity, this assumption corresponds to the mainland hosting an unlimited number of species, so that individuals who emigrate to the island are always part of a new species. Mathematically, we are assuming that each species immigrates only once.

In this Appendix, we consider an alternative model where the number of mainland species Q is finite. In this case, the probability that a newly immigrated individual belongs to species i (with $1\le i\le Q$) is 1 / Q and the number of species in the island cannot exceed Q. As a consequence, the total number of species $C \le Q$, and the number of species with k individuals $c_{k}\le Q$ for all k.

The dynamics of the total number of individuals N remains unchanged with respect to the sBDI model, as the type of species immigrating from the mainland does not affect overall birth or death rates. Therefore, the distribution for P(N) remains identical to the one derived in Eq. (5) for the simple BDI model. We can now determine the distribution of $\vec {c}$ in the alternative model using the same approach taken for the sBDI model. Transitions are given by

Note that the birth process rate is effectively augmented by $\alpha /Q$, due to the possibility of a new individual immigrating into an existing species. Conversely, the corresponding immigration rate for new species is decreased by $\alpha C/Q$. Also note that the limit $Q \rightarrow \infty$ reduces the current model to the original sBDI. Using detailed balanced equations, similarly as in the sBDI model, we can write $P(\vec {c})$ as follows

$$\begin{aligned} P(\vec {c})=\left( 1-\frac{r}{\mu }\right) ^{\alpha /r}\frac{Q!}{\left( Q-C\right) !} \left( \frac{r}{\mu }\right) ^{N} \left( \frac{1}{\prod _{i=1}^{\infty }c_{i}!}\right) \prod _{\ell =1}^{\infty }\prod _{j=0}^{\ell -1} \left( \frac{j+\frac{\alpha }{Qr}}{j+1}\right) ^{c_{\ell }}. \end{aligned}$$

One can verify that this distribution satisfies all the required transition equations. Yet, contrary to the sBDI model, it is more difficult to determine the distributions of C, $c_{k}$ and $n_{i}$ based on this formulation; in particular the factor $Q!/\left( Q-C\right) !$ prevents us from applying the same mathematical procedure used in the sBDI case.

We can however take a different route, namely invoking neutrality and the independence of the system, to deduce the distributions of C and $c_{k}$. Since each species behaves independently from all others, we can consider the number $m_{i}$ of individuals in the $i^\mathrm{th}$ species (with $1\le i\le Q$) independently from the rest. Note that $m_{i}$ is a random variable that can be zero when there are no individuals of species i present in the system. The quantity $m_i$ is the counterpart to $n_{i}$ introduced for the sBDI model with the caveat that $n_i$ represents the number of individuals of a species actually present on the island (i.e. $P\left( n_{i}=0\right) =0$). In the current model $n_{i}$ can be expressed as a function of $m_i$ via

$$\begin{aligned} P\left( n_{i}=k\right) =P\left( m_{i}=k|m_{i}>0\right) \qquad \text {for }k\ge 1, \end{aligned}$$

(40)

describing the distribution of the $i^\mathrm{th}$ species provided that at least one of its individuals is on the island. The random variable $m_{i}$ follows a birth and death process: its birth rate is $\alpha /Q+rm_{i}$ and its death rate is $\mu m_{i}$. The $\alpha /Q$ rate corresponds to immigration, the rate $r m_{i}$ corresponds to actual reproduction. We already determined the steady state distribution of this process in Eq. (5), yielding a negative binomial distribution with parameters $\alpha /(rQ)$ and $r/\mu$ as follows

$$\begin{aligned} P(m_{i})=\left( 1-\frac{r}{\mu }\right) ^{\alpha /\left( Qr\right) } \left( \frac{r}{\mu }\right) ^{m_{i}}\frac{1}{m_{i}!}\prod _{k=0}^{m_{i}-1} \left( \frac{\alpha }{Qr}+k\right) . \end{aligned}$$

The $P(n_i)$ distribution can be determined from $P(m_i)$ expressed above, using Eq. (40)

$$\begin{aligned} P\left( n_{i}=k\right)= & {} \frac{P\left( m_{i}=k\right) }{1-P\left( m_{i}=0\right) }= \frac{\left( 1-\frac{r}{\mu }\right) ^{\alpha /\left( Qr\right) }}{1-\left( 1-\frac{r}{\mu }\right) ^{\alpha /\left( Qr\right) }} \left( \frac{r}{\mu }\right) ^{k} \frac{1}{k!}\prod _{k'=0}^{k-1} \left( \frac{\alpha }{Qr}+k'\right) \qquad \\&\text {for any }k\ge 1. \end{aligned}$$

Finally, the number of species $c_{k}$ with k individuals and the total number of species C can be expressed as a function of $m_{i}$ as follows

$$\begin{aligned} c_{k}=\sum _{i=1}^{Q}I\left( m_{i}=k\right) \quad \text {and}\quad C=\sum _{i=1}^{Q}I\left( m_{i}>0\right) . \end{aligned}$$

Since all $m_{i}$ are i.i.d., the probability distributions of $c_{k}$ and C are given by

$$\begin{aligned} P(c_{k})&=\left( {\begin{array}{c}Q\\ c_{k}\end{array}}\right) P\left( m_{i}=k\right) ^{c_{k}}\left( 1-P\left( m_{i}=k\right) \right) ^{Q-c_{k}},\\ P(C)&=\left( {\begin{array}{c}Q\\ C\end{array}}\right) \left( 1-P\left( m_{i}=0\right) \right) ^{C}P\left( m_{i}=k\right) ^{Q-C}, \end{aligned}$$

which are binomial distributions of respective parameters Q and $P\left( m_{i}=k\right)$ for $c_{k}$, and Q and $1-P\left( m_{i}=0\right)$ for C. Note that this approach does not allow us to determine the diversity indices H and S.

1.2 A.2: Convergences in the Large Immigration Regime

In this section, we will prove the convergence of

$$\begin{aligned} N/\Omega ,\quad C/\Omega ,\quad \left( \frac{c_{1}}{\Omega }, \frac{c_{2}}{\Omega },\ldots \right) ,\quad \text {and}\quad H/\log \Omega \end{aligned}$$

in the large immigration regime defined by $\alpha = \widetilde{\alpha }\Omega$, $\Omega \rightarrow \infty$.

Proposition 1

The scaled total number of individuals $N/\Omega$ converges in distribution to the constant $\widetilde{\alpha }/(\mu -r)$.

Proof

The definition of the convergence in distribution described in Eq. (3) is equivalent to the convergence of its moment generating function. One is left with showing that

$$\begin{aligned} \text {for any }\xi <0,\quad \lim _{\Omega \rightarrow \infty }\mathbb {E}\left[ e^{\xi N/\Omega }\right] =\frac{\widetilde{\alpha }}{\mu -r} \end{aligned}$$

(see for instance [5, Chapter 5]). Since $N\sim \text {NegBinom}\left( \widetilde{\alpha }\Omega /r,r/\mu \right)$ for which the moment generating function is known, we have for any $\xi <0$:

$$\begin{aligned} \mathbb {E}\left[ e^{\xi N/\Omega }\right]&= \left( \frac{1-r/\mu }{1-e^{\xi /\Omega }r/\mu }\right) ^{\widetilde{\alpha }\Omega /r}. \end{aligned}$$

Upon taking the logarithm of the previous expression, we find

$$\begin{aligned} \log \left[ \mathbb {E}\left[ e^{\xi N/\Omega }\right] \right]&=\frac{\widetilde{\alpha }\Omega }{r} \left[ \log \left( 1-r/\mu \right) -\log \left( 1-e^{\xi /\Omega }r/\mu \right) \right] \\&\quad \times \, \mathop {\sim }\limits _{\Omega \rightarrow \infty }-\frac{\widetilde{\alpha }\Omega }{r} \log \left[ 1-\frac{\xi }{\Omega }\frac{r/\mu }{1-r/\mu }\right] \\&\quad \times \,\mathop {\sim }\limits _{\Omega \rightarrow \infty }\frac{\widetilde{\alpha }\Omega }{r} \frac{\xi }{\Omega }\frac{r/\mu }{1-r/\mu } = \xi \frac{\widetilde{\alpha }}{\mu -r}, \end{aligned}$$

so

thus proving the proposition. $\square$

Proposition 2

The scaled total number of species $C/\Omega$ converges in distribution to

Proof

The proof is similar to Proposition 1. $\square$

Proposition 3

For each $k>0$, $c_{k}/\Omega$ converges in distribution to

Proof

For any vector $\vec {c}$ and $k\ge 1$, we have that

$$\begin{aligned} c_{k}=\sum _{i=1}^{C}\varvec{I}\left( n_{i},k\right) . \end{aligned}$$

Consider the moment generating function of the random variable $c_{k}$. For any $\xi <0$, we have

$$\begin{aligned} \mathbb {E}\left[ e^{\xi c_{k}/\Omega }\right] =\mathbb {E}\left[ \exp \left( \frac{\xi }{\Omega }\sum _{i=1}^{C}\varvec{I}\left( n_{i},k\right) \right) \right] . \end{aligned}$$

Since $n_{i}$ are identical and independently distributed and independent of C, and since their distributions do not depend on the parameter $\Omega$, it follows that

$$\begin{aligned} \mathbb {E}\left[ e^{\xi c_{k}/\Omega }\right]&=\mathbb {E}\left[ \left( \mathbb {E}\left[ \exp \left( \frac{\xi }{\Omega }\varvec{I}\left( n_{1},k\right) \right) \right] \right) ^{C}\right] \\&=\mathbb {E}\left[ \left( e^{\xi /\Omega } P(n_{1}=k) + \left( 1-P(n_{1}=k)\right) \right) ^{C}\right] \\&=\mathbb {E}\left[ \left( \left( e^{\xi /\Omega }-1\right) P(n_{1}=k)+1\right) ^{C}\right] . \end{aligned}$$

Since the probability distribution of $n_{1}$ is known, we have

$$\begin{aligned} \mathbb {E}\left[ e^{\xi c_{k}/\Omega }\right]&=\mathbb {E}\left[ \left( 1-{1\over k}\left( {r \over \mu }\right) ^{k}\, \frac{(e^{\xi /\Omega }-1)}{\log (1-r/\mu )}\right) ^{C}\right] . \end{aligned}$$

Note that for any real A,

$$\begin{aligned} C\log \left[ 1-\left( e^{\xi /\Omega }-1\right) A\right]&\mathop {\sim }\limits _{\Omega \rightarrow \infty }-C\left( e^{\xi /\Omega }-1\right) A,\\&\mathop {\sim }\limits _{\Omega \rightarrow \infty }-{C\over \Omega }\xi A. \end{aligned}$$

Considering the exponential of this expression, we have

$$\begin{aligned} \mathbb {E}\left[ e^{\xi c_{k}/\Omega }\right] =\mathbb {E}\left[ \exp \left[ -{C\over \Omega }\frac{(r/\mu )^{k}}{k}\, \frac{\xi }{\log (1-r/\mu )}\right] \right] . \end{aligned}$$

Finally, since we have already shown that $C/\Omega$ converges in distribution (Proposition 2 above), we find

$$\begin{aligned} \lim _{\Omega \rightarrow \infty }\mathbb {E}\left[ e^{\xi c_{k}/\Omega }\right] = \exp \left( \xi \frac{\widetilde{\alpha }}{r}\,\frac{(r/\mu )^{k}}{k}\right) . \end{aligned}$$

$\square$

Proposition 4

The Shannon’s Entropy H converges in distribution as

Proof

Using the definition of H,

$$\begin{aligned} {H\over \log \Omega }=\sum _{k=1}^{\infty }k\,\frac{c_{k}}{\Omega }\, \frac{\Omega }{N}\frac{\log N-\log k}{\log \Omega }, \end{aligned}$$

where $c_{k}/\Omega$ and $N/\Omega$ converge in distribution to known constants, we find

$\square$

Proposition 5

The Simpson’s diversity index S converges in distribution as

Proof

By the definition of S (Eq. (2))

$$\begin{aligned} S=1 - \frac{1}{\Omega }\sum _{k=1}^{\infty }\frac{c_{k}}{\Omega }\left( \frac{k}{N/\Omega }\right) ^{2}, \end{aligned}$$

and since $c_{k}/\Omega$ and $N/\Omega$ converge in distribution to known constants, we find

One can then recognize the power series identity

$$\begin{aligned} \frac{r/\mu }{(1-r/\mu )^{2}}=\sum _{k=1}^{\infty }k\,\left( \frac{r}{\mu }\right) ^{k} \end{aligned}$$

and hence show that the second term vanishes as $\Omega \rightarrow \infty$ and deduce the result . $\square$

Fig. 6

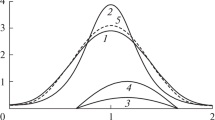
Distribution of the number of individuals in one species $n_{i}$ under different parameter choices. Dots represent simulations for various values of $u=\alpha /r$, $v=r/\mu$, ($r=1$) and $\epsilon$; solid lines depict logarithmic distributions with parameter $r(1-\epsilon )/\mu$. As expected, the logarithmic distributions match the simulations $n_{i}$, and the distributions of $n_{i}$ do not depend on u

Fig. 7

Accuracy of Shannon’s entropy and Simpson’s index (as defined in Eq. (25)). We plot the ratio of the estimates of Shannon’s entropy and Simpson’s index and their respective values measured via simulation for different $u=\alpha /r$, $v=r/\mu$ (by taking $r=1$), and different $\epsilon$. The estimates become more accurate as $\mathbb {E}\left[ N\right]$ increases: the error is below $10\%$ for any parameters u, v, $\epsilon$ such that $\mathbb {E}\left[ N\right]$ is larger than 5

B: BDI Model with Mutation (BDIM)

1.1 B.1: Distribution of the Number of Individual in One Species

We propose an argument for a Log-series distribution of any species

$$\begin{aligned} \pi _{k}=P(n_{i}=k) \end{aligned}$$

when all species are independent of each other. There are several ways to interpret $\pi _{k}$. First consider the explicit dynamics of each species. Denote by $m_{q}(t)$ the number of individuals of species q at time t and define $a_{q}$ as the time of arrival (by convention, we order the species such as $a_{0}=0<a_{1}<a_{2}<\ldots$) and $d_{q}$ its “lifespan”, i.e. the species will be extinct at time $a_{q}+d_{q}$ (see the example in Fig. 8a). Note that the index q indicates the order of arrival (and not the species identity index i used in the main article), and that the distribution of the times $a_{q}$ is not specified and can be adapted to any rate of species creation (either by immigration or by mutation). The evolution of each species is independent of each other, and each of them defines an identically distributed birth–death process characterized by the following transitions

$$\begin{aligned} {\left\{ \begin{array}{ll} m_{q}\rightarrow m_{q}+1 &{} \text {at rate }m_{q}\,r(1-\epsilon ),\\ m_{q}\rightarrow m_{q}-1 &{} \text {at rate }m_{q}\,\mu . \end{array}\right. } \end{aligned}$$

(41)

Due to the $r<\mu$ assumption, this process will become extinct almost surely [2, Chapter 2] and the lifespan $d_{q}$ of each species is finite (Figs. 6 and 7).

Fig. 8

a A representative trajectory of three immigrated species. The q-th species is introduced at time $a_{q}$ and extinguishes at time $a_{q}+d_{q}$. b Construction of the process $\overline{m}$ (defined in Eq. (43)) by stacking and concatenating the trajectories of each species $\left( m_{q}\right) _{q\in \mathbb {N}}$

In the main article, we interpreted $\pi _{k}$ as the number of individuals in a given species at steady state, that is to say, we considered the $T\rightarrow \infty$ limit

$$\begin{aligned} \pi _{k}=\lim _{T\rightarrow \infty }P\left( m_{J_{T}}(T)=k\right) \end{aligned}$$

where $J_{T}$ is the index of a randomly sampled species among those that exist at time T; i.e., $J_{T}$ is uniformly chosen among all the species q such that $a_{q}<T<a_{q}+d_{q}$.

However, there is another way to interpret $\pi _{k}$. Consider all species that exist or have existed up to time T and then randomly select one of them, species $I_{T}$. The number of individuals in species $I_{T}$ at a randomly chosen time $\tau _{I_{T}}$ between the introduction of the species (at time $a_{I_{T}}$) and the extinction (at time $a_{I_{T}}+d_{I_{T}}$) is denoted $m_{I_{T}}$. In this picture, we can characterize $\pi _{k}$ according to

$$\begin{aligned} \pi _{k}=\lim _{T\rightarrow \infty }P\left( m_{I_{T}}(\tau _{I_{T}})=k\right) . \end{aligned}$$

(42)

The main difference between the two approaches is that, in the first case, we sample among the species that exist at a precise time T before taking $T\rightarrow \infty$, while in the second case, we sample among all the species that existed before time T (before taking $T\rightarrow \infty$).

For a fixed time T, the last species introduced in the system is given by

$$\begin{aligned} Q_{T}=\mathop {\text {argmax}}\limits _{q\in \mathbb {N}}\left( a_{q}<T\right) . \end{aligned}$$

All species that exist or have existed before time T are in the set $\left\{ 0,\ldots ,Q_{T}\right\}$. Note that since $a_{q}$ are increasing in q, $\lim _{T\rightarrow \infty } Q_{T}=\infty$. As per Eq. (42), we have to sample one species among the set $\left\{ 0,\ldots ,Q_{T}\right\}$. One key point is that the random selection is not uniform: there is a higher chance of selecting species with longer lifespans. If $I_{T}$ is the index of the randomly chosen species, we can write

$$\begin{aligned} P\left( I_{T}=q\right) =\varvec{I}\left( q\le Q_{T}\right) \frac{d_{q}}{\sum _{j=0}^{Q_{T}}d_{j}}. \end{aligned}$$

The first term $\varvec{I}\left( q\le Q_{T}\right)$ ensures that the species q exists before time T while the second term proportionally weights the probability of sampling according to their lifespans. Conditioned on species $I_{T}$ having been sampled, we then randomly chose a time $\tau _{I_{T}}$ uniformly distributed between $a_{I_{T}}$ and $a_{I_{T}}+d_{I_{T}}$.

Proposition 6

The limiting distribution becomes

$$\begin{aligned} \pi _{k}=\lim _{T\rightarrow \infty }P\left( m_{I_{T}}(\tau _{I_{T}})=k\right) = \frac{1}{\log \left( 1-\frac{r(1-\epsilon )}{\mu }\right) } \frac{1}{k}\left( \frac{r(1-\epsilon )}{\mu }\right) ^{k}. \end{aligned}$$

Proof

By summing over all possible species q, we can write

$$\begin{aligned} P\left( m_{I_{T}}(\tau _{I_{T}})=k\right)&=\sum _{q\in \mathbb {N}}\mathbb {E}\left[ \varvec{I}\left( q\le Q_{T}\right) \frac{d_{q}}{\sum _{j=0}^{Q_{T}}d_{j}}\varvec{I}\left( m_{q}(\tau _{q}),k\right) \right] \\&=\mathbb {E}\left[ \sum _{q=0}^{Q_{T}}\frac{d_{q}}{\sum _{j=0}^{Q_{T}}d_{j}} \frac{1}{d_{q}}\int _{a_{q}}^{a_{q}+d_{q}}\varvec{I}\left( m_{q}(t),k\right) \,\mathrm{d}t\right] \\&=\mathbb {E}\left[ \frac{\sum _{q=0}^{Q_{T}}\int _{a_{q}}^{a_{q}+d_{q}}\varvec{I}\left( m_{q}(t),k\right) \,\mathrm{d}t}{\sum _{j=0}^{Q_{T}}d_{j}}\right] \end{aligned}$$

Next, consider the process $\overline{m}(s)$ defined as

$$\begin{aligned} \overline{m}(t)=m_{\nu _{t}}\left( t-\overline{d}_{\nu (t)}+a_{\nu (t)}\right) \end{aligned}$$

(43)

with

$$\begin{aligned} \overline{d}_{k}=\sum _{q=1}^{k-1}d_{q}\quad \text {and}\quad \nu (t)=\mathop {\text {argmax}}\limits _{q}\left\{ \sum _{j=0}^{q}d_{j}<t\right\} . \end{aligned}$$

The process $\overline{m}$ is simply the stacking of all the processes $m_{q}$ in the sense that the process $\overline{m}(t)$ for t between $\overline{d}_{q}$ and $\overline{d}_{q+1}$ will be equal to the process $m_{q}(s)$ for $s=t-\overline{d}_{q}+a_{q}$ between $a_{q}$ and its extinction time $a_{q}+d_{q}$ (see the example on Fig. 8b). With this stacked process,

$$\begin{aligned} P\left( m_{I_{T}}(\tau _{I_{T}})=k\right)&=\mathbb {E}\left[ \frac{\int _{0}^{a_{\delta _{T}}+d_{\delta _{T}}} \varvec{I}\left( \overline{m}(t),k\right) \,\mathrm{d}t}{\overline{d}_{Q_{T}}}\right] . \end{aligned}$$

By ergodicity of the process $\overline{m}$, we have

$$\begin{aligned} \lim _{T\rightarrow \infty }P\left( m_{I_{T}}(\tau _{I_{T}})=k\right) =\lim _{T\rightarrow \infty }P\left( \overline{m}(T)=k\right) . \end{aligned}$$

Finally, we have to determine the steady state of the process $\overline{m}$. Since the transitions of the process $\overline{m}$ are a simple birth–death process

$$\begin{aligned} {\left\{ \begin{array}{ll} \overline{m}\rightarrow \overline{m}+1 &{} \text {at rate }\quad \overline{m}\,r(1-\epsilon )\\ \overline{m}\rightarrow \overline{m}-1 &{} \text {at rate }\quad \overline{m}\,\mu \varvec{I}\left( \overline{m}>0\right) . \end{array}\right. }, \end{aligned}$$

(44)

we have that its equilibrium distribution is a logarithmic series distribution with parameter $p\equiv r(1-\epsilon )/\mu$ (by imposing equations of detailed balance). $\square$

1.2 B.2: Moments of C

The third relation of Eq. (1) yields the following expression for the moment generating function of N:

$$\begin{aligned} \mathbb {E}\left[ e^{\xi N}\right] =\mathbb {E}\left[ \prod _{i=1}^{C}e^{\xi n_{i}}\right] , \end{aligned}$$

for any $\xi <0$. Since all the $\left( n_{i}\right) _{i\le C}$ are identical and independently distributed and independent of C, we have

$$\begin{aligned} \mathbb {E}\left[ e^{\xi N}\right]&=\mathbb {E}\left[ \mathbb {E}\left[ e^{\xi n_{1}}\right] ^{C}\right] = \mathbb {E}\left[ \left( \frac{\log \left( 1-pe^{\xi }\right) }{\log \left( 1-p\right) }\right) ^{C}\right] . \end{aligned}$$

(45)

Equation (20) shows that the distribution over $n_{1}$ is a log-series distribution with parameter $p=r\left( 1-\epsilon \right)$. By redefining the variable $\xi '$ such that $e^{\xi '}:=\log \left( 1-pe^{\xi }\right) /\log \left( 1-p\right)$ and eliminating $\xi$ for $\xi '$, Eq. (45) becomes an expression for the moment generating function of C,

$$\begin{aligned} \mathbb {E}\left[ e^{\xi 'C}\right] =\left( \frac{1-r/\mu }{1-\frac{r}{\mu } \frac{1-\left( 1-p\right) ^{e^{\xi '}}}{p}}\right) ^{\alpha /r}. \end{aligned}$$

By differentiating this expression, we can determine the second moment of C:

$$\begin{aligned} \mathbb {E}\left[ C^{2}\right]&=\lim _{\xi '\rightarrow 0}\frac{\mathrm{d}^{2}}{\mathrm{d}\xi '^{2}}\mathbb {E}\left[ e^{\xi 'C}\right] = \mathbb {E}\left[ C\right] \left[ 1+\log \left( 1-p\right) + \left( 1+\frac{r}{\alpha }\right) \mathbb {E}\left[ C\right] \right] , \end{aligned}$$

which yields the expression for $\text {var}\left[ C\right]$ in Eq. (22).

C: BDI Model with Carrying Capacity (BDICC)

1.1 C.1: Steady State Distribution of $\vec {c}$

To determine $P(\vec {c})$, the probability of occurrence of the species-count state $\vec {c}$, first consider a finite $K=\mathop {\text {argmax}}\limits _{i}(c_{i}>0)$. As explained in the main text, if the system is reversible, one instance of Eq. (27) is

$$\begin{aligned} \mu (N)c_{K}K P(\vec {c})= (K-1)\left( c_{K-1}+1\right) r P(c_{1},\ldots ,c_{K-1}+1,c_{K}-1,\vec {0}). \end{aligned}$$

Recursively unwinding this relationship, we find

$$\begin{aligned} P(\vec {c})&=P(c_{1},\ldots ,c_{K-1}+1,c_{K}-1,\vec {0}) \frac{r}{\mu (N)}\frac{K-1}{K}\frac{c_{K-1}+1}{c_{K}},\\ P(\vec {c})&=P(c_{1},\ldots ,c_{K-1}+c_{K},0,\vec {0}) \frac{r^{c_{K}}}{\mu (N)\ldots \mu (N-c_{K}+1)}\left( \frac{K-1}{K}\right) ^{c_{K}} \frac{\left( c_{K-1}+c_{K}\right) !}{c_{K}!c_{K-1}!},\\ P(\vec {c})&=P(C,\vec {0})\frac{r^{N-C}}{\mu (N)\ldots \mu (N-(K-1)c_{K}-\ldots -c_{2}+1)} \prod _{i=1}^{K-1}\prod _{j=i+1}^{K}\left( \frac{i}{i+1}\right) ^{c_{j}} \frac{C!}{\prod _{i=1}^{K}c_{i}!},\\ P(\vec {c})&=P(C,\vec {0})\frac{r^{N-C}}{\prod _{n=1}^{N-C}\mu (N-n+1)} \frac{C!}{\prod _{i=1}^{K}i^{c_{i}}c_{i}!}. \end{aligned}$$

After applying Eq. (28), we have by recursion

$$\begin{aligned} P(C,0,\ldots )=\frac{\alpha }{\mu (C)}\frac{1}{C}P(C-1,0,\ldots ) =\frac{\alpha ^{C}}{C!\prod _{i=1}^{C}\mu (i)}P(0,\ldots ), \end{aligned}$$

and

$$\begin{aligned} P(\vec {c})=P(0,\ldots )\left( \frac{\alpha }{r}\right) ^{C} \frac{r^{N}}{\prod _{n=1}^{N}\mu (n)}\frac{1}{\prod _{i=1}^{K}i^{c_{i}}c_{i}!}. \end{aligned}$$

Since the state $\vec {c}=\vec {0}$ uniquely corresponds to the state $N=0$ and the above expression holds for K arbitrarily large, it follows that

$$\begin{aligned} P(\vec {c})=\frac{1}{Z_{\alpha ,r,\mu }}\left( \frac{\alpha }{r}\right) ^{C} \frac{r^{N}}{\prod _{n=1}^{N}\mu (n)}\frac{1}{\prod _{i=1}^{\infty }i^{c_{i}}c_{i}!}. \end{aligned}$$

(46)

One can verify that this steady-state distribution satisfies the detailed balanced conditions connecting all pairs of states:

$$\begin{aligned} {\left\{ \begin{array}{ll} \mu \left( \sum _{k}kc_{k}\right) kc_{k}P(\vec {c})= (k-1)\left( c_{k-1}+1\right) r P(c_{1}, \ldots , c_{k-1}+1,c_{k}-1, \ldots ) &{} \forall k>1, \\ \mu \left( \sum _{k}kc_{k}\right) c_{1}P(\vec {c})=\alpha P(c_{1}-1,\ldots , c_{k}, \ldots ). \end{array}\right. } \end{aligned}$$

(47)

1.2 C.2: Convergence of $N/\Omega$

Theorem 7

The random variable $N/\Omega$ converges in probability to the real $n^{*}$ which is the only solution of the fixed point Eq. (36).

To prove this Theorem, first define

$$\begin{aligned} f(x):=\frac{\widetilde{\alpha }+rx}{x\widetilde{\mu }(x)}\quad \text {and} \quad f_{k}:= \frac{\widetilde{\alpha }+(k-1)r/\Omega }{(k/\Omega ) \widetilde{\mu }(k/\Omega )} \,\quad \forall k\in \mathbb {N}_{*}. \end{aligned}$$

The function f defines the steady-state constraint on $n=N/\Omega$ given by Eq. (36) where $x=n^{*}$ is the only real solution to $f(x)=1$. With these definitions, the probability distribution over N can be expressed as

$$\begin{aligned} \forall n\in \mathbb {N},\qquad P\left( N=n\right) = \frac{\exp \left( \sum _{k=1}^{n}\log f_{k}\right) }{\sum _{n'=0}^{\infty }\exp \left( \sum _{k=1}^{n'}\log f_{k}\right) }. \end{aligned}$$

Now, consider the following lemma:

Lemma 8

The function f is strictly decreasing and there exists a $\Omega ^{*}$ for which $\,\forall \Omega \ge \Omega ^{*}$, $\left( f_{k}\right) _{k\ge 1}$ is a decreasing sequence.

Proof

The decrease of the function f is a direct implication of the increase of $\widetilde{\mu }$. For, $\left( f_{k}\right) _{k\ge 1}$ we have

$$\begin{aligned} \left( k+1\right) \left( \widetilde{\alpha }\Omega +r(k-1)\right) -k\, \left( \widetilde{\alpha }\Omega +r k\right) =\widetilde{\alpha }\Omega -r, \end{aligned}$$

which is positive for large enough $\Omega$. Since $\widetilde{\mu }$ is increasing,

$$\begin{aligned} \frac{f_{k}}{f_{k+1}}= \frac{\widetilde{\mu }(\left( k+1\right) /\Omega )}{\widetilde{\mu }(k/\Omega )} \frac{\left( k+1\right) \left( \widetilde{\alpha }\Omega +(k-1)r\right) }{k\,\left( \widetilde{\alpha }\Omega +r k\right) }>1. \end{aligned}$$

$\square$

To prove Theorem 7, we have to show that $\forall \delta >0$,

that is to say, we have to show that

(48)

(49)

The proofs of convergence for both limits above are very similar so we will focus on the proof of Eq. (48). To simplify notation, we define $a_{\Omega ,\delta } \equiv \left\lceil \Omega \left( n^{*}+\delta \right) \right\rceil$, (where $\left\lceil \cdot \right\rceil$ is the ceiling function). Since the distribution of N is known, we have

$$\begin{aligned} P\left( N/\Omega > n^{*}+\delta \right)&= \frac{\sum _{n=a_{\Omega ,\delta }}^{\infty } \exp \left( \sum _{k=1}^{n}\log f_{k}\right) }{\sum _{n=0}^{a_{\Omega ,\delta }-1} \exp \left( \sum _{k=1}^{n}\log f_{k}\right) +\sum _{n=a_{\Omega ,\delta }}^{\infty } \exp \left( \sum _{k=1}^{n}\log f_{k}\right) }\\&=\left( \frac{\sum _{n=0}^{a_{\Omega ,\delta }-1} \exp \left( \sum _{k=1}^{n}\log f_{k}\right) }{\sum _{n=a_{\Omega ,\delta }}^{\infty } \exp \left( \sum _{k=1}^{n}\log f_{k}\right) }+1\right) ^{-1}. \end{aligned}$$

Thus, it is enough to show

in order to prove the convergence of Eq. (48).

Proposition 9

In the $\Omega \rightarrow \infty$ limit, the following equivalence holds

$$\begin{aligned} \sum _{n=a_{\Omega ,\delta }}^{\infty } \exp \left( \sum _{k=1}^{n}\log f_{k}\right) \mathop {\sim }\limits _{\Omega \rightarrow \infty }\exp \left( \sum _{k=1}^{a_{\Omega ,\delta }-1} \log f_{k}\right) \frac{1}{1-f(n^{*}+\delta )} \end{aligned}$$

Proof

We first decompose the sum according to

$$\begin{aligned} \sum _{n=a_{\Omega ,\delta }}^{\infty }\exp \left( \sum _{k=1}^{n} \log f_{k}\right)&=\exp \left( \sum _{k=1}^{a_{\Omega ,\delta }-1} \log f_{k}\right) \sum _{n=a_{\Omega ,\delta }}^{\infty } \exp \left( \sum _{k=a_{\Omega ,\delta }}^{n}\log f_{k}\right) . \end{aligned}$$

The second term of the decomposition can be rewritten as

$$\begin{aligned} \sum _{n=a_{\Omega ,\delta }}^{\infty } \exp \left( \sum _{k=a_{\Omega ,\delta }}^{n}\log f_{k}\right) = \sum _{n=0}^{\infty }\exp \left( \sum _{k=0}^{n}\log f_{k+a_{\Omega ,\delta }}\right) . \end{aligned}$$

Since , it follows that

$$\begin{aligned} \sum _{k=0}^{n}\log f_{k+a_{\Omega ,\delta }} \mathop {\sim }\limits _{\Omega \rightarrow \infty }n\,\log f(n^{*}+\delta ). \end{aligned}$$

As f is a strictly decreasing function (cf. Lemma 8), and since $n^{*}$ is the only point where $f(n^{*})=1$, it follows that $f\left( n^{*}+\delta \right) <1$. Therefore, the sum over n converges, and we have

$$\begin{aligned} \sum _{n=a_{\Omega ,\delta }}^{\infty } \exp \left( \sum _{k=a_{\Omega ,\delta }}^{n}\log f_{k}\right) \mathop {\sim }\limits _{\Omega \rightarrow \infty }\frac{1}{1-f(n^{*}+\delta )} \end{aligned}$$

$\square$

With the previous Proposition, it is enough to prove that the ratio

$$\begin{aligned} \frac{\sum _{n=0}^{a_{\Omega ,\delta }-1} \exp \left( \sum _{k=1}^{n}\log f_{k}\right) }{\exp \left( \sum _{k=1}^{a_{\Omega ,\delta }-1} \log f_{k}\right) }=\sum _{n=0}^{a_{\Omega ,\delta }-1} \exp \left( -\sum _{k=n+1}^{a_{\Omega ,\delta }-1}\log f_{k}\right) \end{aligned}$$

diverges to infinity in order to prove the convergence of Eq. (48).

Proposition 10

The sum

diverges.

Proof

Since $\left( f_{k}\right) _{k\ge 1}$ is decreasing for large $\Omega$ (cf. Lemma 8), we have

$$\begin{aligned} \sum _{k=n+1}^{a_{\Omega ,\delta }-1}\log f_{k}\le \left( a_{\Omega ,\delta }-n-1\right) \log f_{a_{\Omega ,\delta }-1} \end{aligned}$$

for sufficiently large $\Omega$. Therefore,

$$\begin{aligned} \sum _{n=0}^{a_{\Omega ,\delta }-1}\exp \left( -\sum _{k=n+1}^{a_{\Omega ,\delta }-1} \log f_{k}\right) \ge \sum _{n'=1}^{a_{\Omega ,\delta }} \left( \frac{1}{f_{a_{\Omega ,\delta }-1}}\right) ^{n'}. \end{aligned}$$

Since

for large enough $\Omega$ and since f is decreasing, we have that $f_{a_{\Omega ,\delta }-1}<1-\eta$ for $\eta$ small enough. Therefore, we conclude the divergence

and proof of the proposition. $\square$

With this Proposition, we have proven the convergence of Eq. (48). The convergence of Eq. (49) can be proved using exactly the same methods by considering $b_{\Omega ,\delta }= \left\lfloor \Omega \left( \delta +n^{*}\right) \right\rfloor$ instead of $a_{\Omega ,\delta }$.

1.3 C.3: Convergence of $C/\Omega$

Theorem 11

The scaled total number of species $C/\Omega$ converges in distribution to

in which $n^{*}$ is the only real solution of the fixed point Eq. (36).

Proof

One has to prove that

with

$$\begin{aligned} Z_{\alpha ,r,\mu }= \sum _{n'=0}^{\infty }\exp \left( \sum _{k=1}^{n'} \log \frac{\widetilde{\alpha }+r(k-1)/\Omega }{k/\Omega \,\widetilde{\mu }(k/\Omega )}\right) . \end{aligned}$$

First note that

$$\begin{aligned} \mathbb {E}\left[ \exp \left[ \xi C/\Omega \right] \right]&= \frac{1}{Z_{\alpha ,r,\mu }}\sum _{n=0}^{\infty } \exp \left( \sum _{k=1}^{n} \log \frac{\widetilde{\alpha }e^{\xi /\Omega }+r (k-1)/\Omega }{k/\Omega \,\widetilde{\mu }(k/\Omega )}\right) \\&=\sum _{n=0}^{\infty }P\left( N=n\right) \exp \left( \sum _{k=1}^{n} \log \frac{\widetilde{\alpha }e^{\xi /\Omega }+r(k-1)/\Omega }{\widetilde{\alpha }+r (k-1)/\Omega }\right) \\&=\mathbb {E}\left[ \exp \left( \sum _{k=1}^{N}\log \frac{\widetilde{\alpha }e^{\xi /\Omega }+r (k-1)/\Omega }{\widetilde{\alpha }+r (k-1)/\Omega }\right) \right] \end{aligned}$$

Since $N/\Omega$ converges in probability to $n^{*}$,

$$\begin{aligned} \mathbb {E}\left[ \exp \left[ \xi C/\Omega \right] \right] \mathop {\sim }\limits _{\Omega \rightarrow \infty } \exp \left( \sum _{k=1}^{n^{*}\Omega } \log \frac{\widetilde{\alpha }e^{\xi /\Omega }+r (k-1)/\Omega }{\widetilde{\alpha }+r(k-1)/\Omega }\right) . \end{aligned}$$

Since the function $\log \left( \frac{\widetilde{\alpha }e^{\xi /\Omega }+r \left( x-1\right) /\Omega }{\widetilde{\alpha }+r \left( x-1\right) /\Omega }\right)$ is decreasing in x, we can bound the sum with its lower and upper integral bounds

$$\begin{aligned} \int _{1}^{n^{*}\Omega +1}\log \frac{\widetilde{\alpha }e^{\xi /\Omega }+(x-1)r/\Omega }{\widetilde{\alpha }+(x-1)r/\Omega }\,\mathrm{d}x\le & {} \sum _{k=1}^{n^{*}\Omega }\log \frac{\widetilde{\alpha }e^{\xi /\Omega }+(k-1)r/\Omega }{\widetilde{\alpha }+(k-1)r/\Omega }\\\le & {} \frac{\xi }{\Omega }+\int _{1}^{n^{*}\Omega }\log \frac{\widetilde{\alpha }e^{\xi /\Omega }+(x-1)r/\Omega }{\widetilde{\alpha }+(x-1)r/\Omega }\,\mathrm{d}x. \end{aligned}$$

After rescaling $y = (x-1)/\Omega$, the bounds can be expressed as

$$\begin{aligned} \Omega \int _{0}^{n^{*}+1/\Omega }\log \frac{\widetilde{\alpha }e^{\xi /\Omega }+r y}{\widetilde{\alpha }+r y}\,\mathrm{d}y\le & {} \sum _{k=1}^{n^{*}\Omega }\log \frac{\widetilde{\alpha }e^{\xi /\Omega }+ (k-1)r/\Omega }{\widetilde{\alpha }+(k-1)r/\Omega }\\\le & {} \frac{\xi }{\Omega }+\Omega \int _{0}^{n^{*}}\log \frac{\widetilde{\alpha }e^{\xi /\Omega }+r y}{\widetilde{\alpha }+r y}\,\mathrm{d}y \end{aligned}$$

Upon taking $\Omega \rightarrow \infty$ and expanding the above expression, we find that both bounds converge to

$$\begin{aligned} \xi \int _{0}^{n^{*}}\frac{\widetilde{\alpha }}{\widetilde{\alpha }+r y}\,\mathrm{d}y. \end{aligned}$$

Thus, we find

$$\begin{aligned} \mathbb {E}\left[ \exp \left[ \xi C/\Omega \right] \right]&\mathop {\sim }\limits _{\Omega \rightarrow \infty } \exp \left( \xi \widetilde{\alpha }\,\int _{0}^{n^{*}} \frac{1}{\widetilde{\alpha }+r u}\,\mathrm{d}u\right) = \exp \left( \xi \frac{\widetilde{\alpha }}{r}\, \log \left[ 1+\frac{r}{\widetilde{\alpha }} n^{*}\right] \right) . \end{aligned}$$

$\square$

1.4 C.4: Convergence of $n_{i}$

Proposition 12

The marginal probability over each particle count $n_{i}$ converges according to

Proof

The $n_{i}$ values are identically distributed, so that for any $i,j\le C$,

$$\begin{aligned} \text {for any }k\ge 1,\quad P\left( n_{i}=k\right) =P\left( n_{j}=k\right) . \end{aligned}$$

We can then compute the expectation

$$\begin{aligned} \mathbb {E}\left[ \frac{c_{k}}{C}\right] =\mathbb {E}\left[ \sum _{i=1}^{C}\frac{\mathbb {E}\left[ \varvec{I}\left( n_{i},k\right) |C\right] }{C}\right] =\mathbb {E}\left[ \mathbb {E}\left[ \varvec{I}\left( n_{1},k\right) |C\right] \right] =P\left( n_{1}=k\right) . \end{aligned}$$

This expectation is over a product of two converging quantities:

$$\begin{aligned} \mathbb {E}\left[ \frac{c_{k}}{C}\right] =\mathbb {E}\left[ \frac{c_{k}}{\Omega }\,\frac{\Omega }{C}\right] = P(n_{1}=k), \end{aligned}$$

where $c_{k}/\Omega$ and $C/\Omega$ converge in distribution to constants

We now apply the mapping theorem (see [5, Chapter 5]) to $\mathbb {E}\left[ g\left( \frac{c_{k}}{\Omega },\frac{C}{\Omega }\right) \right]$ for any continuous function g to obtain

$\square$

1.5 C.5: Explicit Breakdown of Detailed Balance in the BDICC-bis Model with Birth-Mediated Carrying Capacity

Here, we consider a birth–death–immigration model with carrying capacity but contrary to the BDICC model presented in Fig. 1c, the carrying capacity is on the birth rate r(N), and the death rate $\mu$ is a constant. By analogy with the BDICC analysis, we find a sufficient condition for a steady state to exist

$$\begin{aligned} \lim _{N\rightarrow \infty }r(N)<\mu . \end{aligned}$$

The distribution P(N) of the total number of individuals is given by

$$\begin{aligned} P(N) ={\left\{ \begin{array}{ll} \displaystyle \frac{1}{Z_{\alpha ,\mu }},\quad N=0,\\ \displaystyle \frac{1}{Z_{\alpha ,\mu }} \frac{1}{N!}{\displaystyle \prod _{k=0}^{N-1}} \frac{\alpha +r(k) k}{\mu }, \quad N\ge 1, \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned} Z_{\alpha ,\mu }=1+\sum _{N=1}^{\infty }\frac{1}{N!} {\displaystyle \prod _{k=0}^{N-1}}\frac{\alpha +r(k) k}{\mu }. \end{aligned}$$

All possible transitions of the BDICC-bis model are given by

If we assume detailed balance between pairs of states with maximum clone size K, we can recurse the relations

$$\begin{aligned} \mu c_{k}kP(c_{1},\ldots ,c_{k-1},c_{k},\ldots )= r(N)(k-1)\left( c_{k-1}+1\right) P(c_{1},\ldots ,c_{k-1}+1,c_{k}-1,\ldots ) \end{aligned}$$

for $2\le k\le K$ down to the states

$$\begin{aligned} \mu c_{1} P(c_{1},\vec {0}) =\alpha P(c_{1}-1,\vec {0}) \end{aligned}$$

to give

$$\begin{aligned} P(\vec {c})=\frac{1}{Z_{\alpha ,\mu }}\frac{\alpha ^{C}}{\mu ^{N}} \frac{\prod _{n=1}^{N-C}r(N-n)}{\prod _{i=1}^{\infty }i^{c_{i}}c_{i}!}. \end{aligned}$$

(50)

Using these chosen pairs of states to impose detailed balance, we find a unique distribution $P(\vec {c})$. However, this form of $P(\vec {c})$ will not obey detailed balance between all pairs of states. For example, balancing the transitions

would also require

$$\begin{aligned} \mu c_{1}P(c_{1},c_{2}\ge 1,\ldots ) = \alpha P(c_{1}-1,c_{2}\ge 1,\ldots ). \end{aligned}$$

However, using the $P(\vec {c})$ from Eq. (50), we find

$$\begin{aligned} \frac{\mu c_{1}P(c_{1},c_{2}\ge 1,\ldots )}{\alpha P(c_{1}-1,c_{2}\ge 1,\ldots )}= \frac{r(C-1)}{r(N-1)} \ne 1 \end{aligned}$$

because generally, $N\ne C$. Remarkably, the analogous exercise for the BDICC model where $\mu = \mu (N)$ does satisfy detailed balance between all pairs of states and the $P(\vec {c})$ we derived for the BDICC model, Eq. (29), is exact.