Power Spectrum of a Noisy System Close to a Heteroclinic Orbit

Abstract

We consider a two-dimensional dynamical system that possesses a heteroclinic orbit connecting four saddle points. This system is not able to show self-sustained oscillations on its own. If endowed with white Gaussian noise it displays stochastic oscillations, the frequency and quality factor of which are controlled by the noise intensity. This stochastic oscillation of a nonlinear system with noise is conveniently characterized by the power spectrum of suitable observables. In this paper we explore different analytical and semianalytical ways to compute such power spectra. Besides a number of explicit expressions for the power spectrum, we find scaling relations for the frequency, spectral width, and quality factor of the stochastic heteroclinic oscillator in the limit of weak noise. In particular, the quality factor shows a slow logarithmic increase with decreasing noise of the form $Q\sim [\ln (1/D)]^2$. Our results are compared to numerical simulations of the respective Langevin equations.

Appendices

Appendix A: Details on the Numerical Determination of the Spectrum from the Fokker–Planck Equation (Matrix-Inversion Method)

In Sect. 3 we derived two partial differential equations that determine the power spectrum. Here we show how these equations can be solved numerically by an eigenfunction expansion (for further details, see [6]).

1.1 Expansion into a Complete set of Functions

The power spectrum $S_{z z}(\omega )$ is given in Eq. 9 in terms of an auxiliary function $\tilde{H}(\varvec{\mathbf {y}};\omega )$, which is defined in Eq. 10 and satisfies the two-dimensional, second-order, partial differential equations,

$$\begin{aligned} {{\mathrm{\mathcal {L}_{\text {FP}}}}}(\varvec{\mathbf {y}}) P_0(\varvec{\mathbf {y}})&=0, \qquad \qquad \qquad \qquad \qquad \quad (7 \,\mathrm{revisited}) \\ \left( {{\mathrm{\mathcal {L}_{\text {FP}}}}}(\varvec{\mathbf {y}})+i\omega \mathcal {I}\right) \tilde{H}(\varvec{\mathbf {y}};\omega )&=-P_0(\varvec{\mathbf {y}})\left[ f(\varvec{\mathbf {y}}) - \langle f(\varvec{\mathbf {y}}) \rangle \right] , \qquad (11\, \mathrm{revisited}) \end{aligned}$$

where $P_0(\varvec{\mathbf {y}})$ is the stationary probability distribution and ${{\mathrm{\mathcal {L}_{\text {FP}}}}}$ is the Fokker–Planck operator associated to $\varvec{\mathbf {y}}(t)$. The solution to this system of partial differential equations may be found by expanding $P_0(\varvec{\mathbf {y}})$ and $\tilde{H}(\varvec{\mathbf {y}};\omega )$ into an appropriate basis of functions that satisfy the boundary conditions.

The heteroclinic oscillator system Eq. 1 with reflecting boundary conditions on the domain $\Omega =[-\pi /2,\pi /2]\times [-\pi /2,\pi /2]$ can be shown to be equivalent (for certain observables $f(\varvec{\mathbf {y}})$, such as $z_i=\sin (y_i)$) to a system with periodic boundary conditions on $\Omega '=[-\pi ,\pi ]\times [-\pi ,\pi ]$ and the same dynamics. Thus, we expand the solutions into the basis of harmonic functions with period $L_i=2\pi$ in both $y_1$ and $y_2$, i.e.

$$\begin{aligned} P_0(\varvec{\mathbf {y}})=\sum _{m=-\infty }^{\infty }\sum _{l=-\infty }^{\infty }c_{m,l}e^{i(k_1 m y_1+k_2 l y_2)}=\sum _{m=-\infty }^{\infty }\sum _{l=-\infty }^{\infty }c_{m,l}e^{i(my_1+ly_2)}. \qquad (12\, \mathrm{revisited}) \end{aligned}$$

and, similarly,

$$\begin{aligned} \tilde{H}(\varvec{\mathbf {y}};\omega )=\sum _{m=-\infty }^{\infty }\sum _{l=-\infty }^{\infty }\tilde{H}_{m,l}(\omega )e^{i(my_1+ly_2)}. \qquad \qquad (13\, \mathrm{revisited}) \end{aligned}$$

Inserting Eq. 12 into Eq. 7, grouping the terms associated to each basis function $e^{imy_1}e^{ily_2}$, and requiring that these terms should vanish for every combination m, l, we obtain for the coefficients of the steady state distribution

$$\begin{aligned} 0=&-\frac{1}{4}\Big [(m-l)c_{m-1,l-1}+(m+l)c_{m+1,l-1}-(m-l)c_{m+1,l+1} \nonumber \\&-(m+l)c_{m-1,l+1}+2\alpha m c_{m-2,l}+2\alpha l c_{m,l-2}\nonumber \\&-2\alpha m c_{m+2,l}-2\alpha l c_{m,l+2}+4D(m^2+l^2)c_{m,l}\Big ],\quad \forall m,l\in \mathbb {Z}. \end{aligned}$$

(A1)

Additional symmetries present in the system impose further constraints on the set of coefficients $\{c_{m,l}\}$: (i) because ${{\mathrm{\mathcal {L}_{\text {FP}}}}}(-\varvec{\mathbf {y}})={{\mathrm{\mathcal {L}_{\text {FP}}}}}(\varvec{\mathbf {y}})$ the density is symmetric under inversion, $P_0(-\varvec{\mathbf {y}})=P_0(\varvec{\mathbf {y}})$, from which we find $c_{-m,-l}=c_{m,l}$; (ii) ${{\mathrm{\mathcal {L}_{\text {FP}}}}}(\varvec{\mathbf {y}})$ is also invariant under the translations $(y_1, y_2)\mapsto (y_1+2\pi k, y_2)$ and $(y_1, y_2)\mapsto (y_1, y_2+2\pi k)$, from which we can infer that $c_{m,l}=0$ if $m+l=2k+1,k\in \mathbb {Z}$; (iii) because $P_0(\varvec{\mathbf {y}})$ is real-valued, $c_{-m,-l}=c_{m,l}^*$. Finally, from the normalization condition follows $c_{0,0}=\pi ^{-2}$.

If we insert the expansions Eqs. 13 and 12 into Eq. 11 with $f(y_1)=\sin (y_1)$ and follow the derivation for $P_0(\varvec{\mathbf {y}})$ above, we obtain

$$\begin{aligned}&-\frac{1}{4}\left[ (m-l)\tilde{H}_{m-1,l-1}\right. +(m+l)\tilde{H}_{m+1,l-1}-(m-l)\tilde{H}_{m+1,l+1}-(m+l)\tilde{H}_{m-1,l+1}\nonumber \\&\quad \quad \quad +\,2\alpha l \tilde{H}_{m,l-2} \left. +\,2\alpha m \tilde{H}_{m-2,l}-2\alpha m \tilde{H}_{m+2,l}-2\alpha l \tilde{H}_{m,l+2}\right. \nonumber \\&\quad \quad \quad \left. +\left( 4D(m^2+l^2) - 4i\omega \right) \tilde{H}_{m,l}\right] \nonumber \\&\quad =\frac{1}{2i}\left[ (2\pi )^2c_{m,l}(c_{1,0}-c_{-1,0})-(c_{m-1,l}-c_{m+1,l})\right] ,\quad \forall m,l\in \mathbb {Z}. \end{aligned}$$

(A2)

This defines an infinite inhomogeneous system of linear equations. From the underlying symmetries of the problem follow further conditions on the coefficients (see Table 1).

Table 1 Summary of the conditions imposed by symmetries (other than $2\pi$-periodicity on $y_1$ and $y_2$) on the auxiliary function $\tilde{H}(\varvec{\mathbf {y}};\omega )$ and its expansion coefficients $\tilde{H}(\omega )$

Finally, to obtain the power spectrum $S_{zz}(\omega )$ in terms of the coefficients, we plug Eq. 13 into Eq. 9 and use the orthogonality relations for the Fourier basis:

$$\begin{aligned} S_{xx}(\omega )=2(2\pi )\mathfrak {R}{\left[ \sum _m \tilde{H}_{m, 0}\int dy_1 f(y_1)e^{imy_1}\right] }. \end{aligned}$$

Choosing our observable to be $z=f(y_1)=\sin (y_1)=(e^{iy_1}-e^{-iy_1})/(2i)$ and using $\tilde{H}_{m, l}=-\tilde{H}_{-m,-l}$ leads to

$$\begin{aligned} S_{xx}(\omega )=2(2\pi )^2\mathfrak {R}{\left[ i\tilde{H}_{0,1}(\omega )\right] }=-8\pi ^2\mathfrak {I}{\left[ \tilde{H}_{0,1}(\omega )\right] }, \quad \quad \qquad (14\, \mathrm{revisited}) \end{aligned}$$

where $\mathfrak {I}[\cdot ]$ denotes the imaginary part of the argument.

1.2 Solving the Full Linear System

We start by solving the system Eq. A2 for the coefficients $c_{m,l}$ of the expansion of $P_0(\varvec{\mathbf {y}})$; this allows us to construct Eq. A2, which is then solved for the coefficients $\tilde{H}_{m,l}(\omega )$ of the expansion of $\tilde{H}(\varvec{\mathbf {y}};\omega )$ at each $\omega$. From there, the power spectrum Eq. 14 is evaluated.

In the first place, we truncate the set of basis functions $\{e^{imy_1}e^{ily_2}\}, -L\le m,l\le L$ and choose a specific ordering of its elements, according to which the coefficients $c_{m,l}$ (resp. $\tilde{H}_{m,l}(\omega )$) are arranged into a column vector $\varvec{\mathbf {c}}$ (resp. $\varvec{\mathbf {h}}_{\omega }$) which looks as follows

$$\begin{aligned} \varvec{\mathbf {c}}^{(L)}= \begin{bmatrix} c_{-L,-L}, \ldots , c_{-L,L},&\cdots ,&c_{0,-L}, \ldots ,c_{0,L},&\ldots ,&c_{L,-L}, \cdots ,c_{L,L} \end{bmatrix}^{T}, \end{aligned}$$

where $^T$ denotes transposition and $\varvec{\mathbf {c}}^{(L)}$ indicates that the size of $\varvec{\mathbf {c}}$ depends on the truncation parameter L. Note that each entry of $\varvec{\mathbf {c}}^{(L)}$ corresponds to a coefficient $c_{m,l}$ associated to a basis function $e^{imy_1}e^{ily_2}$, i.e.

$$\begin{aligned} \left[ \varvec{\mathbf {c}}^{(L)}\right] _{m(2L+1)+l}=c_{m,l},\quad -L\le m,l \le L. \end{aligned}$$

One can define $\varvec{\mathbf {h}}_{\omega }$ analogously. The chosen ordering is also used to set the elements of the matrices $\varvec{\mathbf {M}}$ and $\varvec{\mathbf {A}}_{\omega }$ of coefficients of the linear systems Eqs. A1 and A2, as well as the inhomogeneity $\varvec{\mathbf {f}}$ on the RHS of Eq. A2.

With the previous ingredients we can write the equivalent of Eqs. 7 and 11 in matrix form as

$$\begin{aligned} \varvec{\mathbf {M}}^{(L)}(D,\alpha ) \varvec{\mathbf {c}}^{(L)}&= 0, \end{aligned}$$

(A3)

$$\begin{aligned} \varvec{\mathbf {A}}_{\omega }^{(L)}(D,\alpha ;\omega ) \varvec{\mathbf {h}}_{\omega }^{(L)}&= \varvec{\mathbf {f}}^{(L)}, \end{aligned}$$

(A4)

where we have indicated the dependences of $\varvec{\mathbf {M}}$ and $\varvec{\mathbf {A}}_{\omega }$ on the noise intensity D, the stability parameter $\alpha$ and the frequency at which we evaluate the power spectrum $\omega$. After solving Eq. A3 once, we can determine $\varvec{\mathbf {f}}$ and solve Eq. A4 for $\varvec{\mathbf {h}}_{\omega }$ at a set of discrete frequencies $\{\omega _i\},i\in {1,\dots ,N}$ to evaluate the power spectrum $S(\omega )$ in a given frequency window.

The applicability of the numerical method outlined above is limited by the size of the matrices $\varvec{\mathbf {M}}^{(L)}$ and $\varvec{\mathbf {A}}_{\omega }^{(L)}$, which is determined by the truncation parameter L. In particular, the dimension of $\varvec{\mathbf {M}}^{(L)}$ and $\varvec{\mathbf {A}}_{\omega }^{(L)}$ grows as $(2L+1)^2\times (2L+1)^2$, thus even small values of L yield large matrices. Solving linear systems described by large matrices is memory- and CPU-demanding. However, the use of efficient sparse matrix methods ($\varvec{\mathbf {M}}^{(L)}$ and $\varvec{\mathbf {A}}_{\omega }^{(L)}$ have very few non-zero entries) may alleviate these problems.

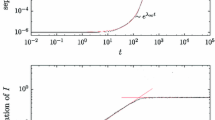
The issue of the high-dimensionality of the system becomes manifest prominently in the low-noise regime, which feature probability distributions displaying very abrupt changes on small spatial scales. In such cases, one must increase L in order to include modes $e^{imy_1}e^{ily_2}$ with higher spatial frequencies $|\varvec{\mathbf {k}}|=\sqrt{m^2+l^2}$ in the expansion of $P_0(\varvec{\mathbf {y}})$ and $\tilde{H}(\varvec{\mathbf {y}};\omega )$. This will limit in practice the applicability of the matrix-inversion method in the weak-noise regime, even if using sparse methods.

Appendix B: Estimating the Parameter $\delta (\alpha )$

Here we show how to calculate the value of $\delta$ from a matching condition.

For our original system Eq. 1 in the absence of noise, i.e. for

$$\begin{aligned} \dot{y}_1= & {} \cos (y_1)\sin (y_2)+\alpha \sin (2y_1), \nonumber \\ \dot{y}_2= & {} -\sin (y_1)\cos (y_2)+\alpha \sin (2y_2) \end{aligned}$$

(B1)

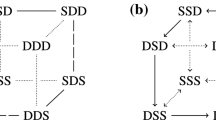
the eigenvalues at the saddle points are $\pm 1-2\alpha$, and the saddles are located at $(\pm \pi /2,\pm \pi /2)$. Consider the saddle located at $(\pi /2,\pi /2)$. The quadrant surrounding this point is the region bordered by the ingress boundary $(y_1=0,0<y_2\le \pi /2)$ and the egress boundary $(0<y_1\le \pi /2,y_2=0)$ (cf. Fig. 10). At this saddle, the stable eigenvector is (1, 0) and the unstable one is (0, 1). The difficulty in estimating the effective value of $\delta$ is that the flow in this square is nonlinear.

Consider the deterministic linearization of the flow around the saddle at $(\pi /2,\pi /2)$ in terms of the variables $u_1$ and $u_2$:

$$\begin{aligned} \dot{u}_1&=(-1-2\alpha )u_1\end{aligned}$$

(B2)

$$\begin{aligned} \dot{u}_2&=(1-2\alpha )u_2. \end{aligned}$$

(B3)

We are interested in matching the properties (namely the first passage time distribution) of the linearized and nonlinear systems when the noise is very small. Thus, we aim to establish an explicit mapping between the deterministic flow of the linearized system and the deterministic flow of the nonlinear system, because for small noise the effect on the trajectories only comes into play close to the fixed point, where the linearization is accurate.

Fig. 10

For illustration, we show simulated trajectories for different noise intensities as indicated. Referring to the saddle point at $(\pi /2,\pi /2)$, the vertical and horizontal blue lines indicate the ingress and egress boundaries, respectively

For the linearized system the ingress boundary is given by $u_1=\delta ,0\le u_2<\delta$. In order to determine $\delta$ we use the matching properties of the flows. In particular, we consider the flow along an invariant subset, namely the solution

$$\begin{aligned} u_1(t)=\delta e^{(-1-2\alpha )t},\quad u_2(t)=0 \end{aligned}$$

(B4)

which corresponds to the solution of the initial value problem starting from the ingress boundary

$$\begin{aligned} y_1(0)=0,\quad y_2(0)=\pi /2. \end{aligned}$$

(B5)

Thus we wish to solve the initial value problem

$$\begin{aligned} \dot{y}=\cos (y)+\alpha \sin (2y),\quad y(0)=0, \end{aligned}$$

(B6)

and choose $\delta$ so that the linearized flow matches as the trajectories approach the saddle point. That is, we wish to choose $\delta$ so that

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{\frac{\pi }{2}-y(t)}{\delta e^{(-1-2\alpha )t}}=1. \end{aligned}$$

(B7)

Or, equivalently, we set

$$\begin{aligned} \delta =\lim _{t\rightarrow \infty }\left[ e^{(1+2\alpha )t}\left( \frac{\pi }{2}-y(t)\right) \right] . \end{aligned}$$

(B8)

We can simplify this as follows: We use the relation $y_1(t)=\text{ arcsin }(z_1(t))$ and the implicit solution for $z_1(t)$, Eq. 49 in the asymptotic limit $t\rightarrow \infty$. In this limit, $z_1$ is very close to 1 and the time variable $t(z_1)$ is dominated by the logarithm $\ln (1-z_1)$. For a more precise approximation of Eq. 49 in the asymptotic limit, we can set $z_1=1$ in the other two logarithmic terms

$$\begin{aligned} t(z_1)=\frac{\ln (2)}{2-4\alpha }-\frac{2\alpha \ln (1+2\alpha )}{1-4\alpha ^2}-\frac{\ln (1-z_1)}{2+4\alpha }=t_s-\frac{\ln (1-z_1)}{2+4\alpha }, \end{aligned}$$

(B9)

where $t_s$ is the constant defined by the first two terms. This equation can be quickly solved for $z_1$:

$$\begin{aligned} z_1(t)=1-\exp \left[ -(2+4\alpha )(t-t_s)\right] ,\qquad t\rightarrow \infty \end{aligned}$$

(B10)

Making use of the series expansion

$$\begin{aligned} \text{ arcsin }(1-\varepsilon )\approx \frac{\pi }{2}-\sqrt{2\varepsilon },\qquad \varepsilon \ll 1 \end{aligned}$$

(B11)

we find exactly the inverse of the diverging prefactor and the finite limit for $\delta$:

$$\begin{aligned} \delta =\lim \limits _{t\rightarrow \infty } e^{(1+2\alpha )t}\sqrt{2} e^{-(1+2\alpha )(t-t_s)}=\sqrt{2} \exp \left[ (1+2\alpha )t_s\right] , \end{aligned}$$

(B12)

which can be further simplified by Eq. B9, yielding Eq. 18.