Langevin Picture of Lévy Walks and Their Extensions

Abstract

In this paper we derive Langevin picture of Lévy walks. Applying recent advances in the theory of coupled continuous time random walks we find a limiting process of the properly scaled Lévy walk. Next, we introduce extensions of Levy walks, in which jump sizes are some functions of waiting times. We prove that under proper scaling conditions, such generalized Lévy walks converge in distribution to the appropriate limiting processes. We also derive the corresponding fractional diffusion equations and investigate behavior of the mean square displacements of the limiting processes, showing that different coupling functions lead to various types of anomalous diffusion.

Appendices

Appendix A

Proof of Theorem 1

In the proofs below we use the following notation: X(⋅) denotes stochastic process X while X(t) is its one-dimensional distribution. Similarly $X_{n}(\cdot) \stackrel{d}{\longrightarrow} X(\cdot)$ means the functional convergence in distribution in the J ₁ Skorokhod topology (see [5]) and $X_{n}(t) \stackrel {d}{\longrightarrow} X(t)$ denotes convergence of one-dimensional distributions. Moreover f∘g is the composition of functions f and g.

We show convergence $R(n\cdot)/n \stackrel{d}{\longrightarrow }(L_{\alpha}^{-} \circ S_{\alpha}^{-1})^{+}(\cdot)$ applying recently developed technique of proving a weak convergence of sequences of coupled CTRWs. Below we briefly present this method.

Consider an array {(J _n,i ,T _n,i )} _n,i≥1 of random vectors in ℝ×[0,∞). We allow that elements of each vector (J _n,i ,T _n,i ) may be dependent. This array generates sequence of coupled CTRWs defined as follows

Additionally we define sequences of processes of partial sums

$$Z_n(\cdot) = \sum_{i=1}^{[n\cdot]}J_{n,i} \quad \mbox{and} \quad W_n(\cdot) = \sum _{i=1}^{[n\cdot]} T_{n,i}.$$

Proposition 1

(See Th. 3.6 [53])

Assume joint convergence $(Z_{n}(\cdot), W_{n}(\cdot)) \stackrel {d}{\longrightarrow} (Z(\cdot), W(\cdot))$ where process W has strictly increasing trajectories. Then

$$R_n(\cdot) \stackrel{d}{\longrightarrow} \bigl(Z^- \circ \bigl(W^{-1}\bigr)^-\bigr)^+(\cdot).$$

The proof has the following structure. First we specify the array {(J _n,i ,T _n,i )} in such way that auxiliary sequence of CTRWs R _n (⋅) generated by this array is related to the sequence of scaled Lévy walks R(n⋅)/n. Then we show joint convergence $(Z_{n}(\cdot), W_{n}(\cdot)) \stackrel{d}{\longrightarrow} (L_{\alpha}(\cdot), S_{\alpha}(\cdot))$. Finally we use Proposition 1 to prove convergence $R(n\cdot)/n\stackrel{d}{\longrightarrow}(L_{\alpha}^{-} \circ S_{\alpha}^{-1})^{+}(\cdot)$.

We define array {(J _n,i ,T _n,i )} _n,i≥1={(n ^−1/α I _i T _i , n ^−1/α T _i )} _n,i≥1. Auxiliary sequence of CTRWs generated by this array has the form

$$R_n(\cdot) = n^{-1/\alpha} \sum_{i=1}^{N_n(\cdot)}I_i T_i$$

where

Observe that

This allows us to find relation between sequences R(n⋅)/n and R _n (⋅), namely

$$\frac{R(n\cdot)}{n} = \frac{1}{n} \sum_{i=1}^{N(n\cdot)}I_i T_i = \bigl(n^\alpha\bigr)^{-1/\alpha}\sum_{i=1}^{N_{n^\alpha}(\cdot)} I_iT_i = R_{n^\alpha}(\cdot).$$

Therefore sequences R(n⋅)/n and R _n (⋅) have the same limiting process.

Now we show joint convergence $(Z_{n}(\cdot), W_{n}(\cdot)) \stackrel {d}{\longrightarrow} (L_{\alpha}(\cdot), S_{\alpha}(\cdot))$, where

$$Z_n(\cdot) = \sum_{i=1}^{[n\cdot]}J_{n,i} = n^{-1/\alpha} \sum_{i=1}^{[n\cdot]}I_i T_i \quad\mbox{and} \quad W_n(\cdot) =\sum_{i=1}^{[n\cdot]} T_{n,i} =n^{-1/\alpha} \sum_{i=1}^{[n\cdot]}T_i$$

are the sequences of partial sum processes given by the array {(J _n,i ,T _n,i )} _n,i≥1.

Let be a process counting positive jumps.

Waiting times {T _i } is the IID sequence, thus for any t>0 we may write

(24)

where $\stackrel{d}{=}$ denotes equality of distributions and sequences {T _i,1} and {T _i,2} are the independent copies of sequence {T _i }. We define sequences of new processes

$$W_{n,1} (\cdot) = n^{-1/\alpha} \sum_{i=1}^{[n\cdot]}T_{i,1}, \qquad W_{n,2}(\cdot) = n^{-1/\alpha} \sum _{i=1}^{[n\cdot]} T_{i,2}.$$

Note that, these processes are independent copies of W _n (⋅), thus from assumption (3) meaning that $W_{n}(\cdot)\stackrel{d}{\longrightarrow} S_{\alpha}(\cdot)$, it follows that $W_{n,1}(\cdot) \stackrel{d}{\longrightarrow} S_{\alpha}^{(1)}(\cdot )$ and $W_{n,2}(\cdot) \stackrel{d}{\longrightarrow} S_{\alpha}^{(2)}(\cdot)$ and $S_{\alpha}^{(1)}(\cdot)$, $S_{\alpha}^{(2)}(\cdot )$ are independent copies of S _α (⋅).

We use the above processes to construct processes

$$X_n(\cdot) = W_{n,1} \biggl(\frac{C(n\cdot)}{n} \biggr) -W_{n,2} \biggl(\frac{[n\cdot] - C(n\cdot)}{n} \biggr)$$

and

$$T_n(\cdot) = W_{n,1} \biggl(\frac{C(n\cdot)}{n} \biggr) +W_{n,2} \biggl(\frac{[n\cdot] - C(n\cdot)}{n} \biggr).$$

Then equality (24) takes form

$$\bigl(Z_n(t), W_n(t) \bigr) \stackrel{d}{=}\bigl(X_n(t), T_n(t) \bigr).$$

One can easily check that processes (Z _n (⋅),W _n (⋅)) and ((X _n (⋅),T _n (⋅)) have the same finite-dimensional distributions. We show only equality of two-dimensional distributions, since the technique of proof carries over to higher dimensions. Take t ₁<t ₂. Then

It is well known that C(n⋅)/n→pe(⋅) almost surely, where e(t)=t is the identity function. J ₁-continuity of composition (Th. 13.2.2 [60]) together with Th. 5.5 [5] yield that

$$W_{n,1} \biggl(\frac{C(n\cdot)}{n} \biggr) \stackrel {d}{\longrightarrow} S_\alpha^{(1)}(p\cdot) \quad \mbox{and} \quad W_{n,2} \biggl(\frac{[n\cdot] - C(n\cdot)}{n} \biggr) \stackrel {d}{\longrightarrow} S_\alpha^{(2)} \bigl((1-p)\cdot \bigr).$$

Since $S_{\alpha}^{(1)}(\cdot)$ and $S_{\alpha}^{(2)}(\cdot)$ are independent, they have no common jumps almost surely. Then we apply theorem on J ₁-continuity of addition (Th. 4.1 [61]) together with Th. 5.5 [5] and next using self-similarity property of stable processes $S_{\alpha}^{(1)}(\cdot)$, $S_{\alpha}^{(2)}(\cdot)$ we obtain

Processes (Z _n (⋅),W _n (⋅)) and (X _n (⋅),T _n (⋅)) have the same distributions, thus

$$ \bigl(Z_n(\cdot), W_n(\cdot)\bigr) \stackrel{d}{\longrightarrow} \bigl(L_\alpha (\cdot),S_\alpha(\cdot)\bigr)$$

(25)

where $(L_{\alpha}(\cdot), S_{\alpha}(\cdot)) \stackrel{d}{=} (X(\cdot ), T(\cdot))$. It is straightforward to check that L _α (⋅) and S _α (⋅) have Fourier transforms of the form (8) and (4). Using Th. 7.3.5 and Corr. 7.3.4 [41] from formula (4) we derive Lévy measure of process S _α (⋅)

$$\nu_{S_\alpha}(dx) = \frac{\alpha}{\varGamma(1 - \alpha)}x^{-\alpha-1}dx.$$

Moreover, observe that we can decompose process (L _α (⋅),S _α (⋅)) in the following way

$$\bigl(L_\alpha(\cdot), S_\alpha(\cdot)\bigr) \stackrel{d}{=}p^{1/\alpha } \bigl(S_\alpha^{(1)}(\cdot),S_\alpha^{(1)}(\cdot) \bigr) + (1-p)^{1/\alpha}\bigl(-S_\alpha^{(2)}(\cdot), S_\alpha^{(2)}(\cdot ) \bigr),$$

where $S_{\alpha}^{(1)}(\cdot)$ and $S_{\alpha}^{(2)}(\cdot)$ are independent copies of S _α (⋅). Thus processes $(S_{\alpha}^{(1)}(\cdot), S_{\alpha}^{(1)}(\cdot) )$ and $(-S_{\alpha}^{(2)}(\cdot), S_{\alpha}^{(2)}(\cdot) )$ are mutually independent and it is easy to see that their Lévy measures are of the form

$$\nu_{(S_\alpha^{(1)}(\cdot), S_\alpha^{(1)}(\cdot))}(dx_1 \times dx_2) =\delta_{x_2}(dx_1) \nu_{S_\alpha}(dx_2)$$

and

$$\nu_{(-S_\alpha^{(2)}(\cdot), S_\alpha^{(2)}(\cdot))}(dx_1 \times dx_2) =\delta_{-x_2}(dx_1) \nu_{S_\alpha}(dx_2).$$

Next, using a well known fact that sum of independent Lévy processes is again a Lévy process and Lévy measure of this sum is equal to the sum of Lévy measures of summands together with self-similarity property of stable processes we obtain that

$$\nu_{(L_\alpha, S_\alpha)}(dx_1 \times dx_2) = p\delta_{x_2}(dx_1) \nu_{S_\alpha}(dx_2) +(1-p) \delta_{-x_2}(dx_1) \nu_{S_\alpha}(dx_2).$$

Finally, by Proposition 1 we have that

$$R_n(\cdot) \stackrel{d}{\longrightarrow} \bigl(L_\alpha^-\circ \bigl(S_\alpha^{-1}\bigr)^- \bigr)^+(\cdot).$$

Since S _α (⋅) is a strictly increasing α-stable subordinator it follows that $S_{\alpha}^{-1}(\cdot)$ is continuous and $(S_{\alpha}^{-1})^{-}(\cdot)= S_{\alpha}^{-1}(\cdot)$. Moreover, as we have shown, sequences R(n⋅)/n and R _n (⋅) have the same limiting process, thus

$$\frac{R(n\cdot)}{n} \stackrel{d}{\longrightarrow} \bigl(L_\alpha^- \circ \bigl(S_\alpha^{-1}\bigr) \bigr)^+(\cdot)$$

which completes the proof. □

Appendix B

Proof of Theorem 2

We use similar method as in proof of Theorem 1. We take the array $\{(J_{n,i}, T_{n,i})\}_{n,i \geq1} \stackrel{\mathrm{def}}{=} \{(n^{-\gamma /\alpha} I_{i} T_{i}^{\gamma}, n^{-1/\alpha}T_{i})\}_{n,i \geq1}$ and the auxiliary sequence of CTRWs

$$R_n(\cdot) = \sum_{i=1}^{N_n(\cdot)}T_{n,i} = n^{-\gamma/\alpha} \sum_{i=1}^{N_n(\cdot)}I_i T_i^\gamma $$

where

Using equality $N(n\cdot)= N_{n^{\alpha}}(\cdot)$ we obtain that

$$\frac{R(n\cdot)}{n^\gamma} = \frac{1}{n^\gamma} \sum_{i=1}^{N(n\cdot)}I_i T_i^\gamma= \bigl(n^\alpha \bigr)^{-\gamma/\alpha} \sum_{i=1}^{N_{n^\alpha}(\cdot)}I_i T_i^\gamma= R_{n^\alpha }(\cdot),$$

thus sequences R(n⋅)/n ^γ and R _n (⋅) have the same limiting process.

Next we investigate converge of the sequences of processes of partial sums given by the array {(J _n,i ,T _n,i )} defined below

$$Z_n(\cdot) \stackrel{\mathrm{def}}{=} \sum_{i=1}^{[n\cdot]}J_{n,i}= n^{-\gamma/\alpha} \sum_{i=1}^{[n\cdot]}I_iT_i^\gamma \quad\mbox {and} \quad W_n(\cdot)\stackrel{\mathrm{def}}{=} \sum_{i=1}^{[n\cdot ]}T_{n,i}= n^{-1/\alpha} \sum_{i=1}^{[n\cdot]}T_i.$$

Convergence $W_{n}(\cdot) \stackrel{d}{\longrightarrow} S_{\alpha}(\cdot)$ is assumed (see (3)), so convergence $W_{n}(1) \stackrel{d}{\longrightarrow} S_{\alpha}(1)$ holds as well. It was shown in Appendix A that Lévy measure of process S _α is of the form

$$\nu_{S_\alpha} (dx ) = C_{S_\alpha} x^{-\alpha- 1}dx ,\quad \mbox{where } C_{S_\alpha} = \frac{\alpha}{\varGamma(1 -\alpha)}.$$

Theorem 3.2.2 [41] implies then that the array {T _n,i }={n ^−1/α T _i } satisfies the following conditions:

• (a) $nP(n^{-1/\alpha} T_{1} > x) \longrightarrow C_{S_{\alpha}}x^{-\alpha}$, x>0;

• (b) For all t∈ℝ $Q_{S_{\alpha}}(t) = 0$ where

  

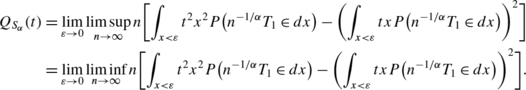
We show that similar conditions hold for the array $\{J_{n,i}\} = \{n^{-\gamma/\alpha} I_{i} T_{i}^{\gamma}\}$. Observe that for x>0

Similarly

$$nP\bigl(n^{-\gamma/\alpha} I_i T_i^\gamma< - x\bigr) \longrightarrow\frac {1}{2} C_{S_\alpha} x^{-\alpha/\gamma}.$$

Therefore the array {J _n,i } satisfies condition (a) of Th. 3.2.2 [41]. Define

Distribution of $n^{-\gamma/\alpha} I_{i} T_{i}^{\gamma}$ is symmetric hence

$$\int_{|x|<\varepsilon} t x P\bigl(n^{-\gamma/\alpha} I_iT_i^\gamma \in dx\bigr) = 0.$$

Observe that

For any a<ε we have that

Thus

$$\lim_{n \to\infty} n\int_0^\varepsilon x^2 P\bigl(n^{-\gamma/\alpha} T_i^\gamma\in dx\bigr) \leq C_{S_\alpha} \frac{\alpha/\gamma}{2-\alpha /\gamma} \varepsilon^{2-\alpha/\gamma}$$

and

$$\lim_{n \to\infty} n\int_{|x|<\varepsilon} x^2 P\bigl(n^{-\gamma /\alpha} I_i T_i^\gamma\in dx\bigr) \leq C_{S_\alpha} \frac{\alpha /\gamma}{2-\alpha/\gamma} \varepsilon^{2-\alpha/\gamma}\to 0 \quad \mbox{as } \varepsilon\to0.$$

As the conclusion from observations above we have that the array $\{J_{n,i}\} = \{n^{-\gamma/\alpha} I_{i} T_{i}^{\gamma}\}$ fulfills condition (b) of Th. 3.2.2 [41] with $Q_{L_{\alpha/\gamma}}(t) =0$ and by this theorem we have that

$$Z_n(1) \stackrel{d}{\longrightarrow} L_{\alpha/\gamma}.$$

Moreover from Th. 7.3.5 [41] it follows that random variable L _α/γ has the characteristic function given by (18) with t=1. In order to complete proof of convergence $Z_{n}(\cdot)\stackrel {d}{\longrightarrow} L_{\alpha/\gamma}(\cdot)$ we use the following proposition

Proposition 2

(Invariance principle for Lévy processes; see e.g. [46] p. 197)

Let {ζ _n,i } _n,i≥1 be an array of random variables such that in each row ζ _n,i are IID and

$$\xi_n \stackrel{\mathrm{def}}{=} \sum_{i=1}^{n}\zeta_{n,i} \stackrel {d}{\longrightarrow} \xi $$

where ξ is some infinitely divisible random variable. Then convergence of processes

$$\xi_n(\cdot) \stackrel{\mathrm{def}}{=} \sum_{i=1}^{[n\cdot]}\zeta_{n,i} \stackrel{d}{\longrightarrow} \xi(\cdot)$$

also holds with ξ(⋅) being a Lévy process such that $\xi (1) \stackrel{d}{=} \xi$. This principle easily carries over to higher dimensions.

As a conclusion from the above proposition we obtain that

$$Z_n(\cdot) \stackrel{d}{\longrightarrow} L_{\alpha/\gamma}(\cdot)$$

where L _α/γ (⋅) is a stable Lévy motion with characteristic function given by (18).

Next we show joint convergence $(Z_{n}(\cdot), W_{n}(\cdot)) \stackrel {d}{\longrightarrow} (L_{\alpha/\gamma}(\cdot), S_{\alpha}(\cdot ))$. Observe that the array $\{(J_{n,i}, T_{n,i})\} = \{(n^{-\gamma /\alpha} I_{i} T_{i}^{\gamma}, n^{-1/\alpha}T_{i})\}$ satisfies condition (a) of Th. 3.2.2 [41]. Namely, for any Borel sets $B_{1} \in \mathcal{B}(\mathbb{R})$ and $B_{2} \in\mathcal{B}([0, \infty))$ such that (0,0)∉B ₁×B ₂ we have that

where (B ₁∩(0,∞))^1/γ={x>0:x ^γ∈B ₁∩(0,∞)} and (−B ₁∩(0,∞))^1/γ={x>0:−x ^γ∈B ₁∩(−∞,0)}.

It is straightforward to check that measure $\nu_{(L_{\alpha/\gamma },S_{\alpha})}$ given by formula

$$ \nu_{(L_{\alpha/\gamma},S_\alpha)}(B_1 \times B_2) = \frac{1}{2} \nu_{S_\alpha}\bigl(B_1^{1/\gamma}\cap B_2\bigr) + \frac{1}{2} \nu_{S_\alpha} \bigl(\bigl(-B_1^{1/\gamma}\bigr) \cap B_2 \bigr)$$

(26)

is indeed a Lévy measure. Equivalently we can write it in the form

$$\nu_{(L_{\alpha/\gamma},S_\alpha)}(dx_1 \times dx_2)=\frac {1}{2}\delta_{x_2^\gamma}(dx_1)\nu_{S_\alpha}(dx_2)+\frac{1}{2}\delta_{-x_2^\gamma}(dx_1)\nu_{S_\alpha}(dx_2).$$

Moreover processes S _α (⋅) and L _α/γ (⋅) do not have Gaussian component, thus condition (b) of Th. 3.2.2 [41] is satisfied with $Q_{(L_{\alpha/\gamma},S_{\alpha})}(t) = 0$. Hence we have joint convergence

$$\bigl(Z_n(1), W_n(1)\bigr) \stackrel{d}{\longrightarrow} \bigl(L_{\alpha/\gamma }(1),S_\alpha(1)\bigr)$$

and by Proposition 2 convergence

$$\bigl(Z_n(\cdot), W_n(\cdot)\bigr) \stackrel{d}{\longrightarrow} \bigl(L_{\alpha /\gamma}(\cdot),S_\alpha(\cdot)\bigr)$$

also holds.

Note that from formula (26) one easily finds that processes S _α (⋅) and L _α/γ (⋅) have simultaneous jumps and the length of each jump of L _α/γ (⋅) is equal to the length of corresponding jump of S _α (⋅) raised to the power γ.

By Proposition 1 in Appendix A we have that auxiliary sequence of CTRWs R _n (⋅) converges to $(L_{\alpha/\gamma }^{-} \circ(S_{\alpha}^{-1})^{-} )^{+}(\cdot)$. Since sequences R(n⋅)/n ^γ and R _n (⋅) have the same limiting process and $S_{\alpha}^{-1}(\cdot)$ is continuous we obtain desired convergence

$$\frac{R(n\cdot)}{n^\gamma} \stackrel{d}{\longrightarrow} \bigl(L_{\alpha/\gamma}^- \circ \bigl(S_\alpha^{-1}\bigr) \bigr)^+(\cdot).$$

 □

Appendix C

Proof of Theorem 3

The technique we use in proof of Theorem 3. is similar to that in proof of Theorem 2. Define array $\{(J_{n,i}, T_{n,i})\}_{n,i \geq1}\stackrel{\mathrm{def}}{=} \{(n^{-1/2} I_{i} \exp(-T_{i}), n^{-1/\alpha}T_{i})\}_{n,i \geq1}$ and the auxiliary sequence of CTRWs

$$R_n(\cdot) = \sum_{i=1}^{N_n(\cdot)}T_{n,i} = n^{-1/2} \sum_{i=1}^{N_n(\cdot)}I_i \exp(-T_i)$$

where

Relation $N(n\cdot)= N_{n^{\alpha}}(\cdot)$ yields

$$\frac{R(n\cdot)}{n^{\alpha/2}} = \frac{1}{n^{\alpha/2}} \sum_{i=1}^{N(n\cdot)}I_i \exp(-T_i) = \bigl(n^\alpha \bigr)^{-1/2} \sum_{i=1}^{N_{n^\alpha}(\cdot)}I_i \exp(-T_i) = R_{n^\alpha}(\cdot),$$

thus sequences R(n⋅)/n and R _n (⋅) converge to the same limiting process.

Next we investigate joint converge of the sequences of processes of partial sums generated by the array {(J _n,i ,T _n,i )}

$$Z_n(\cdot) \stackrel{\mathrm{def}}{=} \sum_{i=1}^{[n\cdot]}J_{n,i}= n^{-1/2} \sum_{i=1}^{[n\cdot]}I_i\exp(-T_i) \quad \mbox{and} \quad W_n(\cdot) \stackrel{\mathrm{def}}{=} \sum_{i=1}^{[n\cdot]}T_{n,i} =n^{-1/\alpha} \sum_{i=1}^{[n\cdot]}T_i.$$

We apply Th. 3.2.2 [41] to show convergence $(Z_{n}(1),W_{n}(1)) \stackrel{d}{\longrightarrow} (B(1), S_{\alpha}(1))$. First we check that condition (a) of this theorem holds. For any Borel sets $B_{1} \in\mathcal{B}(\mathbb{R})$ and $B_{2} \in\mathcal{B}([0,\infty))$ such that (0,0)∉B ₁×B ₂ we have that

Hence

and

$$nP \bigl( \bigl(n^{-1/2} I_i \exp(-T_i),n^{-1/\alpha}T_1\bigr) \in dx_1 \times dx_2 \bigr) \to \delta_0(dx_1)\nu_{S_\alpha}(dx_2)$$

as n→∞, where δ _a denotes a probability measure concentrated at point a. It means that condition (a) holds with joint Lévy measure $\delta_{0}(dx_{1})\nu_{S_{\alpha}}(dx_{2})$.

Next we check the condition (b). Let t=(t ₁,t ₂)∈ℝ², x=(x ₁,x ₂)∈ℝ². Observe that

For arbitrary fixed ε and for all $n > 1/(\varepsilon^{2} -x_{2}^{2})$ we have that

Moreover

$$C_{n, 2} \leq\int_{x_2 < \varepsilon} x_2^2nP\bigl(n^{-1/\alpha}T_1 \in dx_2\bigr) \to \operatorname{const}\cdot\varepsilon^{2-\alpha}.$$

Next observe that

Hence

for some M<∞. The last inequality comes from the fact that

$$\int_{x_2<\varepsilon} x_2 nP\bigl(n^{-1/\alpha}T_1\in dx_2\bigr) \to \operatorname{const} \cdot\varepsilon^{1-\alpha},$$

thus for all n≥1 integrals above are jointly bounded. As n→∞ we have that

$$n \biggl( \int_{\|x\|<\varepsilon} \langle t, x\rangle P \bigl( \bigl(n^{-1/2}I_i \exp (-T_i), n^{-1/\alpha}T_1\bigr)\in dx_1 \times dx_2 \bigr) \biggr)^2 \to0.$$

By the above observations it follows that condition (b) of Th. 3.2.2 [41] holds with

$$Q(t) = t_1^2 \mathbb{E}e^{-2T_1}.$$

Therefore distribution of (Z _n (1),W _n (1)) converges to the infinitely divisible distribution given by characteristic function

$$\phi(t) = \exp \biggl(- \frac{1}{2} t_1^2\mathbb{E}e^{-2T_1} + \int_{\|x\| > 0} \bigl(e^{i t_2 x_2}- 1 \bigr)\nu_{S_\alpha }(dx_2) \biggr).$$

One easily checks that ϕ is the characteristic function of $(\sqrt{\mathbb{E}e^{-2T_{1}}}B(1), S_{\alpha}(1) )$ where B(⋅) is a standard Brownian motion independent of stable subordinator S _α (⋅). By Proposition 2 (see Appendix B) it also follows that

$$\bigl(Z_n(\cdot) , W_n(\cdot)\bigr) \stackrel{d}{\longrightarrow} \bigl(\sqrt{\mathbb{E}e^{-2T_1}}B(\cdot),S_\alpha(\cdot) \bigr).$$

By Proposition 1 in Appendix A, we obtain

$$R_n(\cdot) \stackrel{d}{\longrightarrow} \bigl(\sqrt{\mathbb {E}e^{-2T_1}}B^- \circ\bigl(S_\alpha^{-1}\bigr)^-\bigr)^+(\cdot).$$

Since both B(⋅) and $S_{\alpha}^{-1}(\cdot)$ are continuous and sequence R(n⋅)/n ^α/2 converges to the same limit as R _n (⋅) we finally get

$$\frac{R(n\cdot)}{n^{\alpha/2}} \stackrel{d}{\longrightarrow} \bigl(\sqrt{\mathbb{E}e^{-2T_1}}B \circ\bigl(S_\alpha^{-1}\bigr)\bigr) (\cdot).$$

 □